Экспериментальная оценка коэффициентов сжимаемости трещин  и межзерновых пор коллектора нефти и газа

В. С. Жуков; Ю. О. Кузьмин

doi:10.31897/PMI.2021.5.5

Том 251

Страницы:

658-666

Скачать том:

RUS ENG

Научная статья

Геотехнология и инженерная геология

Экспериментальная оценка коэффициентов сжимаемости трещин и межзерновых пор коллектора нефти и газа

Авторы:

В. С. Жуков¹

Ю. О. Кузьмин²

Об авторах

1 — д-р техн. наук главный научный сотрудник Институт физики Земли им. О.Ю.Шмидта Российской академии наук ▪ Orcid ▪ Elibrary
2 — д-р физ.-мат. наук заместитель директора Институт физики Земли им. О.Ю.Шмидта Российской академии наук ▪ Orcid

Дата отправки:

2021-05-31

Дата принятия:

2021-10-18

Дата публикации:

2021-10-29

Аннотация

Статья посвящена исследованиям объемной реакции горных пород, вызванной изменениями их напряженного состояния. Экспериментально получены и проанализированы изменения объема трещинной и межзерновой компонент порового пространства на основе измерений объема поровой жидкости, выдавливаемой из образца горной породы при увеличении его всестороннего обжатия. Определение трещинной и межзерновой компонент пористости основано на ранее предложенном авторами способе их расчета по величинам скорости продольной волны и общей пористости. Рассмотрены результаты экспериментальных и аналитических исследований изменений пористости и двух ее компонент (межзерновой и трещинной) при воздействии эффективных напряжений. Этот подход позволил авторам оценить величину диапазона изменений объемной сжимаемости как межзерновых пор, так и трещин на представительной коллекции из 37 образцов песчаного коллектора вендского возраста Чаяндинского месторождения. Предложен метод раздельной оценки коэффициентов сжимаемости трещин и межзерновых пор, экспериментально получены их значения и зависимости от эффективного давления . Определено, что знание величин коэффициентов объемной сжимаемости трещинной и межзерновой пористости повысит достоверность оценок изменений петрофизических параметров коллекторов нефти и газа, обусловленных изменениями напряженного состояния в процессе разработки месторождений углеводородов.

Ключевые слова:

горная порода пористость сжимаемость горных пород сжимаемость пор межзерновая пористость трещинная пористость сжимаемость трещин разработка месторождений углеводородов

10.31897/PMI.2021.5.5

Введение

Разработка месторождений нефти, газа и твердых полезных ископаемых требует учета упругой объемной реакции горных пород, вызванной изменениями их напряженного состояния [28, 34, 43]. Вследствие сложной структуры порового пространства горных пород, состоящей из межзерновых пор и трещин [2, 4], изменение объема каждой из компонент требует самостоятельного рассмотрения и анализа [5, 6]. Актуальной задачей является анализ и оценка величины деформации межзерновых пор и трещин, которые возникают из-за изменения напряженного состояния коллектора, вызванного добычей углеводородов [5, 11, 23]. Так, в работе [19] отмечена необходимость учета зависимости фильтрационно-емкостных свойств коллекторов порового и трещинного типа от изменений напряженного состояния в процессе разработки месторождений нефти и газа. «Сжимаемость трещин может отличаться от сжимаемости матрицы на порядок. Так, в коллекторах с естественной трещиноватостью на месторождениях Киркук (Ирак) и Асмари (Иран) сжимаемость трещин варьирует в диапазоне 6-60 ГПа^–1. На Грозненском месторождении сжимаемость трещин изменяется от 10 до 100 ГПа^–1. На всех этих месторождениях сжимаемость трещин в 10-100 раз больше, чем сжимаемость межзерновой матрицы, и принимать, что они равны – неприемлемая практика» [38].

Теория вопроса

Коэффициент объемной сжимаемости – это параметр, количественно определяющий зависимость между давлением, оказываемым на тело, и результирующим изменением его объема. Материал без пор и трещин имеет единственную сжимаемость, определяемую формулой:

C = \frac{- 1}{V_{0}} \frac{d V}{d P}, (1)

где V₀ – объем тела при начальном давлении; P – гидростатическое давление, оказываемое на его внешнюю поверхность.

Существуют два независимых объема (образца и пор) и два давления (всестороннего сжатия и порового флюида), которые можно варьировать; четыре различные сжимаемости могут быть связаны с пористой породой [40, 41]. В каждой из этих сжимаемых пористых пород изменения либо объема пор V_p, либо объема образца горной породы V_b связаны с изменениями порового давления P_p или всестороннего давления P_с. При их описании используются обозначения, в которых первый индекс указывает на соответствующее изменение объема, а второй – на изменяющееся давление. Эти коэффициенты сжимаемости наиболее четко определены в работе [42]:

сжимаемость объема породы при изменении всестороннего давления

C_{b c} = \frac{- 1}{V_{b 0}} {(\frac{d V_{b}}{d P_{c}})}_{P_{p}}; (2)

сжимаемость объема породы при изменении порового давления

C_{b p} = \frac{1}{V_{b 0}} {(\frac{d V_{b}}{d P_{p}})}_{P_{c}}; (3)

сжимаемость объема пор при изменении всестороннего давления

C_{p c} = \frac{- 1}{V_{p 0}} {(\frac{d V_{p}}{d P_{c}})}_{P_{p}}; (4)

сжимаемость объема пор при изменении порового давления

C_{p p} = \frac{1}{V_{p 0}} {(\frac{d V_{p}}{d P_{p}})}_{P_{c}} . (5)

Также необходимо осветить понятие эффективного давления

P_{эф} = P_{c} - a P_{p}, (6)

где Р_с – давление всестороннего сжатия; Р_р – давление порового (пластового) флюида (вода, нефть, газ); a – коэффициент Биота (иногда называют коэффициентом разгрузки) характеризует ту часть порового давления, которая противодействует всестороннему давлению.

Для горных пород с пористостью более 5 % a зачастую принимается равным единице. В этом случае C_pc и C_pp равны друг другу. Иначе говоря, одинаковые изменения всестороннего и порового давлений изменяют объем порового пространства на одинаковую величину, но противоположную по знаку: увеличение всестороннего сжатия и уменьшение порового давления приводят к уменьшению объема порового пространства.

Для учета упругой энергии всего образца (пласта, залежи) должна учитываться упругость и скелета породы (твердой матрицы), и всех пластовых флюидов. В таком случае термин «полная сжимаемость» [34] или сжимаемость объема породы (образца), следует использовать для представления упругости всей залежи:

C_{t} = \frac{- 1}{V_{b 0}} (\frac{d V_{b}}{d P_{эф}}) . (7)

В общем виде при наличии трех фаз (нефти, воды и газа), одновременно присутствующих в пласте, математическое выражение связи между ними и общей сжимаемости объема породы имеет такой вид [34]:

С_{t} = (C_{o i l} S_{o i l} + C_{g a s} S_{g a s} + C_{w a t e r} S_{w a t e r}) m + C_{s k}, (8)

где C_oil, C_gas, C_water и C_sk – сжимаемость нефти, газа, воды и твердой матрицы (скелета) породы соответственно; m – пористость горной породы; S_oil, S_gas, S_water – содержание (насыщенность) нефти, газа, воды в поровом пространстве горной породы соответственно.

При проведении петрофизических исследований давление и температура порового флюида (модель пластовой воды) поддерживались на одном уровне в 13 МПа и 20 °С, увеличивалось (с 15 до 50 МПа) только всестороннее давление. Поэтому учитывать коэффициент сжимаемости флюида C_water (воды) не требуется.

Величина коэффициента сжимаемости твердой матрицы породы может быть экспериментально определена с помощью так называемых unjacketed tests [34, 42]. В этих испытаниях горная порода находится под давлением флюида (жидкости), который проникает в поры горной породы, вследствие чего всестороннее давление и давление поровой жидкости одинаковы. Но, к сожалению, используемая установка не позволила провести такого рода испытания, и коэффициент сжимаемости минеральной матрицы породы был рассчитан динамическим способом, исходя из скорости распространения упругих волн и плотности горных пород:

C_{s k} = \frac{3}{2} [(\frac{1}{v_{p}^{2}}) (\frac{1}{v_{s}^{2}})] / [δ(1 +μ ) (\frac{1}{v_{s}^{2}} – \frac{1}{v_{p}^{2}})], (9)

где C_sk – коэффициент сжимаемости минеральной матрицы (скелета), ГПа^–1; v_p – скорость продольной волны, км/с; v_s – скорость поперечной волны, км/с; δ – плотность, г/см³; μ – коэффициент Пуассона (динамический).

Сжимаемости C_pcи C_pp являются сжимаемостями пор и выражают влияние изменений давления на объем пустотного пространства, содержащегося в породе. Сжимаемость пор C_pp используется при анализе пластового резервуара, поскольку она отражает объем избыточной поровой жидкости, которая может храниться в поровом пространстве из-за увеличения давления пор. Эта сжимаемость добавляется к сжимаемости пластового флюида C_f для того, чтобы представить их сумму как сжимаемость пласта, которая используется в основном уравнении пласта. В этом случае предполагается, что поровое и всестороннее давления являются независимыми переменными; физически это соответствует так называемому дренированному сжатию (открытая система пор), при котором изменения всестороннего давления не вызывают изменения порового давления. Закрытая система пор приводит к недренированному сжатию при повышении всестороннего сжатия, однако, как правило, не является коллектором, поскольку из этих пор невозможно извлечь флюид без дополнительного воздействия с целью создания дополнительных каналов фильтрации.

Изменения объемной деформации образца и объемной деформации пор могут быть выражены в терминах сжимаемости пористой породы:

\begin{array}{l} d ε_{b} = - C_{b c} d P_{c} + C_{b p} d P_{p}; (10) \\ d ε_{p} = - C_{p c} d P_{c} + C_{p p} d P_{p} . (11) \end{array}

Поскольку насыщенный жидкостью песчаник может рассматриваться как гомогенный материал, C_bc – его эффективная объемная сжимаемость как аналог сжимаемости непористого материала. Другая объемная сжимаемость C_b_p, которая была названа псевдообъемной [25], отражает влияние порового давления на полный объем образца горной породы [17]. Эта сжимаемость полезна в расчетах оседания земной поверхности или дна моря при разработке месторождений углеводородов [12, 20, 25].

Когда поровый флюид (нефть, вода, газ) выводится из пласта (подземных залежей), то давление флюида в порах снижается, и общий занимаемый объем залежи (пласта) уменьшается в соответствии с уравнением (7). Последующее оседание поверхности земли над залежью может равняться десяткам метров. Оседания наносят значительный ущерб зданиям и другим сооружениям. Известные примеры оседания нефтяных месторождений – Уилмингтон Лонг Бич в Южной Калифорнии [29] и Экофиск в Северном море [26, 27].

Методика исследования

Экспериментальные исследования проводились в условиях роста только всестороннего сжатия, в отличие от методики ARMA-14-7532 [24], которая предусматривает и дополнительное одноосное сжатие. Использованная методика позволила при увеличении всестороннего обжатия образца измерить объем поровой жидкости, выдавливаемой из образца, и рассчитать не только изменения пористости, но и оценить объемную деформацию. Она рассчитывалась с учетом того, что коэффициент сжимаемости твердой матрицы горной породы на несколько порядков превосходит коэффициент сжимаемости порового пространства.

Пористость в условиях, моделирующих пластовые условия, определялась (с учетом объема жидкости, вытесненной из порового пространства образца горной породы) по формуле:

$$ \mathrm{m=m_{атм}}-ΔVp/V, \qquad(12) $$

где m_атм – коэффициент пористости в атмосферных условиях, %; ΔV_p – объем поровой жидкости, выдавливаемой из образца (изменение объема пор), см³; V – начальный объем образца, см³.

Объемная деформация образца с учетом того, что сжимаемость минерального скелета на два порядка меньше сжимаемости жидкости, рассчитывалась по формуле:

$$ \mathrm{cε}=100ΔVp/V\qquad (13) $$

Коэффициент объемной сжимаемости горной породы определялся по формуле:

C_{b c} = C_{t} = (\frac{Δ V_{p}}{V}) / Δ P_{эф}, (14)

где ΔP_эф – изменения эффективного давления, ГПа.

Для удобства работы с отрицательными числами коэффициентов сжимаемости будем считать положительным уменьшение объема, что равносильно умножению на –1 выражений (1), (2) и (4), в которых положительным принято увеличение объема.

Коэффициент сжимаемости порового пространства определялся по формуле:

C_{p c} = (\frac{Δ V_{p}}{V_{p}}) / Δ P_{эф} . (15)

Поскольку m = V_p/V, то, как отмечено в работе [34], C_t= C_pcm.Таким образом, исходя из формул (4) и (5), были определены коэффициенты объемной сжимаемости горной породы (14) и объемной сжимаемости порового пространства (общей пористости) (15) при изменении эффективного давления.

Результаты

Были исследованы 34 песчано-глинистых образца вендского возраста, имевшие в атмосферных условиях коэффициент пористости 3-15,6 %, коэффициент проницаемости 2-100 мД, изготовленные из керна, поднятого с глубины 1660-1860 м. Образцы представлены в основном крупно- мелкозернистыми песчаниками кварцевого и кварц-полевошпатового состава со смешанным кварц-регенерационным, сульфатным, глинисто-пленочным и частично базальным цементом.

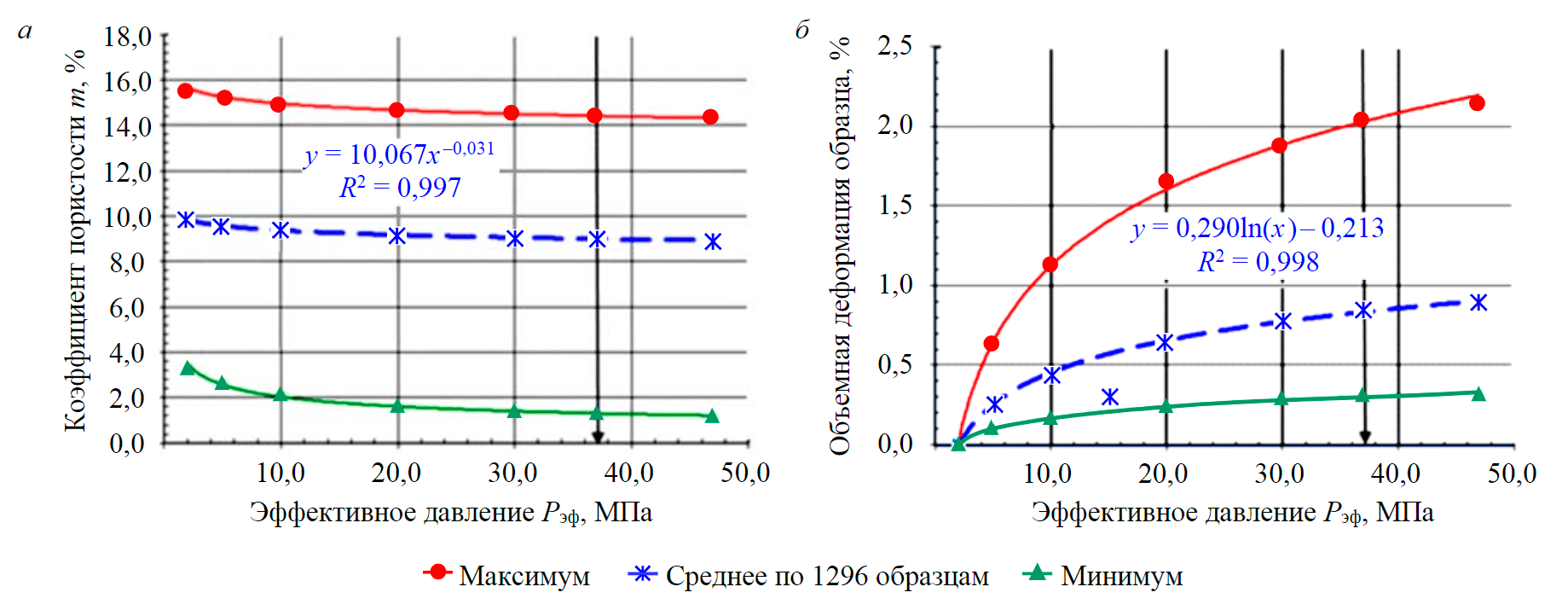
Рис.1. Изменения коэффициента пористости (а) и объемной деформации образцов (б) от эффективного давления

Величины коэффициента пористости образцов горных пород (рис.1, а) Чаяндинского нефтегазоконденсатного месторождения (ЧНГКМ) и объемной деформации образцов горных пород (рис.1, б), полученные при текущих значениях P_эф, позволили получить их зависимости от роста эффективного давления в пласте подобно тому, как показано в работах [1, 8, 23]. Причем изменения объемной деформации образцов соответствуют изменениям пористости, обусловленным ростом P_эф.

Общеизвестно, что поровое пространство образцов горных пород состоит из двух компонент: межзерновой и трещинной. Трещинная пористость выражается как отношение объема трещин к полному объемупороды:

m_{тр} = 100 V_{тр} / V . (16)

Межзерновая пористостьвыражается как отношение объема межзернового пространства к полному объему породы:

m_{мз} = 100 V_{мз} / V . (17)

Ранее был предложен способ определения величины этих компонент, основанный на измерении величины скорости распространения упругой продольной волны [7, 18, 22]. Общая пористость и скорость продольной волны определялись на каждой ступени P_эф. При увеличении всестороннего давления неизменным оставалось давление поровой жидкости и, следовательно, увеличивалосьP_эф. Сжимаемости межзерной и трещинной пористостей и коэффициенты объемной сжимаемости породы (14), межзерновой (16) и трещинной (17) пористостей, определяли с помощью выражений:

\begin{array}{l} C_{мз} = (Δ V_{мз} / V_{мз}) / Δ P_{эф}; (18) \\ C_{тр} = (Δ V_{тр} / V_{тp}) / Δ P_{эф}; (19) \end{array}

где ΔV_мз и ΔV_тр – изменения объема межзернового пространства и трещинной пустотности, соответственно.

Данная методика позволила экспериментально оценить трещинную и межзерновую пористости с ростом P_эф и рассчитать отдельно коэффициенты сжимаемости объема образцов, минеральной матрицы, трещин, межзерновой пористости образцов горных пород в процессе увеличения P_эф при моделировании процесса разработки месторождений углеводородов (таблица).

Средние значения пористости и объемной сжимаемости при различных величинах эффективного давления

Коэффициенты	Эффективное давление Р_эф, МПа
Коэффициенты	2,0	5,0	10,0	20,0	30,0	37,0
Пористости:
общей m, %	9,926	9,681	9,505	9,302	9,163	9,088
межзерновой m_мз, %	9,178	9,025	8,912	8,783	8,694	8,657
трещинной m_тр, %	0,749	0,656	0,593	0,519	0,468	0,432
Сжимаемости:
минерального скелета (динамический, C_sk), ГПа^–1	0,036	0,033	0,032	0,030	0,030	0,029
горной породы С_bc, ГПа^–1		0,491	0,422	0,312	0,255	0,227
порового пространства C_pc, ГПа^–1		5,656	4,705	3,451	2,814	2,501
межзерновых пор C_мз, ГПа^–1		3,484	3,009	2,241	1,798	1,563
трещин С_тр, ГПа^–1		25,35	21,30	15,62	12,64	11,62

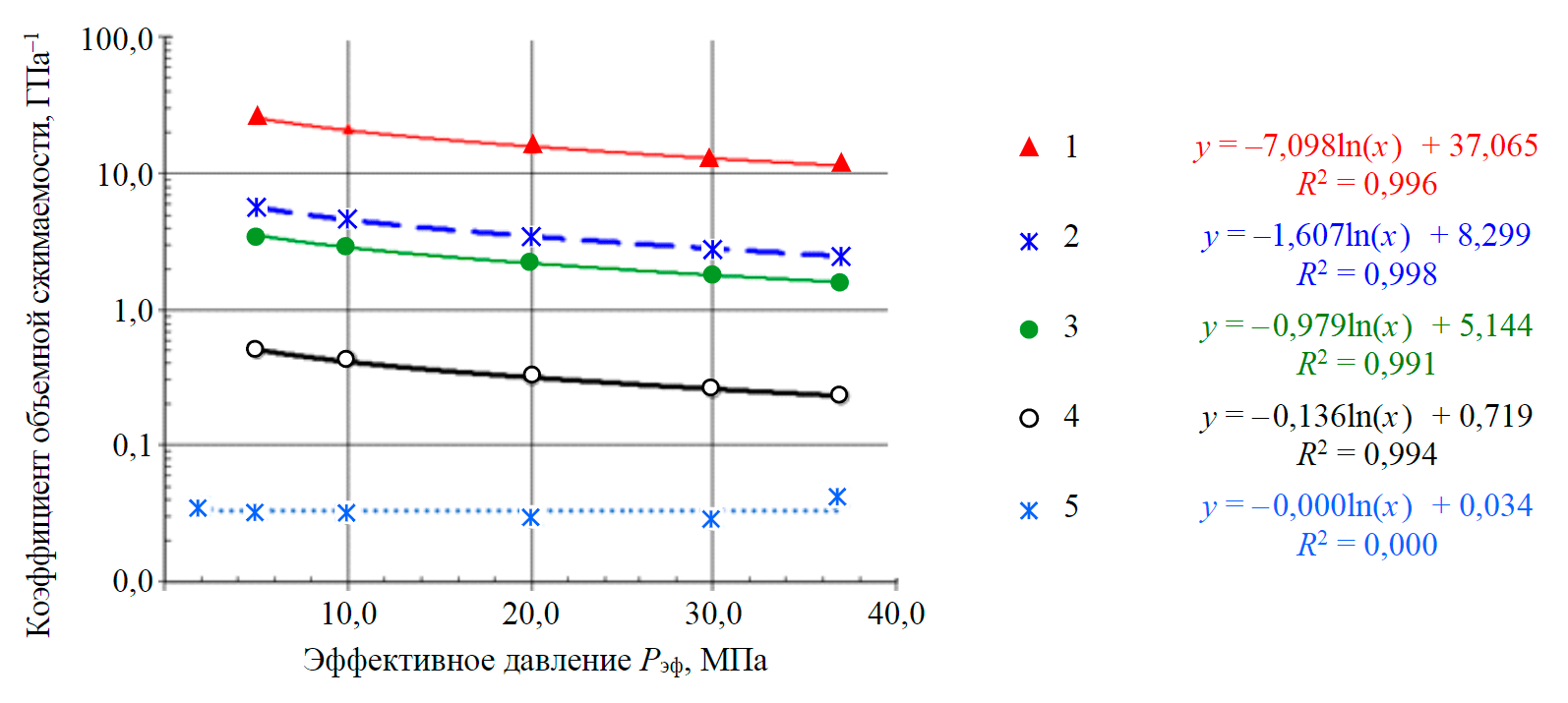
Рис.2. Изменения коэффициентов объемной сжимаемости: минерального скелета, породы, всего порового пространства и его двух компонент (межзерновой и трещинной) от эффективного давления 1 – трещин (формула (19); 2 – общей пористости (формула (15); 3 – межзерновых пор (формула (18); 4 – горной породы (фор-мула (14); 5 – минерального скелета (формула (9)

Обсуждение результатов

Разделение порового пространства на жесткие и мягкие (податливые) поры было рассмотрено и в работах [30, 35], где мягкие поры было предложено идентифицировать как трещины. В работе [37] развивается PDA (pore deformation approach) подход, предложенный С.А.Шапиро [32], где поровое пространство делится на жесткие и податливые части. При этом зависимости пористости и упругих свойств от нагрузки имеют линейный вклад, обусловленный жесткой (межзерновой) частью, и экспоненциальный вклад, обусловленный податливой (трещинной) частью порового пространства, подобно тому, как это показано на рис.1.

В трещиноватых образцах при увеличении эффективного давления происходит резкое снижение и пористости и проницаемости, а в образцах с межзерновой пористостью этого не наблюдается [15].

Значения коэффициентов сжимаемости объема образца, минерального скелета, объема всего порового пространства и отдельно его межзерновой и трещинной компонент для исследуемых горных пород, полученные при увеличении Pэф, позволили оценить их величины при разных давлениях [2, 13, 14], а также выявить их эмпирические зависимости от P_эф, подобные приведенным в работах [31, 33, 36]. Полученные зависимости с высокой степенью достоверности (R² = 0,99) могут быть аппроксимированы логарифмическими уравнениями (рис.2), причем, наибольшие значения коэффициента сжимаемости характерны для трещин, а наименьшие – для межзерновой пористости.

Для более точной оценки просадок земной поверхности в процессе разработки месторождений на истощение имеет значение соотношение величин коэффициентов сжимаемости трещинной и межзерновой компонент пористости к общей сжимаемости объема образца с ростом P_эф. Результаты экспериментальных исследований показали, что отношение коэффициентов сжимаемости трещин и межзерновых пор сохраняется примерно на одном и том же уровне (в среднем 7,85-8,40), который изменяется для разных образцов в диапазоне 26,9-2,46, т.е. изменение объема трещин в среднем почти в восемь раз больше изменения объема межзерновых пор при смене P_эф на одну и ту же величину. Величина коэффициента сжимаемости всего порового пространства входит в диапазон величин коэффициентов сжимаемости трещинной и межзерновой компонент пористости и определяется долей трещинной пористости в общей пористости.

Средняя величина отношения коэффициентов сжимаемости трещин и сжимаемости горной породы с ростом P_эф изменяется в узком диапазоне 54,0-55,3, который варьирует для разных образцов в диапазоне 19,6-105,0. Это свидетельствует о том, что при изменении P_эф на одну и ту же величину относительное изменение объема трещин почти в 55 раз больше относительного изменения объема всего образца.

В 1965 г. J.B.Walsh выявил, что при определенной концентрации узких трещин их влияние на сжимаемость породы аналогично влиянию такого же числа сферических пор диаметром в две трети от длины трещины, но трещинная пористость при этом значительно меньше пористости, обусловленной сферическим порами; чем длиннее трещина в породе, тем больше ее сжимаемость. Быстрое уменьшение сжимаемости трещин на начальном этапе увеличения P_эф можно объяснить закрытием небольшого числа имеющихся длинных трещин.

Определение величин трещинной и межзерновой пористости исследованных горных пород позволило оценить изменения величины коэффициента сжимаемости всего порового пространства в зависимости от долей трещинной m_тр/m и межзерновой m_мз/m пористости при росте P_эф с 2,0 до 37,0 МПа. Выявлено, что с увеличением доли трещинной пористости (рис.3, а) растет и коэффициент сжимаемости порового пространства. В то же время рост доли межзерновой пористости уменьшает коэффициент сжимаемости порового пространства (рис.3, б), поскольку коэффициент сжимаемости трещин существенно больше коэффициента сжимаемости межзерновых пор.

Ранее авторами [5, 6, 39] было выявлено, что с ростом P_эф доля трещинной пористости сокращается, и ее влияние уменьшается. В работах [3, 4, 10, 16] говорится о необходимости учета сжимаемости коллекторов при разработке месторождений и зависимости радиуса зоны фильтрации в разрабатываемых пластах от коэффициентов сжимаемости коллектора. Поэтому определение коэффициента сжимаемости трещин и знание величины трещинной пористости позволит надежнее прогнозировать возможные изменения в коллекторах нефти и газа в процессе изменения напряженного состояния продуктивных пластов с трещинами в процессе разработки месторождений.

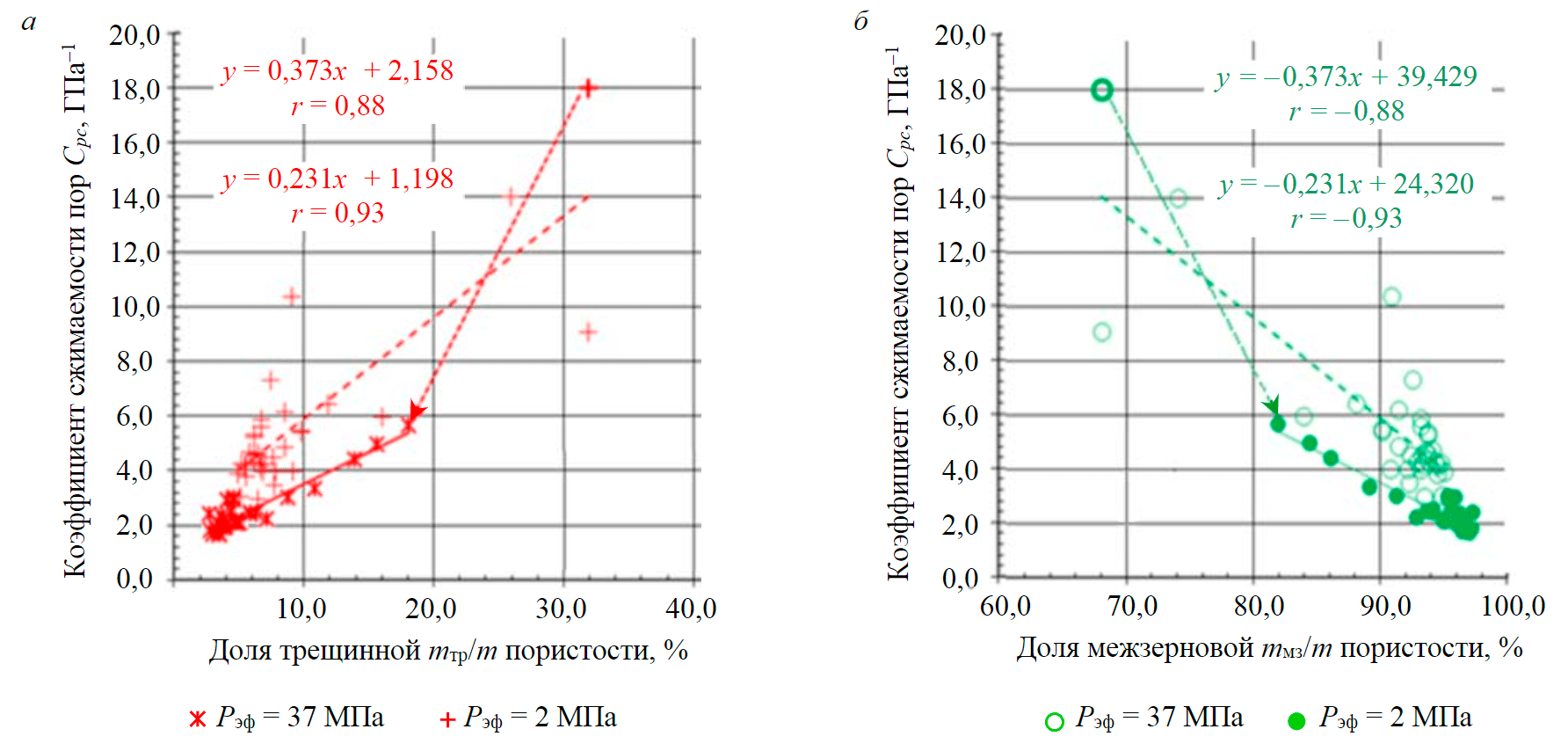
Рис.3. Влияние вклада долей трещинной (а) и межзерновой пористости (б) на коэффициент сжимаемости всего порового пространства при эффективном давлении 2,0 и 37,0 МПа; n = 34. Стрелками показаны изменения параметров при переходе эффективного давления от 2,0 до 37,0 МПа

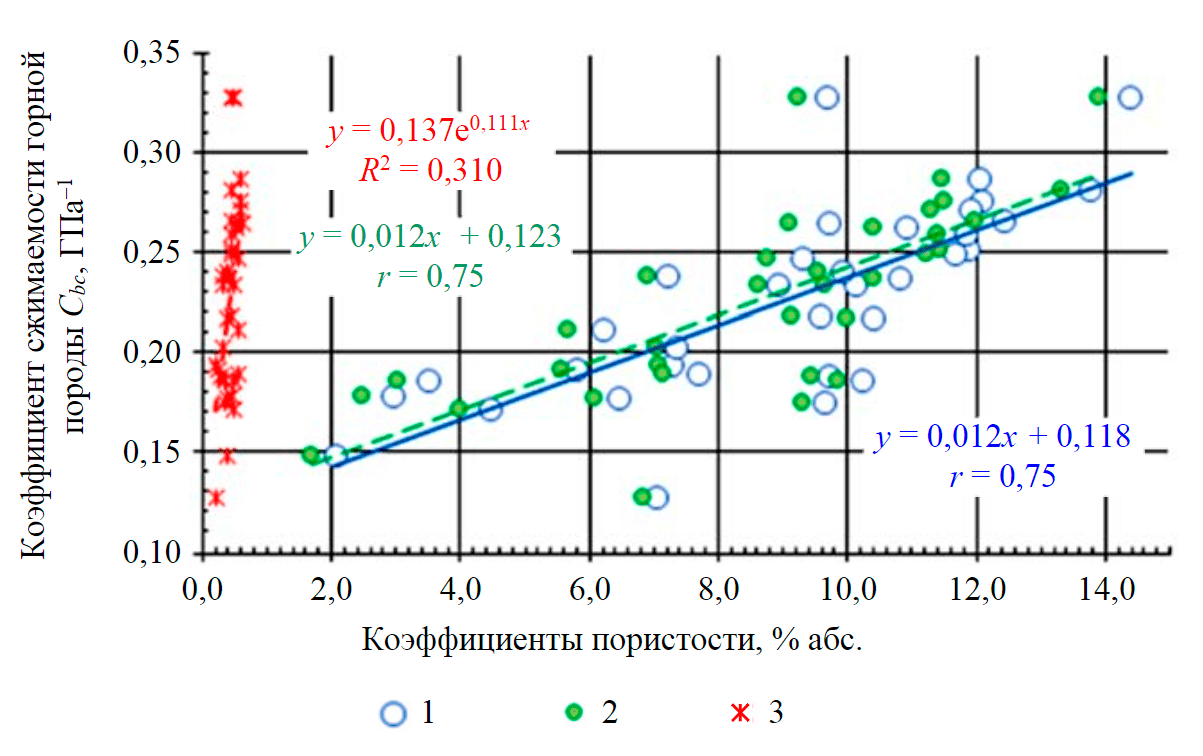
Рис.4. Влияние величины общей (m) пористости и двух ее компонент (межзерновой mмз и трещинной mтр) на коэффициент сжимаемости горной породы при эффективном давлении 37 МПа 1 – от общей пористости, n = 34; 2 – от межзерновой пористости; 3 – от трещинной пористости

Известно, что формирование просадок земной поверхности происходит чаще всего за счет сокращения толщины продуктивных пород в процессе разработки месторождений, и важно определить, какие именно компоненты коэффициента сжимаемости горных пород влияют на него сильнее. Экспериментальные данные показали, что основной вклад в величину коэффициента сжимаемости горных пород вносит величина общей пористости и ее межзерновая компонента (рис.4). Но изменения трещинной пористости оказывают на коэффициент сжимаемости горных пород большее (0,238/0,012 = 19,8) влияние, чем такие же изменения межзерновой пористости.

Экспериментальные результаты показали (см. таблицу), что общая пористость и обе ее компоненты с ростом P_эф уменьшаются, но с разной скоростью: трещинная пористость снижается быстрее. Коэффициенты сжимаемости тоже уменьшаются с различной скоростью по мере роста P_эф.

Заключение

Предложен метод раздельной оценки коэффициентов сжимаемости трещин и межзерновых пор, экспериментально получены их значения и зависимости от эффективного давления. Результаты исследований показали, что наибольшие значения коэффициента сжимаемости характерны для трещин, а наименьшие – для межзерновой пористости. Показано, что коэффициент сжимаемости объема трещин в среднем почти в восемь раз больше коэффициента сжимаемости объема межзерновой пористости и почти в 55 раз больше коэффициента сжимаемости объема исследованных горных пород. Можно ожидать бóльшей сжимаемости всего порового объема горных пород с высокой долей трещинной пористости в связи с тем, что трещины имеют бóльшие значения коэффициента сжимаемости.

Таким образом, определение коэффициентов сжимаемости трещинной и межзерновой пористости позволит повысить достоверность оценок изменений петрофизических параметров коллекторов нефти и газа, обусловленных изменениями напряженного состояния в процессе добычи. Результаты исследований могут быть использованы для учета изменений физических свойств коллекторов и уточнения величины просадок при разработке месторождений нефти газа.

Литература

Влияние эффективного давления на изменение физических и коллекторских свойств горных пород / О.В.Иселидзе, А.В.Дахнов, Е.Б.Григорьев и др. // Вести газовой науки. 2018. № 1(33). С. 95-99. URL: http://vesti-gas.ru/sites/default/files/attachments/vgn-1-33-2018-095-099.pdf
Гасеми М.Ф. Граничные значения параметров строения пустотного пространства петроупругих моделей карбонатных пород / М.Ф.Гасеми, И.О.Баюк // Физика Земли. 2020. № 2. С. 69-88. DOI: 10.31857/S0002333720020039
Городнов А.В. Упругие свойства горных пород при статических и динамических нагрузках / А.В.Городнов, В.Н.Черноглазов, Н.Ш.Равилов // Геофизика. 2017. № 6. С. 19-24. URL: https://elibrary.ru/item.asp?id=32535100
Грачев С.И. К вопросу о двухфазной фильтрации в пористой среде / С.И.Грачев, В.А.Коротенко, О.П.Зотова // Бурение и нефть. 2016. № 5. С. 50-54. URL: https://burneft.ru/archive/issues/2016-05/50
Жуков В.С. Динамика физических свойств коллекторов при разработке месторождений нефти и газа / В.С.Жуков, Е.О.Семенов, Ю.О.Кузьмин // Вести газовой науки. 2018. № 5 (37). С. 82-99. URL: http://vesti-gas.ru/sites/default/files/attachments/vgn-5-37-2018-082-099.pdf
Жуков В.С. Изменения структуры порового пространства коллекторов дагинского горизонта при моделировании пластовых условий / В.С.Жуков, Ю.М.Чуриков, В.В.Моторыгин // Вести газовой науки. 2017. № 3 (31). С. 238-246. URL: http://vesti-gas.ru/sites/default/files/attachments/vgn-3-31-2017-238-246.pdf
Жуков В.С. Оценка трещиноватости коллекторов по скорости распространения упругих волн // Вести газовой науки. 2012. № 1 (9). С. 148-152. URL: http://vesti-gas.ru/sites/default/files/attachments/148-152-geologiya-2012-blok-v26-hq.pdf
Зиновкина Т.С. Об изменении пористости коллекторов в процессе разработки нефтяных месторождений // Нефтяное хозяйство. 2012. № 8. С. 132-137. URL: https://oil-industry.net/Journal/archive_detail.php?ID=9578&art=196454
Кожевников Д.А. Петрофизическое моделирование трещинных коллекторов / Д.А.Кожевников, К.В.Коваленко, А.А.Арсибеков // Каротажник. 2011. № 7 (205). С. 186-192. URL: https://elibrary.ru/item.asp?id=16499970
Коротенко В.А. Интерпретация результатов трассерных исследований с учетом конвективного массопереноса / В.А.Коротенко, С.И.Грачев, А.Б.Кряквин // Записки Горного института. 2019. Т. 236. С. 185-193. DOI: 10.31897/PMI.2019.2.185
Кузьмин Ю.О. Научно-методические основы обеспечения геодинамической безопасности объектов нефтегазового комплекса // Записки Горного института. 2010. Т. 188. С. 158-162. URL: https://pmi.spmi.ru/index.php/pmi/article/view/6601
Кузьмин Ю.О. Еще раз об оценке оседания дна акватории в случае разработки сеноманской залежи одного газового месторождения // Маркшейдерский вестник. 2010. № 1 (75). С. 53-60.
Мартюшев Д.А. Влияние напряженного состояния горных пород на матричную и трещинную проницаемость в условиях различных литолого-фациальных зон турне-фаменских нефтяных залежей Верхнего Прикамья / Д.А.Мартюшев, С.В.Галкин, В.В.Шелепов // Вестник Московского университета. Серия 4: Геология. 2019. № 5. С. 44-52. DOI: 10.33623/0579-9406-2019-5-44-52
Мартюшев Д.А. Определение раскрытости и сжимаемости естественных трещин карбонатной залежи Логовского месторождения / Д.А.Мартюшев, А.В.Лекомцев, А.Г.Котоусов // Вестник Пермского национального исследовательского политехнического университета. Геология. Нефтегазовое и горное дело. 2015. № 16. С. 61-69. DOI: 10.15593/2224-9923/2015.16.7
Мартюшев Д.А. Оценка влияния напряженного состояния горных пород на проницаемость карбонатных коллекторов // Известия Томского политехнического университета. Инжиниринг георесурсов. 2020. Т. 331. № 9. С. 7-17. DOI: 10.18799/24131830/2020/8/2765
Оценка влияния градиентов водонасыщенности и капиллярного давления на формирование размера зоны двухфазной фильтрации в сжимаемом низкопроницаемом коллекторе / В.А.Коротенко, С.И.Грачев, Н.П.Кушакова, С.Ф.Мулявин // Записки Горного института. 2020. Т. 245. С. 569-581. DOI: 10.31897/PMI.2020.5.9
Паникаровский В.В. Определение устойчивости пород при эксплуатации сеноманских залежей / В.В.Паникаровский, Е.В.Паникаровский, В.Н.Дубровский // Известия высших учебных заведений. Нефть и газ. 2010. № 3. С. 43-47. URL: https://elibrary.ru/item.asp?id=15177548
Патент № 2516392 РФ. Способ определения трещинной пористости пород / В.С.Жуков. Опубл. 20.05.2014. Бюл. №8.
Повышение эффективности разработки месторождений углеводородов на основе комплексных геомеханических исследований / Ю.А.Кашников, С.Г.Ашихмин, Д.В.Шустов и др. // Нефтяное хозяйство. 2019. № 3. С. 66-69. DOI: 10.24887/0028-2448-2019-3-66-69
Руденко В.В. Комплексирование геолого-технологической модели месторождения нефти и методов мониторинга за сдвижением земной поверхности для обеспечения безопасности подрабатываемых объектов / В.В.Руденко, И.М.Галиулин // Горный информационно-аналитический бюллетень. 2014. № 4. С. 180-184. URL: https://www.elibrary.ru/item.asp?id=21391994
Рыжов А.Е. Структура порового пространства пород-коллекторов ботуобинского горизонта Чаяндинского месторождения / А.Е.Рыжов, Т.А.Перунова, Д.М.Орлов // Вести газовой науки. 2011. № 1 (6). С. 162-174. URL: http://vesti-gas.ru/sites/default/files/attachments/162-174-sbornik_plasty_ch1_v4.pdf
Туранк К. Распространение волн и границы раздела в породах / К.Туранк, Д.Фурментро, А.Денни // Механика горных пород применительно к проблемам разведки и добычи нефти. М.: Мир, 1994. С. 176-184.
Учет геомеханических свойств пласта при разработке многопластовых нефтяных месторождений / С.В.Галкин, С.Н.Кривощеков, Н.Д.Козырев и др. // Записки Горного института. 2020. Т. 244. С. 408-417. DOI 10.31897/PMI.2020.4.3
Chertov M.A. Practical Laboratory Methods for Pore Volume Compressibility Characterization in Different Rock Types / M.A.Chertov, R.Suarez-Rivera // 48th US Rock Mechanics / Geomechanics Symposium held (ARMA’14-7532), 1-4 June 2014, Minneapolis: CRC Press, 2014. 14 p. URL: https://www.researchgate.net/publication/267675512_Practical_Laboratory_Methods_for_Pore_Volume_Compressibility_Characterization_in_Different_Rock_Types
Chin L. Modeling of Subsidence and Reservoir Compaction under Waterflood Operations / L.Chin, N.Nagel // International Journal of Geomechanics. 2004. Vol. 4. Iss. 1. P. 28-34. DOI: 10.1061/(ASCE)1532-3641(2004)4:1(28)
Guilbot J. 4-D constrained depth conversion for reservoir compaction estimation: Application to Ekofisk Field / J.Guilbot, B.Smith // The Leading Edge. 2002. Vol. 21. Iss. 3. P. 302-308. DOI: 10.1190/1.1463782
Lewis R.W. Fully coupled modeling of seabed subsidence and reservoir compaction of North Sea oil fields / R.W.Lewis, W.K.S.Pao, A.Makurat // Hydrogeology Journal. 2003. Vol. 11. P. 142-161. DOI: 10.1007/s10040-002-0239-z
Mavko G. The Rock Physics Handbook, Second Edition / G.Mavko, T.Mukerji, J.Dvorkin. New York: Cambridge University Press, 2009. 525 р.
Nagel N. Compaction and subsidence issues within the petroleum industry: From Wilmington to Ekofisk and beyond // Physics and Chemistry of The Earth, Part A: Solid Earth and Geodesy. 2001. Vol. 26. Iss. 1-2. P. 3-14. DOI:10.1016/S1464-1895(01)00015-1
Permeability dependency on and compliant porosities: a model and some experimental examples / S.A.Shapiro, G.P.Khizhniak, V.V.Plotnikov et al. // Journal of Geophysics and Engineering. 2015. Vol. 12. Iss. 3. P. 376-385. DOI: 10.1088/1742-2132/12/3/376
Schutjens P. On the pore volume compressibility and its application as a petrophysical parameter / P.Schutjens, W.Heidug // 9th Biennial International Conference and Exposition on Petroleum Geophysics, 16-18 February 2012, Hyderabad, India. SPG, 2012. № P-512. URL: https://www.spgindia.org/spg_2012/spgp512.pdf
Shapiro S.A. Elastic piezosensitivity of porous and fractured rocks // Geophysics. 2003. Vol. 68. Iss. 2. P. 482-486. DOI: 10.1190/1.1567215
Sheng Guanlong. Effect of microscale compressibility on apparent porosity and permeability in shale gas reservoirs / Sheng Guanlong, Javadpour Farzam, Su Yuliang // International Journal Heat and Mass Transfer. 2018. Vol. 120. P. 56-65. DOI: 10.1016/j.ijheatmasstransfer.2017.12.014
Shenglai Yang. Fundamentals of Petrophysics. Second Edition. Beijing: Springer Geophysics and Petroleum Industry Press, 2017. 502 p. DOI: 10.1007/978-3-662-55029-8
Stiff- and compliant-porosity based model of permeability – Theory and experiments: Conference Proceedings / S.A.Shapiro, G.P.Khizhniak, V.V.Plotnikov et al. // 77th EAGE Conference and Exhibition, 1-4 June 2015, Madrid, Spain. European Association of Geoscientists & Engineers, 2015. P. 2812-2816. DOI: 10.3997/2214-4609.201412949
Stress-dependence of the permeability and porosity of sandstone and shale from TCDP Hole-A / Jia-Jyun Dong, Jui-Yu Hsu, Wen-Jie Wu et al. // International Journal of Rock Mechanics and Mining Sciences. 2010. Vol. 47. Iss. 7. P. 1141-1157. DOI: 10.1016/j.ijrmms.2010.06.019
Sviridov V.A. Elastic properties of two VTI shale samples as a function of uniaxial stress: Experimental results and application of the porosity-deformation approach / V.A.Sviridov, S.I.Mayr, S.A.Shapiro // Geophysics. 2017. Vol. 82. Iss. 6. P. 201-210.
Tiab D. Petrophysics: theory and practice of measuring reservoir rock and fluid transport properties / D.Tiab, E.C.Donaldson. Oxford: Gulf Professional Publishing – Elsevier, 2015. 918 p.
Zhukov V.S. The Influence of Fracturing of the Rocks and Model Materials on P-wave Propagation Velocity: Experimental Studies / V.S.Zhukov, Yu.O.Kuzmin // Izvestiya, Physics of the Solid Earth. 2020. Vol. 56. P. 470-480. DOI: 10.31857/S0002333720040109
Zimmerman R.W. Compressibility and shear compliance of spheroidal pores: Exact derivation via the Eshelby tensor, and asymptotic expressions in limiting cases / R.W.Zimmerman, E.C.David // International Journal of Solids and Structures. 2011. Vol. 48. Iss. 5. P. 680-686. DOI: 10.1016/j.ijsolstr.2010.11.001
Zimmerman R.W. Introduction to Rock Properties // The Imperial College Lectures in Petroleum Engineering. 2017. Vol. 3. P. 1-46.
Zimmerman R.W. Pore Volume and Porosity Changes under Uniaxial Strain Conditions // Transport in Porous Media. 2017.Vol. 119. P. 481-498. DOI: 10.1007/s11242-017-0894-0
Zoback M.D. Reservoir geomechanics. New York: Cambridge University Press. 2007. 505p. DOI: 10.1017/CBO9780511586477