Experimental evaluation of compressibility coefficients for fractures and intergranular pores of an oil and gas reservoir
- 1 — Ph.D., Dr.Sci. Chief Researcher Schmidt Institute of Physics of the Earth of the Russian Academy of Sciences ▪ Orcid ▪ Elibrary
- 2 — Ph.D., Dr.Sci. Deputy Director Schmidt Institute of Physics of the Earth of the Russian Academy of Sciences ▪ Orcid
Abstract
The paper is devoted to studies of the volumetric response of rocks caused by changes in their stress state. Changes in the volume of fracture and intergranular components of the pore space based on measurements of the volume of pore fluid extruded from a rock sample with an increase in its all-round compression have been experimentally obtained and analyzed. Determination of the fracture and intergranular porosity components is based on the authors' earlier proposed method of their calculation using the values of longitudinal wave velocity and total porosity. The results of experimental and analytical studies of changes in porosity and its two components (intergranular and fractured) under the action of effective stresses are considered. This approach allowed the authors to estimate the magnitude of the range of changes in the volumetric compressibility of both intergranular pores and fractures in a representative collection of 37 samples of the Vendian-age sand reservoir of the Chayanda field. The method of separate estimation of the compressibility coefficients of fractures and intergranular pores is proposed, their values and dependence on the effective pressure are experimentally obtained. It is determined that the knowledge of the values of fracture and intergranular porosity volumetric compressibility will increase the reliability of estimates of changes in petrophysical parameters of oil and gas reservoirs caused by changes in the stress state during the development of hydrocarbon fields.
Introduction
Development of oil, gas and solid minerals requires consideration of the elastic volumetric response of rocks caused by changes in their stress state [28, 34, 43]. Due to the complex structure of rock pore space, consisting of intergranular pores and fractures [2, 4], changes in the volume of each of the components requires independent consideration and analysis [5, 6]. A relevant task is the analysis and estimation of the magnitude for deformation of intergranular pores and fractures, which arise due to changes in the stress state of the reservoir caused by hydrocarbon production [5, 11, 23]. Thus, work [19] noted the need to take into account the dependence of permeability and porosity properties of pore- and fracture-type reservoirs on changes in the stress state during the development of oil and gas fields. “Compressibility of fractures can differ from compressibility of the matrix by an order of magnitude. For example, in naturally fractured reservoirs in the Kirkuk (Iraq) and Asmari (Iran) fields, fracture compressibility varies between 6-60 GPa–1. At the Groznenskoe field, fracture compressibility varies from 10 to 100 GPa–1. At all these fields the fracture compressibility is 10-100 times higher than the compressibility of the intergranular matrix, and to assume that they are equal is unacceptable practice” [38].
Theory of the problem
Коefфициент объемной сжимаемости – это парамеf, количественно определяющий зависимость между давлением, оказываемым на тело, и результирующим изменением его объема. Материал без пор и fещин имеет единственную сжимаемость, определяемую формулой:
where V0 – body volume at initial pressure; P – hydrostatic pressure exerted on its outer surface.
There are two independent volumes (sample and pores) and two pressures (universal compression and pore fluid) which can be varied; four different compressibilities can be associated with a porous rock [40, 41]. In each of these compressible porous rocks, changes in either pore volume Vp or rock sample volume Vb are associated with changes in pore pressure Pp or universal pressure Pc. They are described using notations in which the first index indicates the corresponding change in volume and the second index indicates the changing pressure. These compressibility coefficients are most clearly defined in [42]:
- compressibility of the rock volume with changes in universal pressure
- compressibility of the rock volume with changes in pore pressure
-
compressibility of the pore volume with changes in pore pressure
- сжимаемость объема пор при изменении порового давления
The concept of effective pressure also needs to be covered
where Рс – pressure of the universal compression; Рр – pressure of the pore (formation) fluid (water, oil, gas); a – Biot coefficient (sometimes called the unloading coefficient) describes that part of the pore pressure which counteracts the universal pressure.
For rocks with a porosity greater than 5 %, a is often assumed to be 1. In this case, Cpc and Cpp are equal to each other. In other words, the same changes in the total and pore pressures change the pore volume by the same amount, but with the opposite sign: an increase in the universal compression and a decrease in the pore pressure lead to a decrease in the pore volume.
In order to account for the elastic energy of the entire sample (formation, deposit), the elasticity of both the rock skeleton (solid matrix) and all formation fluids must be taken into account. In this case, the term “total compressibility” [34], or compressibility of the rock (sample) volume, should be used to represent the elasticity of the entire deposit:
In general, with three phases (oil, water and gas) present simultaneously in the formation, the mathematical expression for the relationship between them and the total compressibility of the rock volume is as follows [34]:
where Coil, Cgas, Cwater и Csk – compressibility of oil, gas, water and solid matrix (skeleton) of the rock, respectively; m – porosity of the rock; Soil, Sgas, Swater – oil, gas, water content (saturation) in the pore space of the rock, respectively.
During the petrophysical investigations, the pressure and temperature of the pore fluid (formation water model) were maintained at the same level of 13 MPa and 20 °С, only universal pressure was increased (from 15 to 50 MPa). Therefore, the compressibility coefficient of the Cwater fluid does not need to be taken into account.
Value of the compressibility coefficient for a solid rock matrix can be determined experimentally by means of so-called unjacketed tests [34, 42]. In these tests the rock is pressurised by a fluid (liquid), which penetrates into the pores of the rock, so that the universal pressure and the pore fluid pressure are the same. But unfortunately, the installation used did not permit this kind of test and the compressibility coefficient of the rock mineral matrix was calculated dynamically, based on elastic wave propagation velocity and rock density:
where Csk – compressibility coefficient of the mineral matrix (skeleton), GPa–1; vp – longitudinal wave velocity, km/s; vs – shear wave velocity, km/s; δ – density, g/cm3; μ – Poisson's ratio (dynamic).
The Cpc and Cpp compressibilities are pore compressibilities and express the effect of pressure changes on the volume of cavern space contained within the rock. The Cpp pore compressibility is used in reservoir analysis because it reflects the volume of excess pore fluid that may be stored in the pore space due to increased pore pressure. This compressibility is added to the compressibility of the formation fluid Cf to represent their sum as the formation compressibility, which is used in the basic formation equation. In this case, pore pressure and universal pressure are assumed to be independent variables; physically, this corresponds to what is known as drained compression (open pore system), in which changes in universal pressure do not cause changes in pore pressure. A closed pore system results in undrained compression with an increase in universal compression, but is not usually a reservoir, as fluid cannot be extracted from these pores without additional action to create additional filtration channels.
Changes in the volumetric deformation of the sample and the volumetric deformation of the pores can be expressed in terms of compressibility of the porous rock:
Since fluid saturated sandstone can be considered as a homogeneous material, Cbc is its effective volumetric compressibility as an analogue of the compressibility of a non-porous material. Another volumetric compressibility Cbp, which has been called pseudo-volumetric [25], reflects the effect of pore pressure on the total volume of a rock sample [17]. This compressibility is useful in calculations of land or seabed subsidence in hydrocarbon fields development [12, 20, 25].
When the pore fluid (oil, water, gas) is extracted from the formation (underground deposits), the pressure of the fluid in the pores decreases and the total volume occupied by the deposit (formation) decreases according to equation (7). Subsequent subsidence of the ground surface above the deposit can amount to tens of meters. Subsidence causes significant damage to buildings and other structures. Well-known examples of oilfield subsidence are Wilmington Long Beach in Southern California [29] and Ecofisk in the North Sea [26, 27].
Methodology of the investigation
Experimental investigations were carried out under universal compression growth conditions only, in contrast to ARMA-14-7532 [24], which provides for additional uniaxial compression. The technique used allowed measuring the volume of pore fluid displaced from the sample when increasing the compression and calculating both changes in porosity and estimating the volumetric deformation. This was calculated taking into account that the compressibility coefficient of the solid rock matrix is several orders of magnitude greater than the compressibility coefficient of the pore space.
The porosity under formation simulation conditions was determined (taking into account the volume of fluid displaced from the pore space of the rock sample) using the formula:
where matm – porosity coefficient under atmospheric conditions, %; ΔVp – volume of pore fluid displaced from the sample (pore volume change), cm3; V – initial sample volume, cm3.
The volumetric deformation of the sample, taking into account that the compressibility of the mineral skeleton is two orders of magnitude lower than that of the liquid, was calculated using the formula:
The rock volume compressibility coefficient was determined according to the formula:
where ΔPef – changes in effective pressure, GPa.
For the convenience of working with negative numbers of compressibility coefficients, we will consider volume reduction to be positive, which is equivalent to multiplying by –1 the expressions (1), (2) and (4), in which volume increase is assumed to be positive.
The compressibility coefficient of the pore space was determined using the formula:
Since m = Vp/V, as noted in [34], Ct = Cpcm. Thus, from formulas (4) and (5) the rock volume compressibility (14) and pore volume compressibility (total porosity) (15) have been determined by changing the effective pressure.
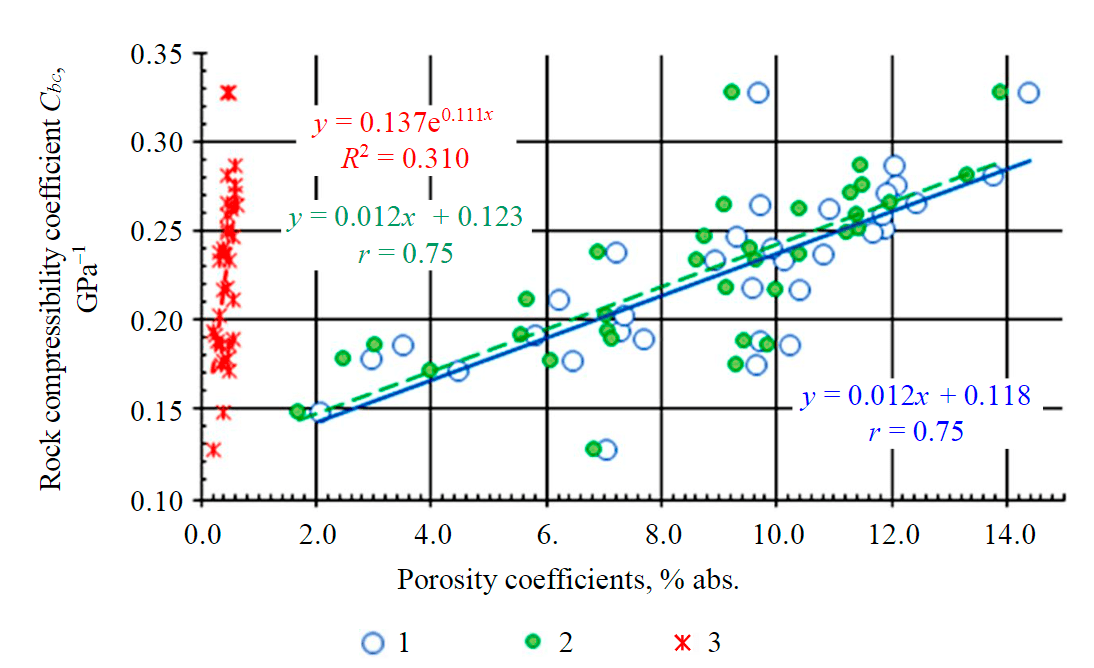
Fig.1. Changes in porosity coefficient (а) and volumetric deformation of the sample (b) on effective pressure
Results
34 sandy-clay samples of Vendian age were investigated, having under atmospheric conditions porosity coefficient of 3-15.6 %, permeability coefficient of 2-100 mD, made from the rock sample raised from 1660-1860 m depth. The samples are represented mainly by coarse- to fine-grained quartz and quartz-feldspar sandstones with mixed quartz-regeneration, sulphate, clay-film and partly basal cement.
Values of porosity coefficient for rock samples (Fig.1, a) from Chayandinskoe oil-gas-condensate field (COGCM) and volume deformation of rock samples (Fig.1, b) obtained at current Pef values allowed obtaining their dependence on the growth of effective pressure in the formation in the same way as shown in [1, 8, 23]. Changes of volumetric deformation for samples correspond to changes in porosity caused by growth of Pef.
It is well known that the pore space of rock samples consists of two components: intergranular and fracture space. Fracture porosity is expressed as the ratio of fracture volume to total rock volume:
Intergranular porosity is expressed as the ratio of the volume of intergranular space to the total volume of the rock:
Previously, a method for determining the magnitude of these components has been proposed, based on measuring the value of elastic longitudinal wave propagation velocity [7, 18, 22]. The total porosity and the longitudinal wave velocity were determined at each step of Pef. With increasing universal pressure the pore fluid pressure remained unchanged and hence the Pef increased. The compressibilities of intergranular and fracture porosity and rock volume compressibility coefficients (14), intergranular (16) and fracture (17) porosities, were determined using the expressions:
where ΔVig and ΔVf – changes in the volume of intergranular space and fracture hollowness, respectively.
This technique allowed experimental estimation of fracture and intergranular porosity with Pef increase and separate calculation of compressibility coefficients for sample volume, mineral matrix, fracture, intergranular porosity of rock samples during Pef increase in simulation of hydrocarbon field development process (Table).
Average values of porosity and volumetric compressibility at different values of effective pressure
|
Coefficients |
Effective pressure Рef, MPa |
|||||
|
2.0 |
5.0 |
10.0 |
20.0 |
30.0 |
37.0 |
|
|
Porosity: |
|
|
|
|
|
|
|
total m, % |
9.926 |
9.681 |
9.505 |
9.302 |
9.163 |
9.088 |
|
intergranular mig, % |
9.178 |
9.025 |
8.912 |
8.783 |
8.694 |
8.657 |
|
fracture mf, % |
0.749 |
0.656 |
0.593 |
0.519 |
0.468 |
0.432 |
|
Compressibility: |
|
|
|
|
|
|
|
Mineral skeleton (dynamic, Csk), GPa–1 |
0.036 |
0.033 |
0.032 |
0.030 |
0.030 |
0.029 |
|
rock Сbc, GPa–1 |
|
0.491 |
0.422 |
0.312 |
0.255 |
0.227 |
|
pore space Cpc, GPa–1 |
|
5.656 |
4.705 |
3.451 |
2.814 |
2.501 |
|
intergranular pores Cig, GPa–1 |
|
3.484 |
3.009 |
2.241 |
1.798 |
1.563 |
|
fracture Сf, GPa–1 |
|
25.35 |
21.30 |
15.62 |
12.64 |
11.62 |
Discussion
Division of the pore space into hard and soft (pliable) pores has also been considered in [30, 35], where soft pores have been proposed to be identified as fractures. In [37], the PDA (pore deformation approach) proposed by Shapiro [32] is developed where the pore space is divided into hard and pliable parts. Dependencies of porosity and elastic properties on load have a linear contribution due to the hard (intergranular) part and an exponential contribution due to the pliable (fractured) part of the pore space, similar to the one shown in Fig.1.
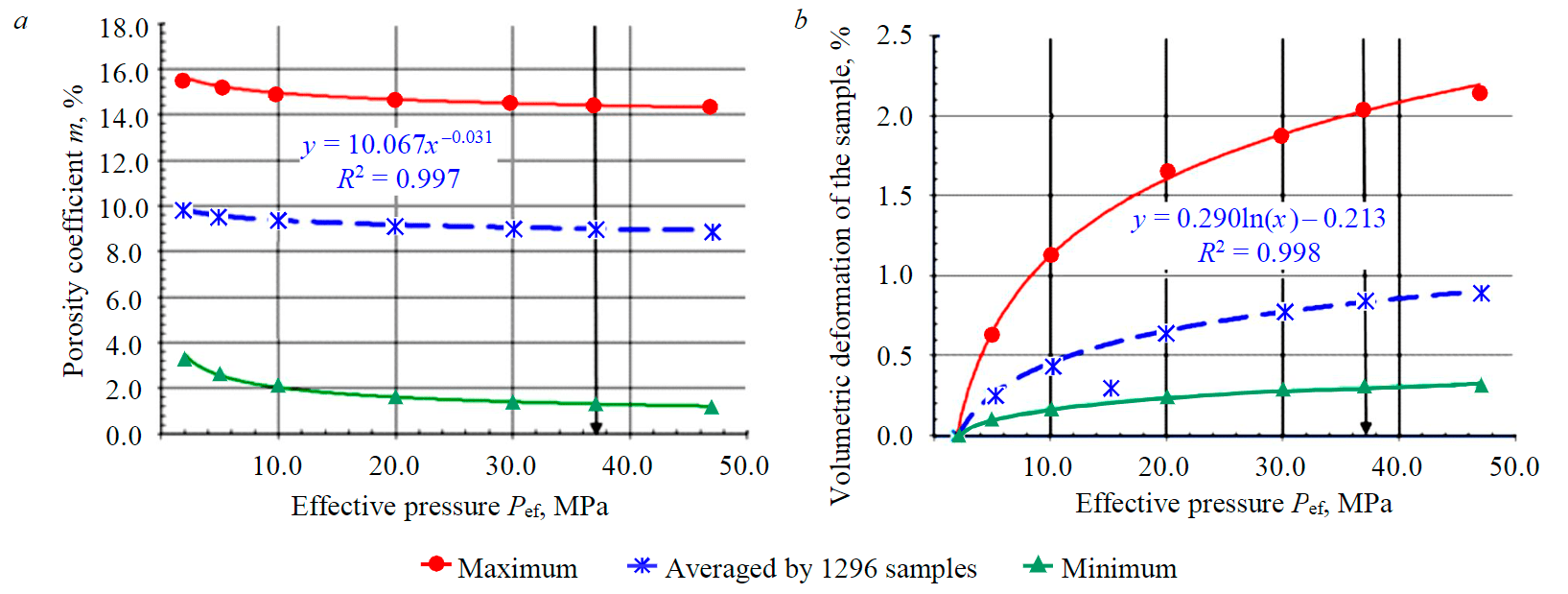
Fig.2. Variation of volumetric compressibility coefficients: mineral skeleton, rock, total pore space and its two components (intergranular and fracture) on the effective pressure 1 – fractures (equation (19); 2 – total porosity (equation (15); 3 – intergranular pores (equation (18); 4 – rock (formula (14); 5 – mineral skeleton (equation (9)
In fractured samples, both porosity and permeability are drastically reduced when the effective pressure is increased, whereas this is not the case in samples with intergranular porosity [15].
Values of compressibility coefficients for the sample volume, mineral skeleton, volume of the total pore space and separately its intergranular and fracture components for the studied rocks, obtained by increasing Pef, allowed estimating their values at different pressures [2, 13, 14], and also revealing their empirical dependences on Pef, similar to those given in papers [31, 33, 36]. The obtained dependencies with high reliability (R2 = 0.99) can be approximated by the logarithmic equations (Fig.2), at that, the highest values of compressibility coefficient are characteristic for fractures, and the lowest ones – for intergranular porosity
For a more accurate assessment of surface subsidence in the process of field development on the depletion, the ratio of the values for the compressibility coefficients of the fracture and intergranular components of porosity to the total compressibility of the sample volume with the growth of Pef is important. Results of experimental investigations have shown that the ratio of compressibility coefficients of fracture and intergranular pores keeps approximately at the same level (on the average 7.85-8.40), which varies for different samples in the range 26.9-2.46, that is the change of fracture volume on the average almost eight times more than the change of intergranular pores volume at that same value of Pef. Value of the compressibility coefficient of the total pore space enters into the range of values for the compressibility coefficients of fracture and intergranular porosity components and is determined by the share of fracture porosity in total porosity.
Average value for the ratio of fracture compressibility coefficients to rock compressibility with increase of Pef changes in a narrow range 54.0-55.3, which varies for different samples in the range 19.6-105.0. This indicates that when Pef changes by the same value, the relative change in fracture volume is almost 55 times greater than the relative change in the volume of the total sample.
In 1965 J.B.Walsh has revealed that at a certain concentration of narrow fractures their influence on rock compressibility is similar to the influence of the same number of spherical pores with diameter of two thirds of fracture length, but the fracture porosity at that is much less than porosity caused by spherical pores; the longer a fracture in the rock, the greater its compressibility. The rapid decrease in fracture compressibility at the initial stage of increasing Pef can be explained by the closure of a small number of existing long fractures.
Determination of fracture and intergranular porosity values of the studied rocks allowed estimating changes in the value of the compressibility coefficient for the entire pore space depending on the share of fracture mf/m and intergranular mig/m porosity when Pef grows from 2.0 to 37.0 MPa. It was found that the compressibility coefficient of the pore space also increases with increasing share of fracture porosity (Fig.3, a). At the same time, the increase of intergranular porosity share decreases the compressibility coefficient of pore space (Fig.3, b), because the compressibility coefficient of fractures is significantly higher than the compressibility coefficient of intergranular pores.
Previously, the authors [5, 6, 39] revealed that with the growth of Pef, the share of fracture porosity decreases and its influence reduces. Works [3, 4, 10, 16] note the necessity to take into account compressibility of reservoirs during development of fields and dependence of filtration zone radius
in the developed formations on the compressibility coefficient of the reservoir. Therefore, determining the compressibility coefficient of fractures and knowledge on the value of fracture porosity will allow reliable prediction of the possible changes in oil and gas reservoirs in the process of changing the stress state of productive formations with fractures in the development of the fields.
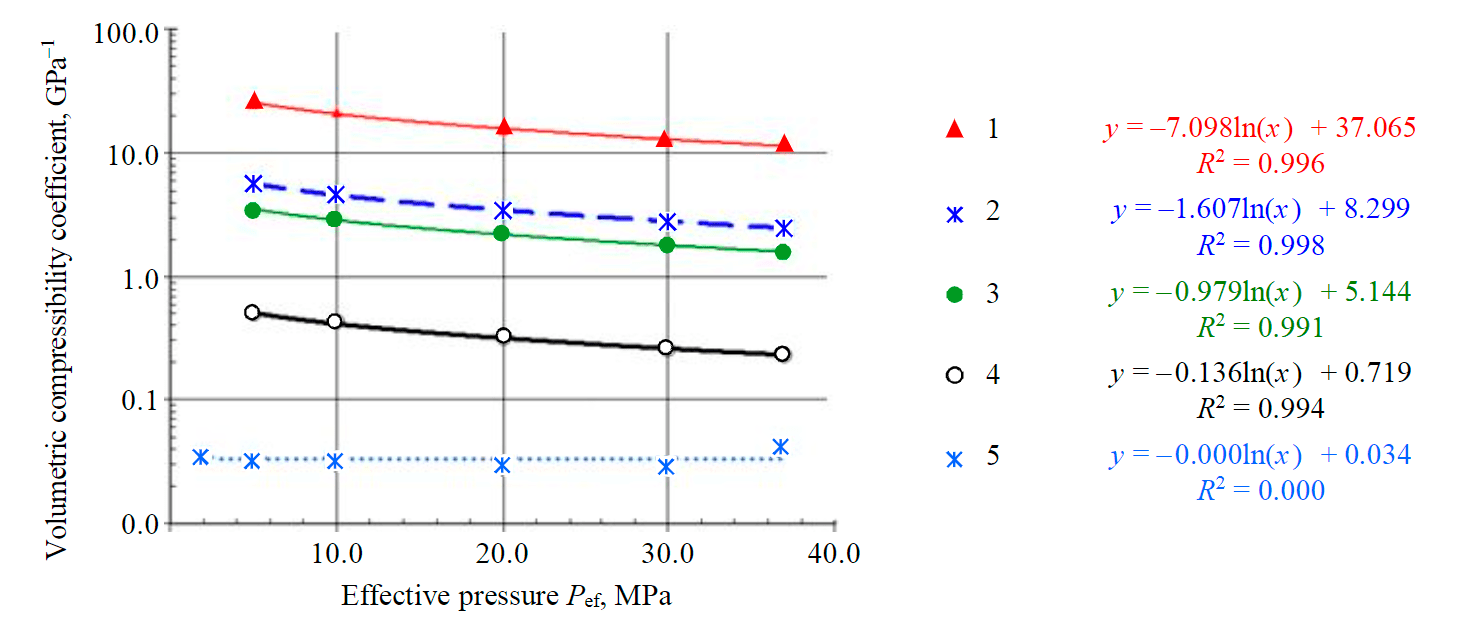
Fig.3. Effect of fracture (a) and intergranular porosity (b) on the compressibility coefficient of the entire pore space at effective pressures of 2.0 and 37.0 MPa; n = 34. The arrows show the changes in of parameters at transition of effective pressure from 2.0 to 37.0 MPa
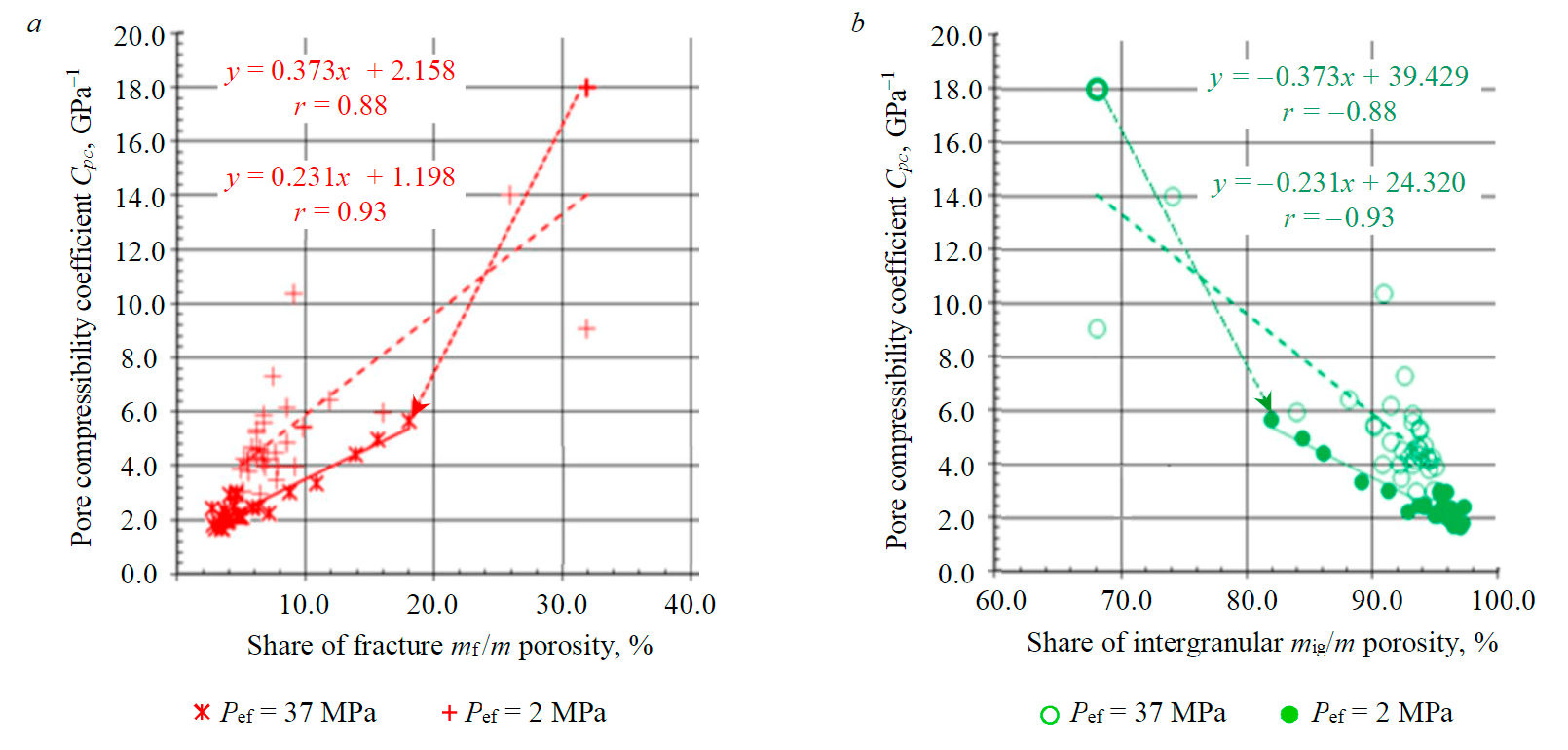
Fig.4. Influence of total (m) porosity and its two components (intergranular mig and fracture mf) on compressibility coefficient of rock at an effective pressure of 37 MPa 1 – total porosity, n = 34; 2 – intergranular porosity; 3 – fracture porosity
It is known that the formation of land surface subsidence occurs most often due to the reduction in thickness of productive rocks during field development, and it is important to determine which components of the rock compressibility coefficient have a stronger influence on it. Experimental data showed that the main contribution to the value of rock compressibility coefficient is made by the value of total porosity and its intergranular component (Fig.4). But changes in fracture porosity have greater (0.238/0.012 = 19.8) influence on rock compressibility coefficient than the same changes in intergranular porosity.
Experimental results have shown (see table) that total porosity and both its components decrease as Pef grows, but at different rates: fracture porosity decreases faster. The compressibility coefficients also decrease at different rates as Pef increases.
Conclusion
The method of separate estimation of compressibility coefficients for fractures and intergranular pores has been proposed, their values and dependence on effective pressure have been experimentally obtained. The results have shown that the highest values of the compressibility coefficient are characteristic for fractures, and the lowest – for intergranular porosity. It is shown that the compressibility coefficient of fracture volume on average is almost eight times greater than the compressibility coefficient of intergranular porosity volume and almost 55 times greater than the compressibility coefficient of the investigated rocks volume. A higher compressibility of the entire pore volume of rocks with a high share of fractured porosity can be expected due to the fact that fractures have a higher compressibility coefficient.
Thus, the determination of fracture and intergranular porosity compressibility coefficients will improve the reliability of estimates for changes in petrophysical parameters of oil and gas reservoirs caused by changes in stress state during production. The results of the research can be used to account for changes in physical properties of reservoirs and to refine the value of subsidence during oil and gas field development.
References
- Iselidze O.V., Dakhnov A.V., Grigorev E.B. et al. Effect of effective pressure on changes in physical and reservoir properties of rocks. Vesti gazovoi nauki. 2018. N 1 (33), p. 95-99 (in Russian).
- Gasemi M.F., Bayuk I.O. Boundary values of the cavern space structure of petroelastic models of carbonate rocks. Fizika Zemli. 2020. N 2, p. 69-88. DOI: 10.31857/S0002333720020039 (in Russian).
- Gorodnov A.V., Chernoglazov V.N., Ravilov N.Sh. Elastic properties of rocks under static and dynamic loads. Geofizika. 2017. N 6, p. 19-24 (in Russian).
- Grachev S.I., Korotenko V.A., Zotova O.P. On the question of two-phase filtration in porous medium. Burenie i neft. 2016. N 5, p. 50-54 (in Russian).
- Zhukov V.S., Semenov E.O., Kuzmin Yu.O. Dynamics of physical reservoir properties in oil and gas field development. Vesti gazovoi nauki. 2018. N 5 (37), p. 82-99 (in Russian).
- Zhukov V.S., Churikov Yu.M., Motorygin V.V. Changes in the structure of the pore space of the Daginsky reservoirs when simulating formation conditions. Vesti gazovoi nauki. 2017. N 3 (31), p. 238-246 (in Russian).
- Zhukov V.S. Assessment of reservoir fracturing by elastic wave propagation velocity. Vesti gazovoi nauki. 2012. N 1 (9), p. 148-152 (in Russian).
- Zinovkina T.S. On changes in reservoir porosity during oil field development. Neftyanoe khozyaistvo. 2012. N 8, p. 132-137 (in Russian).
- Kozhevnikov D.A., Kovalenko K.V., Arsibekov A.A. Petrophysical modelling of fracture reservoirs. Karotazhnik. 2011. N 7 (205), p. 186-192 (in Russian).
- Korotenko V.A., Grachev S.I., Kryakvin A.B. Interpretation of the tracer investigation results considering convective mass transfer. Journal of Mining Institute. 2019. Vol. 236, p. 185-193. DOI: 10.31897/PMI.2019.2.185 (in Russian).
- Kuzmin Yu.O. Scientific and methodological basis for geodynamic safety of oil and gas facilities. Journal of Mining Institute. 2010. Vol. 188, p. 158-162 (in Russian).
- Kuzmin Yu.O. Again on the assessment of seabed subsidence in the case of development of a Cenomanian deposit of one gas field. Marksheiderskii vestnik. 2010. N 1 (75), p. 53-60 (in Russian).
- Martyushev D.A., Galkin S.V., Shelepov V.V. Influence of rock stress state on matrix and fracture permeability under different lithological and facial zones of the Tournai-Famenian oil deposits in the Upper Kama region. Vestnik Moskovskogo universiteta. Seriya 4: Geologiya. 2019. N 5, p. 44-52. DOI: 10.33623/0579-9406-2019-5-44-52 (in Russian).
- Martyushev D.A., Lekomtsev A.V., Kotousov A.G. Determining the openness and compressibility of natural fractures in the Logovskoye carbonate deposit. Vestnik Permskogo natsionalnogo issledovatelskogo politekhnicheskogo universiteta. Geologiya. Neftegazovoe i gornoe delo. 2015. N 16, p. 61-69. DOI: 10.15593/2224-9923/2015.16.7 (in Russian).
- Martyushev D.A. Assessing the effect of rock stress state on the permeability of carbonate reservoirs. Izvestiya Tomskogo politekhnicheskogo universiteta. Inzhiniring georesursov. 2020. Vol. 331. N 9, p. 7-17. DOI: 10.18799/24131830/2020/8/2765
- (in Russian).
- Korotenko V.A., Grachev S.I., Kushakova N.P., Mulyavin S.F. Assessing the influence of water saturation and capillary pressure gradients on the formation of the two-phase filtration zone size in a compressible low-permeability reservoir. Journal of Mining Institute. 2020. Vol. 245, p. 569-581. DOI: 10.31897/PMI.2020.5.9 (in Russian).
- Panikarovskii V.V., Panikarovskii E.V., Dubrovskii V.N. Determining the stability of rocks during the exploitation of Cenomanian deposits. Izvestiya vysshikh uchebnykh zavedenii. Neft i gaz. 2010. N 3, p. 43-47.
- Zhukov V.S. Patent N 2516392 RU. Method for determining the fracture porosity of rocks. Publ. 20.05.2014. Bul. N 8.
- Kashnikov Yu.A., Ashikhmin S.G., Shustov D.V. et al. Improving the efficiency of hydrocarbon field development based on comprehensive geomechanical investigations. Neftyanoe khozyaistvo. 2019. N 3, p. 66-69. DOI: 10.24887/0028-2448-2019-3-66-69 (in Russian).
- Rudenko V.V., Galiulin I.M. Integrating an oil field geological and technological model and ground displacement monitoring methods to ensure the safety of underlying objects. Gornyi informatsionno-analiticheskii byulleten. 2014. N 4, p. 180-184 (in Russian).
- Ryzhov A.E., Perunova T.A., Orlov D.M. Pore space structure of reservoir rocks in the Botuobinsky horizon of the Chayandinskoe field. Vesti gazovoi nauki. 2011. N 1 (6), p. 162-174 (in Russian).
- Turank K., Furmentro D., Denni A. Wave propagation and interfaces in rocks. Mekhanika gornykh porod primenitelno k problemam razvedki i dobychi nefti. Moscow: Mir, 1994, p. 176-184 (in Russian).
- Galkin S.V., Krivoshchekov S.N., Kozyrev N.D. et al. Consideration of geomechanical formation properties in the development of multilayered oil fields. Journal of Mining Institute. 2020. Vol. 244, p. 408-417. DOI 10.31897/PMI.2020.4.3 (in Russian).
- Chertov M.A., Suarez-Rivera R. Practical Laboratory Methods for Pore Volume Compressibility Characterization in Different Rock Types. 48th US Rock Mechanics. Geomechanics Symposium held (ARMA’14-7532), 1-4 June 2014, Minneapolis: CRC Press, 2014, p. 14.
- Chin L., Nagel N. Modeling of Subsidence and Reservoir Compaction under Waterflood Operations. International Journal of Geomechanics. 2004. Vol. 4. Iss. 1, p. 28-34. DOI: 10.1061/(ASCE)1532-3641(2004)4:1(28)
- Guilbot J., Smith B. 4-D constrained depth conversion for reservoir compaction estimation: Application to Ekofisk Field. The Leading Edge. 2002. Vol. 21. Iss. 3, p. 302-308. DOI: 10.1190/1.1463782
- Lewis R.W., Pao W.K.S., Makurat A. Fully coupled modeling of seabed subsidence and reservoir compaction of North Sea oil fields. Hydrogeology Journal. 2003. Vol. 11, p. 142-161. DOI: 10.1007/s10040-002-0239-z
- Mavko G., Mukerji T., Dvorkin J. The Rock Physics Handbook, Second Edition. New York: Cambridge University Press, 2009, р. 525.
- Nagel N. Compaction and subsidence issues within the petroleum industry: From Wilmington to Ekofisk and beyond. Physics and Chemistry of The Earth, Part A: Solid Earth and Geodesy. 2001. Vol. 26. Iss. 1-2, p. 3-14. DOI: 10.1016/S1464-1895(01)00015-1
- Shapiro S.A., Khizhniak G.P., Plotnikov V.V. et al. Permeability dependency on and compliant porosities: a model and some experimental examples. Journal of Geophysics and Engineering. 2015. Vol. 12. Iss. 3, p. 376-385. DOI: 10.1088/1742-2132/12/3/376
- Schutjens P, Heidug W. On the pore volume compressibility and its application as a petrophysical parameter. 9th Biennial International Conference and Exposition on Petroleum Geophysics, 16-18 February 2012, Hyderabad, India. SPG, 2012. N P-512.
- Shapiro S.A. Elastic piezosensitivity of porous and fractured rocks. Geophysics. 2003. Vol. 68. Iss. 2, p. 482-486. DOI: 10.1190/1.1567215
- Sheng Guanlong. Effect of microscale compressibility on apparent porosity and permeability in shale gas reservoirs / Sheng Guanlong, Javadpour Farzam, Su Yuliang. International Journal Heat and Mass Transfer. 2018. Vol. 120, p. 56-65. DOI: 10.1016/j.ijheatmasstransfer.2017.12.014
- Shenglai Yang. Fundamentals of Petrophysics. Second Edition. Beijing: Springer Geophysics and Petroleum Industry Press, 2017, p. 502. DOI: 10.1007/978-3-662-55029-8
- Shapiro S.A., Khizhniak G.P., Plotnikov V.V. et al. Stiff- and compliant-porosity based model of permeability – Theory and experiments: Conference Proceedings. 77th EAGE Conference and Exhibition, 1-4 June 2015, Madrid, Spain. European Association of Geoscientists & Engineers, 2015, p. 2812-2816. DOI: 10.3997/2214-4609.201412949
- Jia-Jyun Dong, Jui-Yu Hsu, Wen-Jie Wu et al. Stress-dependence of the permeability and porosity of sandstone and shale from TCDP Hole-A. International Journal of Rock Mechanics and Mining Sciences. 2010. Vol. 47. Iss. 7, p. 1141-1157. DOI: 10.1016/j.ijrmms.2010.06.019
- Sviridov V.A., Mayr S.I., Shapiro S.A. Elastic properties of two VTI shale samples as a function of uniaxial stress: Experimental results and application of the porosity-deformation approach. Geophysics. 2017. Vol. 82. Iss. 6, p. 201-210.
- Tiab D., Donaldson E.C. Petrophysics: theory and practice of measuring reservoir rock and fluid transport properties. Oxford: Gulf Professional Publishing – Elsevier, 2015, p. 918.
- Zhukov V.S., Kuzmin Yu.O. The Influence of Fracturing of the Rocks and Model Materials on P-wave Propagation Velocity: Experimental Studies. Izvestiya, Physics of the Solid Earth. 2020. Vol. 56, p. 470-480. DOI: 10.31857/S0002333720040109
- Zimmerman R.W., David E.C. Compressibility and shear compliance of spheroidal pores: Exact derivation via the Eshelby tensor, and asymptotic expressions in limiting cases. International Journal of Solids and Structures. 2011. Vol. 48. Iss. 5, p. 680-686. DOI: 10.1016/j.ijsolstr.2010.11.001
- Zimmerman R.W. Introduction to Rock Properties. The Imperial College Lectures in Petroleum Engineering. 2017. Vol. 3, p. 1-46.
- Zimmerman R.W. Pore Volume and Porosity Changes under Uniaxial Strain Conditions. Transport in Porous Media. 2017. Vol. 119, p. 481-498. DOI: 10.1007/s11242-017-0894-0
- Zoback M.D. Reservoir geomechanics. New York: Cambridge University Press. 2007, p. 505. DOI: 10.1017/CBO9780511586477
