Использование функций резонанса при оценке параметров межскважинных зон
- 1 — канд. техн. наук доцент Уфимский государственный нефтяной технический университет ▪ Orcid
- 2 — д-р техн. наук профессор Уфимский государственный нефтяной технический университет
- 3 — д-р техн. наук профессор Уфимский государственный нефтяной технический университет ▪ Orcid ▪ Elibrary ▪ Scopus ▪ ResearcherID
- 4 — д-р техн. наук профессор Уфимский государственный нефтяной технический университет ▪ Orcid
- 5 — канд. техн. наук доцент Филиал Уфимского государственного нефтяного технического университета в г. Октябрьском ▪ Orcid ▪ Elibrary ▪ Scopus ▪ ResearcherID
Аннотация
Показано, что использование силового резонанса приводит к эффекту «встряхивания» пласта с последующей разбивкой пленочной нефти и вовлечением ее в дальнейший процесс фильтрации. Впервые для нефтепромысловой геофизики обоснована концепция метода пассивной шумометрии при контроле за разработкой нефтегазовой залежи за счет измерений добротности контуров в точечных областях каналов выработки пластов (КВП) межскважинных зон. Установлено, что определение глубины модуляции реактивного параметра замещения погонной цепи КВП является решающим фактором в определении параметрического возбуждения не только для систем затухания в КВП, но и без затухания в метрологическом обеспечении анализа петрофизических свойств кернов из скважин. Показано, что на основе метода комплексных амплитуд (для тока пластовых давлений, разностей дебитов, импендансов) можно построить различные семейства резонансных кривых: амплитуды смещений (при перепаде дебитов на пьезоемкости исследуемого участка пласта), скорости (амплитуды тока пластовых давлений), ускорений (амплитуды перепада дебитов на погонной пьезоиндуктивности участка КВП). А использование прогнозируемых погонных фильтрационно-емкостных свойств продуктивного пласта при непрерывном его регулировании приводит к повышению точности проведения тампонажа в каждом последующем подцикле образования нового сегмента в траекториях КВП, что способствует более полной выработке продуктивных залежей углеводородов и повышает достоверность прогнозирования показателей разработки.
Введение
Одним из наиболее эффективных методов воздействия на пласт является заводнение продуктивных горизонтов [1-3]. Однако эффективность этого метода недостаточно высока, а в отдельных случаях может быть и отрицательной [4, 5], что является отражением широкого разнообразия залежей по геологическому строению [6, 8]. В связи с этим проведены исследования, которые относятся к области гидромеханики нефтеизвлечения с повышенными показателями выработки продуктивного пласта по контурам объемов его эксплуатационных объектов, разрабатываемых с искусственным заводнением [9-11]. При этом коэффициент извлечения нефти (КИН) пласта во многом определяется достоверностью и точностью прогнозирования его параметров [12-14]. Наиболее приемлемым для прогнозирования является метод палетки Фетковича [15] и его разновидности: методы Блассингейма, Агарвала – Гарднера, NPI и др. [16-18]. Они основаны на геолого-геофизических данных по результатам исследований дебитов и давлений в нагнетательных (НС) и добывающих (ДС) скважинах [19-21]. Нужно отметить присущие им низкие метрологические возможности текущего прогнозирования параметров пластов. Все эти методы по своим измерительным возможностям относятся к классу индикаторных, так как их приведенные погрешности превышают допустимые значения (δ > 10 %) как в стационарном, так и в нестационарном режимах извлечения углеводородов [22-24].
Для данного случая проблема прогнозирования фильтрационно-емкостных свойств (ФЕС) пласта в стационарных условиях является определимой. В то же время для рентабельно функционирующих месторождений КИН равен 0,35 [25-27]. В общем виде сущность исследований прогнозируемых параметров сводится к определению параметров волновых резонансов, наиболее показательные результаты которых получены в электротехнических, акустических и других видах систем со сосредоточенными параметрами объектов управления. Но к сложнореализуемым относятся технологические процессы, например, смежных нефтехимических производств.
Впервые российскими учеными (А.Г.Бутковский, Э.Я.Рапопорт и др.) были обоснованы направления исследования систем с распределенными параметрами. Однако результаты их моделирования касаются только доступных измерений параметров зональных участков (сегментов) объектов управления. Условия моделирования работы пласта с пространственно-распределенными координатами на основе электромеханических и гидравлических аналогий существенно нарушаются при нестационарном режиме нефтеизвлечения [28-30].
Проблемы усугубляются при моделировании работы пласта на основе более совершенных гиперболических уравнений взамен ранее используемым параболическим [31-33]. Особенно это ощущается при реализации метатехнологии добычи трудноизвлекаемых углеводородов (ТрИЗУ), когда эксплуатационный объект подвергается экстремальному регулированию [4, 16, 34]. Таким образом, адекватные результаты получаются в безразмерных величинах пласта при моделировании и решении задачи Коши за счет реализации метатехнологии ТрИЗУ. При этом условия устойчивости и качества гидромеханики нефтеизвлечения можно получить в расчетной форме на основе математического аппарата волнового резонанса [35-37].
На основе перечисленных условий целью работы устанавливается повышение достоверности и точности прогнозирования параметров удаленных межскважинных зон пласта с экстремальным регулированием функции волнового резонанса в процессе повышения КИН.
Методология
Достижение обобщенной цели для наиболее полной выработки пласта обеспечивается численным моделированием и решением двух типов задач. Первая предполагает использование при моделировании цепочечной структуры модели гидромеханики нефтевытеснения гиперболического типа [34] на основе погонных параметров гидросопротивления Rг трубки тока, пьезоиндуктивности в пьезопроводности (Lг ≡ F(η)) и пьезоемкости (Сг ≡ F(σн.ост)) в нефтенасыщенности участка пласта с дополнением среднестатистических результатов петрофизики в метрологическом обеспечении ранних и промежуточных стадий разработки нефтегазовых залежей (РНЗ).
Решение второй задачи связано с определением параметров удаленных межскважинных зон за счет применения принципа автономности, впервые реализованного при использовании новой метатехнологии добычи ТрИЗУ [38-40]. Сущность ее реализации заключается в совмещении режимов нефтевытеснения, исследований и тампонировании областей в канале выработки пласта (КВП) с выполнением условий: Рнв.мин < Рнв.ном < Рнв.макс < Рисс < Ртам < Ргидр. Эти величины представлены на рис.1 в виде поддержания пластовых давлений: Рисс - исследований; максимальных Рнв.макс, номинальных Рнв.ном и минимальных Рнв.мин величин при нефтевытеснении; Ргидр - величина давления гидроразрыва пласта.
На эпюрах Э1 и Э2 (рис.1) давление тампонирования Ртам условно не используется, так как применяется только в операциях изоляции изношенных участков КВП с величиной меньше давления гидроразрыва пласта. Давление исследования Рисс выбирается для жесткого режима работы пласта, упругий режим которого используется как режим нефтевытеснения.
Верхняя эпюра Э1 отображает условно операцию расчетного времени τисip доставки под давлением пласта Рисс порции трассирующих меток в расчетную точку i (i=1,n) контролируемой области межскважинной зоны. После этого осуществляется переход в режим нефтевытеснения под давлением Рнв.ном при расчетном времени τнвip.
На эпюре Э2 отображены практические результаты исследований точки i в КВП за время τисiпp и задержкой τtз при образовании переходных процессов. При завершении доставки порции трассирующих меток в заданную точку КВП с дожимного насосного оборудования в наземных условиях снижается поддержание пластового давления от величины Рисс до Рнв.ном.
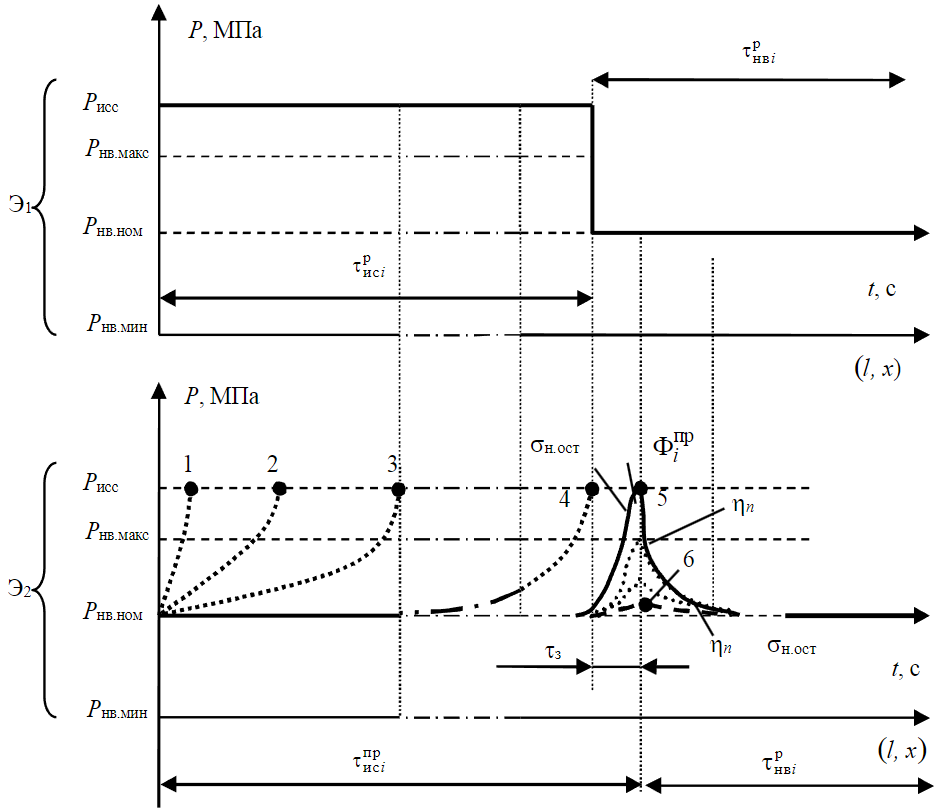
Рис.1. Временные диаграммы переходных процессов в КВП
В пластовых условиях (со стороны призабойной зоны НС) образуется серия точек 1, 2, 3 и 4 в вершинах переходных процессов. Это отображает динамику практического результата эволюционного развития одинарной i-й флуктуации Φiпр при давлениях с максимальным пятиточечным и минимальным шеститочечным значениями амплитуд. После образования переходного процесса в жестком режиме пласта (между Рисс и Рэкс.max) вначале вырабатывается флуктуация Φiпр с дальнейшим ее переходом в упругий режим, как это изображено в примере затухания изображенных амплитуд до минимально определяемой точки 6.
Для каждой флуктуации Φiпр характерно различие протяженностей (или крутизны) переднего (восходящая ветвь) и заднего (нисходящая ветвь) фронтов переходных процессов при текущем прогнозировании погонных значений остаточной нефтенасыщенности σн.ост и пьезопроводности η [15, 29, 41]. С точки зрения теории гидравлического удара такая локализация фронтов каждой флуктуации характеризуется как амплитуда сглаживания пульсаций («схлопывания») в возмущенной межскважинной области КВП при непрерывных изменениях. Все это и обуславливает определение изменяемых параметров траекторий КВП в виде погонных гидравлического сопротивления Rг, пьезопроводности Lг и пьезоемкости Сг.
Если текущие параметры стационарных процессов исследований τисip и нефтевытеснения τнвip можно прогнозировать в решениях гиперболических уравнений по цепочечной схеме КВП, то в нестационарном режиме переходных процессов пласта можно прогнозировать дополнительные параметры по локализованной схеме автономных осцилляторов.
С точки зрения электрогидромеханических аналогий для данной задачи исследований наиболее подходящим является метод комплексных амплитуд. При этом уравнение движения для осциллятора можно выразить в виде:
где P – давления в трубке линий тока разрабатываемого пласта; ∂γ – разность потенциальных дебитов жидкостей между нагнетательными и добывающими скважинами; ω – частота возбуждаемых колебаний.
При решении уравнения (1) методом комплексных амплитуд (для давления в трубке тока КВП
Р = Ре jωt) получается Р = ∂γ/Z, где Zг = Rг + j(ωLг - 1/ωCг) – комплексное сопротивление осциллятора на погонном участке КВП. Для модуля пластового давления в трубке тока пласта имеем:
Чтобы найти максимальное значение пластового давления в трубке тока пласта, должно выполняться условие Р0макс = ∂γ/R, когда ωLг= 1/ωCг (при ω = ω0).
На основании полученных условий можно найти нормированные резонансные кривые для пластового давления в виде функционала:
где P0макс – максимальное значение пластового давления; θ0 = ω0L/R – добротность резонансного контура; γ = ω/ω0 – коэффициент резонансных частот в соотношении вынужденной круговой частоты v к собственной w0 частоте резонансного контура (осциллятора) исследуемой области в удаленной зоне КВП.
На рис.2 представлено семейство нормированных резонансных кривых для пластового давления в погонной трубке тока КВП при изображении их добротностей θ0 = 1; 2; 10.
Резонанс перепадов дебитов как напряжений на пьезоемкости θ0∂γ получается при более низкой собственной частоте ω0 по отношению к круговой частоте ω. Это достигается в условиях (2) при γ2=1-1/2θ02. В отличие от этого перепад дебитов как напряжений на пьезоиндуктивности θ0∂γ получается при более высокой собственной частоте ω0 по отношению к круговой частоте ω, когда γ2=1/(1-1/2θ02).
Представленные резонансные кривые соответствуют результатам исследований изношенных областей в удаленной зоне пласта. Поэтому они получаются с однозначной симметрией резонансов для осциллятора со следующими параметрами: Lг = const; Cг = const; Rг = const; а изменяемыми являются только значения частот возбуждаемых колебаний (ω = var).
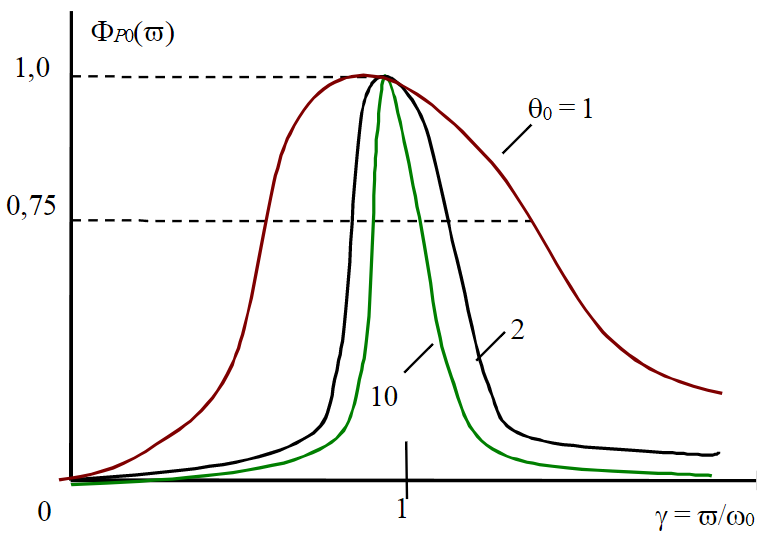
Рис.2. Интерпретация нормированных резонансных кривых для разных значений добротностей автономных осцилляторов КВП
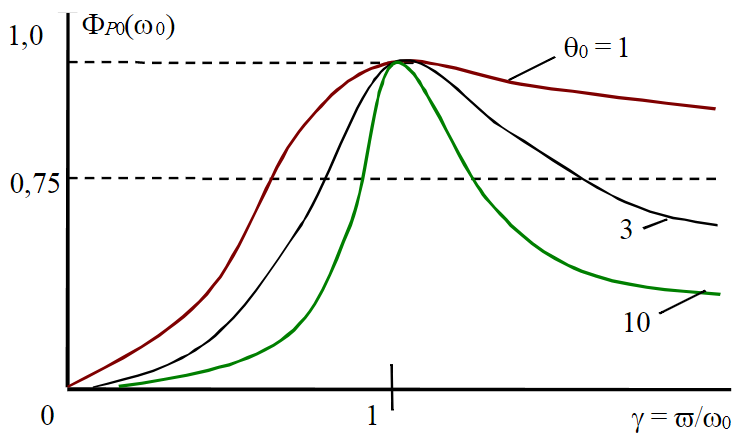
Рис.3. Семейство резонансных кривых при изменении собственной частоты автономных осцилляторов КВП для добротностей 1; 3; 10
Практический интерес вызывает определение резонансных зависимостей, когда изменяется один из энергоемких погонных параметров пьезоемкости или пьезоиндуктивности в исследуемом сегменте КВП: Lг = var (или Cг = var) при Р = const. Например, определение параметров в критической точке исследуемой области КВП за счет вычисления величин пьезопроводности. При этом нормированные резонансные кривые в виде токового функционала для пластового давления при изменении собственной частоты контура можно найти в аналогии (2):
где θ0 = ωLг/Rг – добротность резонансного контура при постоянной вынужденной частоте колебаний ω.
На рис.3 представлено семейство резонансных кривых при изменении собственной частоты автономных осцилляторов КВП для добротностей θ0 = 1; 3; 10. Таким образом, изменение одного из реактивных сопротивлений (Lг) приводит к изменению собственной частоты осциллятора ω0.
Данная задача рассматривается с точки зрения порога чувствительности оптимального нефтеизвлечения. Решение этой задачи в большей степени сводится к исследованию параметрического резонанса удаленных областей в межскважинных зонах. При этом в качестве основных расчетных величин в теории колебаний принято рассматривать значение глубины модуляции параметра пьезоемкости Cг или пьезоиндуктивности Lг в рассматриваемом случае.
По аналогии с электротехническими колебательными системами глубину модуляции пьезоемкости в функции остаточной нефтенасыщенности пласта можно определить в виде:
а глубину модуляции пьезоиндуктивности в функции пьезопроводности контролируемого удаленного участка пласта можно выразить как:
где приращение пьезоемкости ΔCг (или пьезоиндуктивности ΔLг) во много раз меньше ее номинальной величины ΔCг << C0г (или ΔLг << L0г).
Если вкладываемая энергия превосходит потери, тогда в системе происходит нарастание колебаний:
где d – логарифмический декремент затухания колебаний в контуре.
В общем виде описание параметрического резонанса для всех систем выполняется с использованием дифференциального уравнения в переменных состояниях, частным видом которого является уравнение Матье:
где y – изменения (по второй производной) состояния системы для ее характеристики в фазовой плоскости; ω20 – значения резонансной частоты системы в квадрате; m – глубина модуляции возникающего параметрического резонанса. При этом решение уравнения Матье (7) сводится к определению не только глубин модуляции m, но и областей значений соотношения частот 2ω0/ω.
Российские ученые А.А.Андронов и М.А.Леонтович рассчитали эти области значений для систем без затухания (необходимые при определении петрофизических свойств керна) и с затуханием (обеспечивающих определение погонных ФЕС КВП) на основе следующих уравнений:
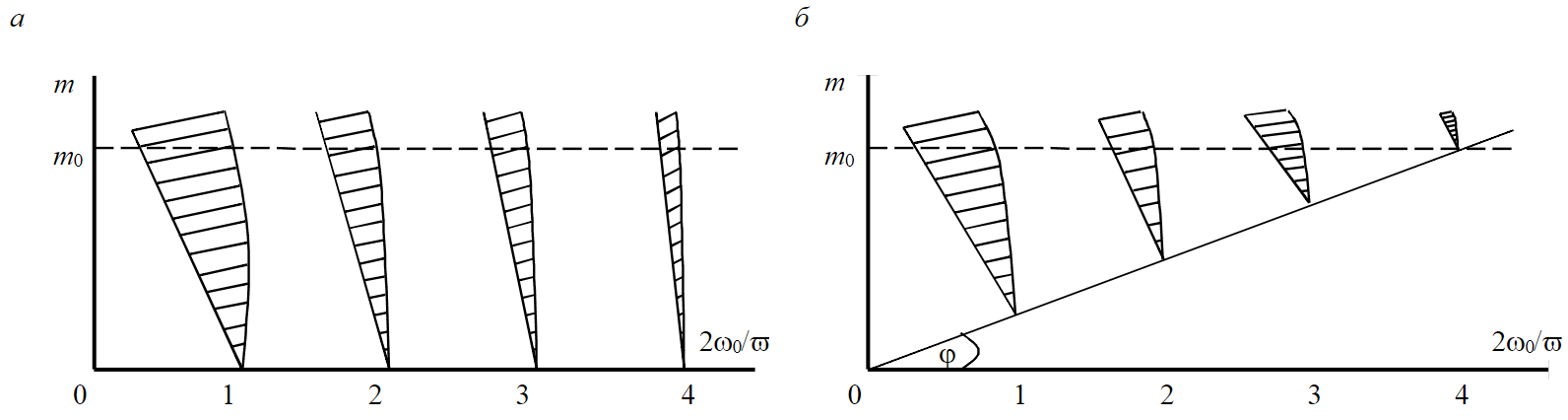
Рис.4. Области параметрического возбуждения автономных осцилляторов КВП для системы без затухания (а) и с затуханием (б)
Результаты расчетов можно пояснить в виде графиков (рис.4), где показано, что вершины областей параметрической неустойчивости поднимаются при наличии потерь в системе. В случае консервативной системы вне этих областей имеет место незатухающий сложный процесс, а в случае диссипативной – затухающий процесс колебаний. На границе областей при этом наблюдается баланс энергии.
В одних и тех же областях ширина области неустойчивости меньше у диссипативной, чем у консервативной колебательной системы. С ростом номера области неустойчивости из-за более редкого вложения энергии в систему (ω¯ = 2ω/n при n = 1, 2, 3…) для получения той же ширины области возбуждения необходимо увеличить глубину модуляции реактивного параметра m.
Таким образом, полученные значения параметрического возбуждения без затухания (рис.4, а) могут служить основой петрофизического определения волновых свойств параметров кернов при метрологическом обеспечении исследований, а с затуханием - при определении параметров исследуемых сегментов КВП. Совместное использование методов силового и параметрического резонансов обуславливает выполнение заведомо достоверного прогнозирования параметров раздельных областей межскважинных удаленных зон.
Обсуждение результатов
На поздних стадиях РНЗ величины КИН пласта обуславливаются небольшим ростом [42, 43]. Поэтому для осцилляторов в различных точках I в КВП между НС и ДС погонные параметры Rг ≃ const и Cг ≃ const. Выработанные области межскважинных зон характеризуются переменными значениями пьезопроводности, т.е. погонными пьезоиндуктивностями Lг ≃ var.
На рис.5 представлены эпюры Э1 и Э2 результатов исследований межскважинных зон в пространственной геометрии пласта (Э1) и определении величин пьезопроводностей (Э2).
Основой инструментальных средств рассматриваемых исследований является комплексная скважинная аппаратура, устанавливаемая в интервалах перфораций НС и ДС. Она состоит из скважинных преобразователей давления, температуры, расхода и обводненности нефти совместно с прибором пассивной шумометрии и гамма-аппаратурой при контроле трассирующих меток.
В результате исследований параметров КВП по схемам добротностей (см. рис.2, 3) определяются изношенные области межскважинных зон на основе методик силового резонанса с выделением областей А, В и С.
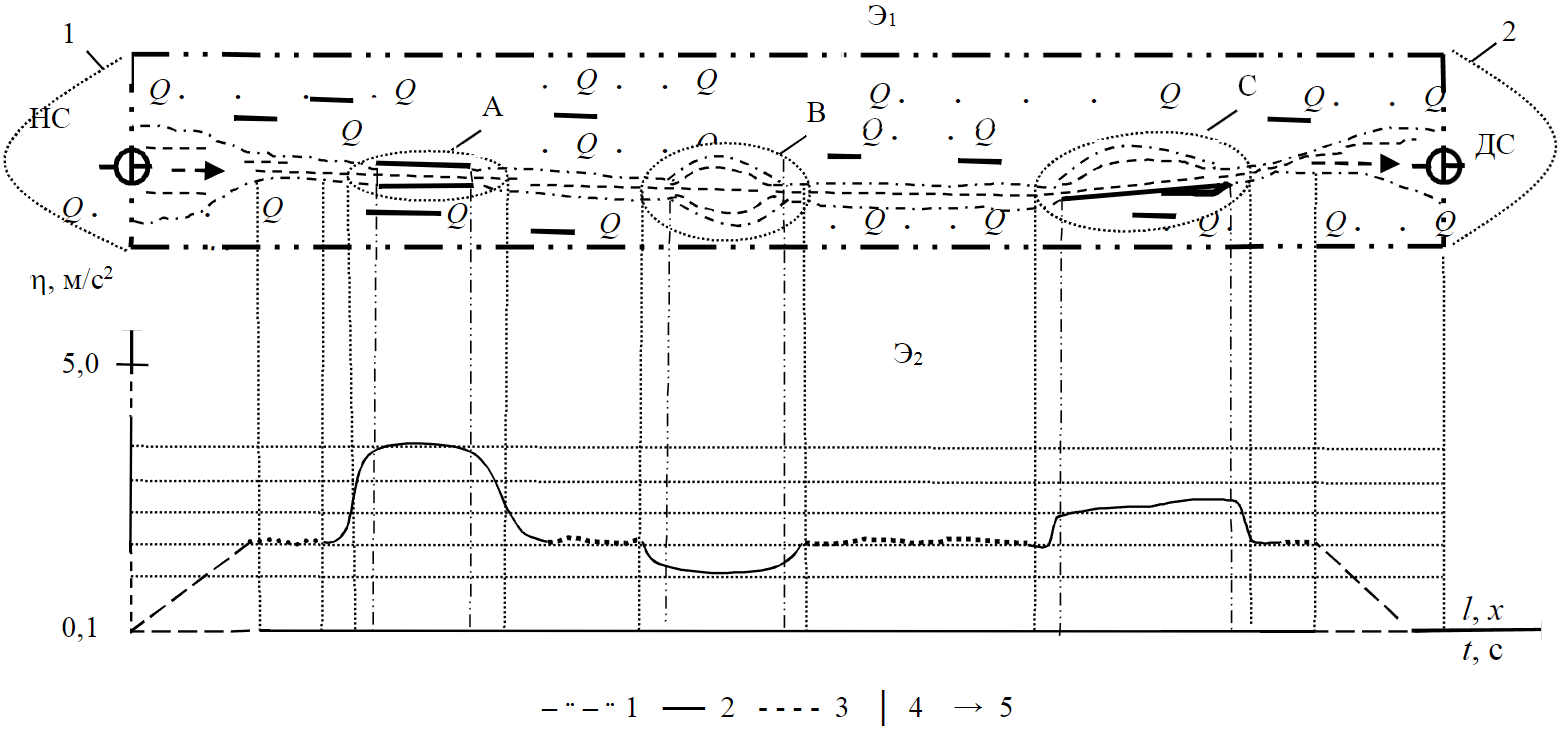
Рис.5. Эпюры результатов исследований межскважинных зон КВП (Q – остаточная нефтенасыщенность) 1 – контур эксплуатационного объекта залежи; 2 – карбонатные включения; 3 – фаза рабочего агента (воды); 4 – песчаник горной породы; 5 – направление потока флюидов
При переходе к исследованиям пласта на поздних стадиях разработки залежи в параметрическом резонансе определяются пространственно-временные координаты для определения точек тампонирования сегментов КВП в результате определения их пьезопроводностей. Исходя из этого, на эпюре Э2 выявляются области различных пьезопроводностей для определения дальнейших операций тампонирования сегментов в функционирующих траекториях l КВП.
Заключение
Использование силового резонанса приводит к эффекту «встряхивания» пласта с последующей разбивкой пленочной нефти и вовлечения ее в дальнейший процесс фильтрации. Это обуславливает необходимость контроля добротности контура в точечной области удаленной зоны КВП при возбужденном состоянии, а также дополнительной реализации условий параметрического резонанса.
Впервые для нефтепромысловой геофизики обоснована концепция метода пассивной шумометрии при контроле за РНЗ за счет измерений добротности контуров в точечных областях КВП межскважинных зон. Также впервые обоснуется использование измерений медленно меняющегося спектра амплитудно-частотной характеристики во время «схлопывания» резонансной области в исследуемой зоне.
Параметрическое возбуждение колебаний в контролируемой области КВП возможно только при изменении одного из энергоемких погонных параметров пьезоемкости Cг в функции нефтенасыщенности или пьезоиндуктивности Lг в функции пьезопроводности с терригенными, глинистыми и карбонатными породами продуктивных пластов.
Определение глубины модуляции реактивного параметра замещения погонной цепи КВП является решающим фактором в определении параметрического возбуждения не только для систем затухания в КВП, но и без затухания в метрологическом обеспечении анализа петрофизических свойств кернов.
На основе метода комплексных амплитуд (для тока пластовых давлений, разностей дебитов, импендансов) можно построить различные семейства резонансных кривых: амплитуды смещений (при перепаде дебитов на пьезоемкости исследуемого участка пласта), скорости (амплитуды тока пластовых давлений) и ускорений (амплитуды перепада дебитов на погонной пьезоиндуктивности участка КВП).
Литература
- Сергеев В.Л., Донг Ван Хоанг, Хагай Д.Э., Игнатенко А.В. Диагностические критерии выделения фильтрационных потоков в процессе гидродинамических исследований горизонтальных скважин // Известия Томского политехнического университета. Инжиниринг георесурсов. 2020. Т. 331. № 2. С. 181-187. DOI: 10.18799/24131830/2020/2/2504
- Мухаметшин В.В., Кулешова Л.С. О снижении уровня неопределенности при управлении заводнением залежей с трудноизвлекаемыми запасами // Известия Томского политехнического университета. Инжиниринг георесурсов. 2020. Т. 331. № 5. С. 140-146. DOI: 10.18799/24131830/2020/5/2644
- Яртиев А.Ф., Хакимзянов И.Н., Петров В.Н., Идиятуллина З.С. Совершенствование технологий по выработке запасов нефти из неоднородных и сложнопостроенных коллекторов Республики Татарстан. Казань: Ихлас, 2016. 191 с.
- Курбанова Г.Я., Гусева Д.Н. Применение гидродинамических методов воздействия для оптимизации системы разработки на различных стадиях заводнения // Нефть. Газ. Новации. 2015. № 12. С. 76-79.
- Van Thang Nguyen, Rogachev M.K., Aleksandrov A.N. A new approach to improving efficiency of gas-lift wells in the conditions of the formation of organic wax deposits in the dragon field // Journal of Petroleum Exploration and Production Techno-logy. 2020. Vol. 10. Iss. 8. P. 663-3672. DOI: 10.1007/s13202-020-00976-4
- Мухаметшин В.Ш., Хакимзянов И.Н. Особенности группирования низкопродуктивных залежей нефти в карбонатных коллекторах для рационального использования ресурсов в пределах Урало-Поволжья // Записки Горного института. 2021. Т. 252. С. 896-907. DOI: 10.31897/PMI.2021.6.11
- Кривощеков С.Н., Кочнев А.А., Равелев К.А. Разработка алгоритма определения технологических параметров нагнетания кислотного состава при обработке призабойной зоны пласта с учетом экономической эффективности // Записки Горного института. 2021. Т. 250. С. 587-595. DOI: 10.31897/PMI.2021.4.12
- Двойников М.В., Кучин В.Н., Минцаев М.Ш. Разработка вязкоупругих систем и технологии изоляции водоносных горизонтов с аномальными пластовыми давлениями при бурении нефтегазовых скважин // Записки Горного института. 2021. Т. 247. С. 57-65. DOI: 10.31897/PMI.2021.1.7
- Aziz K., Settari A. Petroleum Reservoir Simulation. Calgary, Alberta: Blitzprinr Lod., 2002. 477 p.
- Tongwen Jiang, Wei Yao, Xiongwei Sun et al. Evalution of anisotropic permeability of fractured sandstones subjected to true-triaxial stresses during reservoir depletion // Journal of Petroleum Science and Engineering. 2020. Vol. 200. № 108251. DOI: 10.1016/j.petrol.2020.108251
- Izotova V., Petrov D., Pankratova K., Pospehov G. Research of acoustic characteristics and physical and mechanical prope-rties of quaternary soils // Engineering and Mining Geophysics. Conference Proceedings. 2020. Vol. 2020. P.1-7. DOI: 10.3997/2214-4609.202051130
- Рогачев М.К., Мухаметшин В.В., Кулешова Л.С. Повышение эффективности использования ресурсной базы жидких углеводородов в юрских отложениях Западной Сибири // Записки Горного института. 2019. Т.240. С. 711-715. DOI: 10.31897/PMI.2019.6.711
- Мухаметшин В.В., Кулешова Л.С. Обоснование систем заводнения низкопродуктивных залежей нефти в условиях ограниченного объема информации // Научные труды НИПИ Нефтегаз ГНКАР. 2019. № 2. С. 16-22. DOI: 10.5510/OGP20190200384
- Кашников Ю.А., Ашихмин С.Г., Кухтинский А.Э., Шустов Д.В. О связи коэффициентов трещиностойкости и геофизических характеристик горных пород месторождений углеводородов // Записки Горного института. 2020. Т. 241. С. 83-90. DOI: 10.31897/PMI.2020.1.83
- Fetkovich M.J., Vienot M.E., Bradley M.D., Kiesov U.G. Decline Curve Analysis Using Type Curves – Case Histories // SPE Form Evaluation. 1987. Vol. 2. Iss. 4. P. 637-656. DOI: 10.2118/13169-PA
- Blassingeme T.A., Johnston J.L., Lee W.J. Type-Curve Analysis Using the Pressure Integral Method // SPE California Regional Meeting held, 5-7 April 1989, Hakerafieidi California. SPE 18799. P. 525-543. DOI: 10.2118/18799-MS
- Мардашов Д.В. Разработка блокирующих составов с кольматантом для глушения нефтяных скважин в условиях аномально низкого пластового давления и карбонатных пород-коллекторов // Записки Горного института. 2021. Т. 251. С. 667-677. DOI: 10.31897/PMI.2021.5.6
- Mardashov D.V., Rogachev M.K., Zeigman Yu.V., Mukhametshin V.V. Well Killing Technology before Workover Operation in Complicated Conditions // Energies. 2021. Vol. 14. Iss. 3. № 654. DOI: 10.3390/en14030654
- Захаров Л.А., Мартюшев Д.А., Пономарева И.Н. Прогнозирование динамического пластового давления методами искусственного интеллекта // Записки Горного института. 2022. Т. 253. С. 23-32. DOI: 10.31897/PMI.2022.11
- Двойников М.В., Будовская М.Е. Разработка углеводородной системы заканчивания скважин с низкими забойными температурами для условий нефтегазовых месторождений Восточной Сибири // Записки Горного института. 2022. Т. 253. С. 12-22. DOI: 10.31897/PMI.2022.4
- Григорьев Г.С., Салищев М.В., Сенчина Н.П. О применимости способа электромагнитного мониторинга гидроразрыва пласта // Записки Горного института. 2021. Т. 250. С. 492-500. DOI: 10.31897/PMI.2021.4.2
- Елесин А.В., Кадырова А.Ш., Никифирова А.И. Определение поля проницаемости пласта по замерам давления на скважинах с использованием сплайн-функции // Георесурсы. 2018. Т. 20. № 2. С. 102-107. DOI: 10.18599/grs.2018.2.102-107
- Козырев Н.Д., Вишняков А.Ю., Путилов И.С. Оценка влияния параметров неопределенности на прогнозирование показателей разработки // Недропользование. 2020. Т. 20. № 4. С. 356-368. DOI: 10.15593/2712-8008/2020.4.5
- Prischepa O.M., Borovikov I.S., Nefedov Y.V. et al. Modeling of conditions for the formation of hydrocarbon accumulation zones in the northwestern regions of the timan-pechora basin // Geomodel 2021 – 23th Conference on Oil and Gas Geological Exploration and Development, 6-10 September 2021, Gelendzhik, Russia. European Association of Geoscientists & Engineers, 2021. Vol. 2021. P. 1-5. DOI: 10.3997/2214-4609.202157097
- АндреевА.В., МухаметшинВ.Ш., КотенёвЮ.А. Прогнозирование продуктивности залежей в карбонатных коллекторах с трудноизвлекаемыми запасами // Научные труды НИПИ Нефтегаз ГНКАР. 2016. № 3. С. 40-45. DOI: 10.5510/OGP20160300287
- Mason H.E., Smith M.M., Carroll S.A. Calibration of NMR porosity to estimate permeability in carbonate reservoirs // International Journal of Greenhouse Gas Control. 2019. Vol. 87. P. 19-26. DOI: 10.1016/j.ijggc.2019.05.008
- Decheng Zhang, Ranjith P.G., Perera M.S.A., Zhang C.P. Influences of test method and loading history on permeability of tight reservoir rocks // Energy. 2020. Vol. 195. № 116902. DOI: 10.1016/j.energy.2020.116902
- Чоловский И.П., Иванова М.М., Брагин Ю.И. Нефтегазопромысловая геология залежей углеводородов. М.: Альянс, 2015. 680 с.
- Рабаев Р.У., Чибисов А.В., Котенев А.Ю. и др. Математическое моделирование растворения карбонатных коллекторов и прогнозирование эффективности регулируемой солянокислотного воздействия // SOCAR Proceedings. 2021. № 2. С. 40-46. DOI: 10.5510/OGP20210200494
- Хакимзянов И.Н., Мухаметшин В.Ш., Бахтизин Р.Н., Шешдиров Р.И. Определение объемного коэффициента сетки скважин для оценки конечного коэффициента нефтеизвлечения при разработке залежей нефти горизонтальными скважинами // SOCAR Proceedings. 2021. № 2. С. 47-53. DOI: 10.5510/OGP20210200495
- Crichlow H.B. Modern reservoir engineering – a simulation approach. New Jersey: Prentice-Hall Inc., 1977. 354 p.
- Ермеков Р.И., Меркулов В.П., Чернова О.С., Коровин М.О. Особенности учета анизотропии проницаемости в гидродинамической модели // Записки Горного института. 2020. Т. 243. С. 299-304. DOI: 10.31897/PMI.2020.3.299
- Batalov S.A., Andreev V.E., Lobankov V.M., Mukhametshin V.Sh. Numerical simulation of oil formation with regulated disturbances. Oil recovery quality simulation // Journal of Physics: Conference Series. 2019. Vol. 1333. Iss. 3. № 032006. DOI: 10.1088/1742-6596/1333/3/032006
- Batalov S.A. Modeling of the Initial Parameters in the Adjustment of an Oil Recovery Process Control System. Part 2. Determination of Limits on the Vectors of the State Variables and Disturbances // Chemical and Petroleum Engineering. Vol. 52. Iss. 7. P. 452-459. DOI: 10.1007/s10556-016-0213-6
- Бутиков Е.И. Параметрический резонанс // Компьютерные инструменты в образовании. 2009. № 3. С. 18-36.
- Зейгман Ю.В., Мухаметшин В.Ш., Хафизов А.Р., Харина С.Б. Перспективы применения многофункциональных жидкостей глушения скважин в карбонатных пластах // SOCAR Proceedings. 2016. № 3. С. 33-39. DOI: 10.5510/OGP20160300286
- Кочетков А.В., Фаттахов И.Г., Мухаметшин В.В. и др. Математическая модель линейного и нелинейного повышения концентрации пропанта при проведении ГРП – решение для последовательной закачки ряда типов пропанта // Записки Горного института. 2022. Т. 254. № 2. С. 210-216. DOI: 10.31897/PMI.2022.10
- Якупов Р.Ф., Мухаметшин В.Ш., Хакимзянов И.Н., Трофимов В.Е. Оптимизация выработки запасов из водонефтяных зон горизонта D3ps Шкаповского нефтяного месторождения с помощью горизонтальных скважин // Георесурсы. 2019. Т. 21. № 3. С. 55-61. DOI: 10.18599/grs.2019.3.55-61
- Давыдова А.Е., Щуренко А.А., Дадакин Н.М. и др. Оптимизация проведения гидродинамических исследований скважин в условиях карбонатного коллектора // Недропользование. 2018. Т. 17. № 2. С. 123-135. DOI: 10.15593/2224-9923/2018.2.3
- Pippard A. The physics of vibration. England, Cambridge: Cambridge university press, 1989. 263 p.
- Коротенко В.А., Грачёв С.И., Кушакова Н.П., Мулявин С.Ф. Оценка влияния градиентов водонасыщенности и капиллярного давления на формирование размера зоны двухфазной фильтрации в сжимаемом низкопроницаемом коллекторе // Записки Горного института. 2020. Т.245. С. 569-581. DOI: 10.31897/PMI.2020.5.9
- Мухаметшин В.В. Повышение эффективности управления объектами добычи нефти с использованием метода аналогий // SOCAR Proceedings. 2020. № 4. C. 42-50. DOI: 10.5510/OGP20200400464
- Yakupov R.F., Mukhametshin V.Sh., Tyncherov K.T. Filtration model of oil coning in a bottom water-drive reservoir // Periodico Tche Quimica. 2018. Vol. 15. Iss. 30. P. 725-733.
