Расчет взаимных спектральных плотностей моментов сопротивления на рабочих органах торфяного фрезерующего агрегата

К. В. Фомин

doi:10.31897/PMI.2021.5.14

Том 251

Страницы:

745-756

Скачать том:

RUS ENG

Научная статья

Геотехнология и инженерная геология

Расчет взаимных спектральных плотностей моментов сопротивления на рабочих органах торфяного фрезерующего агрегата

Авторы:

К. В. Фомин

Об авторах

д-р техн. наук доцент Тверской государственный технический университет ▪ Orcid

Дата отправки:

2021-04-19

Дата принятия:

2021-10-18

Дата публикации:

2021-10-29

Аннотация

При выполнении технологических операций в торфяной промышленности используются различные агрегаты с рабочими органами фрезерного типа. Они отличаются конструкцией, схемой расположения, количеством и типом режущих элементов, режимами работы, могут иметь один или несколько рабочих органов. При эксплуатации на фрезы действуют случайные силы и моменты, которые имеют резко переменный характер, что связано с периодическим взаимодействием ножей с торфяной залежью, ее структурной неоднородностью, вариацией глубины фрезерования, физико-механических свойств торфа, числа оборотов фрезы и скорости перемещения машины. При этом в элементах конструкции возникают значительные динамические нагрузки, что приводит к снижению их надежности, ухудшению энергетических характеристик работы двигателя и технико-экономических показателей использования. В случае применения машин с несколькими рабочими органами при динамическом анализе элементов привода необходимо знать как спектральные, так и взаимные спектральные плотности нагрузок. Для их расчета получены выражения, которые учитывают физико-механические свойства торфа, режимы работы агрегата и их вероятностные характеристики, а также конструктивные особенности рабочего органа. Выражения получены для случая, когда имеется несколько рабочих органов с одинаковыми диаметрами и числом ножей в плоскости резания. При этом количество плоскостей, ширина, тип режущего элемента и вид резания (блокированное, полублокированное и т.п.) могут различаться. В качестве примера использования разработанных подходов представлен расчет спектральных и взаимных спектральных плотностей моментов на фрезах и нагрузок в элементах привода машины поверхностно-послойного фрезерования МТФ-14.

Ключевые слова:

торфяной фрезерующий агрегат фреза динамические нагрузки момент сопротивления модель взаимная спектральная плотность

10.31897/PMI.2021.5.14

Введение

При выполнении технологических операций на различных стадиях добычи торфяной продукции широко используются фрезерующие агрегаты [7, 28]. В процессе их эксплуатации в элементах конструкции возникают значительные динамические нагрузки, что приводит к снижению надежности [2, 3], ухудшению энергетических характеристик работы машин и их технико-экономических показателей.

Основная причина возникновения нагрузок – силы внешнего сопротивления на рабочих органах, которые носят резко переменный и случайный характер [13, 17]. Это связано с периодическим взаимодействием режущих элементов с залежью, ее структурной неоднородностью [8, 27], случайной изменчивостью режимов работы [15] и физико-механических свойств торфа [9]. Также характер нагружения зависит от конструкции и количества фрез, их параметров и режимов работы, износа резцов, колебаний, связанных с силами резания и дисбалансом рабочих органов и т.д. [1].

Учитывая случайный характер нагрузок на режущих элементах, анализ динамических нагрузок в элементах конструкции фрезерующего агрегата и расчет показателей его надежности [4, 5] должен основываться на методах теории вероятности [23] и статистической динамики механических систем [24, 25]. Опыт их применения [12, 21, 22, 30] показывает, что на практике можно ограничиться рассмотрением только одномерных и двумерных характеристик процессов при решении данных задач с использованием как аналитических и численных методов, так и 3D-моделирования [26, 32]. При этом в расчет принимают вероятностные характеристики силовых факторов, такие как дисперсии и спектральные плотности. В [17, 18] систематизированы модели моментов на рабочих органах фрезерующих агрегатов, а также рассмотрены методики расчета их вероятностных характеристик.

Рис.1. Схема взаимодействия рабочих органов фрезерующего агрегата с торфяной залежью

Если в составе агрегата есть несколько фрез, при динамическом анализе необходимо знать также и взаимные спектральные плотности внешних нагрузок. При их определении широкое применение нашли методы статистического (имитационного) моделирования. Они универсальны, но требуют больших затрат машинного времени при расчете вероятностных характеристик нагрузок, особенно при выборе оптимальных режимов работы и конструктивных параметров фрезерующего агрегата.

Экспериментальные исследования нагрузок в элементах конструкции фрезерующих агрегатов с использованием средств тензометрирования [20] дают оценки математического ожидания, дисперсии, корреляционных функций, спектральных плотностей, плотностей распределения моментов и сил, а также характеристики их взаимной статистической связи.

Данный подход требует больших затрат времени и финансовых средств. При этом полученная информация характеризует нагруженность машины только в заданных конкретных условиях испытаний.

В [14] разработан аналитический метод расчета взаимных спектральных плотностей моментов на рабочих органах. Были рассмотрены торфяные машины с несколькими фрезами, имеющими одинаковый тип режущих элементов и ширину, которые работают в одинаковых условиях. При этом не учитывались многие расчетные случаи, часто встречающиеся в проектировании.

Повышение надежности, экономических и эксплуатационных показателей работы торфяных фрезерующих агрегатов является актуальной задачей [10, 16]. Ее решение связано с возможностью прогнозирования характера и величины действующих нагрузок в элементах конструкции [11] на основе учета специфики формирования моментов на рабочих органах и их вероятностных характеристик на стадии проектирования.

Целью статьи является разработка выражений для расчета взаимных спектральных плотностей на основе моделей формирования моментов сопротивления на фрезах торфяных машин, учитывающих их конструкцию, режимы работы и вероятностные характеристики условий эксплуатации.

Методология

Рассмотрен фрезерующий агрегат с несколькими рабочими органами (рис.1), каждый из которых имеет одинаковые радиусы расположения режущих элементов, среднюю глубину фрезерования, число ножей в плоскости резания, размещенных равномерно. В отличие от моделей, рассмотренных в [14], количество плоскостей резания, ширина резцов, расстояние между ними, их тип и условия работы, определяемые видом взаимодействия с торфяной залежью (блокированное, полублокированное), могут различаться. Фрезы также имеют разные схемы расстановки режущих элементов.

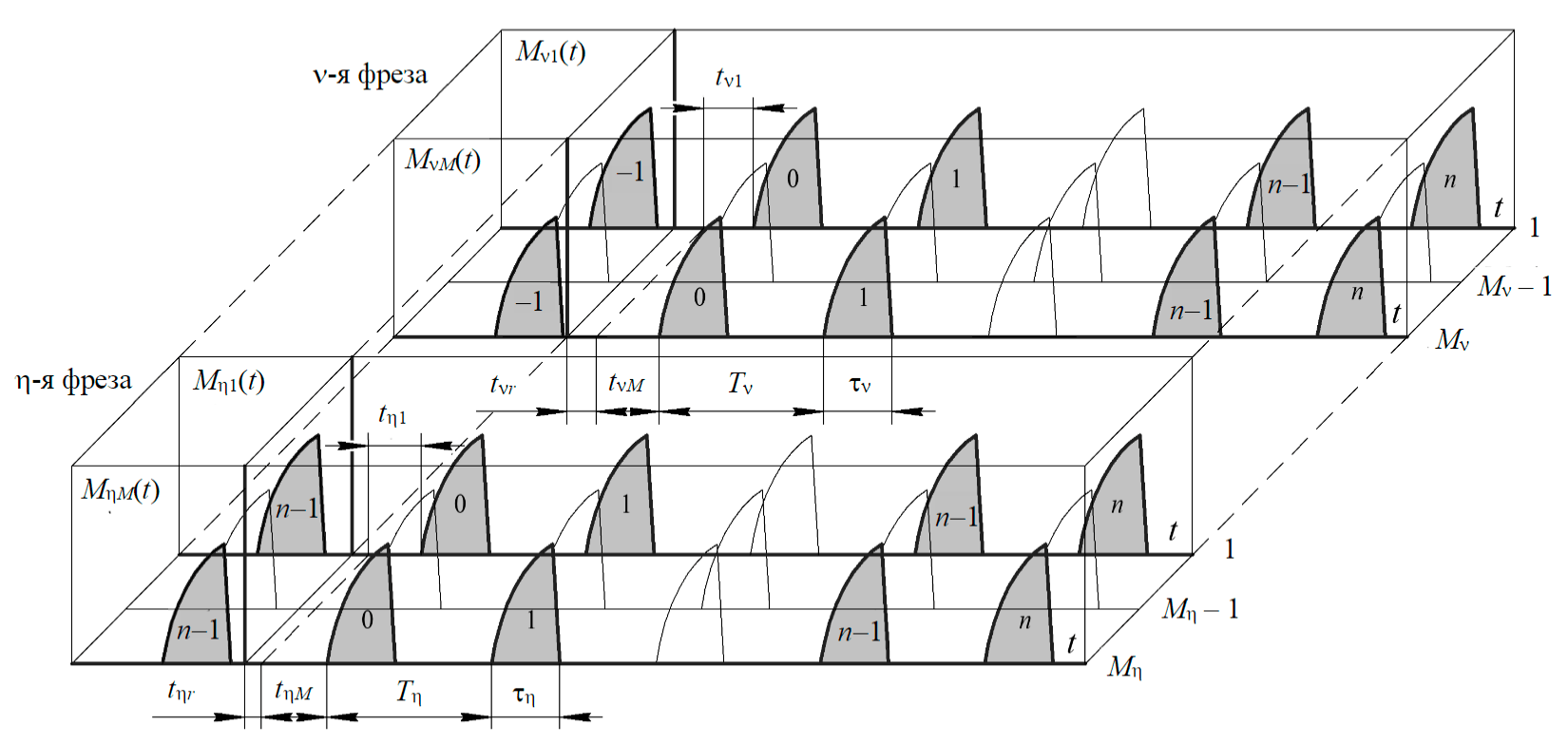
Рис.2. Модель формирования моментов сопротивления на фрезах

Учитывая существующие конструкции фрез и их режимы работы, можно считать, что скорость агрегата, число оборотов рабочего органа, глубина фрезерования и физико-механические свойства торфа изменяются плавно (в пределах нескольких подач на нож) [17]. Модели моментов сопротивления можно представить в виде импульсных процессов со случайными параметрами (рис.2):

$$ \begin{cases}M_{1po}(t)=\underset{m=1}{\overset{M_1}{\sum}}\underset{m=-\infty}{\overset{\infty}{\sum}}k_{1m}M_{mn}(t-t_{1mn}-t_{1r};P_{1mn})\\ M_{vpo}(t)=\underset{m=1}{\overset{M_v}{\sum}}\underset{m=-\infty}{\overset{\infty}{\sum}}k_{vm}M_{mn}(t-t_{vmn}-t_{vr};P_{vmn})\\ M_{ηpo}(t)=\underset{m=1}{\overset{M_η}{\sum}}\underset{m=-\infty}{\overset{\infty}{\sum}}k_{ηm}M_{mn}(t-t_{ηmn}-t_{ηr};P_{ηmn})\\ M_{Kpo}(t)=\underset{m=1}{\overset{M_K}{\sum}}\underset{m=-\infty}{\overset{\infty}{\sum}}k_{Km}M_{mn}(t-t_{Kmn}-t_{Kr};P_{Kmn})\end{cases}, \qquad(1) $$

где M_v,M_η – число плоскостей резания на n-й и η-й фрезах; k_vm, k_ηm – коэффициенты, учитывающие особенность взаимодействия (блокированное, полублокированное и т.д.), тип и ширину ножа в m-й плоскости для n-го и η-го рабочих органов; M_mn(t) – момент нагружения без учета коэффициента, зависящего от вида взаимодействия m-й плоскости при n-м акте взаимодействия; t_vmn, t_ηmn – время между началом отсчета и возникновением n-го импульса на m-й плоскости для n-го и η-го рабочих органов; P_vmn, P_η_mn – параметры импульсов на m-й плоскости резания для n-й и η-й фрез; t_vr, t_ηr – сдвиг по времени между ножами на n-м, η-м фрезах; K – число фрез.

Взаимные спектральные плотности случайных стационарных процессов являются комплексными функциями. Они связаны с взаимными энергетическими спектрами [23]:

\begin{array}{l} S_{ν η} (ω) = F_{ν η} (ω) - 2 π m_{ν} m_{η} δ (ω); \\ S_{η ν} (ω) = F_{η ν} (ω) - 2 π m_{η} m_{ν} δ (ω), \end{array}

где δ(ω) – дельта-функция; F_vη(ω), F_η_v(ω) – взаимные энергетические спектры процессов, которые могут быть определены (учитывая, что моменты сопротивления представляют собой импульсные последовательности со случайными параметрами) как [23]:

F_{ν η} (ω) = \underset{N \to \infty}{l i m} \frac{2}{(2 N + 1) T} m_{1} \{Z_{ν}^{(k)} (- j ω) Z_{η}^{(k)} (j ω)\}; (2)

F_{η ν} (ω) = \underset{N \to \infty}{l i m} \frac{2}{(2 N + 1) T} m_{1} \{Z_{η}^{(k)} (- j ω) Z_{ν}^{(k)} (j ω)\}, (3)

T – математическое ожидание периода следования импульсов; 2N + 1 – число импульсов; m₁ $\{\quad\}$ – знак усреднения; $Z^{(k)}_v(j\mathrmω)$,$Z^{(k)}_\mathrmη(j\mathrmω)$ – преобразования Фурье k-х реализаций моментов на n-м и h-м рабочих органах; m_v, m_η – математические ожидания ν-го и η-го процессов [23].

Для спектров моментов (1), содержащих (2N + 1) импульсов на v-м и η-м рабочих органах, получим:

Z_{M ν m n} (j ω) = \sum_{m = 1}^{M_{ν}} \sum_{n = - N}^{N} k_{ν m} S_{0 ν} (j ω; ω_{ф}; P_{ν m n}) e x p (- j \frac{ω}{ω_{ф}} ϕ_{ν m}) e x p (- j \frac{ω}{ω_{ф}} n ϕ_{T}) e x p (- j \frac{ω}{ω_{ф}} ϕ_{ν r}); (4)

Z_{M η m n} (j ω) = \sum_{m = 1}^{M_{η}} \sum_{n = - N}^{N} k_{η m} S_{0 η} (j ω; ω_{ф}; P_{η m n}) e x p (- j \frac{ω}{ω_{ф}} ϕ_{η m}) e x p (- j \frac{ω}{ω_{ф}} n ϕ_{T}) e x p (- j \frac{ω}{ω_{ф}} ϕ_{η r}), (5)

где S_0v(jω;ω_ф;P_vmn), S_0η(jω;ω_ф;P_η_mn) – спектры моментов M_nm(t); φ_vm, φ_η_m– углы между началами отсчета для n-й, η-й фрез (каждая фреза может иметь свою систему отсчета) и резцами в m-й плоскости для соответствующих рабочих органов; φ_T – угол между ножами в плоскости резания (равномерная расстановка резцо0в в плоскости); ω_ф – угловая скорость фрезы; φ_vr, φ_ηr – углы между резцами на n-м и η-м рабочих органах относительно начала отсчета, соответственно угол сдвига между ножами на n-й и η-й фрезах составляет φ_{ηvr =}φ_{ηr -}φ_vr (см. рис.1);

\begin{array}{l} S_{0 ν} (j ω; ω_{ф}; P_{ν m n}) = \int_{0}^{ϕ_{ν k} / ω_{ф}} M_{ν m n} (ω_{ф} t; P_{ν m n}) e x p (- j ω t) d t; \\ S_{0 η} (j ω; ω_{ф}; P_{η m n}) = \int_{0}^{ϕ_{η k} / ω_{ф}} M_{η m n} (ω_{ф} t; P_{η m n}) e x p (- j ω t) d t, \end{array}

φ_vk, φ_η_k – углы контакта ножей n-го и η-го рабочего органа с залежью.

Углы контакта φ_vk и φ_η_k являются случайными и зависят от конструкции рабочего органа, его угловой скорости, профиля поверхности карты, глубины фрезерования и колебаний, вызванных силами резания и дисбалансом фрезы.

Учитывая, что взаимные спектральные плотности S_v_η(ω) и S_η_v(ω) являются комплексно-сопряженными величинами, достаточно рассмотреть только одну из них.

Используя подходы, представленные в [14, 17], подставляя (4), (5) в (2), (3) и учитывая стационарность условий работы агрегата (вероятностные характеристики параметров импульсов не зависят от выбора начала координат), для взаимных спектральных плотностей моментов на n-й и η-й фрезах при постоянном значении угловой скорости фрез получим:

\begin{matrix} F_{ν η} (ω) = \frac{2}{T} [\sum_{q < s} {[\frac{\partial^{2} G_{1 ν η} (ω; ω_{ф}; P)}{\partial P_{q} \partial P_{s}}]}_{m} \sum_{m = 1}^{M_{ν}} \sum_{l = 1}^{M_{η}} k_{ν m} k_{η l} K_{q s ν η m l} e x p [- j \frac{ω}{ω_{ф}} (ϕ_{ν m} - ϕ_{η l})] + \\ + 2 \sum_{q < s} {[\frac{\partial^{2} G_{2 ν η} (ω; ω_{ф}; P)}{\partial P_{q} \partial P_{s}}]}_{m} \sum_{m = 1}^{M_{ν}} \sum_{l = 1}^{M_{η}} \sum_{p = 1}^{\infty} k_{ν m} k_{η l} K_{q s ν η m l p} e x p [- j \frac{ω}{ω_{ф}} (ϕ_{ν m} - ϕ_{η l})] c o s (\frac{ω}{ω_{ф}} ϕ_{T} p) + \\ + (G_{2 ν η} (ω; m_{q}) + \frac{1}{2} \sum_{q = 1}^{Q} {[\frac{\partial^{2} G_{2 ν η} (ω; ω_{ф}; P)}{\partial P_{q}^{2}}]}_{m} D_{q}) \sum_{m = 1}^{M_{ν}} \sum_{l = 1}^{M_{η}} k_{ν m} k_{η l} e x p [- j \frac{ω}{ω_{ф}} (ϕ_{ν m} - ϕ_{η l})] \times \\ \times \frac{2 π ω_{ф}}{ϕ_{T}} \sum_{k = - \infty}^{\infty} δ (ω - \frac{2 π k ω_{ф}}{ϕ_{T}})] e x p [j \frac{ω}{ω_{ф}} (ϕ_{ν r} - ϕ_{η r})], (6) \end{matrix}

где K_qsvηml, K_qsvηmlp – взаимные корреляционные моменты параметров импульсов для m-й и l-й плоскостей резания ν-го и η-го рабочих органов; m_q, D_q – математические ожидания и дисперсии параметров; p – разность номеров двух импульсов (в направлении движения агрегата), p=n-i.

В случае стационарности параметров и плавности их изменения K_qsvηml и K_qsvηmlpопределяются корреляционными функциями условий работы (прочностных свойств материала, его плотности и глубины фрезерования) в моменты взаимодействия ножей с торфяной залежью:

\begin{matrix} K_{q s ν η m l} = K_{P y} (L_{η ν} + h_{ν m} - h_{η l}); \\ K_{q s ν η m l p} = K_{P x y} (c p; L_{η ν} + h_{ν m} - h_{η l}), \end{matrix}

где m, l – номера соответствующих плоскостей резания; K_Py – корреляционные функции случайных параметров в направлении перпендикулярном движению агрегата; K_Pxy – корреляционные функции случайных параметров, учитывающие пространственную изменчивость параметров (как в направлении движения, так и перпендикулярно ему); x, y – координаты точки для соответствующих параметров; с – подача на режущий элемент; L_ηv – расстояние между η-й и ν-й фрезами (рис.1); h_vm – расстояние от торца ν-го рабочего органа до m-й плоскости резания; h_ηl – расстояние от торца η-й фрезы до l-й плоскости.

При равномерной расстановке режущих элементов по длине рабочих органов получим:

\begin{matrix} K_{q s ν η m l} = K_{P y} (L_{η ν} + (m - l) h); \\ K_{q s ν η m l p} = K_{P x y} [c p; L_{η ν} + (m - l) h], \end{matrix}

где h – расстояние между ножами в соседних плоскостях резания.

В (6) введены значения:

\begin{matrix} G_{ν η 1} (j ω; ω_{ф}; P) = S_{0 ν} (j ω; ω_{ф}; P_{ν m}) S_{0 η}^{*} (j ω; ω_{ф}; P_{η l}); \\ G_{ν η 2} (j ω; ω_{ф}; P) = S_{0 ν} (j ω; ω_{ф}; P_{ν m n}) S_{0 η}^{*} (j ω; ω_{ф}; P_{η l i}), \end{matrix}

где * – комплексно-сопряженная величина спектра.

Усредняя (6) по угловой скорости рабочего органа из

F_{C} (ω) = \int_{- \infty}^{\infty} F (ω; ω_{ф}) ​ W (ω_{ф}) d ω_{ф},

где W(ω_ф) – плотность распределения , и учитывая, что

a δ (x - x_{0}) = δ (\frac{x - x_{0}}{a}), \int_{- \infty}^{\infty} f (x) (a x - x_{0}) d x = \frac{1}{|a|} f (\frac{x_{0}}{a}),

для совместных (взаимных) энергетических спектров моментов на фрезах, получим:

\begin{matrix} F_{C ν η} (ω) = \frac{2}{T} [\sum_{q < s} \sum_{m = 1}^{M_{ν}} \sum_{l = 1}^{M_{η}} k_{ν m} k_{η l} Ψ_{1 ν η m l} K_{q s ν η m l} + 2 \sum_{q < s} \sum_{m = 1}^{M_{ν}} \sum_{l = 1}^{M_{η}} \sum_{p = 1}^{\infty} k_{ν m} k_{η l} Ψ_{2 q s ν η m l p} K_{q s ν η m l p} + \\ + \sum_{k = - \infty}^{\infty} [G_{2 ν η} (\frac{2 π k}{ϕ_{T}}; m_{q}) + \frac{1}{2} \sum_{q = 1}^{Q} {[\frac{\partial^{2} G_{2 ν η} (2 π k / ϕ_{T}; P)}{\partial P_{q}^{2}}]}_{m} D_{q}] \times \\ \times \sum_{m = 1}^{M_{ν}} \sum_{l = 1}^{M_{η}} k_{ν m} k_{η l} e x p [- j \frac{2 π k}{ϕ_{T}} (ϕ_{ν m} - ϕ_{η l})] e x p [j \frac{2 π k}{ϕ_{T}} (ϕ_{ν r} - ϕ_{η r})] \frac{ω ϕ_{T}}{2 π k^{2}} W (\frac{ω ϕ_{T}}{2 π k})], (7) \end{matrix}

T – средний период следования импульсов в плоскости резания,

\begin{matrix} T = \frac{ϕ_{T}}{\int_{- \infty}^{\infty} ω_{ф} W (ω_{ф}) d ω_{ф}}; \\ Ψ_{1 ν η m l} = \int_{- \infty}^{\infty} {[\frac{\partial^{2} G_{1 ν η} (ω; ω_{ф}; P)}{\partial P_{q} \partial P_{s}}]}_{m} e x p [- j \frac{ω}{ω_{ф}} (ϕ_{ν m} - ϕ_{η l})] e x p [j \frac{ω}{ω_{ф}} (ϕ_{ν r} - ϕ_{η r})] W (ω_{ф}) d ω_{ф}; \\ Ψ_{2 q s ν η m l p} = \int_{- \infty}^{\infty} {[\frac{\partial^{2} G_{2 ν η} (ω; ω_{ф}; P)}{\partial P_{q} \partial P_{s}}]}_{m} e x p [- j \frac{ω}{ω_{ф}} (ϕ_{ν m} - ϕ_{η l})] \times \\ \times e x p [j \frac{ω}{ω_{ф}} (ϕ_{ν r} - ϕ_{η r})] c o s (\frac{ω}{ω_{ф}} ϕ_{T} p) W (ω_{ф}) d ω_{ф} . \end{matrix}

При k_m= 1 формула (7) имеет вид, полученный в работе [14].

Рис.3. Действительные части взаимных спектральных плотностей моментов на рабочих органах (расчет) 1 – для соседних центральных фрез; 2 – для соседних средних фрез; 3 – для соседних центральной и средней фрез

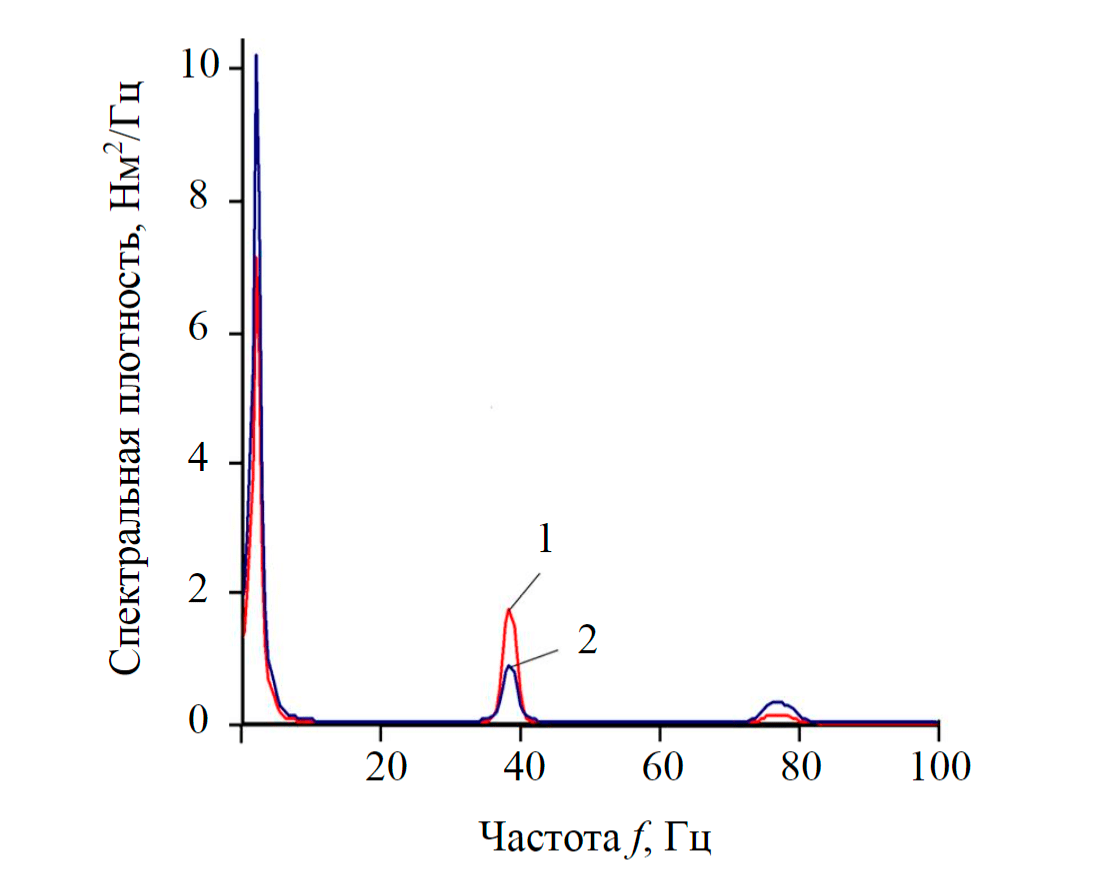
Рис.4. Спектральные плотности моментов на фрезах МТФ-14 при взаимодействии с торфом (расчет) 1 – центральная фреза; 2 – крайняя фреза

Зависимости по определению вероятностных характеристик нагрузок позволяют выделить ряд их особенностей. Взаимные спектральные плотности имеют сложную структуру и две характерные зоны частот.

Первая часть (А на рис.3) пропорциональна корреляционным функциям параметров импульсов нагружения как в направлении движения агрегата, так и перпендикулярном ему. Вид зависит от спектров моментов сопротивления на резцах различных рабочих органов S_0v(jω;ω_ф;P_v_m), S_0η(jω;ω_ф;P_ηl) и схемы их расстановки, влияние которой определяется функцией:

\sum_{m = 1}^{M_{ν}} \sum_{l = 1}^{M_{η}} k_{ν m} k_{η l} e x p [- j \frac{2 π k}{ϕ_{T}} (ϕ_{ν m} - ϕ_{η l})] .

Частоты этой части сосредоточены в низкочастотной зоне. Это объясняется плавным изменением параметров импульсов нагрузки на ноже в пределах нескольких актов взаимодействия при резании торфяной залежи и небольшой скоростью передвижения агрегата.

Вторая часть (B на рис.3) обусловлена периодическим характером взаимодействия резцов с торфом. Величина ее зависит от квадрата математических ожиданий параметров импульсов и представляет собой последовательность пиков, которые лежат на частотах w_k = 2pk/T (k = 1, 2, 3, ...). Их форма определяется функцией, описывающей плотность распределения угловой скорости фрезы, спектрами моментов S_0v(jω;ω_ф;P_v_m), S_0η(jω;ω_ф;P_ηl) и схемой расстановки режущих элементов.

Использование вероятностных характеристик моментов на рабочих органах позволяет проанализировать динамические нагрузки в элементах конструкции торфяного фрезерующего агрегата на стадии проектирования с помощью методов статистической динамики механических систем [31].

Обсуждение результатов

Рассмотрено использование предложенного подхода на примере анализа динамических нагрузок в системе привода машины поверхностно-послойного фрезерования МТФ-14, которая предназначена для выполнения первой технологической операции при добыче фрезерного торфа – измельчения верхнего слоя залежи.

В состав агрегата входят редуктор, рабочие органы со штифтовыми режущими элементами, опорные катки, задняя опора, прицеп и рама. В полной комплектации фрезер состоит из семи секций, снабженных распорными пружинами, которые шарнирно соединены между собой. Фрезер имеет три типа секций: центральная состоит из рамы, катка и двух фрез длиной 0,628 м; четыре внутренних и две крайних секции имеют раму, каток и рабочий орган с шириной захвата 1,275 м каждый. Расстояние между центральными фрезами – 0,12 м, а средними и крайними – 0,08 м; окружная скорость составляет 8,9 м/с. Диаметр рабочих органов – 0,221 м, и они имеют три штифта в плоскости резания, а диаметр корпуса – 0,157 м. Расстояние между плоскостями – 0,006 м, угол сдвига между резцами в соседних плоскостях составляет 24° (смещение по развертке корпуса – 0,03286 м). Углы между резцами на различных рабочих органах j_h_νr равны нулю; ножи имеют одинаковый размер и тип.

При эксплуатации в приводе МТФ-14 формируются значительные динамические нагрузки, что снижает надежность элементов его конструкции [12]. Основным источником их возбуждения являются силы, возникающие на фрезах [12].

Спектральные плотности моментов при взаимодействии рабочих органов с древесными включениями могут быть определены с помощью подходов, рассмотренных в [12, 19], а при фрезеровании торфа – на основании методики, разработанной в [17].

Взаимные спектральные плотности S_Cvη(jω) рассчитывались с помощью (7). При этом момент нагружения на одиночном резце без учета коэффициента k_vm, зависящего от характера взаимодействия, аппроксимирован в виде [12]:

$$ M_{vm}(t)\approx\begin{cases}\frac{M_{vmax}}{ϕ_1}ω_\mathrmфt \quad \mathrm{при} \quad 0≤ϕ≤ ϕ_1\\ M_{vmax}\bigl(2- \frac{1}{ϕ_1}ω_\mathrmфt\bigr)\quad \mathrm{при} \quad 0≤ϕ≤ ϕ_k\end{cases}, \qquad(8) $$

где φ₁ – угол поворота рабочего органа, соответствующий максимальному значению момента в пределах дуги контакта ножа с залежью; M_vmax – амплитудное значение импульса,

M_{ν m a x} = \frac{2 B_{ν} H_{ф}}{M_{ν}} \frac{W}{ω_{ф}} \frac{ϕ_{T}}{ϕ_{k}} [τ \frac{C_{T}}{δ^{0,4}} + \frac{γ ω_{ф}^{2} R_{ф}^{2}}{2 \cdot 10^{3}}],

B_ν – ширина ν-й фрезы; Н_ф – глубина фрезерования; W – скорость передвижения агрегата; τ – предельное напряжение сдвига торфа; C_T – эмпирический коэффициент; δ – средняя толщина стружки [19]; γ – плотность торфа в залежи; φ_k – угол контакта резца с залежью, φ_k=2φ₁,

ϕ_{k} = (a r c c o s \frac{R_{ф} - H_{ф}}{R_{ф}} + a r c s i n \frac{c}{2 R_{ф}}); (9)

R_ф – радиус рабочего органа по концам режущих элементов.

Спектр момента нагружения на одиночном резце (8) равен:

S_{0} (ω; ω_{ф}) = M_{ν m a x} \frac{4 ω_{ф} [1 - \cos (ω \frac{ϕ_{k}}{2 ω_{ф}})]}{ω^{2} ϕ_{k}} e x p (- j ω \frac{ϕ_{k}}{2 ω_{ф}}) .

Плотность распределения случайного значения угловой скорости фрез ω_ф может быть определена на основании подходов, рассмотренных в [25, 31]. Случайными параметрами являются: угол контакта ножа с залежью φ_k который зависит от глубины фрезерования H_ф (9); плотность торфа γ и предельное напряжение сдвига τ верхнего слоя торфяной залежи.

Рис.5. Приведенная к валу двигателя трактора динамическая расчетная схема привода МТФ-14: разветвленная расчетная (а) и основная редуцированная (б) схемы

Расчет проводился при следующих режимах работы и характеристиках торфяной залежи: скорость перемещения W = 1,94 м/с; частота вращения рабочих органов ω_ф = 80 с^–1; средняя глубина фрезерования – 0,015 м (дисперсия 0,25·10^–4 м); плотность торфа в залежи – 720 кг/м³ (коэффициент вариации 15 %); среднее значение предельного напряжения сдвига – 45 кПа (коэффициент вариации 15 %); число древесных включений на 1 га принято 500 шт. Его результаты представлены на рис.3 и 4.

Значения спектральных плотностей позволяют рассчитать вероятностные характеристики динамических нагрузок в трансмиссии фрезерующего агрегата. Для этого была использована линейная модель привода МТФ-14 [12], схема которой представлена на рис.5, а. В [12] для исследования динамических процессов разветвленная система (рис.5, а) была заменена двумя неразветвленными – защемленным ответвлением и основной редуцированной системой (рис.5, б) согласно методикам, представленным в [6, 29]. Параметры модели, приведенные к валу двигателя трактора, рассчитанные значения частот и относительные амплитуды колебаний показаны в табл.1 и 2.

Таблица 1

Параметры редуцированной динамической модели привода МТФ-14

Параметры	Номер элемента
Параметры	1	2	3	4	5	6	7	8	9
Моменты инерции, кг∙м²	3,85	0,0096	0,026	0,017	0,032	0,173	0,204	0,204	0,2
Жесткость, Нм/град.	0,29·10⁴	0,1·10⁵	0,108·10⁷	0,97·10⁵	0,13·10⁴	0,13·10⁴	0,13·10⁴	0,13·10⁴	–

Таблица 2

Относительные амплитуды и частоты собственных колебаний привода МТФ-14

Номерэлемента	Собственные частоты, с^–¹ (Гц)
Номерэлемента	27,17 (4,32)	76,27 (12,14)	120,48 (19,18)	149,42 (23,79)	219,07 (34,88)
1	–0,15213	0,04632	–0,03135	0,03067	–9,83819
2	–0,00298	–0,31141	0,57304	–0,87884	617,059
3	0,00402	–0,41341	0,74033	–1,23772	770,428
4	0,00406	–0,41429	0,74162	–1,12543	770,958
5	0,04512	–0,42372	0,75410	–1,13955	770,373
6	0,37606	–1,06809	1,41581	–1,56688	–183,421
7	0,67005	–0,88568	–0,65738	2,66139	34,3131
8	0,88638	0,10514	-1,23316	-2,43497	-6,38391
9	1	1	1	1	1

Спектральная плотность момента в i-м элементе без учета корреляции между отдельными собственными формами колебаний (в случае, когда система обладает малым затуханием, и собственные частоты не близки между собой) при использовании линейной модели привода может быть рассчитана следующим образом [31]:

\begin{matrix} S_{i} (ω) = {(C_{i} + β_{i} ω)}^{2} \sum_{ν = 1}^{K} \sum_{p = 1}^{P} \frac{{(a_{i p} - a_{i + 1; p})}^{2} a_{ν p}^{2} S_{ν} (ω)}{M_{p}^{2}} \frac{1}{{(ω_{p}^{2} - ω^{2})}^{2} + {(2 n_{p} ω)}^{2}} + \\ + {(C_{i} + β_{i} ω)}^{2} 2 \sum_{ν = 1}^{K - 1} \sum_{η = ν + 1}^{K} \sum_{p = 1}^{P} \frac{{(a_{i p} - a_{i + 1; p})}^{2} a_{ν p} a_{η p} R e S_{C ν η} (j ω)}{M_{p}^{2}} \frac{1}{{(ω_{p}^{2} - ω^{2} + j 2 n_{p} ω)}^{2}}, \end{matrix}

где C_i – жесткости элементов системы; β_i – коэффициенты демпфирования; K, a_vp, a_η_p – количество сосредоточенных масс, на которые действуют внешние нагрузки и их относительные амплитуды колебаний соответственно; P – число собственных частот; a_ip, a_i+1;p– относительные амплитуды масс, между которыми расположен i-й упругий элемент для соответствующей собственной частоты; ReS_Cvη(jω) – действительные части взаимных спектральных плотностей; ω_р – p-я собственная частота;

M_{p} = \sum_{n = 1}^{N} a_{n p}^{2} I_{n}; n_{p} = \frac{1}{M_{p}} \sum_{n = 1}^{N - 1} β_{n} a_{n p} a_{n + 1; p};

N – число масс динамической модели; I_n – моменты инерции масс.

Рассчитанные нормированные спектральные плотности на валу отбора мощности трактора (второй элемент модели) и определенные экспериментально (Г.Ф.Вековешников, О.А.Головина) [12] с помощью тензометрирования показаны на рис.6. Дисперсии момента, полученные при расчете и опытным путем, составляют 0,053 и 0,0515 кНм² соответственно.

Сопоставление результатов расчета вероятностных характеристик нагрузок в элементах трансмиссии МТФ-14 с экспериментальными данными подтверждает правильность принятых допущений для моделей формирования нагрузок на рабочих органах с учетом их взаимной статистической связи, которая характеризуется величиной взаимной спектральной плотности.

Заключение

При выполнении технологических операций на рабочих органах торфяных фрезерующих агрегатов действуют силы и моменты, которые имеют резкопеременный, случайный характер. Это предопределяет значительные динамические нагрузки в элементах конструкции машины, снижение ее надежности, ухудшение технико-экономических показателей.

При использовании методов статистической динамики механических систем для анализа динамических нагрузок на стадии проектирования фрезерующего агрегата с несколькими рабочими органами необходимо знать как спектральные, так и взаимные спектральные плотности моментов сопротивления.

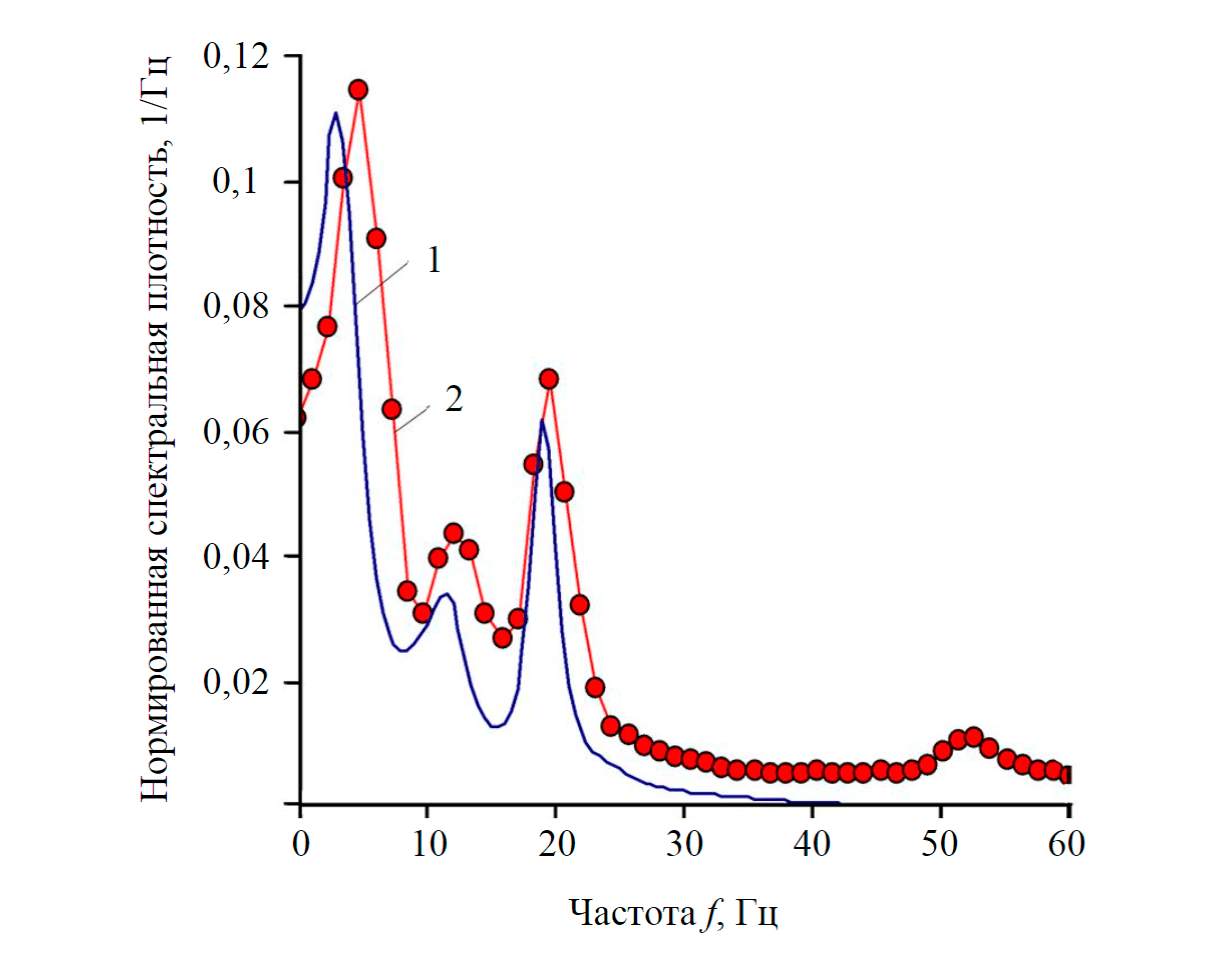
Рис.6. Нормированные спектральные плотности моментов вала отбора мощности трактора (второй элемент расчетной схемы) 1 – расчет; 2 – эксперимент [12]

На основе предложенных моделей моментов в виде импульсов со случайными параметрами получены выражения для расчета их взаимных спектральных плотностей. Они учитывают физико-механические свойства торфа, режимы работы агрегата и их вероятностные характеристики, а также конструктивные особенности рабочих органов. При этом в отличие от известных моделей, количество плоскостей резания, ширина резцов, их схема расстановки, расстояние между ножами, их тип и условия работы, определяемые видом взаимодействия с торфяной залежью (блокированное, полублокированное), на каждом из рабочих органов агрегата могут различаться.

Зависимости по определению вероятностных характеристик нагрузок позволили выделить их особенности. Взаимные спектральные плотности имеют сложную структуру и две зоны частот. Первая пропорциональна корреляционным функциям параметров импульсов нагружения, ее вид зависит от спектров моментов сопротивления на резцах и схемы их расстановки для различных рабочих органов. Вторая часть обусловлена периодическим характером взаимодействия резцов с торфом. Ее величина зависит от квадрата математических ожиданий параметров импульсов и представляет собой последовательность пиков, форма которых определяется плотностью распределения угловой скорости фрезы, а также спектрами моментов и схемой расстановки режущих элементов.

В качестве примера использования разработанных подходов и с целью оценки их достоверности представлен расчет спектральных и взаимных спектральных плотностей моментов на фрезах и нагрузок в элементах привода машины поверхностно-послойного фрезерования МТФ-14. Сравнение результатов расчета с экспериментальными данными подтверждает правильность принятых допущений для моделей формирования нагрузок на рабочих органах с учетом их взаимной статистической связи.

Взаимные спектральные плотности моментов сопротивления служат исходной информацией для расчетов динамических нагрузок в элементах конструкции торфяного фрезерующего агрегата и показателей его конструктивной надежности.

Литература

Влияние эксцентриситета рабочего органа торфяного фрезерующего агрегата на частотные свойства момента сопротивления / К.В.Фомин, К.С.Крылов, В.Е.Харламов, Н.Н.Морозихин // Труды Инсторфа. 2020. № 22 (75). С. 38-42.
Горлов И.В. Анализ параметров эксплуатации торфяной машины с помощью имитационной модели // Горный информационно-аналитический бюллетень. 2014. № 7. С. 173-177.
Горлов И.В. Влияние пнистости залежи на безотказность торфяных машин / И.В.Горлов, М.Г.Рахутин // Горный информационно-аналитический бюллетень. 2017. № 12. С. 139-145. DOI: 10.25018/0236-1493-2017-12-0-139-145
Гусев А.С. Расчет усталостной долговечности элементов конструкций при случайных процессах нагружения сложной структуры / А.С.Гусев, В.И.Щербаков, С.А.Стародубцева // Вестник машиностроения. 2015. № 12. С. 20-23.
Гусев А.С. Статистическая динамика и надежность механических систем с кинематическими, силовыми и параметрическими воздействиями / А.С.Гусев, Л.В.Зинченко, С.А.Стародубцева // Проблемы машиностроения и надежности машин. 2020. № 5. С. 21-28. DOI: 10.31857/S0235711920050065
Ефимов Л.В. Теория и практика крутильных колебаний силовых установок с применением компьютерных технологий. СПб: Наука, 2007. 276 с.
Копенкин В.Д. Развитие фрезерующих машин в торфяном производстве (анализ, перспективы) / В.Д.Копенкин, Л.В.Копенкина, Л.Н.Самсонов // Горный информационно-аналитический бюллетень. 2003. № 10. С. 204-207.
Михайлов А.В. Анализ условий вертикальной выемки торфяного сырья / А.В.Михайлов, Е.А.Родионов, И.Е.Звонарев // Горный информационно-аналитический бюллетень. 2019. № 1. С. 48-54. DOI: 10.25018/0236-1493-2019-01-0-48-54
Михайлов А.В. Особенности процесса скоростного фрезерования торфяного массива / А.В.Михайлов, А.О.Лопатюк, Д.И.Шишлянников // Известия высших учебных заведений. Горный журнал. 2017. № 2. С. 25-32.
Панов В.В. Тенденции развития торфяной отрасли России / В.В.Панов, О.С.Мисников // Горный журнал. 2015. № 7. С. 108-112. DOI: 10.17580/gzh.2015.07.15.
Принципы построения модели технического состояния трансмиссии горной машины при ее эксплуатации / С.А.Асонов, П.В.Иванова, С.Л.Иванов, Д.И.Шишлянников // Горный информационно-аналитический бюллетень. 2017. № 3. С. 15-27.
Самсонов Л.Н. Методика анализа динамической нагруженности приводов торфяных машин послойно-поверхностного фрезерования / Л.Н.Самсонов, К.В.Фомин // Горные машины и автоматика. 2004. № 1. С. 20-24.
Самсонов Л.Н. Определение вероятностных характеристик момента нагружения на рабочем органе торфяного фрезерующего агрегата / Л.Н.Самсонов, К.В.Фомин // Известия высших учебных заведений. Горный журнал. 2003. № 3. С. 106-112.
Самсонов Л.Н. Определение взаимных спектральных плотностей нагрузок на рабочих органах торфяного фрезерующего агрегата / Л.Н.Самсонов, К.В.Фомин // Горный информационно-аналитический бюллетень. 2002. № 1. С. 223-226.
Синицын В.Ф. Компьютерное моделирование поверхности карт торфяных полей / В.Ф.Синицын,Л.В.Копенкина// Труды Инсторфа. 2019. № 19 (72). С. 18-21.
Торфяная промышленность России: итоги прошлого – взгляд в будущее / Б.Ф.Зюзин, О.С.Мисников, Л.В.Копенкина, В.В.Панов // Горный журнал. 2013. № 5. С. 73-76.
Фомин К.В. Методика оценки спектральной плотности момента сопротивления на рабочем органе торфяного фрезерующего агрегата // Записки Горного института. 2020. Т. 241. С. 58-67. DOI: 10.31897/PMI.2020.1.58
Фомин К.В. Моделирование и анализ момента нагружения на рабочем органе торфяного фрезерующего агрегата // Горный информационно-аналитический бюллетень. 2002. № 2. С. 222-226.
Штин С.М. Исследования по резанию торфа и болотной древесины // Горный информационно-аналитический бюллетень. 2012. № 6. С. 374-376.
Яблонев А.Л. Применение средств современного цифрового тензометрирования при исследовании нагруженности элементов торфяных машин / А.Л.Яблонев, Ю.В.Крутов // Горный информационно-аналитический бюллетень. 2016. № 8. С. 200-205.
Chun Sheng Liu. Shearer Load Identification of the Load Spectrum of the Pick Based on Chaotic Characteristics / Chun Sheng Liu, De Gen Li, Xiao Ping Chen // Advanced Materials Research. 2011. Vol. 199-200. P. 111-114. DOI: 10.4028/www.scientific.net/AMR.199-200.111
Gong Jianchun. Characteristic analysis of random loads on shearer drum // Mining and processing equipment. 2014. Vol. 34. Iss. 8. P. 45-48.
Howard R.M. Principles of random signal analysis and low noise design: The power spectral density and its applications. Willey, 2004. 328 p. DOI: 10.1002/0471439207
Lalanne C. Mechanical Vibration and Shock Analysis, Random Vibration (Mechanical Vibration and Shock Analysis (3rd Edition)). John Wiley & Sons, 2014. 595 p. DOI: 10.1002/9781118931127
Lutes L.D. Random vibrations: analysis of structural and mechanical systems / L.D.Lutes, S.Sarkani. Butterworth-Heinemann, 2004. 650 p.
Medolago A. A flexible multi-body model of a surface miner for analyzing the interaction between rock-cutting forces and chassis vibrations / A.Medolago, S.Melzi // International Journal of Mining Science and Technology. 2021. Vol. 31. Iss. 14. P. R713-R715. DOI: 10.1016/j.ijmst.2021.03.006
Michailov A.V. An integrated approach to strip mining of peat / A.V.Michailov, A.I.Zhigulskaya, O.M.Garmaev // International Conference on Innovations and Prospects of Development of Mining Machinery and Electrical Engineering, 24-27 April 2019, Saint Petersburg, Russian Federation. IOP Conference Series: Earth and Environmental Science, 2019. Vol. 378. № 012087. DOI: 10.1088/1755-1315/378/1/012087
Misnikov O.S. Basic technologies and equipment used for peat deposit development in foreign countries // III^rd International Innovative Mining Symposium, 3-5 October 2018, Kemerovo, Russian Federation. E3S Web Conference, 2018. Vol. 41. № 01046. DOI: 10.105/e3sconf/20184101046
Nestorides E.J. Handbook of torsional vibration. Cambridge University Press, 2011. 694 p.
Simulation and Study of Random Loads on Continuous Miner Cutting Drum / Xiao Huo Li, Xin Wei Yu, Xiao Hong Ma, Ying Bo Zhao // Advanced Materials Research. 2011. Vol. 308-310. P. 1885-1888. DOI: 10.4028/www.scientific.net/amr.308-310.1885
Svetlitsky V.A. Statistical dynamics and reliability theory for mechanical structures. Springer, 2003. 452 p. DOI: 10.1007/978-3-540-45826-5
Zhao L. Reability rescearch on shearer cutting unit based on multi-body dynamics / Zhao Li-juan, Ma Yong-zhi // Journal of China Coal Society. 2009. Vol. 34. № 9. P. 1271-1275.

Расчет взаимных спектральных плотностей моментов сопротивления на рабочих органах торфяного фрезерующего агрегата

Аннотация

Введение

Методология

Обсуждение результатов

Параметры редуцированной динамической модели привода МТФ-14

Относительные амплитуды и частоты собственных колебаний привода МТФ-14

Заключение

Литература

Похожие статьи