Экспериментальное исследование влияния горного давления на проницаемость песчаника
- 1 — канд. техн. наук доцент Санкт-Петербургский горный университет ▪ Orcid
- 2 — аспирант Санкт-Петербургский горный университет ▪ Orcid
- 3 — д-р техн. наук профессор Российский государственный университет нефти и газа (НИУ) имени И.М.Губкина ▪ Orcid
Аннотация
Представлены результаты лабораторных исследований по определению влияния эффективного напряжения на проницаемость песчаника. Во время испытания образцы подвергались ступенчатому увеличению или уменьшению эффективного напряжения (при постоянном поровом давлении) с заданным шагом. Определены значения проницаемости горных пород при различных значениях эффективного напряжения, а также установлено влияние размера зерен матрицы породы-коллектора на характер изменения коэффициента проницаемости песчаника. В ходе испытания наблюдалось уменьшение проницаемости при увеличении эффективного напряжения. Установлено, что в результате ступенчатой нагрузки/разгрузки образца песчаника исходные значения проницаемости не восстанавливались, что свидетельствует о начале образования остаточных деформаций в породе. Данный эффект необходимо учитывать при моделировании разработки месторождения, так как в процессе выработки запасов меняется эффективное напряжение, действующее на скелет породы-коллектора, что приводит к значительному изменению проницаемости горной породы. Результаты лабораторных исследований показали, что отклонение проницаемости в среднезернистых песчаниках относительно исходного значения было больше, чем в средне- и мелкозернистых. Численно оценены коэффициент чувствительности к давлению и константа материала, которые используются в эмпирических зависимостях между проницаемостью и эффективным напряжением. В то же время константа материала такую сходимость не показала, что свидетельствует о том, что значения этого параметра индивидуальны для каждой породы.
Введение
Проектирование разработки нефтяного и газового месторождения – сложный процесс, состоящий из нескольких этапов. Создание гидродинамической и геологической моделей месторождения – один из важных этапов. Адекватность модели влияет на точность и надежность прогнозов ключевых показателей, определяющих эффективность разработки нефтегазовых месторождений, полноту выработанности запасов.
Для создания гидродинамической и геологической моделей пласта необходимо провести большое количество исследовательских работ, в том числе лабораторных. Одни из основных видов исследований – фильтрационные, так как течение жидкости через поровое пространство является одним из ключевых процессов, протекающих в пласте. Движение флюидов в пористых средах зависит от многих параметров: пористость и проницаемость коллектора; градиенты давления, возникающие в пласте; пластовое давление; эффективное напряжение и т.д. [1]. Большое количество работ посвящено моделированию течения жидкости через пористую среду. Многие существующие модели базируются на уравнении Дарси [2-4].
Основная задача при выборе модели – более детально и точно описать исследуемый физический процесс, поэтому современные модели течения флюидов – это многоуровневые системы уравнений со множеством переменных, которые должны учитывать ряд факторов [5-7]:
- Параметры, учитывающие несовершенство скважины по характеру и степени вскрытия.
- Расчеты по формуле Дюпюи, которые предполагают радиальную геометрию контура питания. Как показывает практика разработки нефтяных месторождений, форма контура питания не всегда круглая. Исходя из этого факта и того, что форма контура питания является одним из факторов, влияющих на приток флюида, необходим учет его геометрии [8].
- При моделировании процесса течения жидкостей необходимо учитывать изменения проницаемости, так как это один из основных параметров, характеризующих фильтрационно-емкостные свойства пород-коллекторов и производительность скважин. На значение этого параметра влияет множество процессов, в том числе и изменение напряженно-деформированного состояния (НДС) горных пород [9-12], которое зависит от физико-механических свойств горных пород [13-15], горного и порового давлений.
Многие исследователи рассматривают изменение физико-механических свойств в различных геологических условиях [16-18]. Авторы работы [10] выполнили лабораторные исследования по изучению изменений проницаемости образцов IBS (межпластового сланца) в условиях давления и температуры, аналогичных тем, которые существуют во время операций SAGD (Steam Assisted Gravity Drainage), и отметили, что модуль Юнга зависит от температуры, в то время как коэффициент Пуассона и сжимаемость образцов IBS – нет.
Проводится ряд исследований, направленных на определение прочностных характеристик осадочных пород [19-21]. Для этого использовались собственные разработки и оборудование, которые помогли исследовать динамику деформации, ползучесть песчаника, схлопывание пор и разрушение горных пород [22-24].
В работе [9] проводились испытания образцов на одноосное сжатие и растяжение с определением коэффициента Пуассона и модуля Юнга. Образцы были разделены на две группы: из пластов, подвергшихся заводнению, и из незаводненных пластов. Результаты исследований показали, что в образцах, взятых из заводняемых пластов, значения коэффициента Пуассона возрастают при одновременном значительном снижении модуля упругости и предела прочности при одноосном сжатии и растяжении.
В работе [14] отмечается влияние насыщающего флюида на основные физико-механические свойства породы. В ходе экспериментов образцы были разделены на три группы: сухие, насыщенные нефтью и пластовой водой (3 % KCl).
Анализ проведенных исследований показал, что насыщение песчаника жидкостью приводит к снижению его прочностных характеристик. При водонасыщении наблюдается наибольшее снижение предела прочности при одноосном сжатии и растяжении. Наличие жидкости (нефти или пластовой воды) в поровом пространстве горной породы приводит к уменьшению динамического модуля упругости. Наибольшее влияние на данную характеристику оказывает наличие нефти в породе-коллекторе.
Большое количество работ посвящено выявлению влияния порового и горного давлений на НДС [25-27]. При описании зависимости порового давления и эффективного напряжения нужно учитывать вклад К.Терцаги [28]. Он предложил модель для вычисления коэффициента проницаемости глины, которая описывает влияние течения флюида и изменения НДС:
где sij – эффективное напряжение; Sij – полные напряжения; Pпор – поровое давление.
Предложенную модель Терцаги доработал М.Био и вывел зависимость между напряжением скелета горной породы и давлением флюида, который заполняет поровое пространство. Модель пороупругости Био рассмотрена во многих исследованиях [29-31]. В работах [32-34] представлен закон Био:
Большинство современных моделей течения жидкости не учитывают в полной мере механику горной породы и взаимосвязь основных параметров, характеризующих НДС, с основными фильтрационно-емкостными свойствами. Данный аспект актуален в современной нефтегазовой отрасли, так как более точная корректировка закона течения жидкости в поровом пространстве при проектировании разработки месторождения углеводородов позволит достовернее спрогнозировать технико-экономические показатели разработки.
Поскольку проницаемость – это один из основных параметров, характеризующих фильтрационно-емкостные свойства пород-коллекторов, существует необходимость установить связь между эффективным напряжением и проницаемостью горной породы.
Целью настоящего исследования является установление зависимости между эффективным напряжением и проницаемостью горной породы для точного прогнозирования параметров разработки месторождения углеводородов в зависимости от стадии. В рамках достижения цели были поставлены следующие задачи: установление зависимости проницаемости породы-коллектора от эффективного напряжения, взаимосвязи между зернистостью породы-коллектора и характером изменения проницаемости.
Методология
Большинство месторождений нефти и газа России приурочены к терригенным породам со сложными геологическими строениями, поэтому в качестве образцов использовался песчаник месторождения Западной Сибири: 1-4 – песчаник светло-серый, средне- и мелкозернистый, слабослюдистый, с глинистым цементом (плотный, крепкий, массивный); 5-6 – песчаник светло-серый, среднезернистый, слабослюдистый, с глинистым цементом (плотный, крепкий, массивный).
Перед испытанием образцы были подготовлены на камнеобрабатывающем оборудовании для обеспечения параллельности поверхностей образцов. Отклонение от параллельности измеряли индикатором, устаноленным на штативе в двух взаимно перпендикулярных направлениях; размер по диаметру должен быть не более 0,2 мм (ГОСТ 21153.8-88).
После проверки параллельности поверхностей образцов следующим этапом подготовки была очистка образцов керна, включающая в себя:
- очистку образцов от остаточной жидкости (воды, нефти и др.), что достигалось промыванием, протеканием или контактированием с различными растворителями;
- всех образцов для снижения естественного содержания влаги (каждый образец керна сушили до тех пор, пока его масса не становилась постоянной).
Последний этап подготовки включает измерение высоты, диаметра и массы каждого образца. Диаметр измеряли в трех местах по высоте образца (в середине и у торцевых поверхностей) в двух взаимно перпендикулярных направлениях. Разница диаметров для этих измерений не превышала 0,5 мм. За расчетную величину принимали среднее арифметическое результатов всех измерений (ГОСТ 21153.8-88). Всего было исследовано шесть образцов.
Для проведения эксперимента выбрана следующая методика:
- Образец испытывался в установке анализатора газопроницаемости ПИК-ПП, который позволяет определять значения проницаемости в пределах от 0,01·10−3 до 10 000 мкм2, а также задавать горное давление до 70 МПа. Принцип действия анализатора основан на законе Бойля – Мариотта, где базовая характеристика фильтрационно-емкостных свойств породы определяется по расходу газа гелия, прошедшего через испытанный образец при постоянном давлении (Pпор= 0,1 МПа). Для получения более точных результатов проницаемость в каждой точке измерялась по три раза; время испытания одного образца – 10 мин.
- Замер начального значения проницаемости k1 при 10 МПа, t = 25°C.
- Ступенчатое увеличение горного давления (с замером проницаемости на каждой ступени нагружения) с шагом в 10 до 40 МПа (максимальное значение горного давления было определено, исходя из условий залегания пород).
- При достижении критического значения горного давления ступенчато (шаг 10 МПа) снижалось боковое давление до значения 10 МПа.
- После завершения четвертого пункта образец извлекался из газоанализатора ПИК-ПП, заменялся другим, и стадии 1-4 повторялись снова.
- Для определения влияния величины горного давления на значение проницаемости горной породы были построены графики зависимости (рис.1).
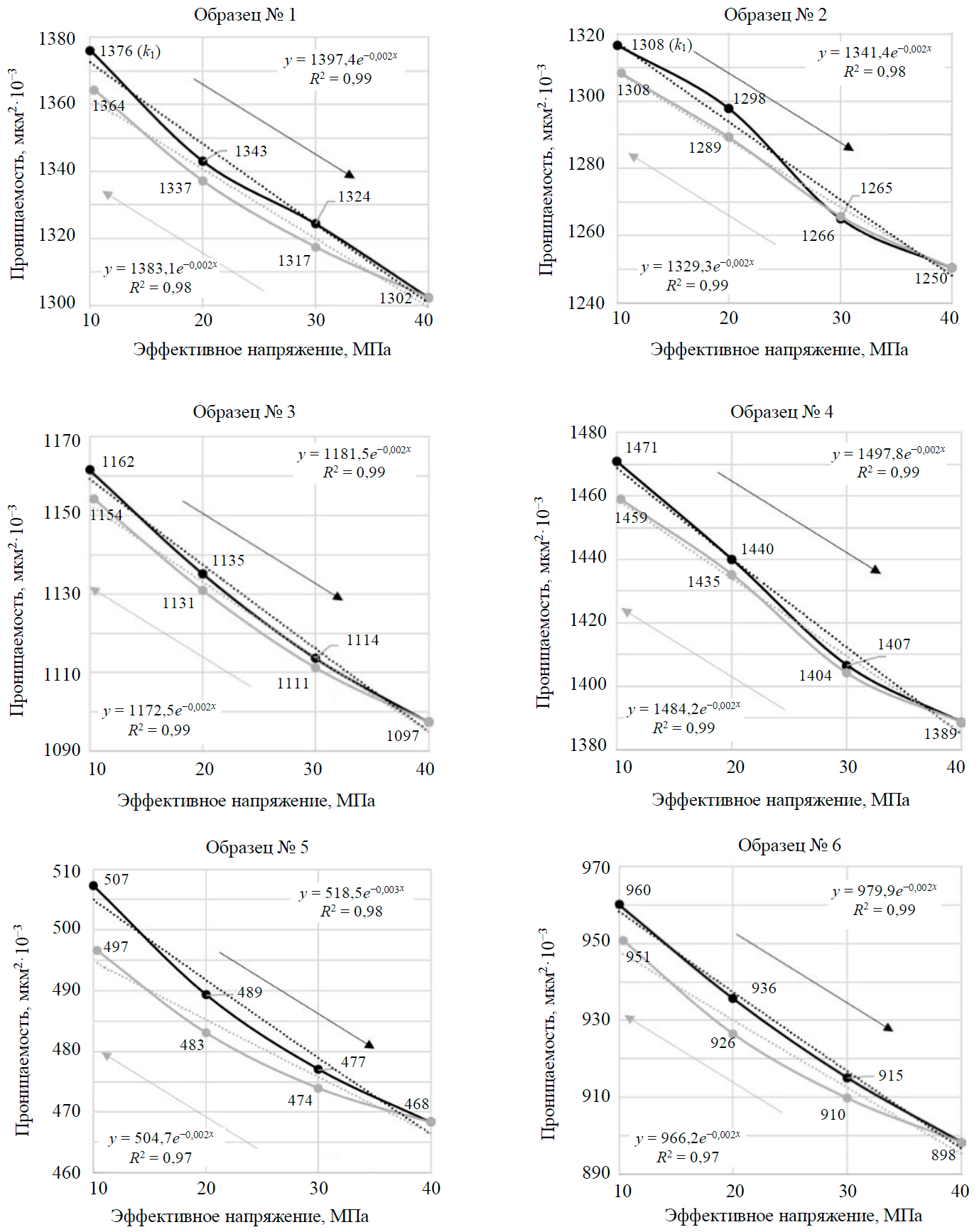
Рис.1. Зависимости изменения проницаемости от эффективного напряжения
Обсуждение результатов
Анализ результатов исследований позволил установить зависимость между одним из параметров, характеризующим эффективное напряжение, и изменением проницаемости. Эффективные напряжения σ'max, σ'min, действовавшие на образец, были меньше предельных значений, поэтому они находятся внутри круга (рис.2):
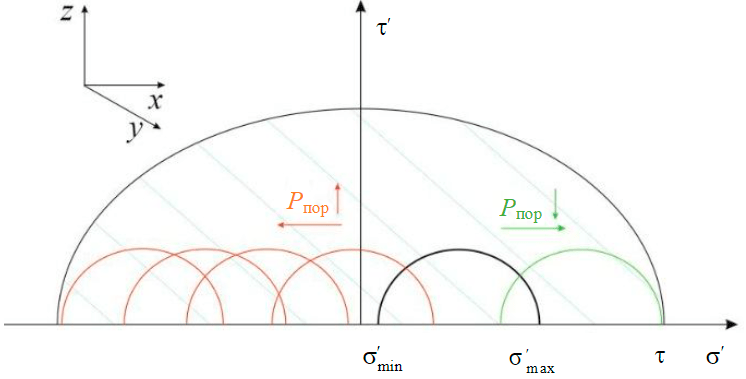
Рис.2. Схематичное представление напряженного состояния образца в ходе испытания
Результаты исследований влияния эффективного напряжения (при принятом α=1) на коэффициент проницаемости приведены на рис.1 и в табл.1.
В большинстве моделей, описывающих течение жидкости в поровом пространстве, проницаемость предполагается неизменной величиной (константой), хотя результаты этих и других исследований указывают на то, что значения проницаемости могут варьироваться в зависимости от напряжения, действующего на скелет породы. Следовательно, проницаемость является функцией напряжения. Нужно учитывать, что в зависимости от проницаемости и состава породы-коллектора влияние горного давления на значения проницаемости будет различным. В некоторых работах приводятся уравнения, устанавливающие связь между эффективным напряжением и проницаемостью породы, но существует необходимость в дополнительном определении параметра, поскольку он зависит от типа породы [35]:
где k – проницаемость при эффективном напряжении Pэфф; k0 – проницаемость при давлении P0; γ – коэффициент чувствительности к давлению.
Для определения зависимости между эффективным напряжением и проницаемостью может быть использована зависимость [36]:
где p – константа материала.
Таблица 1
Результаты исследования влияния эффективного напряжения на коэффициент проницаемости
|
Этап разгрузки |
|||||||
|
Номер образца |
Начальное |
20 МПа |
30 МПа |
40 МПа |
|||
|
Средняя |
Относительное отклонение, % |
Средняя проницаемость, мкм2·10−3 |
Относительное отклонение, % |
Средняя |
Относительное отклонение, % |
||
|
1 |
1370,36 |
1343,00 |
2,40 |
1324,38 |
3,76 |
1302,39 |
5,36 |
|
2 |
1307,11 |
1297,82 |
1,43 |
1265,12 |
3,92 |
1250,48 |
5,03 |
|
3 |
1151,39 |
1135,20 |
2,27 |
1113,65 |
4,13 |
1097,37 |
5,53 |
|
4 |
1468,22 |
1440,04 |
2,09 |
1406,66 |
4,36 |
1388,60 |
5,59 |
|
5 |
504,56 |
489,38 |
3,53 |
477,10 |
5,95 |
468,37 |
7,67 |
|
6 |
950,98 |
935,64 |
2,55 |
915,05 |
4,69 |
898,26 |
6,44 |
|
Этап нагрузки |
|||||||
|
Номер |
Начальное |
30 МПа |
20 МПа |
10 МПа |
|||
|
Средняя |
Относительное отклонение, % |
Средняя |
Относительное отклонение, % |
Средняя |
Относительное отклонение, % |
||
|
1 |
1370,36 |
1317,49 |
4,26 |
1337,15 |
2,83 |
1364,37 |
0,85 |
|
2 |
1307,11 |
1265,80 |
3,86 |
1289,34 |
2,08 |
1308,35 |
0,63 |
|
3 |
1151,39 |
1111,27 |
4,33 |
1130,96 |
2,64 |
1154,30 |
0,63 |
|
4 |
1468,22 |
1404,16 |
4,53 |
1435,29 |
2,42 |
1458,99 |
0,81 |
|
5 |
504,56 |
473,99 |
6,56 |
483,10 |
4,76 |
496,61 |
2,10 |
|
6 |
950,98 |
909,71 |
5,25 |
926,43 |
3,51 |
950,79 |
0,97 |
Согласно исследованиям, коэффициент чувствительности к давлению γ находится в интервале 1,37·10−3-18,1·10−3 МПа−1 для разных песчаников [35, 36]. Измеренные значения коэффициента чувствительности к давлению γ, приведенные в табл.2, очень близки к тем, что приводятся в [36], в то время как константа материала p отличается от представленной в данной работе.
Таблица 2
Рассчитанные параметры γ и p для образцов пород, использованных в экспериментах
|
Номер образца |
|
|
||||||
|
Нагрузка |
Разгрузка |
Нагрузка |
Разгрузка |
|||||
|
k0, мкм2·10−3 |
γ·10−3, МПа−1 |
k0, мкм2·10−3 |
γ·10−3, МПа−1 |
k0, мкм2·10−3 |
p |
k0, мкм2·10−3 |
p |
|
|
1 |
1397,39 |
1,79 |
1383,14 |
1,56 |
1505,48 |
0,039 |
1479,06 |
0,034 |
|
2 |
1341,38 |
1,80 |
1329,23 |
1,56 |
1442,47 |
0,038 |
1418,46 |
0,034 |
|
3 |
1181,48 |
1,90 |
1172,48 |
1,71 |
1278,20 |
0,041 |
1261,29 |
0,037 |
|
4 |
1497,88 |
1,96 |
1484,17 |
1,72 |
1623,99 |
0,042 |
1595,56 |
0,037 |
|
5 |
518,52 |
2,65 |
504,66 |
1,96 |
579,69 |
0,057 |
549,95 |
0,044 |
|
6 |
979,89 |
2,22 |
966,15 |
1,90 |
1073,62 |
0,047 |
1049,53 |
0,042 |
Таким образом, зависимости (5) и (6) индивидуальны для каждого месторождения. Следовательно, определение отношения эффективного напряжения к проницаемости должно выполняться на стадии опытной эксплуатации месторождения, т.е. на начальном этапе разработки нефтяного или газового месторождения, чтобы обеспечить более точное описание процессов, протекающих в коллекторе, и для точного прогнозирования основных показателей разработки.
Заключение
Проведенные исследования позволили установить зависимости между эффективным напряжением и изменением проницаемости, которые позволяют точнее прогнозировать основные показатели разработки (например, производительность скважин). Также анализ полученных зависимостей показал, что определение взаимосвязи между проницаемостью песчаника и горным давлением можно получить по следующим зависимостям:
- для средне- и мелкозернистых песчаников: k=1181,5e-0,002Pгор – при уменьшении эффективного напряжения; k=1329,2e-0,002Pгор – при увеличении эффективного напряжения;
- для среднезернистых песчаников: k= 979,9e-0,002Pгор – при уменьшении эффективного напряжения; k=966,2e-0,002Pгор – при увеличении эффективного напряжения.
Подбор оптимальных значений эффективного напряжения очень важен и актуален при определении полноты выработки запасов. Опираясь на уравнение (3), при значительном изменении порового давления (например, за счет увеличения или уменьшения давления нагнетания воды в пласт) возможно разрушение скелета породы-коллектора, что приведет к необратимому изменению проницаемости. Изменение проницаемости в каждой точке определялось относительно первоначального значения, полученного в начале испытания (k1 при Pэфф = 10 МПа). В процессе увеличения или уменьшения эффективного напряжения, действующего на образец, наблюдался гистерезис (значение проницаемости не возвращалось к своему первоначальному значению). В образцах № 1, 2 и 4 снижение проницаемости происходило неравномерно. Например, резкий скачок изменения проницаемости в образцах № 2 и 4 наблюдается в диапазоне давлений 20-30 МПа, что объясняется возможной переупаковкой порового пространства в образцах.
При гидродинамическом моделировании проницаемость должна быть функцией напряжения. Предлагаемые уравнения (5) и (6) можно использовать в качестве упрощенного соотношения для экспресс-оценки при мониторинге разработки. Но существует необходимость в дополнительном определении коэффициента чувствительности к давлению γ и константы материала p, поскольку эти параметры индивидуальны для каждого типа породы. Несмотря на тот факт, что коэффициент чувствительности к давлению γ по результатам представленных лабораторных исследований очень близок к значениям, которые приводятся в [36], рекомендуется проведение лабораторных исследований керна, чтобы выявить величины данного параметра для конкретного типа материала.
Характер изменения коэффициента проницаемости песчаника при изменении НДС зависит от размера зерен скелета, типа и состава цементирующего вещества. При снижении эффективного напряжения первоначальные показатели проницаемости образца не восстанавливаются, что свидетельствует о начале образования остаточных деформаций породы. Как показано на рис.1, среднезернистые песчаники подвергаются более сильной необратимой деформации, чем средне- и мелкозернистые. Для среднезернистых песчаников диапазон проницаемости составляет 0,97-2,1 %, для средне- и мелкозернистых – 0,63-0,85 %.
Литература
- Fan M., McClure J., Han Y. et al. Using an experiment/simulation-integrated approach to investigate fracture-conductivity evolution and non-Darcy flow in a proppant-supported hydraulic fracture // SPE Journal. 2019. Vol. Iss. 4. P. 1912-1928. DOI: 10.2118/195588-PA
- Грачев С.И., Коротенко В.А., Кушакова Н.П. Исследование влияния трансформации двухфазной фильтрации на формирование зон невыработанных запасов нефти // Записки Горного института. 2020. Т. C. 68-82. DOI: 10.31897/PMI.2020.1.68
- Гасумов Р.А. Причины отсутствия притоков пластовых флюидов при освоении скважин малых месторождений (на примере хадум-баталпашинского горизонта) // Записки Горного института. 2018. Т. С. 630-636. DOI: 10.31897/PMI.2018.6.630
- Rogatchev M.K., Sukhikh A.S., Kuznetsova A.N. Filtration tests of surfactant solutions effects on displacement efficiency oil from low-permeable polymictic reservoirs // Topical Issues of Rational use of Natural Resources-Proceedings of the International Forum-Contest of Young Researchers, 18-20 April 2018, St. Petersburg, Russia. CRC Press, 2018. P. 125-130.
- Рогов Е.А. Исследование проницаемости призабойной зоны скважин при воздействии технологическими жидкостями // Записки Горного института. 2020. Т. C. 169-173. DOI: 10.31897/PMI.2020.2.169
- Lushpeev V.A., Khmelenko P.P., Tsiku Iu.K., Tananykhin D.S. Development of smart well units for multilayer reservoirs operated with the system of simultaneous-separate exploitation // Journal of Applied Engineering Science. 2018. Vol. 16. № 4. P. 561-564. DOI: 10.5937/jaes16-17676
- Rovnik N.A., Lushpeev V.A., Tananykhin D.S., Shpurov I.V. Rational gas inflow restriction technologies during the development // Topical Issues of Rational Use of Natural Resources. 2019. Vol. 2. P. 888-900.
- Chen K.P. Production from a fractured well with finite fracture conductivity in a closed reservoir: an exact analytical solution for pseudosteady-state flow // SPE Journal. 2016. Vol. 21. Iss. 2. P. 550-556. DOI: 2118/179739-PA
- Zhao B., Zhang G., Bai X. et al. The Effects of Long-Term Waterflooding on the Physical and Mechanical Properties of Tight Sandstones // 52nd US Rock Mechanics/Geomechanics Symposium, June 2018, Seattle, Washington. OnePetro, 2018. № ARMA-2018-409.
- Oldakowski K., Sawatzky R.P. Measurements of Permeability Change in Inter-Bedded Shale at Elevated Temperatures // SPE Canada Heavy Oil Technical Conference, 15-16 February 2017, Calgary, Alberta, Canada. OnePetro, 2017. № SPE-185004-MS. DOI: 10.2118/185004-MS
- Penkov G.M., Karmansky D.A., Petrakov D.G. Simulation of a fluid influx in complex reservoirs of Western Siberia // Proceedings of the International Forum-Contest of Young Researchers «Topical Issues of Rational Use of Natural Resources»,
- -20 April 2018, St. Petersburg, Russia. CRC Press, 2019. Vol. 1. P. 119-124.
- Карасев М.А., Тиен Тай Нгуен. Метод прогноза напряженного состояния обделки подземных сооружений квази-прямоугольной и арочной форм // Записки Горного института. 2022. С. 1-10 (Online first). DOI: 31897/PMI.2022.17
- Yastrebova K.N., Chernobay V.I., Moldovan D.V. Estimation of rock mass by the ultrasonic method for determining the degree of inhomogeneity // Test Engineering and Management. 2020. № 83. P. 6792-6796.
- Zhang S., Wu S., Zhang G. Three-Dimensional Strength Characteristics of Zigong Sandstone Under True Triaxial Stresses // ISRM International Symposium-10th Asian Rock Mechanics Symposium, 29 October – 3 November, Singapore. OnePetro, 2018. № ISRM-ARMS10-2018-214.
- Кашников Ю.А., Шустов Д.В., Кухтинский А.Э., Кондратьев С.А. Геомеханические характеристики терригенных продуктивных объектов нефтяных месторождений Западного Урала // Нефтяное хозяйство. 2017. Т. 2017. Вып. 4. С.32-35. DOI: 24887/0028-2448-2017-4-32-35
- Korshunov V.A., Solomoychenko D.A., Bazhukov A.A. Strength estimation of fractured rock using compression – a specimen with spherical indenters // ISRM Regional Symposium-EUROCK 2018, 22-26 May 2018, St. Petersburg, Russia. OnePetro, 2018. № ISRM-EUROCK-2018-034.
- Rozanov A.O., Petrov D.N., Rozenbaum A.M., Tereshkin A.A. Acoustic Emission Precursor Criteria of Rock Damage // ISRM Regional Symposium-EUROCK 2018, 22-26 May 2018, St. Petersburg, Russia. OnePetro, 2018. № ISRM-EUROCK-2018-090.
- Ильинов М.Д., Карташов Ю.М. Ускоренный метод определения реологических свойств горных пород // Записки Горного института. Т. 190. С. 207-209.
- Jin Yu, Xu Chen, Yan-yan Cai, Hong Li. Triaxial test research on mechanical properties and permeability of sandstone with a single joint filled with gypsum // KSCE Journal of Civil Engineering. 2016. Vol. 20. Iss. 6. P. 2243-2252. DOI: 10.1007/s12205-015-1663-7
- Liu C., Yu B., Zhang D., Zhao H. Experimental study on strain behavior and permeability evolution of sandstone under constant amplitude cyclic loading‐unloading // Energy Science & Engineering. 2020. Vol. Iss. 2. P. 452-465. DOI: 10.1002/ese3.527
- Sakhaee-Pour A., Agrawal A. Predicting breakdown pressure and breakdown cycle in cyclic fracturing // SPE Production & Operations. 2018. Vol. 33. Iss. 4. P. 761-769. DOI: 10.2118/191137-PA
- Zhang D., Yang Y., Chu Y., Zhang X. Influence of loading and unloading velocity of confining pressure on strength and permeability characteristics of crystallines and stone // Results in Physics. 2018. Vol. 9. P. 1363-1370. DOI: 1016/j.rinp.2018.04.043
- Kallesten E., Andersen P., Berawala D. et al. Modeling of permeability and strain evolution in chemical creep compaction experiments with fractured and unfractured chalk cores conducted at reservoir conditions // SPE Journal. 2020. Vol. 25. Iss. 5. 2710-2728. DOI: 10.2118/197371-PA
- Nath F., Salvati P.E., Mokhtari et al. Laboratory Investigation of Dynamic Strain Development in Sandstone and Carbonate Rocks Under Diametrical Compression Using Digital-Image Correlation // SPE Journal. 2019. Vol. 24. Iss. 1. P. 254-273. DOI: 10.2118/187515-PA
- Rafieepour S., Miska S.Z., Ozbayoglu E.M. et al. Experimental Investigation of Depletion-and Injection-Induced Changes in Poromechanical, Transport, and Strength Properties of High-Porosity Sandstone // SPE Journal. 2021. Vol. 26. Iss. 5. P. 2793-2813. DOI: 10.2118/205364-PA
- Luo,Were P., Jianfeng Liu J., Hou Z. Estimation of Biot’s effective stress coefficient from well logs // Environmental earth sciences. 2015. Vol. 73. Iss. 11. P. 7019-7028. DOI: 10.1007/s12665-015-4219-8
- Qiao L.P., Wong R.C.K., Aguilera R. Kantzas A. Determination of Biot's effective-stress coefficient for permeability of Nikanassin sandstone // Journal of Canadian Petroleum Technology. 2012. Vol. 51. Iss. 03. DOI: 10.2118/150820-PA
- Terzaghi K. The shearing resistance of saturated soils and the angle between the planes of shear // First international conference on soil Mechanics. 1936. Vol. 1. P. 54-59.
- Jun He, Zhenhua Rui, Kegang Ling. A new method to determine Biot's coefficients of Bakken samples // Journal of Natural Gas Science and Engineering. 2016. Vol. 35. Part A. P. 259-264. DOI: 10.1016/j.jngse.2016.08.061
- Li Q., Aguilera R., Cinco-Ley H. A Correlation for Estimating the Biot Coefficient // SPE Drilling & Completion. 2020. Vol. 35. Iss. 2. P. 151-163. DOI: 10.2118/195359-PA
- Aldana Gallego I.C., Santos L.P., Yucel Akkutlu I. A Laboratory Method for Estimation of Storage Capacity of Rock Samples under Effective Stress // SPE Journal. 2021. Vol. 26. Iss. 6. P. 3725-3741. DOI: 10.2118/195552-PA
- Civan F. Compressibility, porosity, and permeability of shales involving stress shock and loading/unloading hysteresis // SPE Journal. 2019. Vol. 24. Iss. 6. P. 2458-2481. DOI: 2118/195676-PA
- El Faidouzi M.M. Contribution of Tidal Analysis to Reservoir Monitoring: A Field Case Study in a Fractured Reservoir Offshore Abu Dhabi, UAE // SPE Reservoir Evaluation & Engineering. 2020. Vol. 23. Iss. 4. P. 1440-1457. DOI: 10.2118/188837-PA
- Civan F. Effective-Stress Coefficients of Porous Rocks Involving Shocks and Loading/Unloading Hysteresis // SPE Journal. 2021. Vol. 26. Iss. 01. P. 44-67. DOI: 10.2118/200501-PA
- David C., Wong T., Zhu W., Zhang J. Laboratory measurement of compaction-induced permeability change in porous rocks: Implications for the generation and maintenance of pore pressure excess in the crust // Pure and Applied Geophysics. 1994. Vol. 143. Iss. 1. P. 425-456. DOI: 10.1007/BF00874337
- Dong J., Hsu J., Wu W. et al. Stress-dependence of the permeability and porosity of sandstone and shale from TCDP Hole-A // International Journal of Rock Mechanics and Mining Sciences. 2010. Vol. 47. Iss. 7. P. 1141-1157. DOI: 10.1016/j.ijrmms.2010.06.019
