Experimental study on the effect of rock pressure on sandstone permeability
- 1 — Ph.D. Associate Professor Saint Petersburg Mining University ▪ Orcid
- 2 — Postgraduate Student Saint Petersburg Mining University ▪ Orcid
- 3 — Ph.D., Dr.Sci. Professor Gubkin Russian State University of Oil and Gas ▪ Orcid
Abstract
The results of laboratory studies to determine the effect of effective stress on the permeability of sandstone are presented. During the test, the samples were subjected to a stepwise increase or decrease of the effective stress (at a constant pore pressure) in a specified step. The values of rock permeability at different values of effective stress were determined, and the influence of the grain size of the reservoir rock matrix on the character of the change in the sandstone permeability coefficient was also established. During the test, a decrease in permeability was observed with an increase in effective stress. It was found that as a result of gradual loading/unloading of the sandstone sample, the original permeability values were not restored, which indicates the beginning of the formation of residual strains in the rock. This effect should be taken into account when modeling field development because in the process of reserves extraction the effective stress acting on the reservoir rock skeleton changes, which results in a significant chang in rock permeability. The results of laboratory studies showed that the deviation of permeability in medium-grained sandstones relative to the initial value was greater than in medium- and fine-grained sandstones. The pressure sensitivity coefficient and constant of material, which are used in empirical relationships between permeability and effective stress, were numerically estimated. At the same time, the constant of material showed no such convergence, which indicates that the values of this parameter are individual for each rock.
Introduction
Designing the development of an oil and gas field is a complex process, consisting of several stages. Creating hydrodynamic and geological models of a field is one of the important stages. Model adequacy influences accuracy and reliability of predictions for key figures that determine efficiency of oil and gas fields’ development, completeness of reserves depletion.
In order to create hydrodynamic and geological model of a formation, it is necessary to carry out a large amount of research work, including laboratory investigation. One of the main types of research is filtration studies, since fluid flow through the pore space is one of the key processes occurring in the formation. Fluid movement in porous media depends on many parameters: porosity and permeability of the reservoir, pressure gradients in the formation, formation pressure, effective stress, etc. [1]. A large number of works are dedicated to the simulation of fluid flow through porous media. Many existing models are based on Darcy equation [2-4].
The main task in selecting a model is to describe the investigated physical process accurately and precisely, so modern fluid flow models are multi-level systems of equations with many variables, which have to take into account a number of factors [5-7]:
- Parameters that take into account well imperfection by nature and degree of drilling-in.
- Calculations by Dupuis formula assuming a radial feed contour geometry. As the practice of developing the oil fields shows, the shape of the feed contour is not always circular. Proceeding from this fact and the fact that the shape of the feed contour is one of the factors influencing fluid inflow, its geometry has to be taken into account [8].
- When simulating the process of fluid flow it is necessary to take into account changes in permeability, as it is one of the main parameters characterizing permeability and porosity properties of reservoir rocks and well productivity. The value of this parameter is influenced by many processes, including change of the stress-strain state (SSS) of rocks [9-12], which depends on physical and mechanical properties of rocks [13-15], rock and pore pressures.
Many researchers examine changes in physical and mechanical properties in different geological conditions [16-18]. The authors of [10] performed a laboratory study of changes in permeability of IBS (interbedded shale) samples in pressure and temperature conditions similar to those that exist during SAGD (Steam Assisted Gravity Drainage) operations and observed that Young modulus is temperature dependent, whereas Poisson coefficient and compressibility of IBS samples are not.
A number of studies have been carried out to determine the durability characteristics of sedimentary rocks [19-21]. Custom designs and equipment have been used to investigate deformation dynamics, sandstone creep, pore collapse and rock destruction [22-24].
In [9] the samples were tested for uniaxial compression and tension with the determination of Poisson coefficient and Young modulus. The samples were divided into two groups: from waterflooded and non-waterflooded formations. The research results showed that in samples taken from waterflooded formations, the values of Poisson coefficient increase with a simultaneous significant decrease in the modulus of elasticity and durability limit in uniaxial compression and tension.
Work [14] notes the effect of saturating fluid on the basic physical and mechanical properties of the rock. During the experiments, the samples were divided into three groups: dry, saturated by oil and formation water (3 % KCl).
The analysis of conducted studies has shown that fluid saturation of sandstone leads to a decrease in its durability properties. The greatest decrease in uniaxial compressive and tensile durability limit is observed with water saturation. The presence of fluid (oil or formation water) in the pore space of a rock leads to a decrease in the dynamic modulus of elasticity. Presence of oil in the reservoir rock has the greatest influence on this characteristic.
A large number of works have been devoted to identifying the effect of pore and rock pressure on the SSS [25-27]. When describing the dependence of pore pressure and effective stress, the contribution of K.Terzaghi [28] should be taken into account. He proposed a model to calculate the clay permeability coefficient, which describes the influence of fluid flow and changes in SSS:
where σij – effective stress; Sij – full stresses; Ppor – pore pressure.
The model proposed by Terzaghi was further developed by M.Biot. He derived the relationship between the rock skeleton stress and the pressure of the fluid that fills the pore space. Biot poroelasticity model has been reviewed in many works [29-31]. Biot’s law is presented in [32-34]:
Most of modern fluid flow models do not fully take into account rock mechanics and the relationship between the main parameters characterizing the SSS with the main permeability and porosity properties. This aspect is relevant in modern oil and gas industry, as more precise correction of fluid flow law in pore space when designing hydrocarbon field development will allow to predict technical and economic indicators of development more accurately.
Since permeability is one of the main parameters characterizing the permeability and porosity properties of reservoir rocks, there is a need to establish a relationship between effective stress and rock permeability.
The objective of this research is to determine the relationship between effective stress and rock permeability for accurate prediction of the parameters of hydrocarbon field development depending on the stage. In order to achieve the goal, the following tasks were set: determination of the dependence of reservoir rock permeability on effective stress, the relationship between reservoir rock granularity and the nature of permeability changes.
Methodology
Most oil and gas fields in Russia are confined to terrigenous rocks with complex geological structures, so sandstone from the West Siberian field was used as samples: 1-4 – light gray sandstone, medium- and fine-grained, weakly mica, with clay cement (dense, firm, massive); 5-6 – light gray sandstone, medium-grained, weakly mica, with clay cement (dense, firm, massive).
Before the test, the samples were prepared on stonecutting equipment to ensure parallelism of the sample surfaces. The deviation from parallelism was measured with an indicator mounted on a tripod in two mutually perpendicular directions; the diameter dimension should be no more than 0.2 mm (GOST 21153.8-88).
After checking the parallelism of the sample surfaces, the next preparation step was the cleaning of the rock samples, which included:
- cleaning of samples from residual fluid (water, oil, etc.), which was achieved by washing, leaking or contacting with various solvents;
- drying of all samples to reduce the natural moisture content (each rock sample was dried until its mass became constant).
The last preparation step involves measuring the height, diameter and mass of each sample. The diameter was measured at three locations along the height of the sample (in the middle and at the end surfaces) in two mutually perpendicular directions. The difference in diameter for these measurements did not exceed 0.5 mm. The arithmetical mean of all measurements (GOST 21153.8-88) was taken as the calculated value. Six samples were examined in total.
The following methodology was chosen for the experiment:
- The sample was tested in the gas permeability analyzer PIK-PP, which allows to determine the permeability values in the range from 0.01-10−3 to 10 000 μm2 as well as to set rock pressure up to 70 MPa. The operating principle of the analyzer is based on Boyle – Marriott law, where the basic parameter of rock permeability is determined by helium flow rate through the tested sample at constant pressure (Ppor = 0.1 MPa). To obtain more accurate results, the permeability was measured three times at each point; the test time per sample was 10 min.
- Measuring the initial permeability value k1 at 10 MPa, t = 25 °C.
- Stepwise increase in rock pressure (with permeability measurements at each loading stage) in steps of 10 to 40 MPa (maximum rock pressure value was determined based on bedding conditions).
- When the critical rock pressure was reached, the lateral pressure was reduced to 10 MPa with a step of 10 MPa.
- After completing stage 4, the sample was removed from the PIK-PP gas analyzer, replaced by another sample and stages 1-4 were repeated.
- To determine the effect of rock pressure magnitude on rock permeability, dependence plots were constructed (Fig.1).
Discussion of the results
The analysis of the research results allowed establishing a correlation between one of the parameters characterizing the effective stress and the change in permeability.
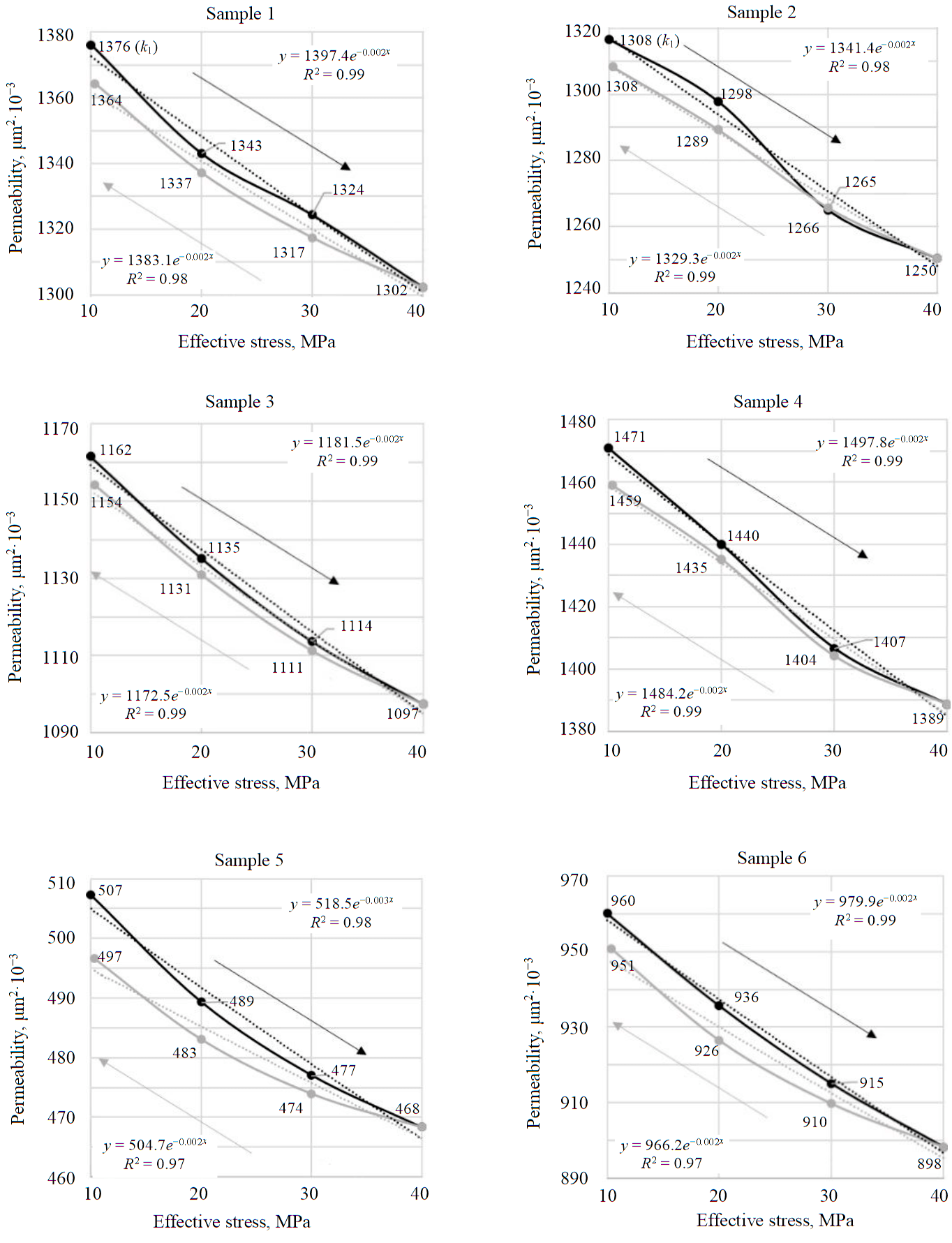
Fig.1. Dependencies of changes in permeability on effective stress
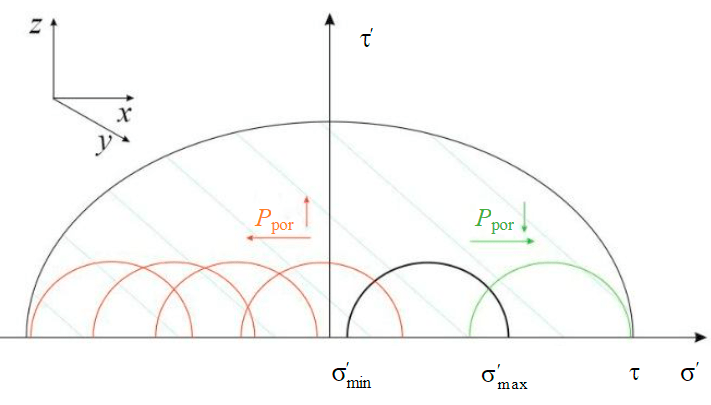
Fig.2. Schematic representation for the stress state of the sample during the test
Effective stresses σ'max, σ'min, acting on the sample were smaller than the limit values, so they are inside the circle (Fig.2):
The results of the studies on the effect of the effective stress (at the assumed α=1) on the permeability coefficient are shown in Fig.1 and Table 1.
In most models describing fluid flow in pore space, permeability is assumed to be a constant, although the results of these and other studies indicate that permeability values may vary depending on the stress acting on the rock skeleton. Consequently, permeability is a function of stress. It should be noted that depending on permeability and composition of reservoir rock, the effect of rock pressure on permeability values will vary. In some works, equations are given to establish the relationship between effective stress and rock permeability, but there is a need for additional definition of the parameter, as it depends on the type of rock [35]:
where k – permeability at effective stress Peff; k0 – permeability at pressure P0; γ – pressure sensitivity coefficient.
The dependence [36] can be used to determine the relationship between effective stress and permeability:
where p – constant of the material.
Table 1
Results of a study on the effect of effective stress on the permeability coefficient
|
Unloading stage |
|||||||
|
Sample |
Initial value k1, mD |
20 MPa |
30 MPa |
40 MPa |
|||
|
Average permeability, μm2·10−3 |
Relative deviation, % |
Average permeability, μm2·10−3 |
Relative deviation, % |
Average permeability, μm2·10−3 |
Relative deviation, % |
||
|
1 |
1370.36 |
1343.00 |
2.40 |
1324.38 |
3.76 |
1302.39 |
5.36 |
|
2 |
1307.11 |
1297.82 |
1.43 |
1265.12 |
3.92 |
1250.48 |
5.03 |
|
3 |
1151.39 |
1135.20 |
2.27 |
1113.65 |
4.13 |
1097.37 |
5.53 |
|
4 |
1468.22 |
1440.04 |
2.09 |
1406.66 |
4.36 |
1388.60 |
5.59 |
|
5 |
504.56 |
489.38 |
3.53 |
477.10 |
5.95 |
468.37 |
7.67 |
|
6 |
950.98 |
935.64 |
2.55 |
915.05 |
4.69 |
898.26 |
6.44 |
|
Loading stage |
|||||||
|
Sample |
Initial value k1, mD |
30 MPa |
20 MPa |
10 MPa |
|||
|
Average permeability, μm2·10−3 |
Relative deviation, % |
Average permeability, μm2·10−3 |
Relative deviation, % |
Average permeability, μm2·10−3 |
Relative deviation, % |
||
|
1 |
1370.36 |
1317.49 |
4.26 |
1337.15 |
2.83 |
1364.37 |
0.85 |
|
2 |
1307.11 |
1265.80 |
3.86 |
1289.34 |
2.08 |
1308.35 |
0.63 |
|
3 |
1151.39 |
1111.27 |
4.33 |
1130.96 |
2.64 |
1154.30 |
0.63 |
|
4 |
1468.22 |
1404.16 |
4.53 |
1435.29 |
2.42 |
1458.99 |
0.81 |
|
5 |
504.56 |
473.99 |
6.56 |
483.10 |
4.76 |
496.61 |
2.10 |
|
6 |
950.98 |
909.71 |
5.25 |
926.43 |
3.51 |
950.79 |
0.97 |
According to studies, the pressure sensitivity coefficient γ is in the range of 1.37·10−3-18.1·10−3 MPa−1 for different sandstones [35, 36]. The measured values of the pressure sensitivity coefficient γ given in Table 2 are very close to those given in [36], while the material constant p differs from that presented in this paper.
Table 2
Calculated parameters γ and p for the rock samples used in the experiments
|
Sample |
|
$$
|
||||||
|
Loading |
Unloading |
Loading |
Unloading |
|||||
|
k0, μm2·10−3 |
γ·10−3, MPa−1 |
k0, μm2·10−3 |
γ·10−3, MPa−1 |
k0, μm2·10−3 |
p |
k0, μm2·10−3 |
p |
|
|
1 |
1397.39 |
1.79 |
1383.14 |
1.56 |
1505.48 |
0.039 |
1479.06 |
0.034 |
|
2 |
1341.38 |
1.80 |
1329.23 |
1.56 |
1442.47 |
0.038 |
1418.46 |
0.034 |
|
3 |
1181.48 |
1.90 |
1172.48 |
1.71 |
1278.20 |
0.041 |
1261.29 |
0.037 |
|
4 |
1497.88 |
1.96 |
1484.17 |
1.72 |
1623.99 |
0.042 |
1595.56 |
0.037 |
|
5 |
518.52 |
2.65 |
504.66 |
1.96 |
579.69 |
0.057 |
549.95 |
0.044 |
|
6 |
979.89 |
2.22 |
966.15 |
1.90 |
1073.62 |
0.047 |
1049.53 |
0.042 |
Thus, dependencies (5) and (6) are individual for each field. Consequently, determination of the relationship between effective stress and permeability must be carried out at the stage of pilot field operation, that is, at the initial stage of oil or gas field development, in order to provide a more accurate description of processes occurring in the reservoir and to accurately predict the main development parameters.
Conclusion
Conducted studies allowed to establish relationships between effective stress and change in permeability, which allow more accurate prediction of key development indicators (e.g., well productivity). In addition, analysis of the obtained dependencies showed that the determination of the relationship between sandstone permeability and rock pressure can be derived from the following dependencies:
- for medium- and fine-grained sandstones: k=1181.5e-0.002Pr – when the effective stress is decreased; k=1329.2e-0.002Pr – when the effective stress is increased;
- for medium-grained sandstones: k=979.9e-0.002Pr – when the effective stress is decreased; k=966.2e-0.002Pr – when the effective stress is increased.
The selection of optimum effective stress values is very important and relevant in determining the completeness of reserves recovery. Based on equation (3), if pore pressure changes significantly (e.g., by increasing or decreasing water injection pressure), the reservoir rock skeleton may be destroyed, which will lead to irreversible permeability change. The permeability change at each point was determined relative to the initial value obtained at the beginning of the test (k1 at Peff = 10 MPa). In the process of increasing or decreasing the effective stress acting on the sample, hysteresis (permeability value did not return to its initial value) was observed. In samples 1, 2 and 4 the permeability decrease was uneven. For example, a sharp change of permeability in samples 2 and 4 is observed in the pressure range of 20-30 MPa that can be explained by possible repacking of pore space in the samples.
In hydrodynamic modelling, permeability should be a function of stress. The proposed equations (5) and (6) can be used as a simplified relationship for express estimation in development monitoring. However, there is a need for additional definition of pressure sensitivity coefficient γ and constant of material p, as these parameters are individual for each rock type. Despite the fact that the pressure sensitivity coefficient γ from the presented laboratory studies is very close to the values given in [36], it is recommended to perform laboratory rock samples tests in order to identify the values of this parameter for a specific type of material.
The nature of the change in the permeability coefficient of sandstone with changes in SSS depends on the skeleton grain size, type and composition of the cementing material. The initial permeability values of the sample do not recover when the effective stress decreases that indicates the beginning of residual deformation of the rock. As shown in fig. 1, medium-grained sandstones undergo greater irreversible deformation than medium- and fine-grained sandstones. For medium-grained sandstones, the permeability range is 0.97-2.1 %, for medium- and fine-grained sandstones it is 0.63-0.85 %.
References
- Fan M., McClure J., Han Y. et al. Using an experiment/simulation-integrated approach to investigate fracture-conductivity evolution and non-Darcy flow in a proppant-supported hydraulic fracture. SPE Journal. 2019. Vol. 24. Iss. 4, p. 1912-1928.
- DOI: 10.2118/195588-PA
- Grachev S.I., Korotenko V.A., Kushakova N.P. Study on influence of two-phase filtration transformation on formation of zones of undeveloped oil reserves. Journal of Mining Institute. 2020. Vol. 241, p. 68-82. DOI: 10.31897/PMI.2020.1.68
- Gasumov R.A. Causes of Fluid Entry Absence When Developing Wells of Small Deposits (on the example of the Khadum-Batalpashinsky horizon). Journal of Mining Institute. 2018. Vol. 234, p. 630-636. DOI: 10.31897/PMI.2018.6.630
- Rogatchev M.K., Sukhikh A.S., Kuznetsova A.N. Filtration tests of surfactant solutions effects on displacement efficiency oil from low-permeable polymictic reservoirs. Topical Issues of Rational use of Natural Resources-Proceedings of the International Forum-Contest of Young Researchers, 18-20 April 2018, St. Petersburg, Russia. CRC Press, 2018, p. 125-130.
- Rogov E.A. Study of the well near-bottomhole zone permeability during treatment by process fluids. Journal of Mining Institute. 2020. Vol. 242, p. 169-173. DOI: 10.31897/PMI.2020.2.169
- Lushpeev V.A., Khmelenko P.P., Tsiku Iu.K., Tananykhin D.S. Development of smart well units for multilayer reservoirs operated with the system of simultaneous-separate exploitation. Journal of Applied Engineering Science. 2018. Vol. 16. N 4, p. 561-564.
- DOI: 10.5937/jaes16-17676
- Rovnik N.A., Lushpeev V.A., Tananykhin D.S., Shpurov I.V. Rational gas inflow restriction technologies during the development. Topical Issues of Rational Use of Natural Resources. 2019. Vol. 2, p. 888-900.
- Chen K.P. Production from a fractured well with finite fracture conductivity in a closed reservoir: an exact analytical solution for pseudosteady-state flow. SPE Journal. 2016. Vol. 21. Iss. 2, p. 550-556. DOI: 10.2118/179739-PA
- Zhao B., Zhang G., Bai X. et al. The Effects of Long-Term Waterflooding on the Physical and Mechanical Properties of Tight Sandstones. 52nd US Rock Mechanics/Geomechanics Symposium, June 2018, Seattle, Washington. OnePetro, 2018. N ARMA-2018-409.
- Oldakowski K., Sawatzky R.P. Measurements of Permeability Change in Inter-Bedded Shale at Elevated Temperatures. SPE Canada Heavy Oil Technical Conference, 15-16 February 2017, Calgary, Alberta, Canada. OnePetro, 2017. N SPE-185004-MS.
- DOI: 10.2118/185004-MS
- Penkov G.M., Karmansky D.A., Petrakov D.G. Simulation of a fluid influx in complex reservoirs of Western Siberia. Proceedings of the International Forum-Contest of Young Researchers “Topical Issues of Rational Use of Natural Resources”, 18-20 April 2018, St. Petersburg, Russia. CRC Press, 2019. Vol. 1, p. 119-124.
- Karasev M.A., Tien Tay Nguen. Method for predicting the stress state of lining in quasi-rectangular and arch-shaped underground structures. Journal of Mining Institute. 2022, p. 1-10 (Online first). DOI: 10.31897/PMI.2022.17
- Yastrebova K.N., Chernobay V.I., Moldovan D.V. Estimation of rock mass by the ultrasonic method for determining the degree of inhomogeneity. Test Engineering and Management. 2020. N 83, p. 6792-6796.
- Zhang S., Wu S., Zhang G. Three-Dimensional Strength Characteristics of Zigong Sandstone Under True Triaxial Stresses. ISRM International Symposium-10th Asian Rock Mechanics Symposium, 29 October – 3 November, Singapore. OnePetro, 2018. N ISRM-ARMS10-2018-214.
- Kashnikov Yu.A., Shustov D.V., Kukhtinskiy A.E., Kondrat'ev S.A. Geomechanical characteristics of terrigenous productive objects of oil fields in the Western Urals. Oil industry – Neftyanoe khozyaistvo. 2017. Vol. 2017. Iss. 4, p. 32-35.
- DOI: 10.24887/0028-2448-2017-4-32-35
- Korshunov V.A., Solomoychenko D.A., Bazhukov A.A. Strength estimation of fractured rock using compression – a spe-cimen with spherical indenters. ISRM Regional Symposium-EUROCK 2018, 22-26 May 2018, St. Petersburg, Russia. OnePetro, 2018.
- N ISRM-EUROCK-2018-034.
- Rozanov A.O., Petrov D.N., Rozenbaum A.M., Tereshkin A.A. Acoustic Emission Precursor Criteria of Rock Damage. ISRM Regional Symposium-EUROCK 2018, 22-26 May 2018, St. Petersburg, Russia. OnePetro, 2018. N ISRM-EUROCK-2018-090.
- Il'inov M.D., Kartashov Yu.M. Accelerated method for determining the rheological properties of rocks. Journal of Mining Institute. 2011. Vol. 190, p. 207-209.
- Jin Yu, Xu Chen, Yan-yan Cai, Hong Li. Triaxial test research on mechanical properties and permeability of sandstone with a single joint filled with gypsum. KSCE Journal of Civil Engineering. 2016. Vol. 20. Iss. 6, p. 2243-2252. DOI: 10.1007/s12205-015-1663-7
- Liu C., Yu B., Zhang D., Zhao H. Experimental study on strain behavior and permeability evolution of sandstone under constant amplitude cyclic loading‐unloading. Energy Science & Engineering. 2020. Vol. 8. Iss. 2, p. 452-465. DOI: 10.1002/ese3.527
- Sakhaee-Pour A., Agrawal A. Predicting breakdown pressure and breakdown cycle in cyclic fracturing. SPE Production & Operations. 2018. Vol. 33. Iss. 4, p. 761-769. DOI: 10.2118/191137-PA
- Zhang D., Yang Y., Chu Y., Zhang X. Influence of loading and unloading velocity of confining pressure on strength and permeability characteristics of crystallines and stone. Results in Physics. 2018. Vol. 9, p. 1363-1370. DOI: 10.1016/j.rinp.2018.04.043
- Kallesten E., Andersen P., Berawala D. et al. Modeling of permeability and strain evolution in chemical creep compaction experiments with fractured and unfractured chalk cores conducted at reservoir conditions. SPE Journal. 2020. Vol. 25. Iss. 5, p. 2710-2728.
- DOI: 10.2118/197371-PA
- Nath F., Salvati P.E., Mokhtari M. et al. Laboratory Investigation of Dynamic Strain Development in Sandstone and Carbonate Rocks Under Diametrical Compression Using Digital-Image Correlation. SPE Journal. 2019. Vol. 24. Iss. 1, p. 254-273.
- DOI: 10.2118/187515-PA
- Rafieepour S., Miska S.Z., Ozbayoglu E.M. et al. Experimental Investigation of Depletion-and Injection-Induced Changes in Poromechanical, Transport, and Strength Properties of High-Porosity Sandstone. SPE Journal. 2021. Vol. 26. Iss. 5, p. 2793-2813. DOI: 10.2118/205364-PA
- Luo X., Were P., Jianfeng Liu J., Hou Z. Estimation of Biot’s effective stress coefficient from well logs. Environmental earth sciences. 2015. Vol. 73. Iss. 11, p. 7019-7028. DOI: 10.1007/s12665-015-4219-8
- Qiao L.P., Wong R.C.K., Aguilera R. Kantzas A. Determination of Biot's effective-stress coefficient for permeability of
- Nikanassin sandstone. Journal of Canadian Petroleum Technology. 2012. Vol. 51. Iss. 03. DOI: 10.2118/150820-PA
- Terzaghi K. The shearing resistance of saturated soils and the angle between the planes of shear. First international conference on soil Mechanics. 1936. Vol. 1, p. 54-59.
- Jun He, Zhenhua Rui, Kegang Ling. A new method to determine Biot's coefficients of Bakken samples. Journal of Natural Gas Science and Engineering. 2016. Vol. 35. Part A, p. 259-264. DOI: 10.1016/j.jngse.2016.08.061
- Li Q., Aguilera R., Cinco-Ley H. A Correlation for Estimating the Biot Coefficient. SPE Drilling & Completion. 2020. Vol. 35. Iss. 2, p. 151-163. DOI: 10.2118/195359-PA
- Aldana Gallego I.C., Santos L.P., Yucel Akkutlu I. A Laboratory Method for Estimation of Storage Capacity of Rock Samples under Effective Stress. SPE Journal. 2021. Vol. 26. Iss. 6, p. 3725-3741. DOI: 10.2118/195552-PA
- Civan F. Compressibility, porosity, and permeability of shales involving stress shock and loading/unloading hysteresis.
- SPE Journal. 2019. Vol. 24. Iss. 6, p. 2458-2481. DOI: 10.2118/195676-PA
- El Faidouzi M.M. Contribution of Tidal Analysis to Reservoir Monitoring: A Field Case Study in a Fractured Reservoir Offshore Abu Dhabi, UAE. SPE Reservoir Evaluation & Engineering. 2020. Vol. 23. Iss. 4, p. 1440-1457. DOI: 10.2118/188837-PA
- Civan F. Effective-Stress Coefficients of Porous Rocks Involving Shocks and Loading/Unloading Hysteresis. SPE Journal. 2021. Vol. 26. Iss. 01, p. 44-67. DOI: 10.2118/200501-PA
- David C., Wong T., Zhu W., Zhang J. Laboratory measurement of compaction-induced permeability change in porous rocks: Implications for the generation and maintenance of pore pressure excess in the crust. Pure and Applied Geophysics. 1994. Vol. 143. Iss. 1, p. 425-456. DOI: 10.1007/BF00874337
- Dong J., Hsu J., Wu W. et al. Stress-dependence of the permeability and porosity of sandstone and shale from TCDP Hole-A. International Journal of Rock Mechanics and Mining Sciences. 2010. Vol. 47. Iss. 7, p. 1141-1157. DOI: 10.1016/j.ijrmms.2010.06.019
