Обоснование аналитических зависимостей для гидравлического расчета транспорта высоковязких нефтей

А. К. Николаев; Н. А. Зарипова

doi:10.31897/PMI.2021.6.10

Том 252

Страницы:

885-895

Скачать том:

RUS ENG

Научная статья

Обоснование аналитических зависимостей для гидравлического расчета транспорта высоковязких нефтей

Авторы:

А. К. Николаев¹

Н. А. Зарипова²

Об авторах

1 — д-р техн. наук профессор Санкт-Петербургский горный университет ▪ Orcid
2 — аспирант Санкт-Петербургский горный университет ▪ Orcid

Дата отправки:

2021-02-28

Дата принятия:

2021-11-30

Дата публикации:

2021-12-27

Аннотация

Одно из приоритетных направлений развития нефтегазовой отрасли – поддержание в исправном состоянии газопроводных и нефтепроводных сетей, а также развитие подключенных к трубопроводам газовых и нефтяных месторождений арктической зоны РФ – перспективного региона, ресурсный потенциал которого позволит не только обеспечить значительную часть внутренних и внешних потребностей в различных видах сырья и первичных энергоносителях, но и принесет большой экономический эффект для недропользователей и государства. Одними из наиболее привлекательных регионов арктической зоны являются минерально-сырьевые центры Надым-Пурской и Пур-Тазовской нефтегазоносных областей. Необходимо разработать научно обоснованный подход к улучшению способов транспортировки нефти от промысла к существующим магистралям. Как известно, задача повышения эффективности трубопроводного транспорта высоковязкой нефти неразрывно связана с решением задач в области теплового и гидравлического расчета трубопроводной системы. В статье представлено обоснование зависимостей гидравлического расчета нефтепроводов, транспортирующих высоковязкие нефти, проявляющие сложные реологические свойства. На основе законов гидравлики неньютоновских жидкостей предложены формулы расчета потерь напора для жидкостей, подчиняющихся закону Оствальда, показана их связь с классическими уравнениями гидравлики. Рассмотрено теоретическое обоснование прокладки лупинга для увеличения эффективности трубопроводного транспорта высоковязкой нефти с учетом полученных зависимостей для степенной жидкости.

Область исследования:

Нефтегазовое дело

Ключевые слова:

высоковязкая нефть транспортировка нефти гидравлический расчет реологические свойства потери напора производительность нефтепровода степенная жидкость

10.31897/PMI.2021.6.10

Введение

Трудность обеспечения рационального режима транспортирования высоковязкой нефти в арктической зоне обусловлена сложными реологическим свойствами перекачиваемой нефти и суровыми климатическими условиями, которые являются исходными данными при выборе способа транспортирования и формирования технико-конструктивных решений по прокладке трубопровода [24]. В целях обеспечения стабильности работы нефтепровода необходимо на этапе проектирования выполнять гидравлический расчет. Гидравлический расчет неизотермических трубопроводов представляет собой наиболее важную для технологических расчетов задачу, решаемую в целях обеспечения стабильности работы нефтепроводной системы [3, 4]. Понижение гидравлического сопротивления возможно различными путями [11, 26, 32]. Наиболее широко применяемыми являются способы, направленные на изменение реологических свойств нефти. Например, в работах [10, 22, 23] рассмотрено улучшение реологических свойств посредством термообработки нефти. Работы [1, 6, 14] посвящены перекачке нефти с различными присадками. Также используются способы смешения нефтей, обладающих различными свойствами [8, 17, 25], гидротранспорт [5, 15, 28], физико-химическая обработка [17, 27, 31], либо комбинирование указанных методов [16, 18, 30]. Однако, это не снимает необходимость анализа теплогидравлических процессов.

В настоящее время формулы для аналитического расчета движения высоковязких нефтей в форме уравнения Лейбензона получены только для вязкопластичной жидкости [2]. Согласно анализу, представленному в [7] и методике РД 39-30-139-79, можно сделать вывод о том, что существующие формулы, используемые для гидравлического расчета движения неньютоновских жидкостей тяжеловесны и непригодны для аналитической оценки процессов трубопроводного транспорта высоковязких нефтей.

Методология

В статье выполнен анализ работ [1, 7, 9, 29, 34] в части исследования существующих зависимостей, применяемых для гидравлического расчета неизотермических трубопроводов, на основании которого сделаны выводы о несовершенстве существующих формул. В практике расчетов применяются формулы Дарси – Вейсбаха (преимущественно для компьютерных расчетов) и Лейбензона (для аналитических выкладок).

Классическая формула Дарси – Вейсбаха описывает потери напора на трение по длине трубопровода в зависимости от определяющих параметров [7]:

h_{τ} = λ \frac{L}{d} \frac{v^{2}}{2 g}, (1)

где λ – коэффициент гидравлического сопротивления; L – длина трубопровода; d – внутренний диаметр трубопровода; g – ускорение свободного падения; v – средняя скорость потока жидкости.

Основную сложность при расчете по формуле Дарси – Вейсбаха представляет определение коэффициента гидравлического сопротивления, для которого предложено большое количество расчетных формул [9].

Наилучшую сходимость с экспериментальными данными и серьезное теоретическое обоснование имеют формулы Кольбрука – Уайта, Черчилля и Хааланда [34]. Коэффициент гидравлического сопротивления по формуле Кольбрука – Уайта вычисляется следующим образом:

λ = {[2 lg (\frac{2,51}{Re \sqrt{λ}} + \frac{Δ}{3,7 d})]}^{- 2}, (2)

где Re – число Рейнольдса; Δ – шероховатость внутренней поверхности трубы.

Формула Черчилля, применимая во всем диапазоне чисел Рейнольдса, с учетом коэффициентов представлена в следующем виде [7, 29]:

λ = 8 {[{(\frac{8}{Re})}^{12} + {(A + B)}^{- 1,5}]}^{1 / 12}, (3)

A = {[- 2,457 \ln ({(\frac{7}{Re})}^{0,9} + 0,27 (Δ / d))]}^{16}, (4)

B = {(\frac{37530}{Re})}^{16} . (5)

В зарубежной литературе рекомендуют использовать формулу Хааланда, которая справедлива в диапазоне 4·10³ < Re < 10⁸[7, 29],

\frac{1}{\sqrt{λ}} = - 1,8 \log_{10} ({(\frac{\frac{Δ}{d}}{3,7})}^{1,11} + (\frac{6,9}{Re})) . (6)

Для расчета коэффициента гидравлического сопротивления неньютоновской жидкости, подчиняющейся степенному закону, в работе [1] предложена формула

\frac{1}{\sqrt{λ}} = \frac{0,88}{n} \ln [k (n) Re {(\frac{λ}{8})}^{1 - n / 2}] - 2,83, (7)

k (n) = 2^{1 - n / 2} exp [n (2,83 - \frac{0,2}{n^{1,2}}) / 0,88], (8)

где n – показатель степени.

Формула (7) справедлива в области турбулентного течения степенной жидкости. Для различных диапазонов значений показателя степени n предложены упрощенные аппроксимационные зависимости [7]:

п р и 0,2 \leq n \leq 0,5 λ {Re}^{1 / 3} = 0,698 n - 1,94 \cdot 10^{- 2}; (9)

п р и 0,5 < n \leq 1,25 λ {Re}^{1 / 4} = 0,353 n - 3,80 \cdot 10^{- 2}; (10)

п р и 1,25 < n \leq 2,0 λ {Re}^{1 / 5} = 0,234 n - 5,13 \cdot 10^{- 2} . (11)

В случае транспортирования высоковязких нефтей возможно применение депрессорных присадок и иных методов обработки [19-21], однако они в полной мере не решают возникающие осложнения.

Формула Лейбензона, полученная в предположении λ=А / Re^m, в общем виде записывается как

h_{τ} = β \frac{Q^{2 - m} ν^{m}}{d^{5 - m}} L, (12)

где A, b и m – числовые коэффициенты, зависящие от режима движения жидкости; ν – коэффициент кинематической вязкости нефти; Q – объемный расход перекачиваемого продукта.

Очевидное преимущество формулы Лейбензона – аналитический характер, который позволяет наглядно связать основные параметры трубопроводного транспорта – расход, вязкость, диаметр и длину трубопровода с потерями напора. В дальнейшем это можно использовать для анализа методов увеличения пропускной способности и т.п.

В работе [35] (табл.1) доказана универсальность формулы Лейбензона для широкой номенклатуры перекачиваемых продуктов и режимов течения.

Несмотря на большую проделанную работу, в настоящее время формулы для аналитического расчета движения высоковязких нефтей в форме уравнения Лейбензона получены только для вязкопластичной жидкости.

Обсуждение

Формула Лейбензона для вязкопластичной жидкости:

h_{τ} = β \frac{Q^{2 - m} ν^{m} {(1 + \frac{τ_{0} π d^{3}}{6 μ Q})}^{m}}{d^{5 - m}} L, (13)

где μ – коэффициент динамической вязкости жидкости; τ₀ –начальное напряжение сдвига; гидравлический уклон можно представить в виде выражения

i = β \frac{Q^{2 - m} ν^{m} {(1 + \frac{τ_{0} π d^{3}}{6 μ Q})}^{m}}{d^{5 - m}} . (14)

Коэффициенты формулы Лейбензона при различных режимах течения:

\begin{matrix} β = 4,15 с^{2} /м, m = 1, Re \leq 2,3 \cdot 10^{3} (1 + \frac{И}{6}); \\ β = 0,0247 с^{2} /м, m = 0,25, 10^{4} (1 + \frac{И}{6}) \leq Re \leq 10^{5}; \\ β = 0,089 {(\frac{Δ}{d})}^{0,25} с^{2} /м, m = 0, Re > 500 \frac{d}{Δ}, \end{matrix} (15)

где И – число Ильюшина, И = t₀/mν, характеризует отношение начального напряжения сдвига к напряжению вязкого трения; ∆ – абсолютная шероховатость стенок труб.

Таблица 1

Коэффиценты в обобщенной формуле Лейбензона для расчетов при перекачке нефти и нефтепродуктов, природного газа и сжижженных газов

Примечания.
1. $\overline{k}$ - величина относительной шереховатости трубопровода.
2. В ламинарном режиме - кроме трубопроводов, по которым перекачиваются жидкости с противотурбулентными присадками [12].
3. В турбулентном режиме - при перекчке нефти, нефтепродуктов и сжижженных газов без противотурбулентных присадок ƒ(θ)=1 [6].

При ламинарном режиме для расчета коэффициента гидравлического сопротивления степенной жидкости используется формула Мецнера – Рида [33]:

λ = \frac{64}{{Re}_{M R}}, (16)

где – обобщенное число Рейнольдса, определяемое по формуле

{Re}_{M R} = \frac{ρ u^{(2 - n)} d^{n}}{8^{(n - 1)} k {(\frac{3 n + 1}{4 n})}^{n}}, (17)

u – скорость течения нефти; k – показатель консистенции степенной жидкости.

Для определения коэффициента гидравлического сопротивления при турбулентном течении степенной жидкости Ирвин предложил использовать следующую зависимость [2, 7]:

λ = 4 {(\frac{D (n)}{{Re}_{M R}})}^{(\frac{1}{3 n + 1})}, (18)

D (n) = \frac{2^{(n + 4)}}{7^{7 n}} {(\frac{4 n}{3 n + 1})}^{3 n^{2}} . (19)

Критическое число Рейнольдса предлагается определять в соответствии с зависимостью Райна – Джонсона

{Re}_{M R} = \frac{6464 n}{{(3 n + 1)}^{2}} {(2 + n)}^{(\frac{2 + n}{1 + n})} . (20)

Формулу (17) можно переписать в соответствии с зависимостью, используемой Лейбензоном при выводе своей формулы,

λ = \frac{A}{{Re}_{M R}^{m^{*}}} . (21)

Тогда показатель степени числа Рейнольдса определится как

m^{*} = \frac{1}{3 n + 1} . (22)

В формуле (21) коэффициент А вычисляется, исходя из зависимости

A = 4 D {(n)}^{(\frac{1}{3 n + 1})} . (23)

График зависимости коэффициента A от показателя степени n в степенном законе течения жидкости представлен на рис.1.

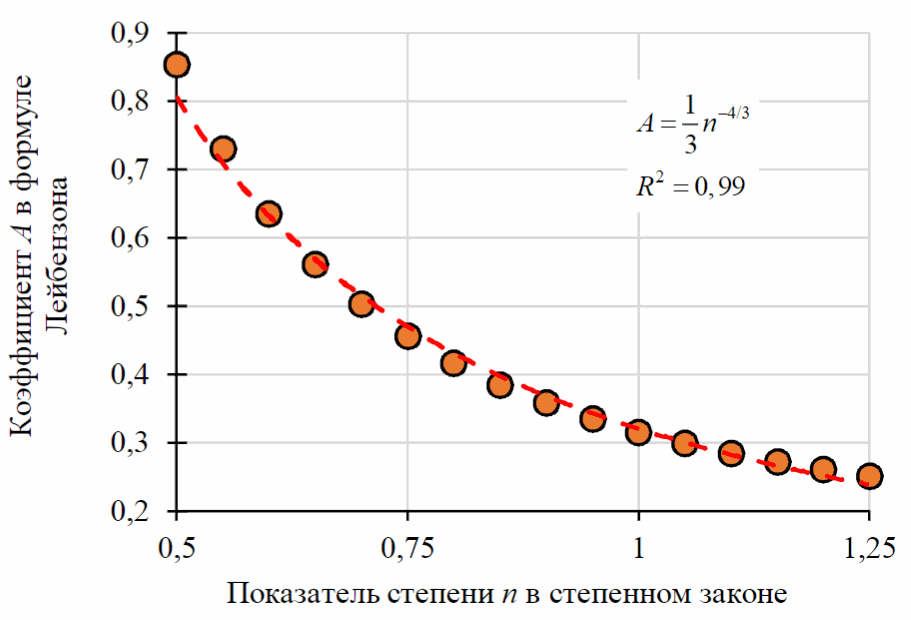
Рис.1. График зависимости коэффициента от показателя степени n в степенном законе течения жидкости

В результате регрессионной обработки полученных данных установлено, что коэффициент A с достаточной точностью описывается зависимостью вида:

\begin{array}{l} A = \frac{n^{- \frac{4}{3}}}{3} \\ R^{2} = 0,99 \end{array}

Начнем вывод модифицированной формулы Лейбензона для степенной жидкости с рассмотрения классической формулы Дарси – Вейсбаха

h_{l} = λ \frac{l}{d} \frac{v^{2}}{2 g} (25)

и с учетом того, что расход нефти $ Q=\frac{\pi d^2}{4} \nu $, получим выражение для потерь на трение в нефтепроводе

h_{l} = \frac{A l \cdot 16 Q^{2}}{{Re}_{M R}^{m} d 2 g π^{2} d^{4}} . (26)

Представим обобщенное число Рейнольдса в удобной для дальнейших преобразований форме:

{Re}_{M R}^{m} = {(\frac{ρ v^{2 - n} d^{n}}{8^{n - 1} k {(\frac{3 n + 1}{4 n})}^{n}})}^{\frac{1}{3 n + 1}} = {(\frac{ρ {(\frac{4 Q}{π d^{2}})}^{2 - n} d^{n}}{8^{n - 1} k {(\frac{3 n + 1}{4 n})}^{n}})}^{\frac{1}{3 n + 1}} = {(\frac{4^{2 - n}}{π^{2 - n} 8^{n - 1} {(\frac{3 n + 1}{4 n})}^{n}})}^{\frac{1}{3 n + 1}} \frac{Q^{\frac{2 - n}{3 n + 1}} d^{\frac{3 n - 4}{3 n + 1}}}{{(\frac{k}{ρ})}^{\frac{1}{3 n + 1}}} . (27)

Тогда с учетом выражения (26), после ряда преобразований выражение для потерь напора на трение запишется в виде:

h_{l} = \frac{16 n^{- \frac{4}{3}}}{2 g π^{2} \cdot 3 {(\frac{4^{2 - n}}{8^{n - 1} k {(\frac{3 n + 1}{4 n})}^{n} π^{2 - n}})}^{\frac{1}{3 n + 1}}} \frac{l Q^{2 - \frac{2 - n}{3 n + 1}} {(\frac{k}{ρ})}^{\frac{1}{3 n + 1}}}{d^{5 + \frac{3 n - 4}{3 n + 1}}} = β \frac{l {(\frac{k}{ρ})}^{m} Q^{\frac{7 n}{3 n + 1}}}{d^{6 - 5 m}} . (28)

В выражении (28) следует упростить коэффициент b, который определяется по формуле

β = \frac{16 n^{- \frac{4}{3}}}{2 g π^{2} \cdot 3 {(\frac{4^{2 - n}}{8^{n - 1} k {(\frac{3 n + 1}{4 n})}^{n} π^{2 - n}})}^{\frac{1}{3 n + 1}}} . (29)

График зависимости коэффициента b от показателя степени n в формуле Лейбензона представлен на рис.2, а.

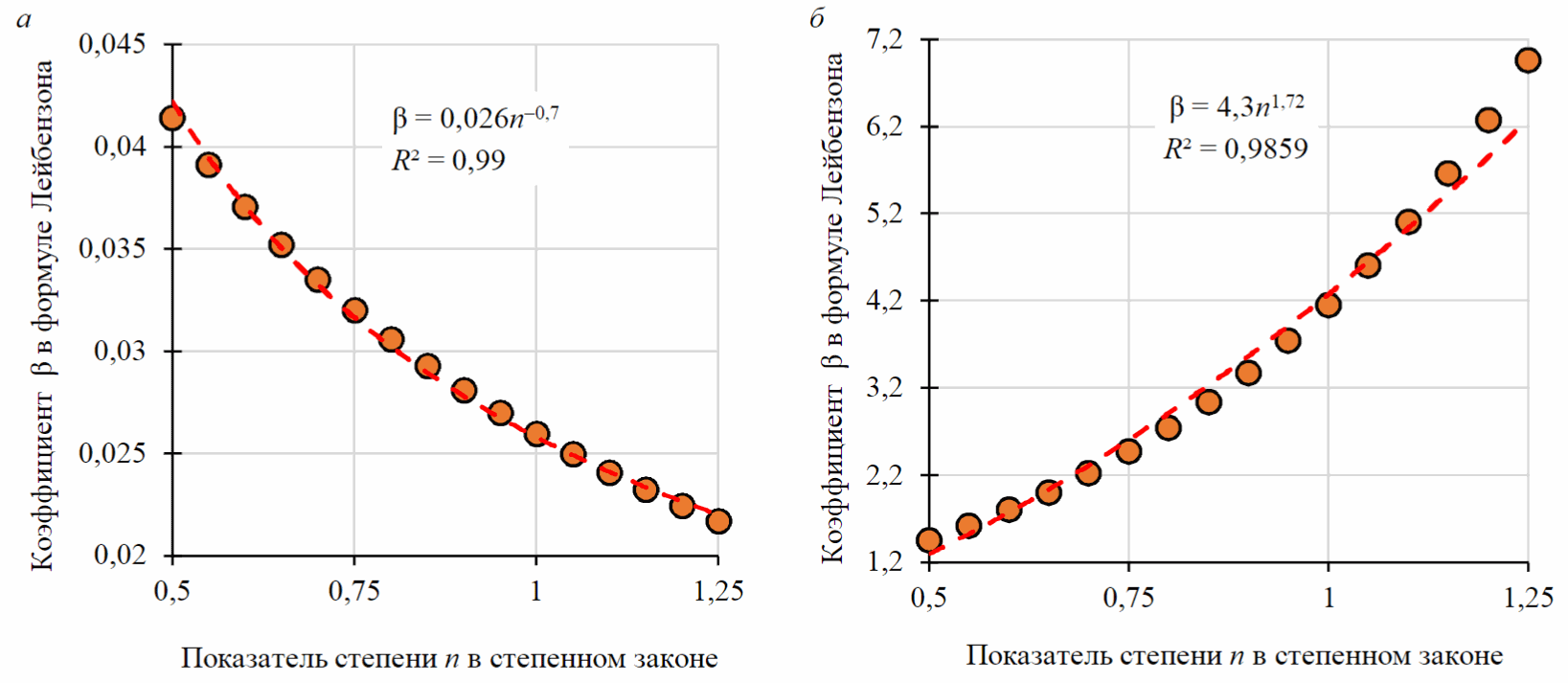
Рис.2 График зависимости коэффициента β от показателя степени n в формуле Лейбензона а - турбулентный режим; б - ламинарный режим

Повторив те же действия по обработке данных, что и с коэффициентом A, установлено, что коэффициент β с достаточной точностью описывается зависимостью вида:

β = 0,026 n^{- 0,7} . (30)

Окончательно получаем модифицированное уравнение Лейбензона для потерь напора степенной жидкости при турбулентном движении в трубопроводе, верное для диапазона показателей степени 0,5 ≤ n≤ 1,25,

h = β \frac{l {(\frac{k}{ρ})}^{m} Q^{\frac{7}{3} (1 - m)}}{d^{6 - 5 m}} . (31)

Cледуя той же логике рассуждений, повторим действия для ламинарного режима течения степенной жидкости. Для этого случая график зависимости коэффициента β от показателя степени n в формуле Лейбензона представлен на рис.2, б.

Коэффициенты A= 64 и m = 1 для ламинарного режима течения степенной жидкости, очевидно, следуют из зависимости (21).

Обобщение полученных коэффициентов показано в табл.2.

Таблица 2

Обобщение полученных результатов по модифицированной формуле Лейбензона для степенной жидкости

Режим течения

Диапазон

применимости

Зависимость для измеренияпотерь напора по длине

A

β, с²/м

m^*

Турбулентный

0,5 ≤ n ≤ 1,25

(относительная

погрешность результатовв указанном диапазонене превышает 2 %)

h = β \frac{l {(\frac{k}{ρ})}^{m^{*}} Q^{\frac{7}{3} (1 - m^{*})}}{d^{6 - 5 m^{*}}}

\frac{n^{- \frac{4}{3}}}{3}

0,026 n^{- 0,7}

\frac{1}{3 n + 1}

Ламинарный

h = β \frac{l (\frac{k}{ρ}) Q^{n}}{d^{3 n + 1}}

64

4,3 n^{1,7}

1

Из табл.2 можно сделать следующий вывод: коэффициент β при ламинарном режиме течения при n → 1 близок к таковому в формуле Стокса для ньютоновской жидкости (β = 4,15), а при турбулентном течении – к формуле Блазиуса (β = 0,0246). Искусственная подгонка коэффициента для придания формулам смысловой законченности очевидно возможна, но влечет увеличение их погрешности на 5 %.

Повышение гидравлической эффективности – одна из основных задач в области трубопроводного транспорта нефти [2, 13, 14]. Работа трубопровода, как правило, сопровождается изменениями в режиме перекачки. Если повышение параметров перекачки (расход, температура нефти) находится в пределах проектных величин, то работа трубопровода не вызывает опасений, но если это повышение выше проектных величин, то необходимо проверить «горячий» трубопровод на прочность и устойчивость (линейную часть и обвязку станций), а также уточнить условия работы насосов на всасывание, утечки, температурный режим. В первые годы разработки нефтяного месторождения количество добываемой нефти меньше, чем при полной его загрузке. При развитии месторождения объемы перекачиваемой нефти могут быть увеличены, в связи с этим необходимо предусмотреть дополнительные технические решения, позволяющие повысить эффективность транспортировки добываемой нефти.

Рассмотрим теоретическое обоснование прокладки лупинга как эффективного способа повышения эффективности транспортирования высоковязкой нефти. Гидравлический уклон трубопровода, перекачивающего степенную жидкость,

i_{тр} = β \frac{{(\frac{k}{ρ})}^{m^{*}} Q^{\frac{7}{3} (1 - m^{*})}}{d_{тр}^{6 - 5 m^{*}}} . (32)

Расход жидкости в трубопроводе определяется как

Q_{тр} = \sqrt[\frac{7}{3} (1 - m^{*})]{i_{тр} \frac{d_{тр}^{6 - 5 m^{*}}}{{(\frac{k}{ρ})}^{m^{*}} β}} . (33)

Таким же образом можно найти расход в лупинге:

Q_{л} = \sqrt[\frac{7}{3} (1 - m^{*})]{i_{л} \frac{d_{л}^{6 - 5 m^{*}}}{{(\frac{k}{ρ})}^{m^{*}} β}} . (34)

Суммарный расход в нефтепроводе есть сумма расходов в основном трубопроводе и лупинге:

Q = Q_{л} + Q_{тр} = Q = \sqrt[\frac{7}{3} (1 - m^{*})]{\frac{i_{л}}{{(\frac{k}{ρ})}^{m^{*}} β}} (d_{тр}^{\frac{6 - 5 m^{*}}{\frac{7}{3} (1 - m^{*})}} + d_{л}^{\frac{6 - 5 m^{*}}{\frac{7}{3} (1 - m^{*})}}) . (35)

Преобразуем выражение (33):

Q^{\frac{7}{3} (1 - m^{*})} = \frac{i_{л}}{{(\frac{k}{ρ})}^{m^{*}} β} {(d_{тр}^{\frac{6 - 5 m^{*}}{\frac{7}{3} (1 - m^{*})}} (1 + {(\frac{d_{л}}{d_{тр}})}^{\frac{6 - 5 m^{*}}{\frac{7}{3} (1 - m^{*})}}))}^{\frac{7}{3} (1 - m^{*})} . (36)

Гидравлический уклон для лупинга выражается как

i_{л} = β \frac{{(\frac{k}{ρ})}^{m^{*}} Q^{\frac{7}{3} (1 - m^{*})}}{d^{6 - 5 m^{*}}} {(\frac{1}{1 + {(\frac{d_{л}}{d_{тр}})}^{\frac{6 - 5 m^{*}}{\frac{7}{3} (1 - m^{*})}}})}^{\frac{7}{3} (1 - m^{*})} = i ω . (37)

Окончательно получаем коэффициент, учитывающий наличие лупинга,

ω_{т}^{*} = \frac{1}{{(1 + {(\frac{D_{л}}{D_{тр}})}^{\frac{6 - 5 m^{*}}{\frac{7}{3} (1 - m^{*})}})}^{\frac{7}{3} (1 - m^{*})}} . (38)

Для маловязких нефтей это соотношение записывается в виде

ω = \frac{1}{{(1 + {(\frac{D_{л}}{D_{тр}})}^{\frac{5 - m}{2 - m}})}^{2 - m}} . (39)

Коэффициент увеличения пропускной способности

χ_{л} = \frac{1}{{[1 - \frac{l_{л}}{L_{тр}} (1 - ω)]}^{\frac{1}{2 - m}}} . (40)

Сравнивая величины коэффициентов, учитывающих наличие лупинга, получаем график ряда зависимостей (рис.3).

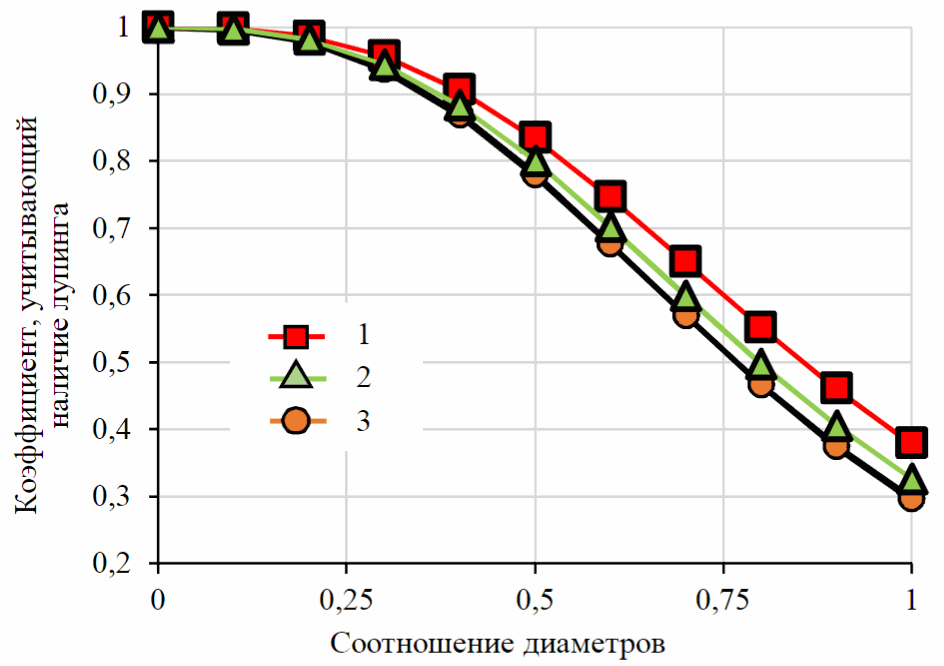
Рис.3. График зависимости коэффициента, учитывающего наличие лупинга, от соотношения диаметров для различных типов нефтей 1 – ньютоновская жидкость (n = 1); 2 – степенная жидкость (n = 0,5); 3 – степенная жидкость (n = 0,75)

Из рис.3 можно сделать несколько выводов:

максимальное отличие достигается при соотношении диаметров, равном единице, и при наиболее выраженном отклонении от ньютоновского характера течения жидкости;
в силу незначительного отличия коэффициента, учитывающего наличие лупинга (при n=0,75 и D_л/D_тр = 1 составляет не более 10 %), можно полагать, что при соблюдении иных технических решений в части обеспечения теплового режима коэффициент увеличения пропускной способности будет близок к коэффициенту для маловязких нефтей.

Представленные расчеты по обоснованию лупинга выполнены на основании полученной модифицированной формулы Лейбензона и учитывают свойства степенной жидкости. Из графика на рис.3 видно, что отличие коэффициента, учитывающего наличие лупинга для ньютоновской и степенной жидкости незначительно (менее 10 %), что позволяет сделать выводы об эффективности применения лупинга как средства увеличения пропускной способности при развитии месторождения.

Заключение

Выполнен расчет и обоснование модифицированной формулы Лейбензона для вязкопластичной жидкости, что позволит разработать математическую модель функционирования нефтепровода циклического действия, транспортирующего высоковязкую нефть.

Установлено, что гидравлический расчет нефтепроводов, транспортирующих нефть, реологические свойства которой описываются степенным законом, допустимо проводить по модифицированной формуле Лейбензона в диапазоне 0,5 ≤ n ≤ 1,25. Относительная погрешность полученного соотношения не превосходит 2 %. Важно отметить, что коэффициенты в полученных формулах в предельном случае n = 1 близки к таковым у ньютоновских нефтей, что свидетельствует о внутреннем единстве полученных зависимостей.

С учетом полученных зависимостей представлено теоретическое обоснование повышения производительности нефтепроводов, транспортирующих высоковязкие нефти путем прокладки лупинга.

Литература

Mitusova T.N., Kondrasheva N.K., Lobashova M.M. et al. Influence of Dispersing Additives and Blend Composition on Stability of Marine High-Viscosity Fuels. Journal of Mining Institute. 2017. Vol. 228, p. 722-725. DOI: 10.25515/PMI.2017.6.722
Nikolaev A.K., Pshenin V.V., Zakirov A.I., Zaripova N.A. Choice of Optimal Parameters of Bituminous Oil Transportation on the Example Ashalchinsky Field. Equipment and Technologies for Oil and Gas Complex. 2017. N 1, p. 53-59 (in Russian).
Didkovskaya A.S., Lurie M.V. Iterative Algorithm of Hydraulic Calculation of the Non-Isothermal Oil Transfer. Science аnd Technologies: Oil and Oil Products Pipeline Transportation. 2016. N 2 (22), p. 50-55 (in Russian).
Didkovskaya A.S., Lurie M.V. A Universal Algorithm for Numerical Calculations of Stationary Modes of the Pipelines. Science аnd Technologies: Oil and Oil Products Pipeline Transportation. 2015. N 4 (20), p. 85-91 (in Russian).
Dolgii I.E. Methods to Enhance Oil Recovery in the Process of Complex Field Development of the Yarega Oil and Titanium Deposit. Journal of Mining Institute. 2018. Vol. 231, p. 263-267. DOI: 10.25515/PMI.2018.3.263
Zholobov V.V., Sinelnikov S.V., Ignatenkova A.I. The Prospects of Dra for Reducing the Energy Consumption of Thermal Stations in a “Hot” Pumping. Science аnd Technologies: Oil and Oil Products Pipeline Transportation. 2019. Vol. 9. N 3, p. 256-265. DOI: 10.28999/2541-9595-2019-9-3-256-265 (in Russian).
Zakirov A.I. Justification of modes for pipeline transport of bituminous oil: Avtoref. dis. … kand. tekhn. nauk. St. Petersburg: Sankt-Peterburgskiy gornyy universitet, 2016, p. 20 (in Russian).
Aralov O.V., Buyanov I.V., Savanin A.S., Iordansky E.I. Research of Methods for Oil Kinematic Viscosity Calculation in the Oil-Trunk Pipeline. Science аnd Technologies: Oil and Oil Products Pipeline Transportation. 2017. Vol. 7. N 5, p. 97-105 (in Russian).
Kislitsyn M.S., Yaroshenko V.V. Prospects of oil mining at Yarega field. Mining Informational and Analytical Bulletin. 2018. N 1, p. 12-18. DOI: 10.25018/0236-1493-2018-1-0-12-18 (in Russian).
Kondrasheva N.K., Baitalov F.D., Boitsova A.A. Comparative Assessment of Structural-Mechanical Properties of Heavy Oils of Timano-Pechorskaya Province. Journal of Mining Institute. 2017. Vol. 225, p. 320-329. DOI: 10.18454/PMI.2017.3.320
Lurie M.V. Computation Algorithm of Quasi-Steady-State Modes of Nonisothermal Oil Pumping. Oil and Oil Products Pipeline Transportation. 2014. N 2 (14), p. 28-31 (in Russian).
Katsal I.N., Lyapin A.Yu., Dubovoy E.S. et al. On the Formation of Oil Traffic in Oil Trunk Pipelines System of JSC Transneft. Science аnd Technologies: Oil and Oil Products Pipeline Transportation. 2016. N 2 (22), p. 92-95 (in Russian).
Revel-Muroz P.A., Fridlyand Ya.M., Kutukov S.E., Golyanov A.I. Assessing the Hydraulic Efficiency of Oil Pipelines According to the Monitoring of Process Operation Conditions. Science аnd Technologies: Oil and Oil Products Pipeline Transportation. 2019. Vol. 9. N 1, p. 8-19. DOI: 10.28999/2541-9595-2019-9-1-8-19
Revel-Muroz P.A., Fridland Ya.M., Kutukov S.E. et al. Estimation of the Oil Pumping Technology Effectiveness with Drag Reduction Agents. Oil Industry. 2020. N 1, p. 90-95. DOI: 10.24887/0028-2448-2020-1-90-95 (in Russian).
Rushd S., Rahman A. A Study on Friction Loss and Holdup Ratio in the Water Lubricated Pipeline Transportation of Heavy Oil. Science аnd Technologies: Oil and Oil Products Pipeline Transportation. 2019. Vol. 9. N 2, p. 200-206. DOI: 10.28999/2541-9595-2019-9-2-200-206 (in Russian).
Semin S.L., Fedorov P.V. Optimization of Main Pipeline Process Parameters with Operating Oil Heating Stations and Anti-Turbulent Additives. Science аnd Technologies: Oil and Oil Products Pipeline Transportation. 2018. Vol. 8. N 6, p. 650-655 (in Russian).
Sunagatullin R.Z., Karimov R.M., Dmitriev M.E., Baykova M.I. Experimental Studies of the Operational Properties of Asphaltene-Resin-Paraffin Deposits Formed in Main Oil Pipelines. Science аnd Technologies: Oil and Oil Products Pipeline Transportation. 2018. Vol. 8. N 4, p. 398-406. DOI: 10.28999/2541-9595-2018-8-4-398-406
Surikov V.I., Shiryaev A.M., Lukmanov M.R. et al. About the Research of the Thermal and Ultrasonic Fields Influence on the Rheological Characteristics of High-Viscosity Oils. Science аnd Technologies: Oil and Oil Products Pipeline Transportation. 2015. N 2 (18), p. 21-25 (in Russian).
Fedorov V.T., Kazakov V.V., Tchelinzew S.N. Technological Development in Application of a Depressor Additive in the Condition if High Viscous Oil Blend Transportation in Timano-Pechorskaya Oil-And-Gas-Bearing Province. Science аnd Technologies: Oil and Oil Products Pipeline Transportation. 2013. N 2 (10), p. 28-32 (in Russian).
Fedorov P.V., Lukmanov M.R. Impact of Rheological Properties of Oil On Pipeline Operation Energy Efficiency. Science аnd Technologies: Oil and Oil Products Pipeline Transportation. 2020. Vol. 10. N 1, p. 8-16. DOI: 10.28999/2541-9595-2020-10-1-8-16 (in Russian).
Fedorov P.V., Nekuchaev V.O., Pyustin A.A. Study of the Heat Treatment Influence on the Rheological Characteristics of High-Viscosity Oils. Science аnd Technologies: Oil and Oil Products Pipeline Transportation. 2016. N 6 (26), p. 58-63 (in Russian).
Huayi Jiang, Bo Сао. Composition аnd Property Change of Heavy High-Viscosity Oil under the Influence of Microwave Radiation. Science аnd Technologies: Oil and Oil Products Pipeline Transportation. 2013. N 4 (12), p. 20-25 (in Russian).
Huayi Jiang, Bo Сао. Evaluation of Temperature Distribution in Microphysical Model of Heavy Oil under the Influence of Microwave Radiation. Science аnd Technologies: Oil and Oil Products Pipeline Transportation. 2014. N 1 (13), p. 48-52 (in Russian).
Cherepovitsyn А.Е., Lipina S.А., Evseeva О.О. Innovative Approach to the Development of Mineral Raw Materials of the Arctic Zone of the Russian Federation. Journal of Mining Institute. 2018. Vol. 232, p. 438-444. DOI: 10.31897/PMI.2018.4.438
Sunagatullin R.Z., Karimov R.M., Tashbulatov R.R., Mastobaev B.N. Modeling the Thermal-Hydraulic Effect of Wax Layer. Science аnd Technologies: Oil and Oil Products Pipeline Transportation. 2019. Vol. 9. N 2, p. 158-162. DOI: 10.28999/2541-9595-2019-9-2-158-162 (in Russian).
Abarasi Hart. A review of technologies for transporting heavy crude oil and bitumen via pipelines. Journal of Petroleum Exploration and Production Technology. 2014. Vol. 4. Iss. 3, p. 327-336. DOI: 10.1007/s13202-013-0086-6
Alexandrov V.I., Vasilyeva M.A. Express-diagnosis of the technical state slurry pumps in systems hydrotransport processing tails of ore. Innovation-Based Development of the Mineral Resources Sector: Challenges and Prospects – 11th conference of the Russian-German Raw Materials, 7-8 November 2018, Potsdam, Germany. CRC Press, 2018, p. 273-282.
Aleksandrova T.N., Romashev A.O., Aleksandrov A.V. About modeling of rheological properties of heavy oil suspensions. Oil Industry. 2016. Vol. 2016. Iss. 5, p. 68-70.
Dejan Brkić. Review of explicit approximations to the Colebrook relation for flow friction. Journal of Petroleum Science and Engineering. 2011. Vol. 77. Iss. 1, p. 34-48. DOI: 10.1016/j.petrol.2011.02.006
Nikitin M., Saychenko L. The rheological properties of abnormally viscous oil. Petroleum Science and Technology. 2017. Vol. 36. Iss. 2, p. 136-140. DOI: 10.1080/10916466.2017.1410558
Palaev A.G., Shammazov I.A., Dzhemilev E.R. Research of the impact of ultrasonic and thermal effects on oil to reduce its viscosity. Journal of Physics. 2020. Vol. 1679 (5). DOI: 10.1088/1742-6596/1679/5/052073
Saniere A., Henaut I., Argillier J.F. Pipeline transportation of heavy oils, a strategic, economic and technological challenge. Oil & Gas Science and Technology. 2004. Vol. 59. Iss. 5, p. 455-466. DOI: 10.2516/ogst:2004031
Shangaraeva L., Klimko V. The application of the thermal stimulation in heavy oil recovery. Petroleum Science and Technology. 2016. Vol. 34. Iss. 23, p. 1894-1898. DOI: 10.1080/10916466.2016.1238934
Smirnova N.N., Izotov E.A. Methodology for estimating heat losses due to heat effects on a heterogeneous oil reservoir. Journal of Industrial Pollution Control. 2018. Vol. 33. Iss. 1, p. 950-958.
Valiev M.I., Korshak A.A. The use of the generalized formula of L.S.Leibenzon in the hydraulic calculation of pumping oil and petroleum products with small additives of polymers. Oil Industry. 2020. Vol. 2020. Iss. 8, p. 110-112. DOI: 10.24887/0028-2448-2020-8-110-112

Обоснование аналитических зависимостей для гидравлического расчета транспорта высоковязких нефтей

Аннотация

Введение

Методология

Обсуждение

Коэффиценты в обобщенной формуле Лейбензона для расчетов при перекачке нефти и нефтепродуктов, природного газа и сжижженных газов

Обобщение полученных результатов по модифицированной формуле Лейбензона для степенной жидкости

Заключение

Литература

Похожие статьи