Submit an Article
Become a reviewer
Vol 252
Pages:
885-895
Download volume:
RUS ENG
Research article
Oil and gas

Substantiation of analytical dependences for hydraulic calculation of high-viscosity oil transportation

Authors:
Alexander K. Nikolaev1
Natalia А. Zaripova2
About authors
  • 1 — Ph.D., Dr.Sci. Professor Saint Petersburg Mining University ▪ Orcid
  • 2 — Postgraduate Student Saint Petersburg Mining University ▪ Orcid
Date submitted:
2021-02-28
Date accepted:
2021-11-30
Date published:
2021-12-17

Abstract

One of the development priorities in oil and gas industry is to maintain gas and oil pipeline networks and develop pipeline-connected gas and oil fields of the Arctic zone of the Russian Federation, a promising region the resource potential of which will not only meet a significant portion of internal and external demand for various types of raw materials and primary energy carriers, but will also bring great economic benefits to subsoil users and the state. The mineral and raw material centers of the Nadym-Purskiy and Pur-Tazovskskiy oil and gas bearing areas are among the most attractive regions of the Arctic zone. It is necessary to develop a scientifically substantiated approach to improve the methods of oil transportation from the field to the existing pipelines. As it is known, the task of increasing the efficiency of pipeline transportation of high-viscosity oil is inseparably connected with solving problems in the field of thermal and hydraulic calculation of pipeline system. The article presents the substantiation of dependencies for hydraulic calculation of pipelines transporting high-viscosity oil exhibiting complex rheological properties. Based on the laws of hydraulics for non-Newtonian fluids, the formulas for calculating head losses for fluids obeying Ostwald's law are proposed, their relationship to the classical equations of hydraulics is shown. The theoretical substantiation of looping installation for increasing the efficiency of pipeline transportation of high-viscosity oil taking into account the received dependences for power fluid is considered.

Keywords:
high-viscosity oil transportation of oil hydraulic calculation rheological properties head losses pipeline performance power fluid
10.31897/PMI.2021.6.10
Go to volume 252

Introduction

The difficulty of ensuring the rational transportation mode of high-viscosity oil in the Arctic zone is caused by the complex rheological properties of the pumped oil and harsh climatic conditions, which are the initial data when choosing the method of transportation and forming technical and structural solutions for pipeline laying [24]. In order to ensure stability of oil pipeline operation it is necessary to perform hydraulic calculation at the design stage. Hydraulic calculation of non-isothermal pipelines is the most important task for technological calculations, solved in order to ensure stability of oil pipeline system operation [3, 4]. Reduction of hydraulic resistance is possible in various ways [11, 26, 32]. The most widely used methods are those aimed at changing the rheological properties of oil. For example, the works [10, 22, 23] consider the improvement of rheological properties through thermal treatment of oil. Works [1, 6, 14] are devoted to pumping oil with various additives. There are also methods of mixing crude oils with different properties [8, 17, 25], hydrotransportation [5, 15, 28], physical and chemical treatment [17, 27, 31], or a combination of these methods [16, 18, 30]. However, this does not negate the need to analyze the thermal and hydraulic processes.

At present, formulas for analytical calculation of high-viscosity oil motion in the form of Leibenzon equation have been obtained only for viscoplastic fluid [2]. According to the analysis presented in [7] and methodology RD 39-30-139-79, it can be concluded that the existing formulas used for hydraulic calculation of non-Newtonian liquids motion are heavy and unsuitable for analytical assessment of processes in pipeline transport of high-viscosity oil.

Methodology

The paper analyzes the works [1, 7, 9, 29, 34] with regard to the study of existing dependences used for hydraulic calculation of non-isothermal pipelines, based on which conclusions about imperfection of existing formulas are made. Darcy – Weissbach formulas (mainly for computer calculations) and Leibenzon formulas (for analytical calculations) are used in the practice of calculations.

The conventional Darcy – Weissbach formula describes the friction losses along the length of the pipeline, depending on the defining parameters [7]:

h τ =λ L d v 2 2g ,           (1)

where λ – hydraulic resistance coefficient; L – length of pipeline; d – pipeline inner diameter; g – acceleration of gravity; v – average velocity of fluid flow.

The main difficulty in calculating with Darcy – Weissbach formula is to determine the hydraulic resistance coefficient, for which a large number of calculation formulas are proposed [9].

The Colebrook-White, Churchill and Haaland formulas have the best agreement with experimental data and serious theoretical justification [34]. The hydraulic resistance coefficient by the Colebrook-White formula is calculated as follows:

λ= 2lg 2.51 Re λ + Δ 3.7d −2 ,           (2)

where Re – Reynolds number; Δ – roughness of the pipe inner surface.

Churchill formula, applicable over the entire range of Reynolds numbers, taking into account the coefficients, is as follows [7, 29]:

λ=8 8 Re 12 + A+B −1,5 1/12  ,           (3)
A= −2.457ln 7 Re 0.9 +0.27 Δ/d 16  ,           (4)
B= 37530 Re 16  .           (5)

The foreign literature recommends using the Haaland formula, which is valid in the range
4·103 < Re < 108 [7, 29],

1 λ =−1.8 log 10 Δ d 3.7 1.11 + 6.9 Re  .            (6)

To calculate the hydraulic resistance coefficient of a non-Newtonian fluid that obeys the power law, work [1] proposes the formula

1 λ = 0.88 n ln k n Re λ 8 1−n/2 −2.83 ,           (7)
k n = 2 1−n/2 exp n 2.83− 0.2 n 1.2 /0.88 ,           (8)

where n – power index.

Formula (7) is valid for a turbulent flow of the power fluid. Simplified approximation dependences were proposed for different ranges of power index n values [7]:

 

In the case of transporting high-viscosity oils, depressor additives and other treatment methods can be used [19-21], but they do not fully solve the arising complications.

The Leibenzon formula derived under the assumption λ=A/Rem, is written in general form as

0.5<n≤1.25    λ Re 1/4 =0.353n−3.80⋅ 10 −2 ;           (10)

where A, β and m – numerical coefficients depending on the mode of fluid motion; n – kinematic viscosity coefficient of oil; Q – volume flow of the pumped product.

The obvious advantage of Leibenzon formula is its analytical character, which allows clear linking the main parameters of pipeline transport - flow rate, viscosity, diameter and length of the pipeline with the head loss. This can then be used to analyze the methods for increasing carrying capacity, etc.

Work [35] (Table 1) proves the versatility of the Leibenzon formula for a wide nomenclature of pumped products and flow modes.

Despite a lot of work, at present, the formulas for analytical calculation of the high-viscosity oils motion in the form of the Leibenzon equation have been obtained only for a viscoplastic fluid.

Discussion

Leibenzon formula for a viscoplastic fluid:

h τ =β Q 2−m ν m 1+ τ 0 π d 3 6μQ m d 5−m L,             (13)

where μ – dynamic viscosity coefficient of fluid; τ0 – initial shear stress; the hydraulic slope can be represented as an expression

i=β Q 2−m ν m 1+ τ 0 π d 3 6μQ m d 5−m .              (14)

Coefficients of the Leibenzon formula at different flow modes:

β=4.5   s 2 /m,  m=1,   Re≤2.3⋅ 10 3 1+ I 6 ;            (15)
β=0.0247  s 2 /m,   m=0.25,    10 4 1+ I 6 ≤Re≤ 10 5 ;
β=0.089 Δ d 0.25 s 2 /m,    m=0,   Re>500 d Δ ,

where I  – Ilyushin number, I = τ0/mn, characterizes the ratio of the initial shear stress to the viscous friction stress; ∆ – absolute roughness of the pipe walls.

Table 1

Coefficients in the generalised Lebenzon formula for calculations during pumping of oil and petrole um products, natural gas and liquefied gases

Notes.
1. $\overline{k}$ - the relative roughness value of the pipline.
2. In laminar mode - except for piplines transporting fluids with anti-turbulence additives [12].
3. In turbulent mode -when pupming oil, petroleum products and liquefied hydrocarbon gases without anti-turbulence additives ƒ(θ)=1 [6].

In laminar mode, Metzner – Reed formula is used for calculating the hydraulic resistance coefficient of the power fluid [33]:

λ= 64 Re MR  ,            (16)

where ReMR  – generalized Reynolds number, determined by the formula

Re MR = ρ u (2−n) d n 8 n−1 k 3n+1 4n n  ,            (17)

u – oil flow velocity; k – consistency index of a power fluid.

Irwin suggested using the following dependence to determine the hydraulic resistance coefficient in the turbulent flow of a power fluid [2, 7]:

λ=4 D(n) Re MR 1 3n+1 ,            (18)
D n = 2 n+4 7 7n 4n 3n+1 3 n 2 .            (19)

The critical Reynolds number is proposed to be determined according to the Ryan-Johnson relation

Re MR = 6464n 3n+1 2 (2+n) 2+n 1+n  .             (20)

Formula (17) can be rewritten according to the dependence used by Leibenzon in deriving his formula,

λ= A Re MR m *  .            (21)

Then the power index of Reynolds number will be defined as

m * = 1 3n+1  .           (22)

Coefficient A in formula (21) is calculated based on the dependence

A=4D n 1 3n+1 .            (23)

The graph for the dependence of the coefficient A on the power index n in the power law of fluid flow is shown in Fig.1.

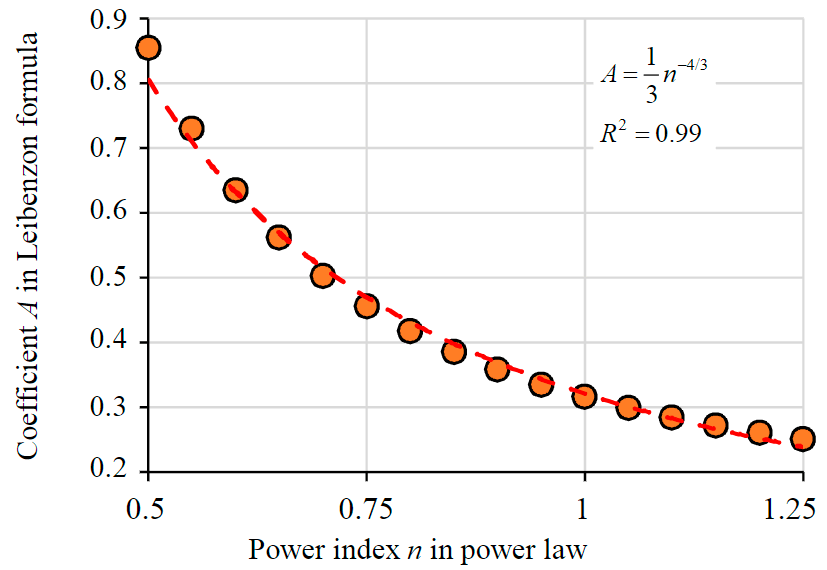
Fig.1. The graph for the dependence of the coefficient A on the power index n in the power law of fluid flow

As a result of regression processing of the data obtained, it was found that the coefficient A is described with sufficient accuracy by a relationship of the form:

A= n − 4 3 3  .           (24)

Let us begin the derivation of the modified Leibenzon formula for a power fluid by considering the conventional Darcy – Weissbach formula

h l =λ l d v 2 2g              (25)

and considering the oil flow rate is , we get an expression for friction losses in the oil pipeline

h l = Al⋅16 Q 2 Re MR m d2g π 2 d 4  .            (26)

Let us represent the generalized Reynolds number in a form convenient for further transformations:

Re MR m = ρ v 2−n d n 8 n−1 k 3n+1 4n n 1 3n+1 = ρ 4Q π d 2 2−n d n 8 n−1 k 3n+1 4n n 1 3n+1 = 4 2−n π 2−n 8 n−1 3n+1 4n n 1 3n+1 Q 2−n 3n+1 d 3n−4 3n+1 k ρ 1 3n+1  .              (27)

Then, taking into account expression (26), after a number of transformations, the expression for the friction losses will be written as:

h l = 16 n − 4 3 2g π 2 ⋅3 4 2−n 8 n−1 k 3n+1 4n n π 2−n 1 3n+1    l Q 2− 2−n 3n+1 k ρ 1 3n+1 d 5+ 3n−4 3n+1 =β l k ρ m Q 7n 3n+1 d 6−5m .              (28)

In expression (28) the coefficient β should be simplified, it is determined by the formula

β= 16 n − 4 3 2g π 2 ⋅3 4 2−n 8 n−1 k 3n+1 4n n π 2−n 1 3n+1 .              (29)

The graph for the dependence of the coefficient b on the power index n in the Leibenzon formula is shown in Fig.2, a

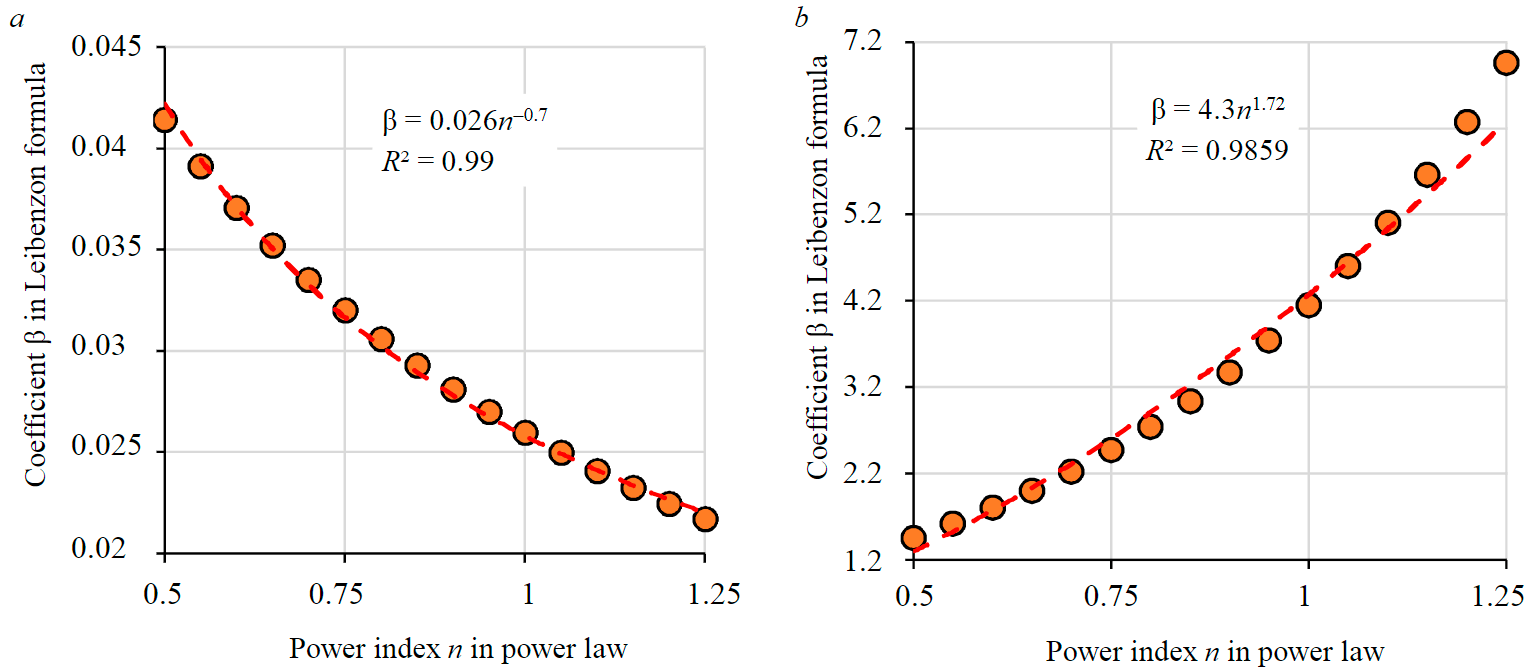
Fig.2. The graph for the dependence of the coefficient β on the power index n in the Leibenzon formula а – turbulent mode; b – laminar mode

Repeating the same data processing steps as with coefficient A, it was found that the coefficient β is described with sufficient accuracy by a dependence of the form:

$$ β=0.026 n −0,7 .               (30)

Finally, we obtain a modified Leibenzon equation for the head loss of a power fluid during turbulent motion in a pipeline, true for a range of power indices 0.5 ≤ n ≤ 1.25,

h=β l k ρ m Q 7 3 1−m d 6−5m  .                 (31)

Following the same reasoning logic, let us repeat the actions for laminar mode of power fluid flow. For this case the graph for dependence of coefficient on power index n in Leibenzon formula is shown in Fig.2, b.

Coefficients A = 64 and m = 1 for the laminar mode of the power fluid flow obviously follow from the dependence (21).

Summary of the obtained coefficients is shown in Table 2.

Table 2

Summary of the results obtained by the modified Leibenzon formula for a power fluid

Flow mode

Range applicability

Dependence for measuring of the head loss along the length

A

β, s2/m

m*

Turbulent

0.5 ≤ n ≤ 1.25

(relative error of results in the specified range does not exceed 2 %)

 
h=β l k ρ m * Q 7 3 1− m * d 6−5 m *
n − 4 3 3
0.026 n −0.7
1 3n+1

Laminar
h=β l k ρ Q n d 3n+1

64
$$ 4.3 n 1.7

1

The following conclusion can be made with regard to the Table 2: coefficient β in laminar flow mode at n → 1 is close to that in Stokes formula for Newtonian fluid (β = 4.15), and in turbulent flow – to Blasius formula (β = 0.0246). Artificial adjustment of coefficient to give formulas conceptual completeness is obviously possible, but entails increase of their error by 5 %.

Improvement of hydraulic efficiency is one of the main tasks in the field of pipeline oil transport [2, 13, 14]. Pipeline operation, as a rule, is accompanied by changes in pumping mode. If the increase of pumping parameters (flow rate, oil temperature) is within the limits of design values, the pipeline operation does not cause concerns, but if this increase is higher than the design values, it is necessary to check the “hot” pipeline for durability and stability (line part and piping of stations), as well as to specify conditions of pump operation for suction, leakage, temperature mode. In the first years of oil field development, the amount of oil produced is less than when it is fully loaded. With the development of the field the volume of pumped oil may be increased, in this regard, it is necessary to provide additional technical solutions to improve the efficiency of the produced oil transportation.

Let us consider theoretical justification of looping installation as an effective way to increase efficiency of high-viscosity oil transportation. Hydraulic slope of the pipeline pumping power fluid,

i p =β k ρ m * Q 7 3 (1− m * ) d p 6−5 m * .            (32)

The flow rate of the fluid in the pipeline is defined as

Q p = i p d p 6−5 m * k ρ m * β 7 3 (1− m * ) .             (33)

Flow rate in the looping can found in the same way:

Q l = i l d l 6−5 m * k ρ m * β 7 3 (1− m * ) .              (34)

The total flow rate in the pipeline is the sum of the flow rates in the main pipeline and the looping:

Q= Q l + Q p =Q= i l k ρ m * β 7 3 (1− m * ) d p 6−5 m * 7 3 (1− m * ) + d l 6−5 m * 7 3 (1− m * ) .               (35)

Let us transform the expression (33):

Q 7 3 (1− m * ) = i l k ρ m * β d p 6−5 m * 7 3 (1− m * ) 1+ d l d p 6−5 m * 7 3 (1− m * ) 7 3 (1− m * ) .                (36)

The hydraulic slope for looping is expressed as

i l =β k ρ m * Q 7 3 (1− m * ) d 6−5 m * 1 1+ d l d p 6−5 m * 7 3 (1− m * ) 7 3 (1− m * ) =iω .            (37)

Finally we get the coefficient that takes into account the presence of looping,

ω т * = 1 1+ D l D p 6−5 m * 7 3 (1− m * ) 7 3 (1− m * ) .             (38)

For low-viscosity oils this ratio is written as

ω= 1 1+ D l D p 5−m 2−m 2−m .             (39)

Coefficient for increase of carrying capacity

χ l = 1 1− l l L p 1−ω 1 2−m .              (40)

Comparing the values of the coefficients, taking into account the presence of looping, we obtain a graph of dependences series (Fig.3).

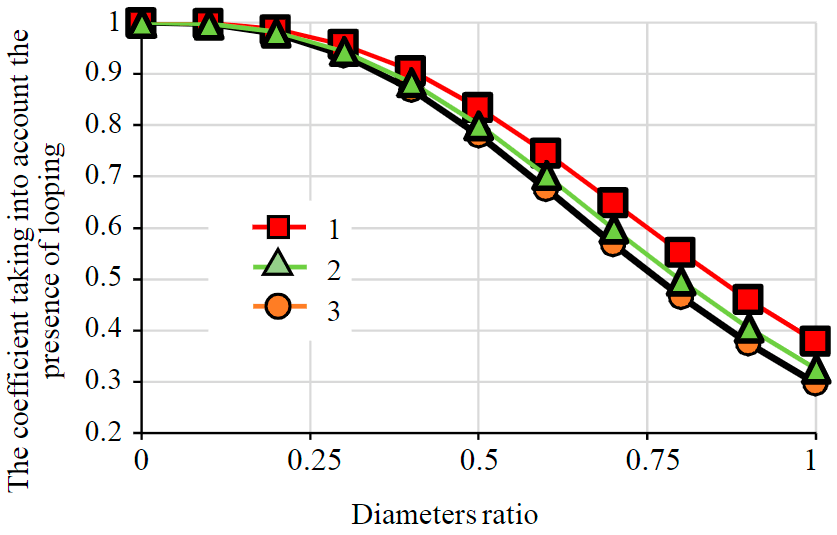
Fig.3. Graph for the dependence of the coefficient taking int account the presence of looping, on the diameters ratio for different types of oils 1 – Newtonian fluid (n = 1); 2 – power fluid (n = 0.5); 3 – power fluid (n = 0.75)

Several conclusions can be drawn from Fig.3:

  • the maximum difference is achieved at a ratio of diameters equal to one, and at the most distinct deviation from the Newtonian character of fluid flow;
  • due to insignificant difference of the coefficient, which takes into account the presence of looping (at n= 0.75 and Dl/Dp = 1 is not more than 10%), one can assume that when observing other technical solutions in terms of ensuring thermal mode, the coefficient for increase of carrying capacity will be close to the factor for low-viscosity oils.

Presented calculations on justification of looping are made on the basis of obtained modified Leibenzon formula and take into account properties of the power fluid. Graph in Fig.3 shows that difference of coefficient, considering looping presence for Newtonian and power fluid is insignificant (less than 10 %), which allows making conclusions about efficiency of looping application as means for increase of carrying capacity during the development of the field.

Conclusion

The calculation and justification of the modified Leibenzon formula for a viscoplastic fluid have been performed, which will allow developing a mathematical model for the operation of a cyclic oil pipeline transporting high-viscosity oil.

It was found that hydraulic calculation of oil pipelines transporting oil, the rheological properties of which are described by a power law, can be performed by the modified Leibenzon formula in the range 0.5 ≤ n ≤ 1.25. The relative error of the obtained ratio does not exceed 2%. It is important to note that the coefficients in the obtained formulas in the ultimate case of n = 1 are close to those of Newtonian oils, which indicates the internal unity of the obtained dependences.

Taking into account the obtained dependences, a theoretical justification for improving the performance of oil pipelines transporting high-viscosity oil by looping installation is presented.

References

  1. Mitusova T.N., Kondrasheva N.K., Lobashova M.M. et al. Influence of Dispersing Additives and Blend Composition on Stability of Marine High-Viscosity Fuels. Journal of Mining Institute. 2017. Vol. 228, p. 722-725. DOI: 10.25515/PMI.2017.6.722
  2. Nikolaev A.K., Pshenin V.V., Zakirov A.I., Zaripova N.A. Choice of Optimal Parameters of Bituminous Oil Transportation on the Example Ashalchinsky Field. Equipment and Technologies for Oil and Gas Complex. 2017. N 1, p. 53-59 (in Russian).
  3. Didkovskaya A.S., Lurie M.V. Iterative Algorithm of Hydraulic Calculation of the Non-Isothermal Oil Transfer. Science аnd Technologies: Oil and Oil Products Pipeline Transportation. 2016. N 2 (22), p. 50-55 (in Russian).
  4. Didkovskaya A.S., Lurie M.V. A Universal Algorithm for Numerical Calculations of Stationary Modes of the Pipelines. Science аnd Technologies: Oil and Oil Products Pipeline Transportation. 2015. N 4 (20), p. 85-91 (in Russian).
  5. Dolgii I.E. Methods to Enhance Oil Recovery in the Process of Complex Field Development of the Yarega Oil and Titanium Deposit. Journal of Mining Institute. 2018. Vol. 231, p. 263-267. DOI: 10.25515/PMI.2018.3.263
  6. Zholobov V.V., Sinelnikov S.V., Ignatenkova A.I. The Prospects of Dra for Reducing the Energy Consumption of Thermal Stations in a “Hot” Pumping. Science аnd Technologies: Oil and Oil Products Pipeline Transportation. 2019. Vol. 9. N 3, p. 256-265. DOI: 10.28999/2541-9595-2019-9-3-256-265 (in Russian).
  7. Zakirov A.I. Justification of modes for pipeline transport of bituminous oil: Avtoref. dis. … kand. tekhn. nauk. St. Petersburg: Sankt-Peterburgskiy gornyy universitet, 2016, p. 20 (in Russian).
  8. Aralov O.V., Buyanov I.V., Savanin A.S., Iordansky E.I. Research of Methods for Oil Kinematic Viscosity Calculation in the Oil-Trunk Pipeline. Science аnd Technologies: Oil and Oil Products Pipeline Transportation. 2017. Vol. 7. N 5, p. 97-105 (in Russian).
  9. Kislitsyn M.S., Yaroshenko V.V. Prospects of oil mining at Yarega field. Mining Informational and Analytical Bulletin. 2018. N 1, p. 12-18. DOI: 10.25018/0236-1493-2018-1-0-12-18 (in Russian).
  10. Kondrasheva N.K., Baitalov F.D., Boitsova A.A. Comparative Assessment of Structural-Mechanical Properties of Heavy Oils of Timano-Pechorskaya Province. Journal of Mining Institute. 2017. Vol. 225, p. 320-329. DOI: 10.18454/PMI.2017.3.320
  11. Lurie M.V. Computation Algorithm of Quasi-Steady-State Modes of Nonisothermal Oil Pumping. Oil and Oil Products Pipeline Transportation. 2014. N 2 (14), p. 28-31 (in Russian).
  12. Katsal I.N., Lyapin A.Yu., Dubovoy E.S. et al. On the Formation of Oil Traffic in Oil Trunk Pipelines System of JSC Transneft. Science аnd Technologies: Oil and Oil Products Pipeline Transportation. 2016. N 2 (22), p. 92-95 (in Russian).
  13. Revel-Muroz P.A., Fridlyand Ya.M., Kutukov S.E., Golyanov A.I. Assessing the Hydraulic Efficiency of Oil Pipelines According to the Monitoring of Process Operation Conditions. Science аnd Technologies: Oil and Oil Products Pipeline Transportation. 2019. Vol. 9. N 1, p. 8-19. DOI: 10.28999/2541-9595-2019-9-1-8-19
  14. Revel-Muroz P.A., Fridland Ya.M., Kutukov S.E. et al. Estimation of the Oil Pumping Technology Effectiveness with Drag Reduction Agents. Oil Industry. 2020. N 1, p. 90-95. DOI: 10.24887/0028-2448-2020-1-90-95 (in Russian).
  15. Rushd S., Rahman A. A Study on Friction Loss and Holdup Ratio in the Water Lubricated Pipeline Transportation of Heavy Oil. Science аnd Technologies: Oil and Oil Products Pipeline Transportation. 2019. Vol. 9. N 2, p. 200-206. DOI: 10.28999/2541-9595-2019-9-2-200-206 (in Russian).
  16. Semin S.L., Fedorov P.V. Optimization of Main Pipeline Process Parameters with Operating Oil Heating Stations and Anti-Turbulent Additives. Science аnd Technologies: Oil and Oil Products Pipeline Transportation. 2018. Vol. 8. N 6, p. 650-655 (in Russian).
  17. Sunagatullin R.Z., Karimov R.M., Dmitriev M.E., Baykova M.I. Experimental Studies of the Operational Properties of Asphaltene-Resin-Paraffin Deposits Formed in Main Oil Pipelines. Science аnd Technologies: Oil and Oil Products Pipeline Transportation. 2018. Vol. 8. N 4, p. 398-406. DOI: 10.28999/2541-9595-2018-8-4-398-406
  18. Surikov V.I., Shiryaev A.M., Lukmanov M.R. et al. About the Research of the Thermal and Ultrasonic Fields Influence on the Rheological Characteristics of High-Viscosity Oils. Science аnd Technologies: Oil and Oil Products Pipeline Transportation. 2015. N 2 (18), p. 21-25 (in Russian).
  19. Fedorov V.T., Kazakov V.V., Tchelinzew S.N. Technological Development in Application of a Depressor Additive in the Condition if High Viscous Oil Blend Transportation in Timano-Pechorskaya Oil-And-Gas-Bearing Province. Science аnd Technologies: Oil and Oil Products Pipeline Transportation. 2013. N 2 (10), p. 28-32 (in Russian).
  20. Fedorov P.V., Lukmanov M.R. Impact of Rheological Properties of Oil On Pipeline Operation Energy Efficiency. Science аnd Technologies: Oil and Oil Products Pipeline Transportation. 2020. Vol. 10. N 1, p. 8-16. DOI: 10.28999/2541-9595-2020-10-1-8-16 (in Russian).
  21. Fedorov P.V., Nekuchaev V.O., Pyustin A.A. Study of the Heat Treatment Influence on the Rheological Characteristics of High-Viscosity Oils. Science аnd Technologies: Oil and Oil Products Pipeline Transportation. 2016. N 6 (26), p. 58-63 (in Russian).
  22. Huayi Jiang, Bo Сао. Composition аnd Property Change of Heavy High-Viscosity Oil under the Influence of Microwave Radiation. Science аnd Technologies: Oil and Oil Products Pipeline Transportation. 2013. N 4 (12), p. 20-25 (in Russian).
  23. Huayi Jiang, Bo Сао. Evaluation of Temperature Distribution in Microphysical Model of Heavy Oil under the Influence of Microwave Radiation. Science аnd Technologies: Oil and Oil Products Pipeline Transportation. 2014. N 1 (13), p. 48-52 (in Russian).
  24. Cherepovitsyn А.Е., Lipina S.А., Evseeva О.О. Innovative Approach to the Development of Mineral Raw Materials of the Arctic Zone of the Russian Federation. Journal of Mining Institute. 2018. Vol. 232, p. 438-444. DOI: 10.31897/PMI.2018.4.438
  25. Sunagatullin R.Z., Karimov R.M., Tashbulatov R.R., Mastobaev B.N. Modeling the Thermal-Hydraulic Effect of Wax Layer. Science аnd Technologies: Oil and Oil Products Pipeline Transportation. 2019. Vol. 9. N 2, p. 158-162. DOI: 10.28999/2541-9595-2019-9-2-158-162 (in Russian).
  26. Abarasi Hart. A review of technologies for transporting heavy crude oil and bitumen via pipelines. Journal of Petroleum Exploration and Production Technology. 2014. Vol. 4. Iss. 3, p. 327-336. DOI: 10.1007/s13202-013-0086-6
  27. Alexandrov V.I., Vasilyeva M.A. Express-diagnosis of the technical state slurry pumps in systems hydrotransport processing tails of ore. Innovation-Based Development of the Mineral Resources Sector: Challenges and Prospects – 11th conference of the Russian-German Raw Materials, 7-8 November 2018, Potsdam, Germany. CRC Press, 2018, p. 273-282.
  28. Aleksandrova T.N., Romashev A.O., Aleksandrov A.V. About modeling of rheological properties of heavy oil suspensions. Oil Industry. 2016. Vol. 2016. Iss. 5, p. 68-70.
  29. Dejan Brkić. Review of explicit approximations to the Colebrook relation for flow friction. Journal of Petroleum Science and Engineering. 2011. Vol. 77. Iss. 1, p. 34-48. DOI: 10.1016/j.petrol.2011.02.006
  30. Nikitin M., Saychenko L. The rheological properties of abnormally viscous oil. Petroleum Science and Technology. 2017. Vol. 36. Iss. 2, p. 136-140. DOI: 10.1080/10916466.2017.1410558
  31. Palaev A.G., Shammazov I.A., Dzhemilev E.R. Research of the impact of ultrasonic and thermal effects on oil to reduce its viscosity. Journal of Physics. 2020. Vol. 1679 (5). DOI: 10.1088/1742-6596/1679/5/052073
  32. Saniere A., Henaut I., Argillier J.F. Pipeline transportation of heavy oils, a strategic, economic and technological challenge. Oil & Gas Science and Technology. 2004. Vol. 59. Iss. 5, p. 455-466. DOI: 10.2516/ogst:2004031
  33. Shangaraeva L., Klimko V. The application of the thermal stimulation in heavy oil recovery. Petroleum Science and Technology. 2016. Vol. 34. Iss. 23, p. 1894-1898. DOI: 10.1080/10916466.2016.1238934
  34. Smirnova N.N., Izotov E.A. Methodology for estimating heat losses due to heat effects on a heterogeneous oil reservoir. Journal of Industrial Pollution Control. 2018. Vol. 33. Iss. 1, p. 950-958.
  35. Valiev M.I., Korshak A.A. The use of the generalized formula of L.S.Leibenzon in the hydraulic calculation of pumping oil and petroleum products with small additives of polymers. Oil Industry. 2020. Vol. 2020. Iss. 8, p. 110-112. DOI: 10.24887/0028-2448-2020-8-110-112
Access statistics
Abstract Views
1464
Full-Text Views
196
Cited
Scopus:
11
Crossref:
8
Cited By
1. Predicting Service Life of Polyethylene Pipes under Crack Expansion using "Random Forest" Method. International Journal of Engineering Transactions C: Aspects. December 2023, Vol. 36, P. 2243-2252. DOI: 10.5829/ije.2023.36.12c.14 [Scopus] (cited: 4)
2. Standalone power system with photovoltaic and thermoelectric installations for power supply of remote monitoring and control stations for oil pipelines. Renewable Energy Focus. December 2023, Vol. 47, DOI: 10.1016/j.ref.2023.100493 [Scopus] (cited: 1)
3. Development of the automated temperature control system of the main gas pipeline. Scientific Reports. December 2023, Vol. 13, DOI: 10.1038/s41598-023-29570-4 [Scopus] (cited: 23)
4. Study of the Rheological Properties and Flow Process of High-Viscosity Oil Using Depressant Additives. Energies. September 2023, Vol. 16, DOI: 10.3390/en16176296 [Scopus] (cited: 3)
5. Numerical Simulation of Nonlinear Processes in the “Thruster—Downhole Motor—Bit” System While Extended Reach Well Drilling. Energies. May 2023, Vol. 16, DOI: 10.3390/en16093759 [Scopus] (cited: 1)
6. THE COMPREHENSIVE REVIEW OF PRACTICAL APPROACHES OF WOE SEPARATION BASED ON MAGNETIC IMPACT. SOCAR Proceedings. 2023, P. 158-172. DOI: 10.5510/OGP2023SI200906 [Scopus]
7. The role of multi-phase metal content in corrosion and premature failure mitigation of steel equipment in oil refineries. Part 1. CIS Iron and Steel Review. 2023, Vol. 25, P. 90-96. DOI: 10.17580/cisisr.2023.01.15 [Scopus] (cited: 1)
8. Development of a Numerical Method for Calculating a Gas Supply System during a Period of Change in Thermal Loads. Energies. January 2023, Vol. 16, DOI: 10.3390/en16010060 [Scopus] (cited: 20)
9. Modern Bitumen Oil Mixture Models in Ashalchinsky Field with Low-Viscosity Solvent at Various Temperatures and Solvent Concentrations. Energies. January 2023, Vol. 16, DOI: 10.3390/en16010395 [Scopus] (cited: 17)
10. Study of the Pipeline in Emergency Operation and Assessing the Magnitude of the Gas Leak. Energies. July 2022, Vol. 15, DOI: 10.3390/en15145294 [Scopus] (cited: 11)
11. INFLUENCE OF MAGNETIC-ABRASIVE PROCESSING ON ROUGHNESS OF FLAT PRODUCTS MADE OF AMTS GRADE ALUMINUM ALLOY. Tsvetnye Metally. 2022, Vol. 2022, P. 82-87. DOI: 10.17580/tsm.2022.07.09 [Scopus] (cited: 12)
Article Menu
Substantiation of analytical dependences for hydraulic calculation of high-viscosity oil transportation

Similar articles

Potential technological solution for sampling the bottom sediments of the subglacial lake Vostok: relevance and formulation of investigation goals
2021 Aleksei V. Bolshunov, Nikolay I. Vasiliev, Igor P. Timofeev, Sergey A. Ignatiev, Dmitriy A. Vasiliev, German L. Leichenkov
Innovative ways to control dust and explosion safety of mine workings
2021 Sergey B. Romanchenko, Yuri K. Naganovskiy, Anton V. Kornev
Possibilities of accounting the fracturing of Kashiro-Vereyskian carbonate objects in planning of proppant hydraulic fracturing
2021 Alexander S. Votinov, Valeriy V. Seredin, Igor Yu. Kolychev, Sergey V. Galkin
Indicator role of rare and rare-earth elements of the Northwest manganese ore occurrence (South Africa) in the genetic model of supergene manganese deposits
2021 Aleksandr N. Evdokimov; Benedict L. Pharoe
Regularities of electrochemical cleaning of oil-contaminated soils
2021 Nikolay S. Shulaev, Valeriya V. Pryanichnikova, Ramil R. Kadyrov
Development of a methodology to assess the hydrocyclone process with account of the rheological properties of the mineral slurry
2021 Tatiana N. Aleksandrova, Vadim A. Potemkin