Моделирование процессов деформирования и разрушения керна при его извлечении с больших глубин
- 1 — ассистент Санкт-Петербургский политехнический университет Петра Великого (СПбПУ) ▪ Orcid ▪ Elibrary ▪ Scopus ▪ ResearcherID
- 2 — канд. физ.-мат. наук доцент Санкт-Петербургский политехнический университет Петра Великого (СПбПУ) ▪ Orcid ▪ Elibrary ▪ Scopus ▪ ResearcherID
- 3 — д-р техн. наук профессор Санкт-Петербургский политехнический университет Петра Великого (СПбПУ) ▪ Orcid ▪ Elibrary ▪ Scopus ▪ ResearcherID
Аннотация
В статье проводится исследование изменения геофизических свойств горных пород в процессе подъема керна с больших глубин. Оценка изменения эффективных упругих свойств, пористости и проницаемости кернов при подъеме производилась путем конечно-элементного моделирования. На основе методов линейной механики разрушения произведена оценка критических размеров и ориентации внутренних дефектов, приводящих к разрушению керна при подъеме с больших глубин. Предложен подход, позволяющий оценить расчетным путем изменение механических свойств, пористости и трещиноватости пород-коллекторов в процессе подъема керна с глубин на поверхность. Использование уточненных данных о механических свойствах извлекаемых образцов пород позволяет повысить точность цифровых геологических моделей, необходимых при выполнении геологоразведочных работ, определении коллекторских свойств и нефте-, газонасыщенности месторождения, разработки залежей нефти и газа. Применение таких моделей является особенно актуальным на всех этапах при разработке месторождений с трудноизвлекаемыми запасами.
Введение
Из-за постепенного истощения традиционных месторождений нефти необходима разработка технологических решений для разведки и разработки месторождений с трудноизвлекаемыми запасами (ТРИЗ) [1], что накладывает дополнительные требования к точности геологических моделей. Это приводит к необходимости использования физико-механических, тектонофизических, геолого-геофизических свойств пород коллектора, соответствующих пластовым [12].
Большие глубины залегания (достигающие 3000 м) [1] пород-коллекторов ТРИЗ приводят к существенному изменению термобарических (PVT) условий при извлечении керна на поверхность. Это затрудняет определение реальных свойств пород коллектора в условиях, соответствующих пластовым. Снятие пластового давления при подъеме керна на поверхность приводит к повышению пористости и трещиноватости породы по сравнению с пластовыми условиями.
В то же время понижение температуры приводит к снижению пористости. Предварительная оценка физико-механических свойств горных пород в пластовых условиях может быть осуществлена на основе эффектов памяти [8] путем трехосного сжатия извлеченных кернов. В качестве критерия эквивалентности напряженно-деформированного состояния (НДС) керна в лабораторных и пластовых условиях могут служить эффекты памяти породы. Одним из наиболее известных является эффект Кайзера [10, 32], который заключается в невоссоздаваемости акустической эмиссии при циклическом нагружении для напряжений, меньших достигнутых ранее, и последующем резким возрастанием ее активности при превышении данного значения. Также различают ряд других эффектов: электромагнитный эмиссионный [16, 27], деформационный, ультразвуковой, электрический, магнитный [25], термоэмиссионный и др. [19, 31]. Однако исследования показали [8], что накопление поврежденности породы приводит к ухудшению проявления эффектов памяти, после чего возникает необходимость в развитии альтернативных методов.
В работе исследовалось изменение геофизических свойств горных пород при подъеме керна с больших глубин; выполнена оценка критических размеров внутренних дефектов, приводящих к разрушению керна при подъеме, с учетом их пространственной ориентации для различных уровней осевого и бокового давлений, действующих на керн. На основе данных экспериментов, выполненных в лабораторных условиях, предлагаемый подход позволяет уточнить физико-механические свойства горных пород в пластовых условиях, которые могут быть использованы для калибровки данных геофизических исследований.

Рис.1. Рассматриваемый керн: а – внешний вид;
б – данные КТ по 2D-срезам на разных высотах; в – распределение изолированных и связанных пор на внешней поверхности расчетной модели; г – внутренняя структура изолированных и связанных пор в КЭ модели
Постановка проблемы
Применение моделей деформирования керна, непосредственно учитывающих наличие пор, позволяет напрямую оценить изменение их объема при извлечении керна на поверхность. В качестве объекта исследования рассматривается цифровая модель керна, учитывающая его микроструктуру (рис.1). Построение трехмерной цифровой модели керна на основе данных компьютерной томографии (КТ) предполагает покадровую оцифровку данных КТ с целью преобразования совокупности попиксельных 2D-срезов исследуемого керна (рис.1, б) в цифровую 3D-модель с последующим сопоставлением отдельных вокселей 3D-модели с разработанной конечно-элементной (КЭ) моделью керна (рис.1, в). Данный подход позволяет достоверно, с учетом наличия микропор, построить КЭ модель для определения методом КЭ гомогенизации (рис.1) эффективных механических характеристик исследуемых нефтегазоматеринских пород.
В работе рассматривается имитационная модель керна, предполагающая наличие стохастически расположенных изолированных и связанных пор (рис.1, г). Разрешение цифровой модели составляет 750 mm. Предполагалось, что связанные поры располагаются вдоль ориентированных случайным образом линий. Объемная доля изолированных и связанных пор составляет по 2 % от общего объема керна. Рассматривался керн со следующими геометрическими характеристиками (рис.1, а): радиус R равен 15 мм, высота H – 80 мм.
Возрастающие требования к точности моделирования геомеханических процессов приводят к необходимости использования верифицированных моделей деформирования и разрушения горных пород. Сейчас применяется широкий спектр подходов к моделированию: метод конечных элементов (МКЭ) [3], метод подвижных клеточных автоматов [5, 20]; широкое применение получили подходы, основанные на молекулярной динамике [6, 24], перколяционные методы [29]. Необходимо выделить подходы, которые рассматривают геоматериалы как гомогенную среду; непосредственно, а также опосредованно учитывают наличие пор (например, с применением моделей пороупругости и поропластичности [21]). В данном исследовании для моделирования процессов деформирования и разрушения керна при его извлечении используется МКЭ в форме метода перемещений.
При глубоком залегании порода-коллектор находится в неоднородном вязко-упруго-пластическом состоянии. Причиной возникновения пластических (остаточных) деформаций является значительное весовое воздействие вышележащих пород. При извлечении керна наблюдается снятие нагрузки. Таким образом, для рассматриваемых условий нагружения допустимо решение краевой задачи в рамках неизотермической инфинитезимальной линейно-упругой постановки, которая использовалась в исследовании. В качестве отсчетной конфигурации рассматривалось состояние керна в пластовых условиях. Для определения напряженно-деформированного состояния при подъеме рассматривались вертикальное и боковое растягивающие давления, а также изменение температуры в объеме, что соответствует изменению термобарических условий при подъеме с больших глубин.
Процесс разгрузки керна при подъеме имеет двухстадийный характер. Сначала при обуривании керна горное давление сменяется на гидростатическое давление промывочной жидкости. Этот процесс заканчивается на расстоянии 1,0-1,5 диаметра керна от забоя скважины. Далее, во время подъема керн находится в условиях уменьшающегося равномерного всестороннего сжатия гидростатическим столбом промывочной жидкости. В итоге гидростатическое давление заменяется атмосферным. Использование принципа суперпозиции в рамках линейной постановки задачи позволяет не учитывать последовательность приложения нагрузок. Возможность применения этого подхода также подтверждается экспериментальными данными, полученными в работе [4]. Зависимость изменения открытой пористости от величины горного давления имеет ярко выраженный линейный характер.
Методология
Снятие сжимающих напряжений при подъеме моделировалось путем задания растягивающих вертикального и бокового давлений, изменение температуры задавалось отрицательным (охлаждение). Исходное вертикальное давление принималось равным 100 МПа, боковое – 30 МПа. В силу линейной постановки задачи результаты для других начальных термобарических условий могут быть получены линейным масштабированием полученных результатов. Например, для месторождения баженовского типа Большой Салым [9] исходное осевое давление равно 50 МПа, радиальное – 15 МПа.
При выполнении расчетов предполагалось, что и скелетный материал породы-коллектора, и эффективный материал пор являлись изотропными. В КЭ расчетах использовались параметры материалов [7]: скелет/поры – модуль Юнга 20/2 ГПа; коэффициент Пуассона 0,22/0,49; коэффициент теплового расширения 5∙10–6/2∙10–4 1/K.
Относительное изменение объема пор δр при подъеме пористого геоматериала на поверхность определяется в предположении малых деформаций первым инвариантом тензора деформаций ε:
где \(I^-_1(\epsilon)=\frac{1}{V_p} \int_{V_p}I_1(\epsilon)dV\) – осредненный по объему всех пор первый инвариант тензора деформаций; $I_1(\epsilon)=tr(\epsilon)=\epsilon_{11}+\epsilon_{22}+\epsilon_{33}$ – первый инвариант тензора, равный сумме его диагональных элементов.
Воспользовавшись декомпозицией тензора деформации на упругую εе и температурную εthсоставляющие, получаем зависимость:
Данные об изменении объема пор позволяют судить об изменении проницаемости горных пород на основе уравнения Козени – Кармана [13, 14]:
где k – проницаемость; φ – пористость; f – коэффициент формы сечения круглого капилляра; Sф – удельная поверхность фильтрующих каналов; Tг – гидравлическая извилистость каналов.
Связь между изменениями объема пор δр и пористости Δφ может быть выражена следующим образом:
Оценка параметров внутренних дефектов (а именно размеров и ориентации), приводящих к разрушению керна при подъеме, является актуальной задачей, требующей использования компьютерного моделирования процесса разрушения. Анализ условий распространения трещин выполнялся на основе методов линейной механики разрушения путем вычисления коэффициентов интенсивности напряжений (КИН) с использованием результатов конечно-элементного моделирования напряженного состояния кернов с трещинами различной начальной конфигурации.
Рассматривался случай керна с идеализированной центральной дискообразной трещиной (рис.2). Исследовались влияния радиуса трещины l и угла между плоскостью трещины и горизонтальной плоскостью a, и величины вертикального горного давления. Боковое давление во всех случаях нагружения задавалось пропорциональным вертикальному с коэффициентом 0,3. Определение напряженно-деформированного состояния керна с трещиной производилось в рамках линейно-упругой постановки. В рамках рассматриваемой модели макрооднородной среды изменение во времени однородного по пространству температурного поля не оказывает влияния на рост трещин. В связи с этим в исследовании такое изменение не учитывалось.
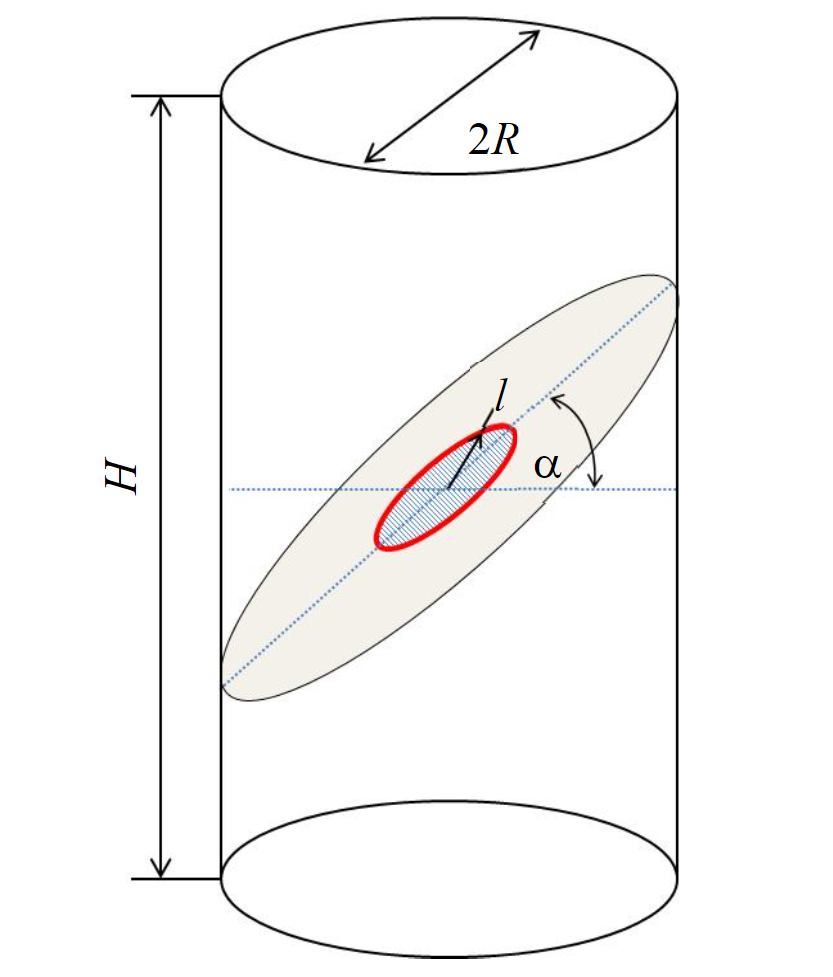
Рис.2. Геометрия керна с центральной дискообразной трещиной
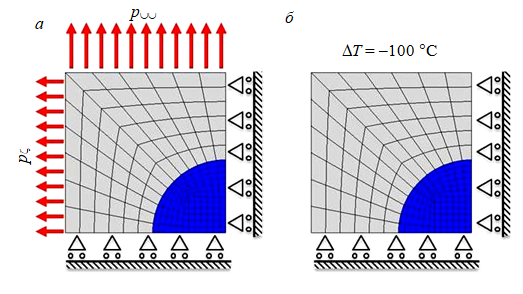
Рис.3. Граничные условия в модельных краевых задачах для элементарного представительного объема пористого материала при подъеме керна: изменение давления (а) и температуры (б)
Берега трещины рассматривались свободными. Определение КИН осуществлялось на основе анализа распределения полей перемещений в окрестности фронта трещины.
Сначала исследовалось влияние пространственной ориентации центральной внутренней дискообразной трещины в случае неизменности ее радиуса. Рассматривалось изменение угла между плоскостью трещины и горизонтальной плоскостью a в диапазоне от 0 до 45°. Радиус трещины l принимался равным 3 мм, радиус керна R – 15 мм (l/R = 0,2).
Все КИН (KI, KII и KIII) являются отличными от нуля. KII и KIII допускают изменение вдоль фронта трещины. В случае одновременного наличия нескольких мод разрушения (комбинация нормального отрыва, поперечного и продольного сдвигов) эффективный КИН Keff определялся по формуле, которая соответствует критерию скорости высвобождения энергии упругого деформирования [28]:
В случае горизонтальной трещины (α = 0°) KII и KIII равны нулю.
Рост трещины и, соответственно, разрушение керна начнется при условии Keff ≥ KIС, где KIС – критический КИН, характеризующий трещиностойкость материала.
Обсуждение
Определение изменения объема пор и пористости исследовалось для двух структурных уровней: (i) представительного объема с отдельной изолированной шарообразной порой в идеализированной периодической пористой структуре (рис.3) и (ii) непосредственно керна с учетом наличия изолированных и связанных пор (см. рис.1, в и г). Расчеты производились с помощью КЭ программного комплекса ANSYS. В расчетах использовались двадцатиузловые трехмерные изопараметрические КЭ с квадратичной аппроксимацией внутри КЭ полей узловых перемещений.
Первоначально оценивались изменения пористости грунта при подъеме на основе анализа относительного изменения объема изолированной шарообразной поры в идеализированной периодической структуре (рис.3).
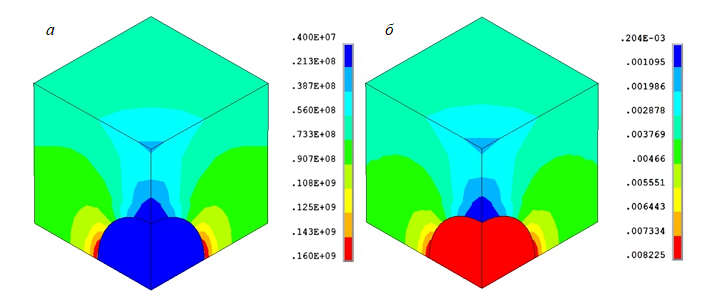
Рис.4. Распределение полей интенсивности напряжений (Па) (а) и деформаций (б) в элементарном представительном объеме пористого материала керна при подъеме
Задача решалась в трехмерной постановке. В силу симметрии рассматривалась 1/8 элементарного представительного объема (ЭПО) пористого материала в форме куба с центральной шарообразной порой с заданием условий симметрии на соответствующих гранях. К верхней грани прикладывалось растягивающее давление, соответствующее снимаемому вертикальному горному давлению р⊃, к боковым граням прикладывалось давление, соответствующее снимаемому боковому горному давлению рζ. Соотношение размеров ЭПО и шарообразных пор обеспечивают пористость, равную 4 %, что соответствует пористости пород-коллекторов баженовской свиты [15, 17, 18].
Путем КЭ моделирования подъема был определен вклад в изменение пор отдельных факторов: изменение давления и температуры. Так, снятие давления приводит к увеличению объема пор на 0,85 % по отношению к начальному объему, снижение температуры на 100 °С приводит к уменьшению объема пор на 0,2 %, что не противоречит [18]. На рис.4 представлены поля, характеризующие напряженное и деформированное состояния элементарного представительного
объема пористого материала керна, содержащего одиночную пору, при подъеме, характеризуемом изменением осевого давления на 100 МПа, бокового на 30 МПа и температуры на 100 °С. В качестве эффективной меры напряжений si и деформаций ei используется интенсивность по Мизесу:
где $\sigma_{ij}, \ \epsilon_{ij}, i,j=1,3$ – компоненты тензоров напряжений и деформаций; ν – коэффициент поперечной деформации.
Для оценки изменения объема нефтенасыщенных пор пород-коллекторов при их извлечении на поверхность выполнено прямое КЭ моделирование процессов деформирования керна с учетом его микроструктуры. Задача решалась со следующими граничными условиями: к верхней плоскости керна прикладывалось растягивающее давление, соответствующее снимаемому вертикальному горному давлению; к боковой грани (цилиндрической поверхности) – давление, соответствующее снимаемому боковому горному давлению. На нижней грани задано нулевое равенство осевых перемещений, а также закрепление центра нижнего сечения керна в двух направлениях в плоскости и фиксации еще одной степени свободы в направлении по образующей для точки на внешнем радиусе для исключения твердотельных (трансляционных и вращательных) движений. Модель содержит 328 704 КЭ. Исследования деформирования ЭПО показали, что изменение температуры не существенно влияет на изменение объема пор и в данной постановке оно не учитывалось.
Снятие горного давления при подъеме приводит к возрастанию объема пор на 1 %. Поля, характеризующие напряженно-деформированное состояние керна и отдельно для пор, представлены на рис.5.
Использование уточненных данных о механических свойствах извлекаемых образцов пород позволяет повысить точность цифровых геологических моделей. Одним из перспективных методов определения эффективных механических характеристик является метод КЭ гомогенизации, обеспечивающий эквивалентность энергий гетерогенной и гомогенной сред, выполненный с использованием данных о микропористой структуре пород, получаемых при помощи КТ.
Эффективные упругие свойства гомогенизированного материала керна определяются на основе равенства (обобщенный закон Гука):
где $^4C^-$ – тензор эффективных упругих податливостей 4-го ранга. Тензоры деформаций и напряжений, осредненные по объему представительного элемента, определяются следующими равенствами:
Черта над введенными тензорами означает соответствие гомогенизированному (осредненному) материалу.

Рис.5. Распределение полей интенсивности напряжений по Мизесу (Пa) (а) и интенсивности деформаций по Мизесу (б). Справа на каждом из рисунков показаны поля в порах
Упругие характеристики керна соответствуют анизотропному материалу. Модель трансверсально-изотропного материала с осью анизотропии вдоль направления вертикального весового воздействия может рассматриваться в качестве адекватного приближения. В качестве первого приближения, в предположении отсутствия влияния весового воздействия на формирование пор и изотропии свойств внепорового скелета, материал керна может рассматриваться как изотропный. В этом случае следствием уравнения (7) при одноосном растяжении для осевых компонент напряжений и деформаций справедлива простейшая связь
Для исследуемого керна (см. рис.1) рассчитано значение эффективного модуля Юнга материала: Eeff =19,2 ГПа.
При рассматриваемой величине пористости значение модуля Юнга, определенное при помощи КЭ гомогенизации, практически совпадает (разница менее 0,5 %) со значением, определяемым на основе правила смесей:
где Ep и Ek – модули упругости эффективного материала пор и скелета.
Однако применение данного правила возможно только при значениях пористости менее 10 %. При больших значениях увеличение диапазона возможных изменений упругих свойств гетерогенного материала керна (вилка Хилла [26]) приводит к существенным погрешностям в определении констант.
Предложенный подход может быть применен и при понижении разрешения цифровой модели керна. В этом случае требуется определение эффективных свойств укрупненных вокселей на основе модели с большим разрешением, что может быть выполнено при помощи КЭ гомогенизации.
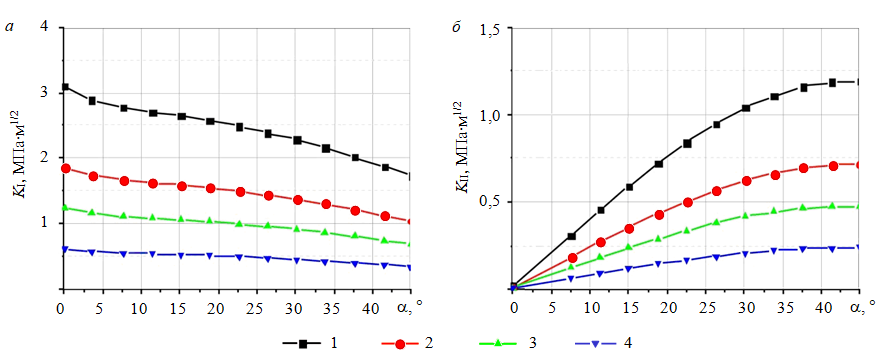
Рис.6. Зависимости КИН от угла наклона трещины (при l/R = 0,2) в керне KI(а), KII (б) для различных значений вертикального давления 1 – 50; 2 – 30; 3 – 20; 4 – 10 МПа
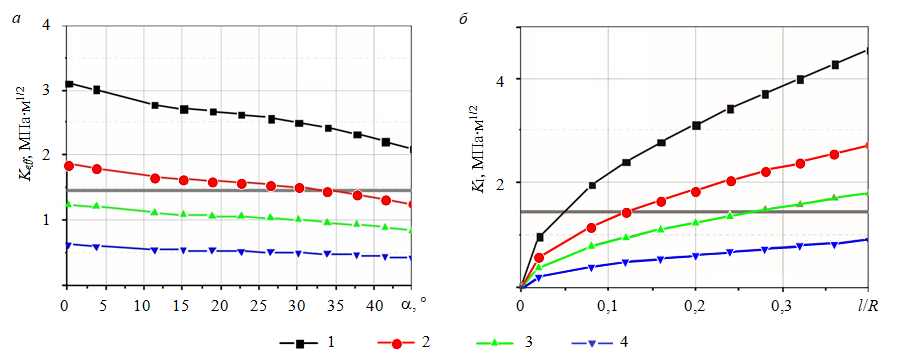
Рис.7. Зависимости Keff от угла наклона трещины в керне (l/R = 0,2) при различных уровнях осевого давления (а) и KI от относительного размера радиуса дискообразной внутренней горизонтальной (α= 0°) трещины в керне при различных уровнях осевого давления (б). Горизонтальная линия соответствует экспериментальному значению критического КИН KIС [11] 1 – 50; 2 – 30; 3 – 20; 4 – 10 МПа
Полученные результаты указывают на значительную степень неоднородности напряженного и деформированного состояний керна, вызванную изменением давления и температуры. Температура не оказывает значительного влияния на изменение объема пор. Сравнение результатов показало, что при эквивалентных термобарических условиях увеличение объема пор, определенное на основе полноразмерного керна с микропористой структурой, на 15 % больше, чем определенное на основе ЭПО керна с одиночной порой. Это объясняется тем, что в полноразмерной модели учитывается стохастическое (непериодическое) расположение пор, наличие связанной пористости и взаимного влияния пор друг на друга. На основе полученных результатов может быть произведена оценка упругих свойств материала керна и выполнен перерасчет эффективных упругих свойств отдельных компонент модели при понижении ее размерности.
При решении задач с трещиной материал керна принимался макрооднородным и изотропным. Определение эффективных упругих свойств керна проводилось методом конечно-элементной гомогенизации на основе разработанной цифровой модели керна.
Зависимости KI и KII от угла между плоскостью трещины и горизонтальной плоскостью a представлены на рис.6. В верхней и нижней точках фронта трещины (точки реализации максимального Keff) значение KIII равно нулю. При этом с ростом угла наклона трещины KI монотонно убывает, а KII монотонно возрастает.
Зависимость эффективного КИН Keff от угла отклонения плоскости трещины от горизонтали показана на рис.7, а. Коэффициенты KIС для пород-коллекторов изменяются в пределах
0,5-1,7 МПа·м1/2 [11]. В данном исследовании критическое значение КИН KIС принималось равным 1,46 МПа·м1/2, что соответствует значению трещиностойкости кернового материала газоконденсатного месторождения Аккум (Республика Казахстан). Сравнивая полученные зависимости Keff с KIС можно заключить, что для трещины радиусом 3 мм при осевом давлении 50 МПа разрушение наступает при любой ориентации трещины в пределах рассматриваемого диапазона. При давлении 30 МПа разрушение происходит при углах наклона трещины меньше 35°, при давлении меньше 20 МПа разрушение не происходит для трещин с любой ориентацией. Таким образом, для каждой ориентации трещины и ее радиуса может быть указана верхняя граница осевого давления (глубины залегания) ниже которой разрушение керна не происходит.
На следующем этапе исследовано влияние относительного размера трещины l/R на КИН в случае горизонтально ориентированной трещины (α = 0o). Рассматривалось изменение радиуса трещины в диапазоне от 3 до 12 мм. Для малых значений l/R, в предположении отсутствия бокового давления, полученные результаты показали хорошее соответствие с известным аналитическим решением для наклонной трещины в неограниченном пространстве [28]. Различие не превышает 0,5 %. Зависимость KI от относительного размера трещины представлена на рис.7, б. Ее анализ позволяет заключить, что при осевом давлении 50 МПа разрушение наступает при отношении l/R больше 0,05 (l > 0,75 мм), при давлении 30 МПа – больше 0,11, при 20 МПа – больше 0,29.
Обнаружение факта разрушения керна при поднятии с больших глубин несет информацию о превышении размеров дефекта критических значений, оценка которых может быть произведена на основе номограмм, аналогичных представленной на рис.7, б.
Полученные результаты позволяют качественно и количественно оценивать влияние различных факторов (размеров и ориентации внутренних дефектов, механических свойств материала, глубины залегания породы) на трещиностойкость кернов при подъеме с больших глубин на поверхность. Для уточнения результатов следует использовать методы нелинейной механики разрушения [2, 22] и более сложные модели материала [21, 23, 30].
Заключение
Предложен подход, позволяющий оценить изменение пористости и трещиноватости пород-коллекторов при извлечении керна на поверхность. Путем прямого конечно-элементного моделирования процессов деформирования керна оценивалось изменение объема нефтенасыщенных пор керна при его извлечении с глубины 2900 м, соответствующей месторождениям баженовского типа. С целью определения критических размеров и ориентации внутренних дефектов, приводящих к разрушению керна при подъеме, получены результаты моделирования процесса разрушения кернов с трещинами различной начальной конфигурации.
На основе результатов конечно-элементного анализа изменения напряженно-деформированного состояния керна получена зависимость изменения объема нефтенасыщенных пор от изменения термобарических условий при его подъеме с больших глубин.
В расчетах детально учитывалась микроструктурная неоднородность свойств керна на основе использования разработанной цифровой модели керна. Для определения эффективных свойств применялся метод конечно-элементной гомогенизации.
Получены и проанализированы результаты влияния размера и пространственной ориентации внутренней круговой трещины в керне на его разрушение при подъеме, найденные на основе результатов конечно-элементных расчетов с использованием критериев линейной механики разрушения. Представлены результаты влияния осевого и бокового давлений на критические значения размера трещины и угла отклонения нормали плоскости трещины от оси керна.
Литература
- Alekseev A. Palyanovskiy breakthrough. New results in the development of the Bazhenov formation resources. Sibirskaya neft. 2016. Vol. 136. N 9, p. 38-42 (in Russian).
- Astafev V.I., Radaev Yu.N., Stepanova L.V. Non-linear mechanics of destruction. Samara: Izd-vo “Samarskii universitet”, 2004, p. 562 (in Russian).
- Damaskinskaya E.E., Kuksenko V.S. Computer modeling of fracture of rocks. Vestnik Dalnevostochnogo gosudar-stvennogo tehnicheskogo universiteta. 2011. Vol. 3-4, p. 8-9 (in Russian).
- Durkin S.M., Trukhonin K.A. Numerical model of HVO filtration Improvement of informational support. Delovoi zhurnal Neftegaz.RU. 2019. N 11(95), p. 66-73 (in Russian).
- Konovalenko I.S., Smolin A.Yu., Psakhie S.G. Multilevel simulation of deformation and fracture of brittle porous materials using the method of movable cellular automata. Physical mesomechanics. 2009. Vol. 12. N 5, p. 29-36 (in Russian).
- Krivtsov A.M. Deformation and destruction of microstructured solids. Мoscow: Fizmatlit, 2007, p. 304 (in Russian).
- Kulyapin P.S., Sokolova T.F. Statistical well log analysis of the Bazhenov formation. Seismic Technologies. 2013. Vol. 3, p. 28-42 (in Russian).
- Lavrov A.V., Shkuratnik V.L., Filimonov Yu.L. Acoustic emission memory effect in rocks. Мoscow: Moskovskii gosudarstvennyi gumanitarnyi universitet, 2004, p. 437 (in Russian).
- Nesterov I.I., Stasyuk M.E., Storozhev A.D. Methodology for substantiating the initial formation pressure in the Bazhenov-type oil deposits (on the example of the Bolshoi Salym field). Geologiya nefti i gaza. 1985. N 8, p. 1-6 (in Russian).
- Nosov V.V. Control of inhomogeneous materials strength by method of acoustic emission. Journal of Mining Institute. 2017. Vol. 226, p. 469-479. DOI: 10.25515/PMI.2017.4.469
- Kashnikov Y.A., Ashikhmin S.G., Kukhtinskii A.E., Shustov D.V. The relationship of fracture toughness coefficients and geophysical characteristics of rocks of hydrocarbon deposits. Journal of Mining Institute. 2020. Vol. 241, p. 83-90. DOI: 10.31897/PMI.2020.1.83
- Galkin S.V., Krivoshchekov S.N., Kozyrev N.D. et al. Accounting of geomechanical layer properties in multi-layer oil field development. Journal of Mining Institute. 2020. Vol. 244, p. 408-417. DOI: 10.31897/PMI.2020.4.3
- Amosu A., Mahmood H., Ofoche P. Estimating the Permeability of Carbonate Rocks from the Fractal Properties of Moldic Pores using the Kozeny-Carman Equation. Research Ideas and Outcomes. 2018. Vol. 4. N e24430. DOI: 10.3897/rio.4.e24430
- Mirzaei-Paiaman А., Ostadhassan М., Rezaee R. et al. A new approach in petrophysical rock typing. Journal of Petroleum Science and Engineering. 2018. Vol. 166, p. 445-464. DOI: 10.1016/j.petrol.2018.03.075
- Christensen R. Mechanics of composite materials. New York: Courier Corporation, 2012, p. 384.
- Bespalko A.A., Yavorovich L.V., Eremenko A.A., Shtirts V.A. Electromagnetic Emission of Rocks after Large-Scale Blasts. Journal of Mining Science. 2018 Vol. 54, p. 187-193. DOI: 10.1134/S1062739118023533
- Gorshkov A.M., Kudryashova L.K., Van Khe L. Petrophysical rock properties of the Bazhenov Formation of the South-Eastern part of Kaymysovsky Vault (Tomsk Region). Problems of Geology and Subsurface Development: XX International Scientific Symposium of Students, Postgraduates and Young Scientists, 4-8 April 2016, Tomsk, Russia. IOP Conference Series: Earth and Environmental Science, 2016. Vol. 43. N 012010. DOI: 10.1088/1755-1315/43/1/012010
- Popov Е., Kalmykov A., Cheremisin A. et al. Laboratory investigations of hydrous pyrolysis as ternary enhanced oil recovery method for Bazhenov formation. Journal of Petroleum Science and Engineering. 2017. Vol. 156, p. 852-857. DOI: 10.1016/j.petrol.2017.06.017
- Lavrov A. Fracture-induced Physical Phenomena and Memory Effects in Rocks: A Review. Strain. 2005. Vol. 41, p. 135-149. DOI: 10.1111/j.1475-1305.2005.00233.x
- Levandovskiy A.N., Melnikov B.E., Shamkin A.A. Modeling of porous material fracture. Magazine of Civil Engineering. 2017. Vol. 69, p. 3-22. DOI: 10.18720/MCE.69.1
- Le-Zakharov S.A., Melnikov B.E., Semenov A.S. Nonlinear analysis of fluid saturated soil and rock under complex hydromechanical loading on the base of poroplastic models. Materials Physics and Mechanics. 2017. Vol. 31, p. 32-35.
- Nosikov A.I., Semenov A.S., Melnikov B.E., Rayimberdiyev T.P. Prediction of short fatigue crack propagation on the base of non-local fracture criterion. Proceedings of the XXVI International Conference Mathematical and Computer Simulation in Mechanics of Solids and Structures (MCM 2015), 28-30 September 2015, Saint Petersburg, Russia. Materials Physics and Mechanics, 2017. Vol. 31. Iss. 1-2, p. 44-47.
- Semenov A., Melnikov B. Interactive Rheological Modeling in Elasto-viscoplastic Finite Element Analysis. Procedia Engineering. 2016. Vol. 165, p. 1748-1756. DOI: 10.1016/j.proeng.2016.11.918
- Shilko E., Dudkin I., Grigoriev A. The development of the formalism of movable cellular automata for modeling the nonlinear mechanical behavior of viscoelastic materials. XXVI Conference on Numerical Methods for Solving Problems in the Theory of Elasticity and Plasticity (EPPS-2019), 24-28 June 2019, Tomsk, Russia. EPJ Web of Conferences, 2019. Vol. 221. N 01052. DOI: 10.1051/epjconf/201922101052
- Shkuratnik V.L., Lavrov A.V. Memory effects in rock. Journal of Mining Science. 1995. Vol. 31, p. 20-28. DOI: 10.1007/BF02046886
- Balushkina N.S., Kalmykov G.A., Belokhin V.S. et al. Siliceous reservoirs of the Bazhenov formation, the Sredny Nazym Oil Field, and the structure of their pore space. Moscow University Geology Bulletin. 2014. Vol. 69, p. 91-100. DOI: 10.3103/s0145875214020033
- Han J., Huang S., Zhao W. et al. Study on Electromagnetic Radiation in Crack Propagation Produced by Fracture of Rocks. Measurement. 2018. Vol. 131, p. 125-131. DOI:10.1016/j.measurement.2018.06.067
- Tada H. The stress analysis of cracks handbook. New York: ASME Press, 2000, p. 677.
- Tang Q., Zhou Y., Zhao D. Numerical simulation of deformation memory effect of rock materials in lowstress condition using discrete element method. Energy Science & Engineering. 2020. Vol. 8. Iss. 9, p. 3027-3046. DOI: 10.1002/ese3.719
- Benin A.V., Semenov A.S., Semenov S.G., Melnikov B.E. The simulation of bond fracture between reinforcing bars and concrete. Part 2. Models without taking the bond discontinuity into account. Magazine of Civil Engineering. 2014. Vol. 45, p. 23-40. DOI: 10.5862/MCE.45.4
- Vinnikov V.A., Shkuratnik V.L. Theoretical model for the thermal emission memory effect in rocks. Journal of Applied Mechanics and Technical Physics. 2008. Vol. 49, p. 301-305. DOI: 10.1007/s10808-008-0041-3
- Yulong C., Muhammad I. Experimental study of Kaiser effect under cyclic compression and tension tests. Geomechanics and Engineering. 2018. Vol. 14, p. 203-209. DOI: 10.12989/gae.2018.14.2.203
