Исследование токов привода подъема мостовых кранов металлургических предприятий для раннего диагностирования превышения массы груза
- 1 — д-р техн. наук Севастопольский государственный университет ▪ Orcid ▪ Elibrary ▪ Scopus ▪ ResearcherID
- 2 — канд. техн. наук Сибирский государственный индустриальный университет ▪ Orcid ▪ Elibrary ▪ Scopus
- 3 — АО «Сибирский Тяжпромэлектропроект» ▪ Orcid ▪ Elibrary
Аннотация
В статье рассматривается основанный на анализе токов приводного электродвигателя подход к созданию дополнительного средства защиты от аварийных ситуаций при эксплуатации мостовых кранов, связанных с подъемом груза массой, превышающей допустимую. Описана математическая модель привода мостового крана, а также результаты компьютерного моделирования. Показано, что в процессе подъема до начала этапа отрыва груза ток статора приводного электродвигателя от массы груза не зависит, но при отрыве груза уже за единицы периодов сетевого напряжения после натяжения каната при превышении массы гру за фиксируется поддающееся измерению превышение амплитудного значения тока. Данная закономерность подтверждена для ряда кранов различной грузоподъемности, применяемых на металлургических предприятиях. Продемонстрирована возможность диагностирования превышения массы поднимаемого груза с более высоким быстродействием, чем у существующих механических способов контроля перегрузки, при этом не требуется вносить изменения в конструктивные элементы мостовых кранов.
Введение. В число основных видов технологического и ремонтного оборудования на металлургических предприятиях входят грузоподъемные механизмы: мостовые краны и кран-балки различного назначения. Удельный вес грузоподъемных механизмов в составе технологического и ремонтного оборудования цехов металлургических предприятий может достигать 10-13 %. Аварии, связанные с использованием грузоподъемной техники, зачастую приводят к травматизму людей, оказавшихся в опасной зоне [3]. Кроме того, от надежной работы грузоподъемных механизмов зависит ритмичность технологических процессов и высокие экономические показатели предприятий. Поэтому обеспечение грузоподъемных механизмов современными быстродействующими средствами защиты от аварийных ситуаций и средствами диагностики является актуальной задачей [5, 14, 15].
Для мостовых кранов металлургических предприятий стандартными являются следующие аварийные ситуации: переподъем грузозахватного органа, нарушение целостности и геометрии элементов конструкции крана, обрыв подъемных канатов, перегрев и выход из строя электродвигателя подъема. К перечисленным аварийным ситуациям может привести увеличение нагрузки крана при подъеме груза недопустимой массы.
Для защиты от аварий, вызванных подъемом грузов недопустимой массы, используются ограничители грузоподъемности. В настоящее время применяются несколько способов контроля перегрузки, среди которых устройства с применением пружинно-рычажных систем [6] и устройства с использованием тензодатчиков [8, 9], которые, однако, не обладают достаточными точностью, чувствительностью и быстродействием. Также разработаны схемы защиты с применением дополнительных силовых элементов, однако они усложняют конструкцию грузоподъемных механизмов, снижая этим надежность защиты [7].
С учетом изложенного, а также в условиях сокращения персонала ремонтных и эксплуатирующих подразделений, для распознавания аварийного превышения массы груза необходимо использовать дополнительные возможности, в том числе методы косвенного контроля. Для косвенного контроля оборудования горно-металлургических предприятий используются методы, основанные на анализе изменения во времени параметров рабочего цикла [1], в том числе анализе динамического состояния приводных электродвигателей [11, 12].
Существуют методы косвенного контроля массы груза для управления и защиты кранового оборудования в процессе подъема для кранов иного назначения. Так в источниках [21, 23, 32] предлагаются системы мониторинга и диагностики для мобильного, башенного и мостового кранов соответственно, предоставляющие дополнительную информацию о работе крана его оператору. Однако все эти системы для определения массы груза предполагают использование в конструкции крана дополнительных датчиков – энкодеров, тензодатчиков. В статье [24] описана система управления для портового крана со встроенным контуром оценивания массы груза, для функционирования которого используются дополнительные датчики смещения груза относительно подъемного блока стрелы, однако в ней не предполагается возможность наличия слабины каната. В статье [28] показана система управления для подъемного крана буровой платформы, в которой масса груза вычисляется по данным тензодатчика подъемного каната и датчика гидродинамического давления. Работы [30, 31] рассматривают систему защиты от перегрузки при подъеме для кранов морского назначения в составе системы управления с упреждением, для функционирования которой используются совместно динамическая модель серводвигателя тяговой лебедки и подъемного механизма с грузом, однако отличия конструкции не позволяют переложить такой подход на мостовые краны металлургических предприятий.
Системы защиты от превышения массы груза с применением методов косвенного контроля для крановых механизмов применяются активно, однако эффективный подход для мостовых кранов, не требующий установки в механической подсистеме крана дополнительных датчиков, а использующий информацию о динамическом состоянии электродвигателей, в настоящее время отсутствует.
Постановка проблемы. Для создания дополнительного средства предотвращения аварийных ситуаций – подъема грузов недопустимой массы – с использованием контроля токов электродвигателя механизма подъема мостового крана необходимо проводить анализ его динамического состояния, а при анализе динамических режимов электроприводов горно-металлургического оборудования необходимо обязательно учитывать динамику механической подсистемы [4,]. Для механизмов подъема мостовых кранов разработан ряд математических моделей, описывающих динамические режимы и процессы в узлах и элементах оборудования [2, 19, 22, 27]. Однако эти модели очень сложны и поэтому не подходят для решения поставленной задачи, предполагая в последующем необходимость технической реализации в виде программно-аппаратного средства, для чего нужна относительно простая модель с сосредоточенными параметрами, но адекватно описывающая технологическую операцию подъема груза краном и позволяющая достоверно идентифицировать аварийную ситуацию превышения массы груза.
Операция подъема груза состоит из трех последовательных этапов, а именно выбора слабины каната до появления в нем усилия натяжения, натяжения каната до уравновешивания усилием в канате веса груза и отрыва груза с его последующим подъемом. Важной особенностью этапа выбора слабины каната является фактическое отсутствие взаимной связи между грузом и приводным электродвигателем до появления в канате усилия натяжения. Это значит, что диагностировать аварийное превышение массы груза косвенным методом возможно только в результате детального анализа математической модели электродвигателя привода подъема и кранового механизма при переходе от первого этапа ко второму и третьему, в ходе которого необходимо выявить диагностические признаки режима подъема груза чрезмерной массы.
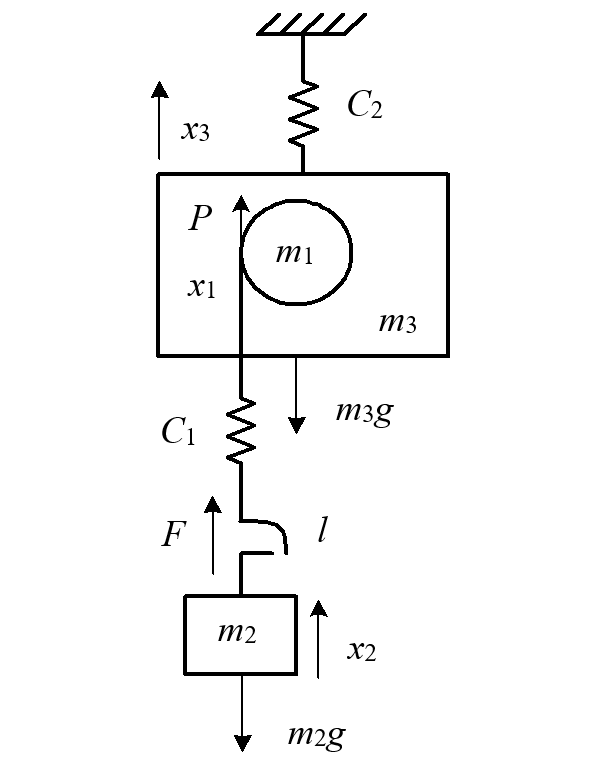
Методология. Для математического описания механизма привода подъема мостовых кранов наиболее распространенной на практике является модель трехмассовой механической системы с упругими связями между массами [25], представленная на рис.1, где m1, m2, m3 – приведенные к канату массы вращающихся частей механизма подъема, груза и моста; x1, x2, x3 – перемещения масс; C1, C2 – жесткости каната и моста крана; l – слабина каната; P – пусковая сила электродвигателя, определяемая как произведение электромагнитного момента на валу двигателя M на коэффициент приведения Kp = i/Rбар; F – усилие в канате.
На основании данной модели составляются системы дифференциальных уравнений, описывающие систему на этапах выбора слабины каната, его натяжения и отрыва груза от опоры [25]. Последовательное моделирование каждого из этапов с учетом начальных условий при переходе от одного к другому позволяет адекватно описать динамическое состояние механизма привода подъема мостовых кранов, а условия начала и окончания этапов приведены в таблице.
Условия начала и окончания этапов движения механизма подъема
| Этап | Начальные условия | Условия окончания |
| 1. Выбор слабины каната | $$ \begin{array} [c]{ll} x_1=0; \ x_2=0; \ x_3=0; \\ x_1^{'}=0; x_2^{'}=0; x_3^{'}=0; t=0; \end{array} $$ | $$ \begin{array} \biggl\ \begin{cases} x_{1}=l; \\ F=C_1(x_1-l)>0; \end{cases} \\ x_{11k}=x_1; \ x_{21k}=0; \ x_{31k}=x_3; \\ x_{11k}^{'}=x_1^{'}; \ x_{21k}^{'}=0; \ x_{31k}^{'}=x_3^{'}; \ t=t_{1k}.\end{array} $$ |
| 2. Натяжение каната до уравновешивания | $$ \begin{array} [c]{ll} x_1=x_{11k}; \ x_2=x_{21k}; \ x_3=x_{31k}; \\ x_1^{'}=x_{11k}^{'}; x_2^{'}=x_{21k}^{'}; x_3^{'}=x_{31k}^{'}; t=t_{1k}; \end{array} $$ | $$ \begin{array} [c]{ll} F=C_1(x_1-x_2)=m_2g; \\ x_{12k}=x_1; \ x_{22k}=0; \ x_{32k}=x_3; \\ x_{12k}^{'}=x_1^{'}; \ x_{22k}^{'}=0; \ x_{32k}^{'}=x_3^{'}; \ t=t_{2k}.\end{array} $$ |
| 3. Отрыв груза с последующим подъемом | $$ \begin{array} [c]{ll} x_1=x_{12k}; \ x_2=x_{22k}; \ x_3=x_{32k}; \\ x_1^{'}=x_{12k}^{'}; x_2^{'}=x_{22k}^{'}; x_3^{'}=x_{32k}^{'}; t=t_{2k}; \end{array} $$ | - |
Движение масс трехмассовой механической системы после отрыва груза описывается следующей системой уравнений:
Для последующего анализа систему уравнений удобно привести к линейному виду, выполнив замену переменных:
Данная система уравнений показывает, что электромагнитный момент двигателя M и масса груза m2 при переходе к этапам натяжения каната и отрыва груза оказываются динамически связанными, а значит анализ величин, влияющих на электромагнитный момент на этом этапе, способен выявить диагностические признаки режима подъема груза чрезмерной массы.
Систему уравнений (2) можно решить различными методами. Поскольку современные системы диагностики технически реализуются на базе микроконтроллерных устройств, для которых характерно квантование сигналов по времени, удобно привести систему уравнений (2) к дискретному виду. Для выполнения дискретизации используются последовательно преобразование Лапласа и билинейное преобразование (преобразование Тастина).
После перехода от пространства оригиналов к пространству комплексной переменной p, выполняя преобразование Лапласа, и далее от нее через билинейное преобразование к переменной z, получим следующую дискретную модель:
Система уравнений (3) должна решаться совместно с математической моделью электропривода, включая мостовой кран в состав электромеханического комплекса [13]. В качестве электропривода рассматривается привод на базе асинхронного двигателя.
Для составления математического описания асинхронного двигателя может быть использовано несколько подходов [16, 17, 26, 29]. Одним из них является моделирование в фазных координатах, которое наиболее соответствует задачам диагностирования, поскольку является более подходящим в случае неисправностей самого двигателя.
Асинхронный двигатель в фазных координатах a, b, c описывается системой дифференциальных уравнений [20]:
где UA, UB, UC – напряжения на зажимах обмотки статора; ΨA, ΨB, ΨC, iA, iB, iC – потокосцепления и токи обмоток фаз статора; rA, rB, rC – активные сопротивления обмоток фаз статора; Ψa, Ψb, Ψc, ia, ib, ic – потокосцепления и токи обмоток фаз ротора; ra, rb, rc – активные сопротивления обмоток фаз ротора; γ – угловое положение ротора; WЭМ – запас электромагнитной энергии машины; p – число пар полюсов; ωr – частота вращения ротора; ωs – синхронная частота вращения поля статора.
Потокосцепления статорных и роторных обмоток описываются следующими уравнениями:
где LA, LB, LC – индуктивности фаз статора; La, Lb, Lc – индуктивности фаз ротора; MAB, MBC, MAC – взаимные индуктивности между обмотками статора; Mab, Mbc, Mac – взаимные индуктивности между обмотками ротора.
Поскольку обмотки статора и ротора перемещаются относительно друг друга с частотой ωr, взаимные индуктивности между обмотками определяются гармоническими зависимостями [20], где MAam, MBbm, MCcm – максимальные значения взаимной индуктивности при прохождении обмотками ротора фаз a, b и с соответственно точно под обмотками статора фаз А, В и С. Например, для фазы А:
В результате дифференциальная трехфазная модель асинхронного электродвигателя в естественных фазных координатах, полученная из системы уравнений (4), выглядит следующим образом:
где производные зависимых от угла γ потокосцеплений определяются путем дифференцирования системы уравнений (5) по времени как сложной функции с учетом гармонических зависимостей взаимной индуктивности (6) для фазы А и аналогичных им для фаз В и С.
Систему уравнений (7), аналогично модели трехмассовой механической системы, посредством билинейного преобразования [10] удобно представить в дискретной форме:
где матрицы напряжений и токов:
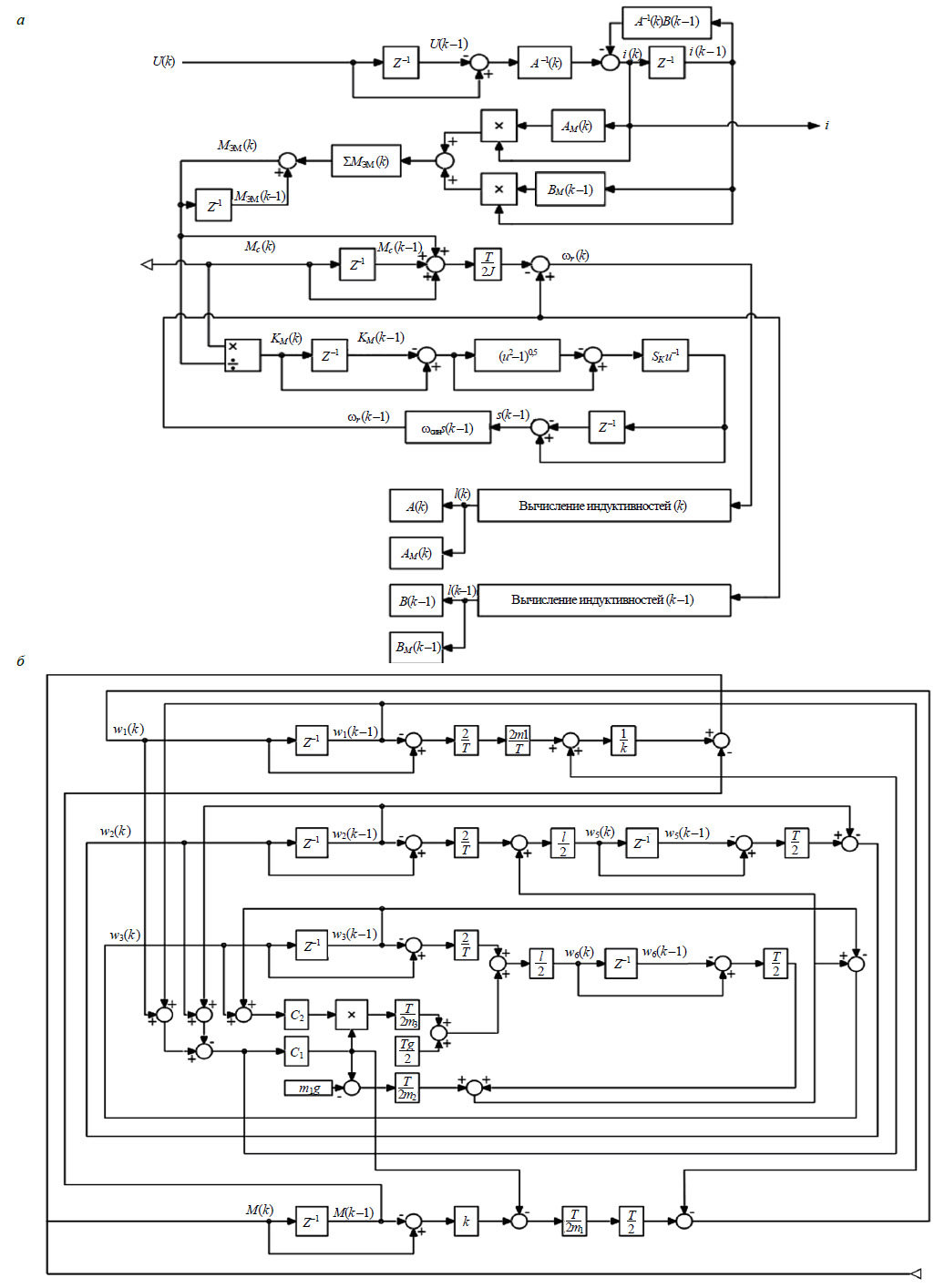
Аналитическое решение задач Коши для этапов подъема груза с использованием полученного описания электродвигателя и трехмассовой механической системы представляется затруднительным ввиду наличия большого количества переменных, а также производной по углу поворота ротора, в связи с чем полученное математическое описание анализировалось методом компьютерного моделирования в программном комплексе Matlab Simulink [18]. Модель привода подъема мостового крана, соответствующая уравнениям (2)-(9), показана на рис.2.
Обсуждение. Покажем использование приведенной на рис.2 модели для расчетов токов статора двигателя механизма подъема ремонтного мостового крана грузоподъемностью 32 т. Система моделировалась в режимах подъема груза номинальной массы и подъема груза массой, превышающей допустимую на 3, 15 и 25 %, соответственно при проведении вычислительных экспериментов в качестве массы груза m2 в системе уравнений (3) были заданы следующие значения: mI = 32000 кг, mII = 33000 кг, mIII = 36000 кг и mIV = 40000 кг; величина слабины каната l принята одинаковой для всех грузов. В качестве результатов моделирования получены величины токов статора электродвигателя подъема при отрыве от поверхности грузов (рис.3).
Анализируя полученные результаты можно отметить, что в рассматриваемой системе до момента времени t = 4,8 с происходит выбор слабины каната, вследствие чего ток статора одинаков для всех грузов, и его амплитуда в течение всего этапа не меняется.
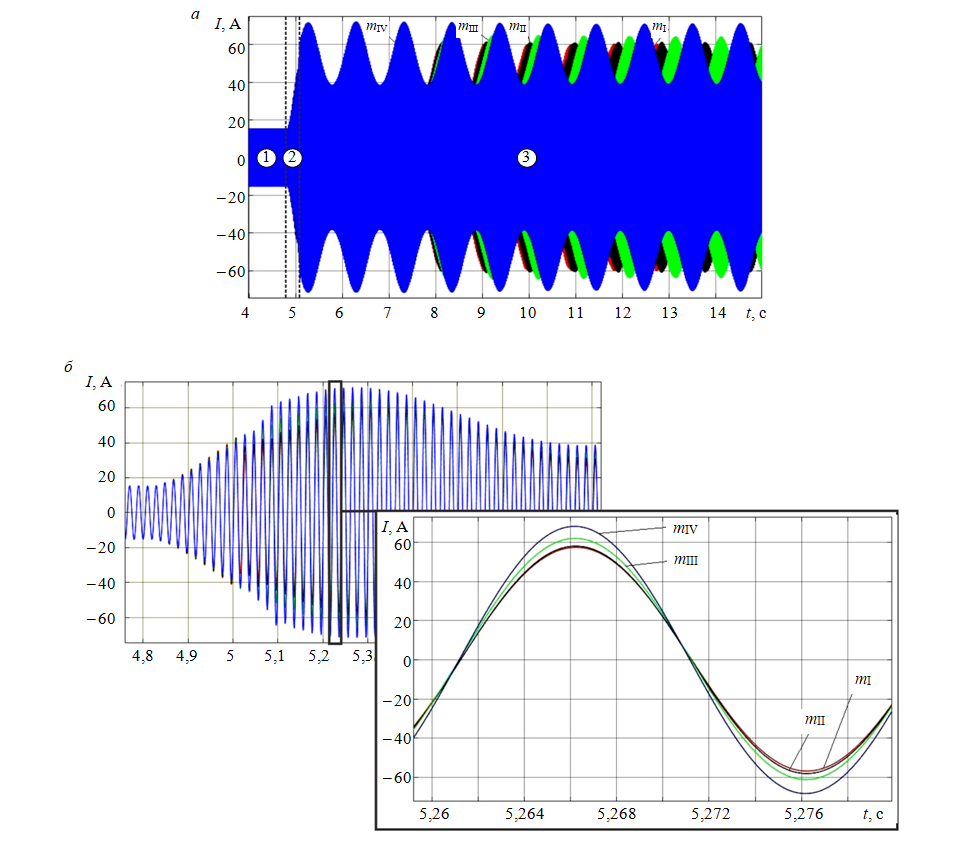
После того как первый этап подъема груза заканчивается, в канате возникает усилие, а значение тока возрастает с ростом натяжения каната механизма подъема. Условием окончания второго этапа является равенство усилия в канате веса груза, вследствие чего время окончания второго этапа для каждого из грузов различно, а разделение на рис.3, а показано условно. Для грузов большей массы длительность второго этапа увеличивается.
На третьем этапе подъема груза амплитудные значения тока колеблются с частотой, определяемой соотношением приведенных масс и жесткостью связей. Кроме изменения времени начала этапа отрыва груза, отличаются и амплитудные значения тока для разных масс, а также наблюдается смещение колебаний по фазе для грузов различной массы.
Результаты моделирования показывают, что уже за первые пять периодов сетевого напряжения после отрыва груза от опорной поверхности обнаруживается поддающаяся фиксации разница амплитуды тока статора (рис.3, б), которая для mII составила 1,8 %, для mIII – 12,7 %, а для mIV – 23,6 %. Появление различий в величинах амплитуды тока статора свидетельствует о чувствительности модели к вариации массы поднимаемого груза и подтверждает возможность диагностирования перегрузки за единицы периодов сетевого напряжения.
Моделирование процессов подъема грузов различной массы, аналогичное показанному выше, было проделано для ряда кранов различной грузоподъемности, применяемых на металлургических предприятиях. В качестве основы рассматривался парк оборудования предприятия АО «ЕВРАЗ ЗСМК» (Новокузнецк), насчитывающий 354 единицы мостовых кранов. В результате его анализа в рассматриваемый ряд мостовых кранов вошла 51 единица типоразмеров с мощностью привода 5-160 кВт и массой поднимаемого груза 5-200 т.
С использованием систем уравнений (2)-(9) и модели, показанной на рис.2, были определены величины токов статора асинхронных двигателей механизмов подъема для всех мостовых кранов рассматриваемого ряда. Для каждого из типоразмеров было выполнено моделирование ситуации перегрузки механизма подъема массой груза, превышающей номинальную на 1 %. Определялись значения фазного тока статора в первом полупериоде напряжения питающей сети при отрыве груза, и во всех случаях фиксировалось увеличение его амплитуды относительно опыта подъема с грузом номинальной массы со средневзвешенным по ряду значением отклонения 0,579 %. Для полученных результатов моделирования были исследованы статистические зависимости между мощностью привода N, грузоподъемностью крана W, увеличением амплитуды тока I и получены уравнения регрессии с коэффициентом линейной корреляции 0,75:
Дополнительные исследования показали, что увеличение амплитуды тока статора с первого по пятый период сетевого напряжения носит линейный характер, как и увеличение амплитуды тока статора при повышении массы от 1 до 10 %.
Таким образом, уравнения регрессии (10) позволяют прогнозировать увеличение амплитуды тока статора при превышении массы груза для мостовых кранов, не вошедших в рассмотренный перечень типоразмеров, и, следовательно, выступают основой для алгоритма раннего диагностирования превышения массы груза для любого мостового крана металлургических предприятий и могут быть в дальнейшем применены для определения уставки срабатывания программно-аппаратного средства защиты.
Заключение. Результаты всех вычислительных экспериментов подтвердили следующее:
• на этапе выбора слабины каната величина тока статора электродвигателя механизма подъема не зависит от массы груза;
• время до начала третьего этапа с ростом массы груза увеличивается;
• амплитудные значения тока на этапе отрыва груза возрастают с увеличением массы груза, а поддающаяся фиксации разница появляется уже после пяти периодов сетевого напряжения с начала этапа;
• частота колебаний тока после отрыва груза зависит от его массы, но изменяется в небольших пределах.
Объем полученных результатов позволил определить статистические зависимости между величинами мощности привода подъема, грузоподъемности мостового крана и отклонениями амплитуды тока электродвигателя, которые являются основой для алгоритма раннего диагностирования превышения массы груза. Таким образом, контроль тока электродвигателя подъема позволяет создать защиту грузоподъемного механизма от превышения массы груза, не требующую внесения изменений в конструктивные элементы мостовых кранов. Быстродействие предлагаемого подхода существенно выше, чем у существующих механических способов контроля перегрузки.
Литература