Прогнозирование проницаемости нефтяных пластов на основе моделирования синтетических гидродинамических исследований скважин с помощью машинного обучения
- 1 — аспирант Пермский национальный исследовательский политехнический университет ▪ Orcid ▪ Elibrary ▪ Scopus
- 2 — д-р техн. наук профессор Пермский национальный исследовательский политехнический университет ▪ Orcid ▪ Elibrary ▪ Scopus ▪ ResearcherID
Аннотация
Представлен инновационный подход к моделированию виртуальных гидродинамических исследований добывающих скважин, эксплуатирующих терригенные коллекторы нефтяных месторождений Пермского края. Для решения поставленной задачи использовались современные технологии машинного обучения (CatBoost, Random Forest, XGBoost, MLP, Gradient Boosting и др.), что позволило достичь высокой точности прогнозов. Основной параметр для моделирования и исследования – забойное давление на различных этапах его восстановления в процессе проведения гидродинамических исследований скважин. Использование метода интерпретации модели SHAP впервые позволило оценить влияние геолого-технологических параметров на величину забойного давления и выделить среди них ключевые. Анализ чувствительности модели прогнозирования восстановления забойного давления к изменению исходных параметров позволил оценить степень их влияния на формирование кривых восстановления давления (КВД). Уникальность предложенного подхода заключается в изучении значимости параметров на различных временных этапах восстановления забойного давления в процессе гидродинамического исследования, позволяющего более детально понимать процессы, происходящие в пластовых условиях. Предложенные алгоритмы позволили создать синтетические КВД, максимально приближенные к фактическим данным, а также в режиме реального времени изучать динамику проницаемости удаленной зоны пласта. Подход открывает новые горизонты в моделировании виртуальных гидродинамических исследований и позволяет с высокой степенью детализации и оперативности оценивать фильтрационные свойства пласта по всему добывающему фонду скважин одновременно. Технологическое решение направлено на оперативность оценки фильтрационных параметров удаленных зон пласта и обеспечивает возможность мониторинга изменения проницаемости, что способствует своевременному выявлению зон ухудшения притока нефти и разработке мер по восстановлению продуктивности скважин. Данный подход существенно снижает экономические риски, связанные с проведением дорогостоящих полевых испытаний, обеспечивая надежность и достоверность прогнозируемых показателей при минимальных затратах ресурсов и времени.
Финансирование
Исследования выполнены при поддержке Министерства науки и высшего образования Российской Федерации (проект № FSNM-2024-0005).
Введение
Проницаемость пластов и состояние призабойной зоны (ПЗП) – ключевые факторы, определяющие эффективность добычи нефти и газа [1, 2]. Прогнозирование и мониторинг этих параметров позволяют оптимизировать процесс разработки месторождений [3], предотвращать осложнения в ходе эксплуатации и повышать общий коэффициент извлечения углеводородов [4, 5].
Существующие методы определения проницаемости имеют множество недостатков. Эмпирические корреляции зависят от статистических связей между измерениями проницаемости керна и петрофизическими свойствами, что делает их непригодными для применения в различных геологических условиях [6, 7]. Метод индикатора зоны потока (Flow Zone Indicator, FZI) требует обширного анализа кернового материала, что обеспечивает длительный процесс, а полученные результаты могут не в полной мере отражать свойства удаленной зоны резервуара [8, 9]. Традиционные методы, основанные на эмпирических корреляциях для оценки проницаемости с использованием петрофизических данных, часто приводят к неточностям, неопределенностям и могут быть затратными по времени и дорогими [10, 11]. Прогнозирование проницаемости с использованием интерпретации данных каротажных исследований методами машинного обучения активно изучается, характеризуют свойства пласта в непосредственной близости к стволу скважины [12-14]. Перспективно прогнозирование проницаемости с анализом изображений и информации о поровом пространстве с применением методов машинного обучения, данный подход требует наличия образцов керна и не позволяет оценивать свойства в удаленных зонах пласта [15].
Одним из основных способов оценки фильтрационных параметров пласта является интерпретация гидродинамических исследований скважин (ГДИС) на неустановившихся режимах фильтрации методами восстановления давления и уровня (КВД и КВУ), особенностями которых являются продолжительная остановка скважин и сопутствующее снижение добычи нефти [16]. Достоверное прогнозирование проницаемости удаленной зоны пласта осложнено особенностями процесса интерпретации ГДИС. Необходимо выделить причины низкой кондиционности значительного количества ГДИС на территории Пермского края:
- проблема выделения участка плоскорадиальной фильтрации в связи с влиянием ствола скважины;
- недостаточная длительность исследования [17];
- влияние границы постоянного давления;
- интерференция скважин;
- низкая разрешающая способность телеметрической системы (ТМС).
В связи с ростом применения глубинных датчиков давления [18] появилась возможность широко использовать метод стабилизации давления (КСД) [19]. Однако не все скважины оснащены ТМС, что осложняет мониторинг достоверной динамики забойного давления. Наблюдаются случаи скачкообразного изменения и длительных перерывов записи давлений. Другой популярный метод – анализ кривой падения (анализ истории добычи, АД). Метод является эмпирическим и используется для оценки добычи углеводородов, для фильтрационных параметров пласта и его состояния (скин-фактор). Данной технологии сопутствует ряд недостатков: необходимость стабильной работы соседних скважин, неопределенность режимов фильтрации в условиях многослойных залежей и коллекторов с несколькими типами пустотных пространств, флуктуация ключевых параметров [20, 21]. Преимуществом методов КСД и АД является отсутствие необходимости остановки скважин, однако увеличение длительности исследований влечет к неопределенности появления косвенных факторов и ограничений [22].
Активно изучаются и совершенствуются методы машинного обучения для оценки проницаемости коллекторов. Использование в исследованиях [23-25] искусственной нейронной сети (ИНС) для прогнозирования проницаемости показало более высокие метрики в сравнении с множественной линейной регрессией (Multiple Linear Regression, MLR) и нелинейной регрессией (Multiple Nonlinear Regression, MNLR). Авторы работы [26] предложили эволюционирующую ИНС с оптимизатором на основе генетического алгоритма (Genetic Algorithm, GA), добившись более высокой точности, чем у стандартной ИНС. В исследовании [27] использовалась комбинация MLP (Multilayer Perception), RBF (Radial Basis Function) и GRNN (Generalized Regression Neural Network) сетей, оптимизированных с помощью GA, что обеспечило повышение точности предсказаний. Авторы работы [28] исследовали алгоритмы PSO (Particle Swarm Optimization) и SSD (Social Ski-Driver) для предсказания проницаемости, выяснив, что наивысшую точность демонстрирует модель MLP-SSD после выбора признаков с использованием библиотеки SHAP (Shapley Additive Explanations). Данная библиотека также применена в исследованиях [29, 30] для выбора и интерпретации признаков, при этом модель PSO-XGBoost показала наилучшие результаты.
Несмотря на перспективность ИНС, существует проблема медленной сходимости – скорость обучения определяет, насколько быстро модель адаптируется к задаче. Высокая скорость обучения может привести к неоптимальному решению, низкая – к замедлению процесса сходимости, т.е. изменения весов модели в целях снижения ошибки. В работе [31] представлено решение данной проблемы с помощью модели модульной нейронной сети (Modular Neural Network, MNN). Использование нейронной сети RBF [32] обеспечило повышение скорости прогнозирования проницаемости по пористости в сравнении со стандартной полносвязной. В работе [33] объединены ИНС и нечеткая логика, комбинация преимуществ которых обеспечила повышение точности прогнозирования проницаемости в сравнении с результатами применения моделей по отдельности. В исследовании [34] использован ядерный магнитный резонанс (Nuclear Magnetic Resonance, NMR) в сочетании с каротажными данными для улучшения метрик прогнозирования проницаемости. Применение функциональной сети (FN) [35] обеспечило лучшие результаты в сравнении с ИНС и методами регрессии. Учеными [36] использована регрессия с вектором релевантности (Relevance Vector Regression, RVR) и оптимизацией GA, которая превзошла результаты модели SVM (Support Vector Machine). В работе [37] применена нечеткая логика для эффективного прогнозирования проницаемости. Предложенная техника кластеризации подтвердила свою эффективность и точность. Автор исследования [7] улучшил нечеткую логику с помощью инженерии признаков для более точных прогнозов проницаемости. Это позволило повысить коэффициент детерминации R2 до 0,76 в сравнении с линейной регрессией (0,04) и применением нечеткой логики без инженерии признаков (0,41). В исследовании [38] сравнены модели MLP, SVR (Support Vector Regression) и MLR, MLP и SVR продемонстрировали высокую точность. В работе [39] авторы использовали модели LSSVM и MELM (Multilayer Extreme Learning Machine), оптимизированные с помощью COA (Cuckoo Optimization Algorithm), PSO и GA, для прогнозирования проницаемости, при этом гибрид MELM-COA показал более высокие метрики (Root Mean Square Error, RMSE – 0,56), чем LSSVM и MELM с оптимизаторами PSO, GA, а также CNN (Convolutional Neural Network) (RMSE от 0,72 до 1,24).
В работе [40] предложена ансамблевая модель машинного обучения, которая показала более высокие результаты в сравнении с одинарными конфигурациями. Метод бэггинга [15] для прогнозирования проницаемости показал наилучшие метрики. Применение ансамблей моделей также представлено в ряде других исследований [41-43]. Авторами работы [44] использована эмпирическая формула и новая ансамблевая модель для более точного прогнозирования проницаемости. Объединение моделей SVM, ИНС и ANFIS (Adaptive Neuro-Fuzzy Inference System) повысило точность прогнозирования проницаемости в гетерогенных нефтяных месторождениях [45]. В работе [46] предложен гибрид SVM-T2FL (Fuzzy Logic) с FN и выбором признаков, который продемонстрировал отличные результаты моделей прогнозирования проницаемости. Авторы [47] предложили уникальную модель MIRes (Multiple-Input deep Residual) CNN для прогнозирования проницаемости, использующую комплексирование цифровых и графических данных, что превзошло SIRes 1D-CNN, SIRes 2D-CNN (Single-Input deep Residual one (two) Dimensional CNN), GMDH (Group Method of Data Handling). Разработана гибридная модель с использованием Random Forest, Lasso Regularization и XGBoost [43] для прогнозирования проницаемости.
Анализ научно-технической литературы показывает, что научным сообществом активно развиваются методы машинного обучения (МО) для оценки и прогнозирования проницаемости. Тем не менее, большинство применяемых на текущее время технологий МО опираются на данные каротажа [48]. Недостатками данного подхода являются невозможность оценки средней эффективной проницаемости зоны дренирования скважины и необходимость актуальных геофизических исследований, на основе которых выполняется оценка.
В настоящем исследовании впервые используются значительные базы данных (Big Data) по гидродинамическим исследованиям скважин (кривые восстановления давления, эксплуатационные параметры до остановки скважин на исследования, геолого-физические свойства пласта и нефти), проведенные за всю историю эксплуатации терригенных отложений нефтяных месторождений Пермского края. Уникальность работы заключается в разработке подхода для прогнозирования забойного давления в момент восстановления, что в будущем исключает особенности и погрешности процесса интерпретации. Представленный алгоритм позволяет моделировать кривую восстановления давления в скважине в реальном времени, что значительно ускоряет определение фильтрационных параметров и позволяет охватить весь фонд скважин. Предлагаемый подход способствует более эффективной и экономически рациональной разработке месторождений, обеспечивая оптимизацию ресурсов и улучшение процесса принятия решений в нефтедобыче. Мы, конечно, не говорим о полном исключении гидродинамических исследований, так как они предназначены для выполнения своих функций, в том числе для уточнения моделей. Синтетические исследования необходимы для описания процессов, происходящих в пласте, прогноза технологических и экономических показателей.
Методы
Сформирована база высокоинформативных гидродинамических исследований терригенных коллекторов месторождений Пермского края. Из выборки исключались ГДИС с выраженным влиянием соседних скважин, низкой разрешающей способностью ТМС, некондиционными замерами восстановления забойного давления. Доля гидродинамических исследований с указанными особенностями составляет около 15 %. Таким образом, первичная исходная информация для обучения состоит из 85 % всех анализируемых ГДИС (≈3500), в том числе содержит эксплуатационные параметры скважин, время восстановления давления, геолого-физические свойства пласта и нефти. В качестве категориального признака использовались профиль скважин (наклонно-направленная (ННС), горизонтальная (ГС) и технология их освоения (гидравлический разрыв пласта (ГРП), многостадийный гидравлический разрыв пласта (МГРП). Диапазоны изменения исходных параметров: забойное давление – 0,5-24 МПа; обводненность – 0-99,9 %; дебит жидкости – 0,1-244,8 м3/сут; объемный коэффициент нефти – 1,0-1,7; коэффициент сжимаемости пласта – 1,1-4,6 (МПа·104)–1; коэффициент сжимаемости породы – 0,7-1,5 (МПа·104)–1; газосодержание – 1,2-1210 м3/т; коэффициент сжимаемости нефти – 2,5-26,2 (МПа·104)–1; плотность нефти – 0,6-1,2 г/см3; эффективная нефтенасыщенная толщина – 0,4-19,6 м; вязкость нефти – 0,5-114,1 мПа·с; пластовое давление –1,9-24,9 МПа; пористость – 4,6-34 %; давление насыщения – 3,9-22,9 МПа; забойное давление в момент восстановления – 0,1-23,3 МПа; время восстановления – 0-265047 мин. Для работы с категориальным признаком, содержащим четыре уникальных значения, применен метод OHE (One-Hot Encoding). Он преобразует категориальный признак в несколько бинарных столбцов, каждый из которых соответствует одному из уникальных значений исходного признака. Рекомендуемая модель CatBoost автоматически обрабатывает категориальные признаки без необходимости их предварительного кодирования. Прогнозируемым параметром является забойное давление в каждый временной период восстановления КВД. Путем последовательного прогнозирования восстановления забойного давления на различных интервалах длительности исследования обеспечивается моделирование синтетической кривой восстановления давления.
Для оценки пластового давления используются результаты вычислений в модульном сервисе Data Stream Analytics [49]. Данный сервис определяет пластовое давление на основе геолого-промысловой информации с помощью методов машинного обучения как на ретроспективный, так и на перспективный один год периоды. Появляется возможность моделирования синтетических кривых восстановления давления на любой момент в ретроспективе и в прогнозе без остановки скважин на время исследования.
В качестве моделей прогнозирования использовались техники машинного обучения:
- MLP Neural Network (многослойный перцептрон) – тип искусственной нейронной сети, состоящий из нескольких слоев нейронов (входного, скрытых и выходного), которые позволяют моделировать сложные нелинейные зависимости.
- Gradient Boosting – метод ансамблирования, который создает последовательность моделей, каждая из которых исправляет ошибки предыдущих. Обычно используется с деревьями решений и отличается высокой точностью.
- Random Forest – ансамблевый алгоритм, который строит множество деревьев решений на случайных подмножествах данных и признаков. Его предсказания усредняются (для регрессии) или определяются голосованием (для классификации). Обеспечивает устойчивость к переобучению и хорошо работает с различными типами данных.
- XGBoost – это оптимизированная версия градиентного бустинга, разработанная для высокой производительности и точности. Она включает регуляризацию, параллельное обучение и другие улучшения.
- Decision Tree – интерпретируемый и простой алгоритм, который строит древовидную модель для принятия решений. Разветвления основаны на правилах, минимизирующих ошибки. Однако алгоритм склонен к переобучению без ограничения глубины.
- Linear Regression – классический статистический метод, который предполагает линейную зависимость между входными признаками и целевой переменной. Отличается простотой, интерпретируемостью и скоростью, но ограничен в моделировании сложных нелинейных зависимостей.
- SVR – алгоритм, который строит гиперплоскость, максимально точно описывающую зависимость между признаками и целевой переменной, минимизируя ошибки в пределах заданной погрешности. Подходит для небольших выборок, но требователен к вычислительным ресурсам.
- K-Nearest Neighbors – метод, основанный на поиске ближайших соседей объекта. Предсказание основывается на значениях целевой переменной у k самых близких объектов. Прост и эффективен, но чувствителен к размеру данных и шуму в выборке.
- CatBoost – алгоритм градиентного бустинга, предотвращает переобучение и обеспечивает высокую производительность и точность. Гиперпараметры подбирались с помощью фреймворка Optuna. Optuna – это библиотека для поиска гиперпараметров в машинном обучении. Она предоставляет удобный интерфейс для проведения оптимизации гиперпараметров с использованием различных алгоритмов поиска. Варьировались следующие параметры: скорость обучения (learning_rate) – 0,01-0,3; коэффициент L2-регуляризации (l2_leaf_reg) – 1e-8-100,0; температура бэггинга (bagging_temperature) – 0,0-10,0; интенсивность случайного шума (random_strength) – 1e-8-10,0; глубина дерева (depth) – 4-10; количество границ для разбиения признаков (border_count) – 32-255; минимальное количество объектов в листе (min_data_in_leaf) – 1-100; стратегия роста дерева (grow_policy) – SymmetricTree, Depthwise, Lossguide. В процессе оптимизации использовалась кросс-валидация для оценки точности модели на различных подмножествах обучающих данных. Наилучшие гиперпараметры: 'depth' – 10; 'learning_rate' – 0,128; 'l2_leaf_reg' – 0,0117; 'bagging_temperature' – 6,509; 'random_strength' – 1,501; 'border_count' – 183; 'min_data_in_leaf' – 5; 'grow_policy' – 'Depthwise'.
Формирование обучающего цифрового массива осуществлялось следующим образом:
- Выполнялись верификация и последовательный выбор кривых восстановления давления. Проверялось отсутствие выбросов, резких скачков и ступенчатого изменения восстановления забойного давления.
- Последовательно для каждой КВД в таблицу заносились данные длительности восстановления и значения забойного давления. Формировались два столбца: длительность восстановления и забойное давление (для каждой точки КВД). Строки представляют собой результаты замеров КВД, каждая точка графика является строкой таблицы.
- Для каждой точки выбранной кривой восстановления давления добавлялись константы параметров в качестве новых столбцов, соответствующих значениям до остановки скважины: дебит жидкости, обводненность, пластовое давление, забойное давление, проницаемость ПЗП, время восстановления (время после остановки скважины), пористость, коэффициент сжимаемости породы, коэффициент сжимаемости пласта, эффективная нефтенасыщенная толщина пласта, вязкость нефти, газосодержание, плотность нефти, коэффициент сжимаемости нефти, объемный коэффициент нефти, давление насыщения. При обучении моделей использованы значения пластового давления, полученные при интерпретации кондиционных гидродинамических исследований скважин и в модульном сервисе Data Stream Analytics.
Для установления связей между признаками построена корреляционная матрица по Спирмену (рис.1). Корреляция по Спирмену измеряет связь между переменными на основе рангов, а не фактических значений. Она используется для определения связи между переменными, особенно когда данные не являются нормально распределенными или когда связь нелинейная. Анализ тепловой матрицы показывает, что параметры забойного, пластового давлений и дебита скважины обладают наибольшей корреляционной связью с закономерностью восстановления давления в скважине. Необходимо также отметить высокую связь исходных параметров: прямую зависимость объемного коэффициента от газосодержания и сжимаемости нефти и обратную – от плотности и вязкости нефти; сжимаемости породы от пористости; вязкости нефти от плотности нефти. Мы осознаем потенциальную проблему мультиколлинеарности, наблюдаемую на рис.1. Поскольку цель заключалась в получении общего представления о влиянии выбранных параметров, возможные искажения вследствие мультиколлинеарности признаны допустимыми в рамках данного исследования. Для повышения надежности полученных результатов планируется более детальное исследование способов снижения влияния мультиколлинеарности отбором наиболее значимых признаков, нормализацией данных и применением регуляризации.
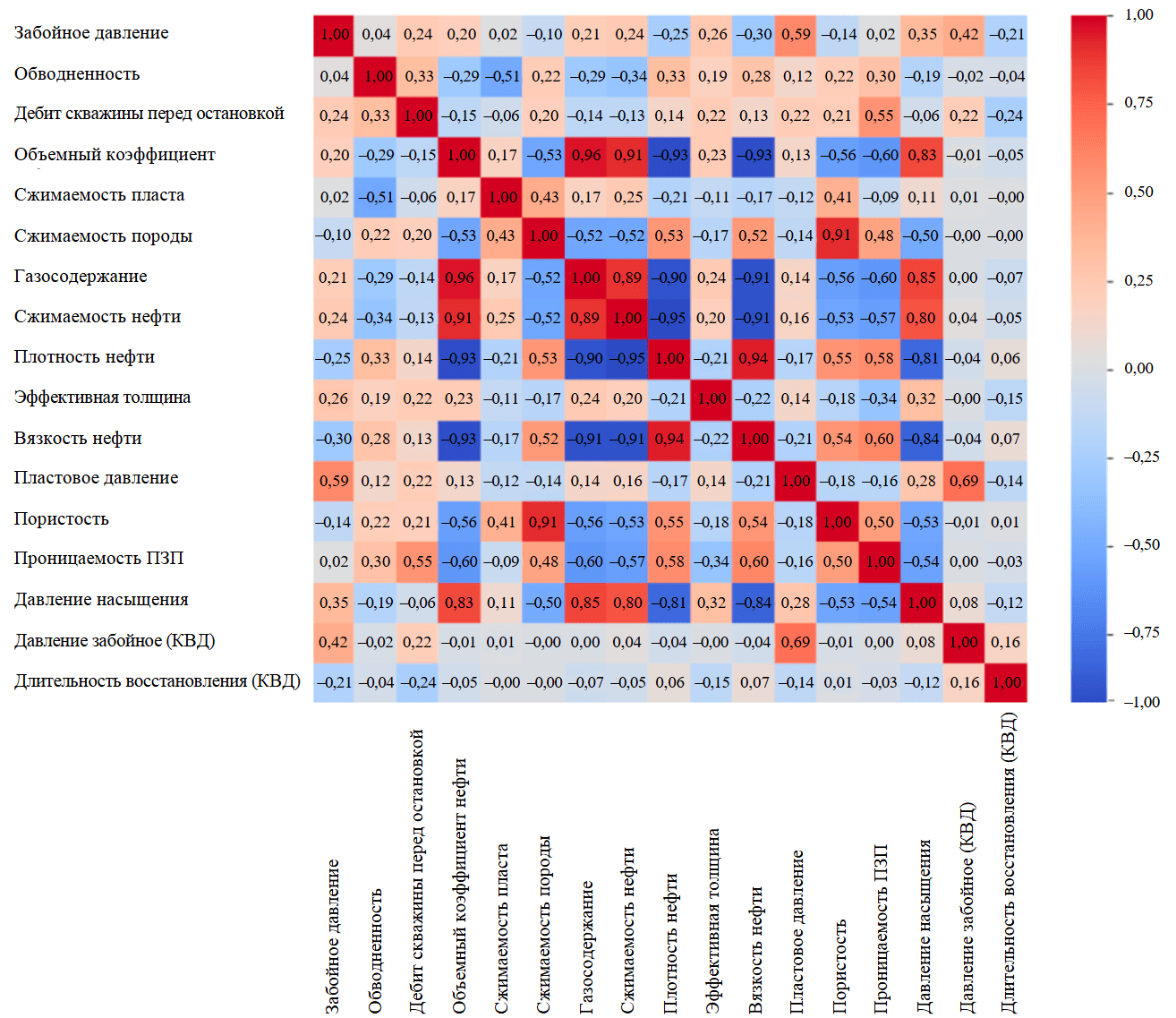
Рис.1. Корреляционная матрица исходных данных по Спирмену
Представленный алгоритм применялся для каждой КВД, последовательно формируя цифровой массив. Прогнозируемым параметром является забойное давление в момент восстановления. Цифровой массив разделен на обучающую, валидационную и тестовую выборки в соотношении 80, 10 и 10 %. Для выравнивания вклада признаков использовано масштабирование MinMaxScaler, которое нормализует данные от 0 до 1.
Для отладки и оценки моделей использованы статистические метрики – коэффициент детерминации R2 и корень среднеквадратичного отклонения RMSE
где yi – фактическое значение; yˆi – предсказанное значение; n – количество наблюдений; y¯i – среднее значение фактических данных.
Алгоритм технологии выстроен следующим образом:
- Сбор данных гидродинамических исследований всего фонда скважин за ретроспективный период, включающих исходные параметры (свойства пласта, нефти и эксплуатационные параметры), динамику восстановления забойного давления и данные интерпретации (пластовое давление).
- Подготовка, очистка и обработка данных.
- Обучение моделей воспринятию закономерности восстановления забойного давления в зависимости от входных параметров.
- Получение прогнозной синтетической кривой восстановления давления на текущий период на основе предобученной модели на ретроспективных гидродинамических исследованиях, проведенных на скважинах, и актуальной геолого-промысловой информации.
- Интерпретация синтетической кривой восстановления давления и получение прогнозной величины проницаемости удаленной зоны пласта.
Результаты и обсуждение
Выполнено обучение и сравнение метрик R2 и RMSE, представленное в таблице, как индивидуальных моделей машинного обучения для прогнозирования забойного давления в момент восстановления, так и ансамбля наилучших для валидационной выборки. Анализ сходимости прогнозных и фактических значений выбранных моделей показывает, что наилучший результат получен с помощью CatBoost – библиотеки градиентного бустинга с открытым исходным кодом на основе деревьев решений.
Метрики качества моделей машинного обучения
|
Модель |
R2 |
RMSE |
|
CatBoost |
0,997 |
0,176 |
|
Random Forest |
0,995 |
0,273 |
|
XGBoost |
0,988 |
0,406 |
|
Decision Tree |
0,987 |
0,432 |
|
MLP Neural Network |
0,983 |
0,498 |
|
Ensemble |
0,970 |
0,670 |
|
Gradient Boosting |
0,878 |
1,354 |
|
Linear Regression |
0,709 |
2,089 |
|
K-Nearest Neighbors |
0,331 |
3,171 |
|
SVR |
0,139 |
3,596 |
На рис.2, а приведено корреляционное поле прогнозных и фактических значений забойного давления в моменты восстановления. Коэффициент линейной корреляции прогнозных и фактических значений r для тестовой выборки составил 0,97, RMSE – ~0,18. Синтетическая кривая восстановления давления, представленная на рис.2, б, близка к фактической, это показывает, что модели машинного обучения обладают способностью к обучению для решения поставленной задачи. Можно сделать вывод о перспективности применения данных алгоритмов для оценки проницаемости удаленной зоны пласта путем интерпретации синтетической КВД.
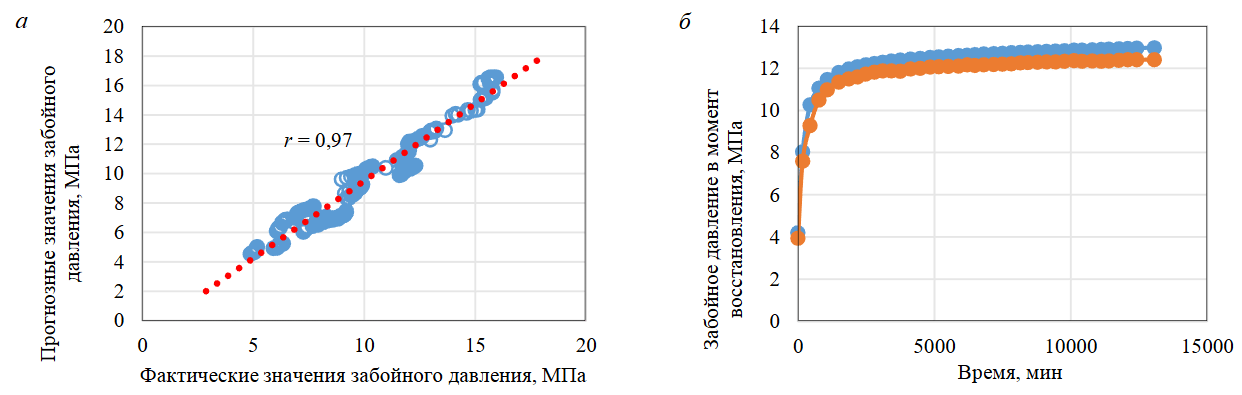
Рис.2. Диаграмма рассеяния прогнозных и фактических значений давления в момент восстановления (а); пример прогнозирования кривой восстановления давления (б)
Для комплексного исследования значимости исходных параметров применен градиентный бустинг – техника машинного обучения для задач классификации и регрессии, которая строит модель предсказания в форме ансамбля слабых предсказывающих моделей, обычно деревьев решений. Задача решалась с использованием библиотеки SHAP и выявлением вклада каждого признака в конечное предсказание искомой величины – забойного давления в момент восстановления. SHAP – это метод на основе вектора Шепли, позволяющий выявить значимость (мера влияния параметра на результат предсказания) каждого признака. Для определения значимости параметра происходит оценка предсказаний модели с данным признаком и без него.
Значимости признаков для прогнозирования восстановления давления для выборки: пластовое давление, МПа – 0,309; забойное давление, МПа – 0,209; время восстановления, мин – 0,193; дебит жидкости, м3/сут – 0,053; обводненность, % – 0,039; проницаемость ПЗП, мкм2 – 0,024; профиль скважины и технология освоения – 0,024; газосодержание, м3/т – 0,024; эффективная нефтенасыщенная толщина, м – 0,024; давление насыщения, МПа – 0,022; коэффициент сжимаемости пласта, (МПа·104)–1 – 0,016; пористость, % – 0,013; вязкость нефти, мПа·с – 0,013; коэффициент сжимаемости нефти, (МПа·104)–1 – 0,011; коэффициент сжимаемости породы, (МПа·104)–1 – 0,011; плотность нефти, г/см3 – 0,008; объемный коэффициент нефти – 0,007. Закономерно наибольшее влияние пластового и забойного давлений и времени восстановления. Тем не менее, важной особенностью является влияние других признаков на формирование восстановления давления в скважине.
Данный подход использован на различных значениях длительности исследования для изучения природы процесса восстановления давления в скважине. Параметр времени ранжировался от минимального до максимального значений и разбивался на 10 участков, чтобы в полной мере отразить распределение величин и обеспечить выявление потенциальных закономерностей. По каждому интервалу формировался цифровой массив, по которому с помощью библиотеки SHAP оценивалась значимость параметров для восстановления давления в скважине. На рис.3, а представлены лепестковые диаграммы значимости исходных параметров для различных значений длительности восстановления. Анализ показывает, что на начальном этапе восстановления давления выделяется параметр сжимаемости пласта. Дебит жидкости оказывает влияние на всех этапах восстановления, но наблюдается смещение на поздние этапы временных интервалов. Значимость параметра газосодержания преобладает на начальных этапах восстановления давления в скважине. Значимость вязкости нефти нарастает на высоких значениях времени восстановления. Значимость эффективной нефтенасыщенной толщины прослеживается на всех интервалах длительности КВД. Прослеживается рост значимости обводненности и сжимаемости породы на высоких значениях длительности восстановления.
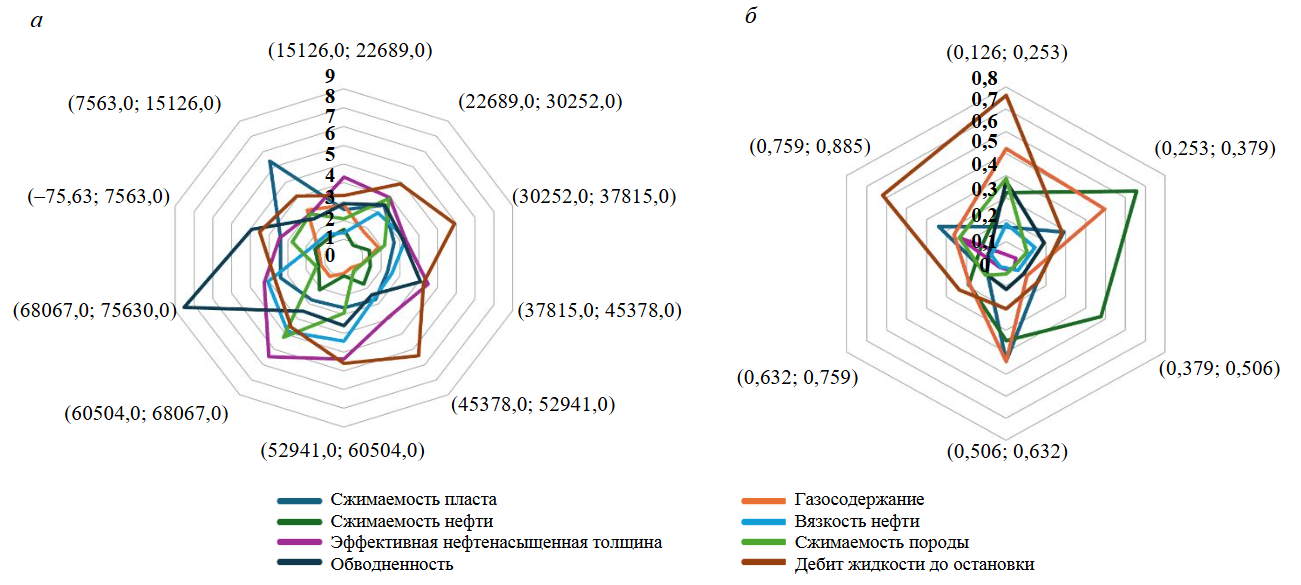
Рис.3. Значимость параметров на восстановление давления в скважине на различных диапазонах времени (а) и на различных участках восстановления (б)
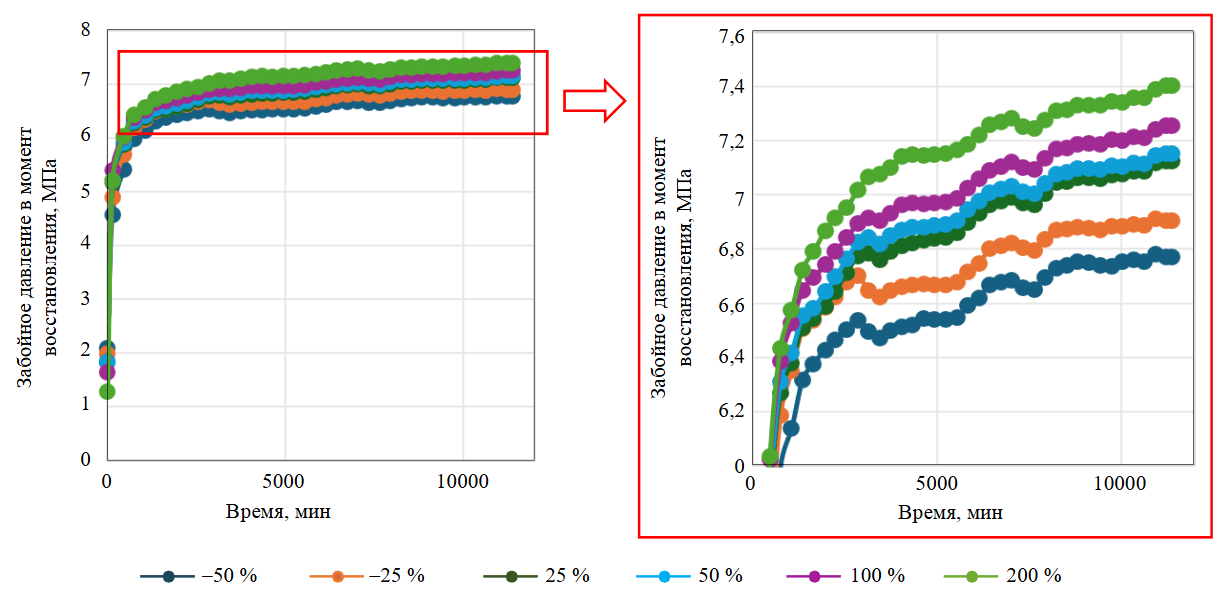
Рис.4. Анализ чувствительности синтетической кривой восстановления давления на изменение дебита жидкости
Аналогичным образом анализ проведен на различных этапах восстановления КВД. Для этого введена дополнительная переменная, представляющая собой отношение забойного давления в определенный интервал восстановления к пластовому давлению. На рис.3, б представлены лепестковые диаграммы значимости исходных параметров для различных участков восстановления. Анализ показывает, что на начальном этапе восстановления давления выделяется параметр сжимаемости пласта. Дебит жидкости оказывает влияние преимущественно на начальный и конечный периоды КВД. Значимость параметра газосодержания преобладает на начальном этапе восстановления давления в скважине. На конечном этапе КВД значимым является параметр эффективной нефтенасыщенной толщины.
Следующим этапом анализа является оценка чувствительности кривой восстановления давления на изменение исходных параметров. Каждый исходный параметр варьировался последовательно от –50 до +200 % без изменения остальных, и на основе этих данных строятся фактическая и прогнозная кривые восстановления давления. Установлено, что модель обучается и чувствительна к изменению каждого из анализируемых параметров. Наиболее важным признаком является дебит скважины, и на рис.4 представлен анализ чувствительности восстановления забойного давления от данного параметра. На рис.4 видно, что модель обучаема и динамика восстановления давления реагирует на изменение дебита жидкости.
На следующем этапе выполнено сравнение результатов интерпретации фактических (не задействованных в обучении) и синтетических кривых восстановления давления, представленное на рис.5 и показавшее высокую сходимость результатов (r составляет 0,95). Данный подход перспективен для прогнозирования фильтрационных параметров удаленной зоны пласта и исключает неопределенности, связанные с особенностями интерпретации ГДИС.
На рис.6 представлено прогнозирование пластового давления в модульном сервисе Data Stream Analytics на ретроспективный (красная линия) и перспективный (один год, фиолетовая линия) периоды. Таким образом, возможно моделирование синтетических кривых восстановления давления на прогнозный момент времени для оценки проницаемости удаленной зоны дренирования скважин при изменении энергетического состояния залежи.
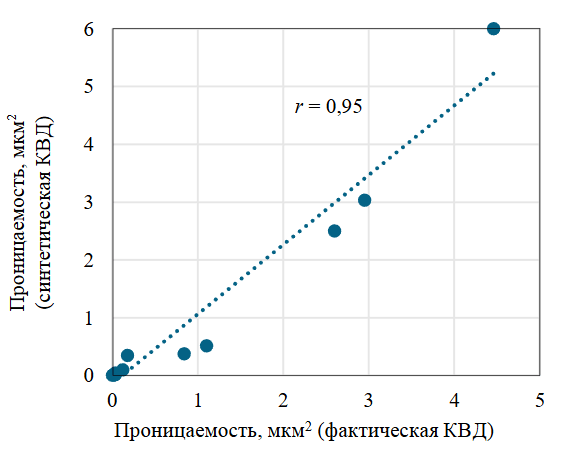
Рис.5. Сравнение результатов интерпретации фактических и синтетических КВД
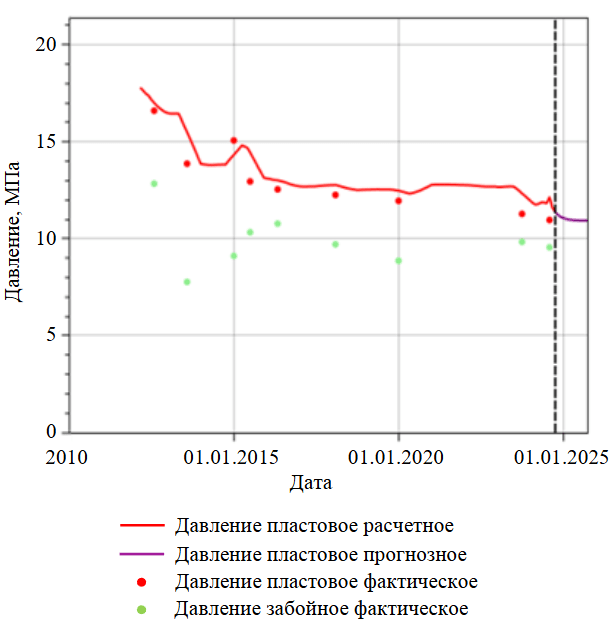
Рис.6. Прогнозирование пластового давления в модульном сервисе Data Stream Analytics
На рис.7 показаны фактическая КВД (на 01.08.2024 – зеленая линия), синтетические КВД на текущее состояние (01.12.2024 – голубая линия) и перспективный период (01.10.2025 – красная линия) и результаты их интерпретации. Применение данных алгоритмов может позволить осуществлять мониторинг фильтрационных параметров в реальном времени и оценивать влияние пластового давления на проницаемость пласта на перспективный период. В качестве прогнозного пластового давления на 01.10.2025 использовано значение 10,86 МПа, рассчитанное в модульном сервисе Data Stream Analytics (рис.6, фиолетовая линия).
Анализ рис.7 показывает высокую сходимость фактической (темно-зеленая линия) и синтетической (светло-зеленая линия) КВД на 01.08.2024. Результаты интерпретации фактической и синтетических кривых восстановления забойного давления характеризуют отрицательную прогнозную динамику проницаемости удаленной зоны пласта (с 0,0462 до 0,0348 мкм2), соответствующую снижению пластового давления (с 11,21 до 10,86 МПа).
Интеграция методов машинного обучения и использование кривых восстановления давления в реальном времени перспективны для контроля разработки месторождений углеводородов. Эти технологии не только увеличат достоверность определения и прогнозирования проницаемости, но и сократят время простоя, связанное с традиционными методами испытания скважин. Представленные в работе алгоритмы позволят строить динамические карты распределения проницаемости объекта разработки для выявления закономерностей фильтрации и вовлечения запасов углеводородов. В качестве направления будущих работ можно отметить расширение набора исходных параметров и генерацию производных на их основе, а также использование других алгоритмов прогнозирования КВД, в том числе гибридных моделей.
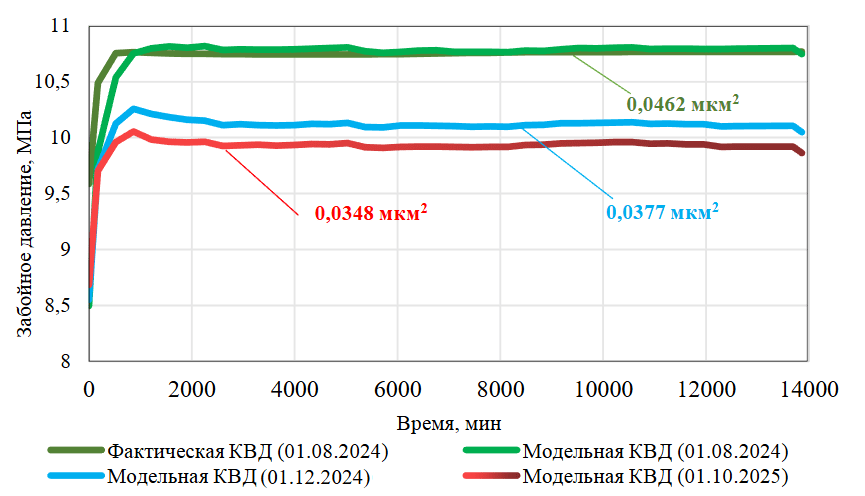
Рис.7. Моделирование синтетических КВД в период с 01.08.2024 по 01.10.2025 и результаты их интерпретации
Заключение
Проницаемость пластов и состояние призабойной зоны являются ключевыми параметрами, влияющими на эффективность разработки нефтегазовых месторождений. В данной работе предложен инновационный подход для прогнозирования восстановления забойного давления и моделирования кривой восстановления давления на основе методов машинного обучения (CatBoost).
Разработанный алгоритм на основе данных гидродинамических исследований скважин и геолого-физических параметров повышает точность оценки проницаемости. Использование библиотеки SHAP позволило выявить значимость исходных параметров на различных этапах восстановления давления. Анализ чувствительности подтвердил способность моделей учитывать изменения параметров и их влияние на КВД.
Разработанный подход обеспечил высокую сходимость прогнозных и фактических кривых восстановления давления, что делает его перспективным инструментом для контроля и оптимизации разработки месторождений. Коэффициент линейной корреляции прогнозных и фактических значений r для тестовой выборки прогнозирования забойного давления в момент восстановления составил 0,97, RMSE – ~0,18.
Высокие статистические метрики модели машинного обучения на основе накопленной геолого-промысловой информации демонстрируют возможность моделирования синтетических КВД в реальном времени и их интерпретации для оценки изменений проницаемости удаленной зоны пласта одновременно по всему фонду скважин. Коэффициент линейной корреляции прогнозных и фактических значений r при сравнении результатов интерпретации фактических и синтетических КВД составляет 0,95.
Проницаемость удаленной зоны продуктивного пласта играет ключевую роль в оценке эффективности нефтедобычи. Основным способом ее определения служат гидродинамические исследования скважин, обладающие существенными ограничениями – неполнотой охвата фонда скважин, низкой регулярностью измерений и необходимостью остановки скважин.
Предложенный в статье инновационный подход предусматривает непрерывную оценку фильтрационных характеристик по всему действующему фонду скважин в реальном времени. Разработанный метод ускоряет мониторинг состояния призабойной зоны, обеспечивая своевременное выявление кандидатов для проведения эффективных геолого-технических мероприятий. Преимуществом алгоритма является использование кондиционных замеров забойного давления в момент восстановления.
Алгоритмы основаны и проверены на значительных базах данных по гидродинамическим исследованиям скважин терригенных отложений нефтяных месторождений Пермского края. Описанный подход исключает особенности процесса интерпретации и значительно ускоряет определение фильтрационных параметров, расширяет охват, обеспечивая своевременное и точное обновление моделей, что в свою очередь, окажет влияние на повышение эффективности прогнозирования технологических и экономических показателей разработки.
Литература
- Язьков А.В., Колбиков С.В., Шадчнев Н.А. и др. Геолого-технологические вызовы и опыт разработки трудноизвлекаемых запасов // Георесурсы. 2024. T. 26. № 3. C. 7-12. DOI: 10.18599/grs.2024.3.1
- Индрупский И.М., Ибрагимов И.И., Цаган-Манджиев Т.Н. и др. Лабораторная, численная и промысловая оценка эффективности циклического геомеханического воздействия на карбонатном коллекторе турнейского яруса // Записки Горного института. 2023. Т. 262. С. 581-593. DOI: 10.31897/PMI.2023.5
- Kanin E., Garipova A., Boronin S. et al. Combined mechanistic and machine learning method for construction of oil reservoir permeability map consistent with well test measurements // Petroleum Research. 2025. Vol. 10. Iss. 2. P. 247-265. DOI: 10.1016/j.ptlrs.2024.09.001
- Byrne M.T., McPhee C.A. The Extinction of Skin // SPE International Symposium and Exhibition on Formation Damage Control, 15-17 February 2012, Lafayette, LA, USA. OnePetro, 2012. № SPE-151807-MS. DOI: 10.2118/151807-MS
- Al-Obaidi S.H., Khalaf F.H., Alwan H.H. Performance Analysis of Hydrocarbon Wells Based on the Skin Zone // Technium. 2021. Vol. 3. Iss. 4. P. 50-56.
- Belhouchet H.E., Benzagouta M.S., Dobbi A. et al. A new empirical model for enhancing well log permeability prediction, using nonlinear regression method: Case study from Hassi-Berkine oil field reservoir – Algeria // Journal of King Saud University – Engineering Sciences. 2021. Vol. 33. Iss. 2. P. 136-145. DOI: 10.1016/j.jksues.2020.04.008
- Xidong Wang, Shaochun Yang, Ya Wang et al. Improved permeability prediction based on the feature engineering of petrophysics and fuzzy logic analysis in low porosity–permeability reservoir // Journal of Petroleum Exploration and Production Tech-nology. 2019. Vol. 9. Iss. 2. P. 869-887. DOI: 10.1007/s13202-018-0556-y
- Mirzaei-Paiaman A., Asadolahpour S.R., Saboorian-Jooybari H. et al. A new framework for selection of representative samples for special core analysis // Petroleum Research. 2020. Vol. 5. Iss. 3. P. 210-226. DOI: 10.1016/j.ptlrs.2020.06.003
- Mirzaei-Paiaman A., Saboorian-Jooybari H., Pourafshary P. Improved Method to Identify Hydraulic Flow Units for Res-ervoir Characterization // Energy Technology. 2015. Vol. 3. Iss. 7. P. 726-733. DOI: 10.1002/ente.201500010
- Кочегуров А.И., Денисов В.И., Задорожных Е.А. Анализ применения методов машинного обучения в задачах клас-сификации пород на образцах керна // Известия Томского политехнического университета. Инжиниринг георесурсов. 2024. Т. 335. № 9. С. 148-159. DOI: 10.18799/24131830/2024/9/4792
- Soromotin A.V., Martyushev D.A., Pereira J.L.J. On the application of machine learning algorithms in predicting the permea-bility of oil reservoirs // Artificial Intelligence in Geosciences. 2025. Vol. 6. Iss. 2. № 100126. DOI: 10.1016/j.aiig.2025.100126
- Bennis M., Torres-Verdín C. Automatic Multiwell Assessment of Flow-Related Petrophysical Properties of Tight-Gas Sandstones Based on the Physics of Mud-Filtrate Invasion // SPE Reservoir Evaluation & Engineering. 2023. Vol. 26. Iss. 3. P. 543-564. DOI: 10.2118/214668-PA
- Ishola O., Vilcáez J. Machine learning modeling of permeability in 3D heterogeneous porous media using a novel stochastic pore-scale simulation approach // Fuel. 2022. Vol. 321. № 124044. DOI: 10.1016/j.fuel.2022.124044
- Singh M., Makarychev G., Mustapha H. et al. Machine Learning Assisted Petrophysical Logs Quality Control, Editing and Reconstruction // Abu Dhabi International Petroleum Exhibition & Conference, 9-12 November 2020, Abu Dhabi, UAE. OnePetro, 2020. № SPE-202977-MS. DOI: 10.2118/202977-MS
- Qing Kang, Kai-Qi Li, Jin-Long Fu, Yong Liu. Hybrid LBM and machine learning algorithms for permeability prediction of porous media: A comparative study // Computers and Geotechnics. 2024. Vol. 168. № 106163. DOI: 10.1016/j.compgeo.2024.106163
- Jirjees A.Y., Abdulaziz A.M. Influences of uncertainty in well log petrophysics and fluid properties on well test interpretation: An application in West Al Qurna Oil Field, South Iraq // Egyptian Journal of Petroleum. 2019. Vol. 28. Iss. 4. P. 383-392. DOI: 10.1016/j.ejpe.2019.08.005
- Мартюшев Д.А., Слушкина А.Ю. Оценка информативности определения фильтрационных параметров пласта на основе интерпретации кривых стабилизации давления // Известия Томского политехнического университета. Инжиниринг георесурсов. 2019. Т. 330. № 10. С. 26-32. DOI: 10.18799/24131830/2019/10/2295
- Kaleem W., Tewari S., Fogat M., Martyushev D.A. A hybrid machine learning approach based study of production forecasting and factors influencing the multiphase flow through surface chokes // Petroleum. 2024. Vol. 10. Iss. 2. P. 354-371. DOI: 10.1016/j.petlm.2023.06.001
- Юдин В.А., Вольпин С.Г., Ефимова Н.П., Афанаскин И.В. Особенности кривой стабилизации давления в скважине, расположенной в зоне динамического влияния разлома // Нефтепромысловое дело. 2020. № 12 (624). С. 15-22. DOI: 10.30713/0207-2351-2020-12(624)-15-22
- Zhiping Chen, Jia Zhang, Daren Zhang et al. Enhanced permeability prediction in porous media using particle swarm optimization with multi-source integration // Artificial Intelligence in Geosciences. 2024. Vol. 5. № 100090. DOI: 10.1016/j.aiig.2024.100090
- Zhuoheng Chen, Hannigan P. A shale gas resource potential assessment of Devonian Horn River strata using a well-performance method // Canadian Journal of Earth Sciences. 2016. Vol. 53. № 2. P. 156-167. DOI: 10.1139/cjes-2015-0094
- Муслимов Р.Х. Становление и перспективы дальнейшего развития гидродинамических методов разработки нефтяных месторождений России // Нефтяное хозяйство. 2020. № 12. С. 96-100. DOI: 10.24887/0028-2448-2020-12-96-100
- Пискунов С.А., Давуди Ш. Прогнозирование дебита горизонтальных скважин с применением модели машинного обучения // Известия Томского политехнического университета. Инжиниринг георесурсов. 2024. Т. 335. № 5. С. 118-130. DOI: 10.18799/24131830/2024/5/4553
- Ben-Awuah J., Padmanabhan E. An enhanced approach to predict permeability in reservoir sandstones using artificial neural networks (ANN) // Arabian Journal of Geosciences. 2017. Vol. 10. Iss. 7. № 173. DOI: 10.1007/s12517-017-2955-7
- Elkatatny S., Mahmoud M., Tariq Z., Abdulraheem A. New insights into the prediction of heterogeneous carbonate reservoir permeability from well logs using artificial intelligence network // Neural Computing and Applications. 2018. Vol. 30. Iss. 9. P. 2673-2683. DOI: 10.1007/s00521-017-2850-x
- Irani R., Nasimi R. Evolving neural network using real coded genetic algorithm for permeability estimation of the reservoir // Expert Systems with Applications. 2011. Vol. 38. Iss. 8. P. 9862-9866. DOI: 10.1016/j.eswa.2011.02.046
- Bagheripour P. Committee neural network model for rock permeability prediction // Journal of Applied Geophysics. 2014. Vol. 104. P. 142-148. DOI: 10.1016/j.jappgeo.2014.03.001
- Matinkia M., Hashami R., Mehrad M. et al. Prediction of permeability from well logs using a new hybrid machine learning algorithm // Petroleum. 2023. Vol. 9. Iss. 1. P. 108-123. DOI: 10.1016/j.petlm.2022.03.003
- Xiaobo Zhao, Xiaojun Chen, Qiao Huang et al. Logging-data-driven permeability prediction in low-permeable sandstones based on machine learning with pattern visualization: A case study in Wenchang A Sag, Pearl River Mouth Basin // Journal of Petro-leum Science and Engineering. 2022. Vol. 214. № 110517. DOI: 10.1016/j.petrol.2022.110517
- Jing-Jing Liu, Jian-Chao Liu. Permeability Predictions for Tight Sandstone Reservoir Using Explainable Machine Learning and Particle Swarm Optimization // Geofluids. 2022. Vol. 2022. № 2263329. DOI: 10.1155/2022/2263329
- Tahmasebi P., Hezarkhani A. A fast and independent architecture of artificial neural network for permeability prediction // Journal of Petroleum Science and Engineering. 2012. Vol. 86-87. P. 118-126. DOI: 10.1016/j.petrol.2012.03.019
- Kumar A., Lin Liang, Ojha K. Simultaneous inversion of permeability, skin and boundary from pressure transient test data in three-dimensional single well reservoir model // Petroleum Research. 2024. Vol. 9. Iss. 2. P. 265-272. DOI: 10.1016/j.ptlrs.2024.01.004
- Aïfa T., Baouche R., Baddari K. Neuro-fuzzy system to predict permeability and porosity from well log data: A case study of Hassi R׳Mel gas field, Algeria // Journal of Petroleum Science and Engineering. 2014. Vol. 123. P. 217-229. DOI: 10.1016/j.petrol.2014.09.019
- Chaves G.S., Ferreira Filho V.J.M. Enhancing production monitoring: A back allocation methodology to estimate well flow rates and assist well test scheduling // Petroleum Research. 2024. Vol. 9. Iss. 3. P. 369-379. DOI: 10.1016/j.ptlrs.2024.03.008
- El-Sebakhy E.A., Asparouhov O., Abdulraheem A.A. et al. Functional networks as a new data mining predictive paradigm to predict permeability in a carbonate reservoir // Expert Systems with Applications. 2012. Vol. 39. Iss. 12. P. 10359-10375. DOI: 10.1016/j.eswa.2012.01.157
- Gholami R., Moradzadeh A., Maleki S. et al. Applications of artificial intelligence methods in prediction of permeability in hydrocarbon reservoirs // Journal of Petroleum Science and Engineering. 2014. Vol. 122. P. 643-656. DOI: 10.1016/j.petrol.2014.09.007
- Yanji Wang, Hangyu Li, Jianchun Xu et al. Machine learning assisted relative permeability upscaling for uncertainty quan-tification // Energy. 2022. Vol. 245. № 123284. DOI: 10.1016/j.energy.2022.123284
- Guoyin Zhang, Zhizhang Wang, Huaji Li et al. Permeability prediction of isolated channel sands using machine learning // Journal of Applied Geophysics. 2018. Vol. 159. P. 605-615. DOI: 10.1016/j.jappgeo.2018.09.011
- Sheykhinasab A., Mohseni A.A., Bahari A.B. et al. Prediction of permeability of highly heterogeneous hydrocarbon reservoir from conventional petrophysical logs using optimized data-driven algorithms // Journal of Petroleum Exploration and Production Technology. 2023. Vol. 13. Iss. 2. P. 661-689. DOI: 10.1007/s13202-022-01593-z
- Campos D., Wayo D.D.K., De Santis R.B. et al. Evolutionary automated radial basis function neural network for multiphase flowing bottom-hole pressure prediction // Fuel. 2024. Vol. 377. № 132666. DOI: 10.1016/j.fuel.2024.132666
- Anifowose F., Labadin J., Abdulraheem A. Improving the prediction of petroleum reservoir characterization with a stacked generalization ensemble model of support vector machines // Applied Soft Computing. 2015. Vol. 26. P. 483-496. DOI: 10.1016/j.asoc.2014.10.017
- Anifowose F.A., Labadin J., Abdulraheem A. Ensemble model of non-linear feature selection-based Extreme Learning Ma-chine for improved natural gas reservoir characterization // Journal of Natural Gas Science and Engineering. 2015. Vol. 26. P. 1561-1572. DOI: 10.1016/j.jngse.2015.02.012
- Otchere D.A., Ganat T.O.A., Gholami R., Lawal M. A novel custom ensemble learning model for an improved reservoir permeability and water saturation prediction // Journal of Natural Gas Science and Engineering. 2021. Vol. 91. № 103962. DOI: 10.1016/j.jngse.2021.103962
- Mkono C.N., Chuanbo Shen, Mulashani A.K., Nyangi P. An improved permeability estimation model using integrated ap-proach of hybrid machine learning technique and Shapley additive explanation // Journal of Rock Mechanics and Geotechnical Engi-neering. 2025. Vol. 17. Iss. 5. P. 2928-2942. DOI: 10.1016/j.jrmge.2024.09.013
- Shijia Ma, Jiangfeng Liu, Yuanjian Lin et al. Prediction of permeability of various geotechnical materials under different temperatures based on physical characteristics and machine learning // Fuel. 2025. Vol. 379. № 133109. DOI: 10.1016/j.fuel.2024.133109
- Riyadi Z.A., Olutoki J.O., Hermana M. et al. Machine learning prediction of permeability distribution in the X field Malay Basin using elastic properties // Results in Engineering. 2024. Vol. 24. № 103421. DOI: 10.1016/j.rineng.2024.103421
- Masroor M., Niri M.E., Sharifinasab M.H. A multiple-input deep residual convolutional neural network for reservoir permea-bility prediction // Geoenergy Science and Engineering. 2023. Vol. 222. № 211420. DOI: 10.1016/j.geoen.2023.211420
- Lawal A., Yingjie Yang, Hongmei He, Baisa N.L. Machine Learning in Oil and Gas Exploration: A Review // IEEE Access. 2024. Vol. 12. P. 19035-19058. DOI: 10.1109/ACCESS.2023.3349216
- Захаров Л.А., Мартюшев Д.А., Пономарева И.Н. Прогнозирование динамического пластового давления методами искусственного интеллекта // Записки Горного института. 2022. Т. 253. С. 23-32. DOI: 10.31897/PMI.2022.11
