Study of changes in the void space of core samples under cyclic loading
- 1 — Ph.D. Associate Professor Tyumen State University ▪ Orcid ▪ Elibrary
- 2 — Specialist Tyumen Oil Research Centre ▪ Orcid
- 3 — Postgraduate Student Tyumen State University ▪ Orcid
- 4 — Chief Specialist Tyumen Oil Research Centre ▪ Orcid
Abstract
The subsurface state is explored and analysed by studying the core material. This is the basis for forecasts, construction and improvement of models. The reservoir properties of rocks obtained from the laboratory study of sample are subject to a system error caused by three main factors: rock selection in the zone of altered stress-strain state, rock removal from the thermobaric conditions of natural occurrence, and the measuring equipment error. A change in the natural stress-strain state of rocks occurs as a result of intervention in the formation system and the entire massif by constructing a well, creating overburden and depression. The rise of the core causes unloading from formation pressure to atmospheric one, natural saturation is lost, temperature conditions change. This affects the reservoir properties and rock injectivity. This study is aimed at investigating changes in the void space of the rock in formation conditions under cyclic loading. Based on the data obtained, a regression forecast of properties is made, excluding external influences. The article describes the results of experiments on multiple loading and unloading of water-saturated sandstone samples by geostatic pressure with precise control of the water displaced and returned to the void space. This method enables us to record the change in the internal void volume of the rock and, as a consequence, elastic and plastic deformations, the value of relaxation of elastic deformations. The dynamics of change in the coefficients of porosity and compressibility from the stress state cycle is estimated and the range of predicted porosity values of the rock in formation conditions is determined. For samples of permeable medium- to fine-grained sandstone, the obtained character of porosity change gives a forecast of the initial porosity in formation conditions of 20.19±0.61 %. Thus, the exclusion of human impact on porosity gives values 1.42 % higher than the results of standard laboratory studies.
Funding
The work was carried out under the State assignment in the field of science for the implementation of scientific projects by teams of youth laboratories of higher education institutions subordinate to the Ministry of Education and Science of Russia, under the project “Development of a system for monitoring, assessing, and forecasting the overall state of the components of the “water – rock – gas – organic matter” system during the exploitation of hydrocarbon fields” (project N FEWN-2023-0011).
Introduction
Construction of underground structures and wells requires a detailed study of geodynamic and geomechanical factors, which significantly affect the economic indicators of subsurface development. At the stage of oil and gas field exploration, geophysical methods are used to determine the composition and properties of rocks and formation fluids [1, 2]. Comprehensive interpretation of logs requires a search for relationships between measured geophysical parameters, lithostructural characteristics of reservoir rocks and their petrophysical properties.
Petrophysics allows us to study the properties of rocks, their dependencies, and the nature of their interaction with formation fluids. Fundamental concepts of the physical characteristics of porous media and the study of their dependence on various changing factors are presented in [3].
A naturally occurring formation undergoes changes in the stress-strain state during exploration activities; the hydrodynamic regime changes. These processes affect the operational characteristics of reservoir beds [2]. The appearance and development of fractures at the micro- and macrolevels, changes in the grain arrangement, and changes in the pore space structure are associated with the redistribution of stresses caused by the mode of load application – the production conditions [2, 4, 5]. Heterogeneous reservoir structure complicates the system and further forecasts of its behaviour. This leads to a comparison and reassessment of approaches to the study and application of filtration-capacitive and deformation-strength properties of rocks [6, 7].
Permeability of fractured reservoirs is particularly susceptible to abrupt changes in the stress field. Tests conducted in injection and production wells show that permeability strongly depends both on the effective pressure and the rate of its change [8].
The capacitive properties of the rock are determined by the presence of void spaces: pores, caverns, fractures. Each type of void space is classified by size, geometry, as well as the nature of the mutual connection and movement of fluids in the rock. Such a division is described in [9, 10].
A core (a rock sample) provides information in the laboratory through a series of studies that cannot yet be reliably obtained by other methods (for example, geophysical studies in wells). The correct approach to planning a set of studies can affect the quality of the interpreted data [11, 12].
Currently, many works have been published that present different methods for assessing and studying the porosity of different types of reservoirs [5, 13-16]. Modern information technologies do not bypass this area. Large accumulated data volumes and sets of correlations allow, through machine learning – neural networks – to predict petrophysical parameters [17, 18].
Compressibility and elasticity characterize the ability of rocks to restore their original shape and volume after external mechanical action [19, 20]. The volumetric elasticity index is determined by the compressibility coefficient, which, in turn, is a derivative of the relative change in porosity depending on the effective pressure [6]. Compressibility and elasticity are used to analyse deformation and strength characteristics, which is an important aspect of hydrocarbon field development [20-23].
Many researchers have introduced relationships between pore compressibility, porosity, and other mechanical properties of rocks in the form of analytical correlations or developed empirical formulas to estimate compressibility by comparing model estimations with experimental data [3, 19, 24].
There are different methods for determining the volume compression of rocks caused by changes in the stress state. For example, [7] gives the integral and differential approaches. The influence of the pore type on compressibility with a change in effective stress is given in [24, 25]. The prediction of pore compressibility using an empirical relationship based on the total effective stress and initial porosity is shown in [19]. The analysis of a large number of rock tests in [6, 19] reduced the random error to a minimum and made it possible to determine that the maximum compressibility coefficient is observed at low porosity values.
The assessment of geological reserves is associated with a number of uncertainties, one of which is the filtration and capacity properties. If the assessment is performed with an error rate exceeding the limits set by regulations, the error will ultimately affect the quality of forecasting the development indicators, which may lead to a decrease in critically important economic indicators. Accounting for and reducing each of the possible factors reduces the probability of such an outcome. The factors include porosity, the initial value of which plays an important role for formation conditions, since a distortion of this parameter even by 1 % can lead to an error of thousands of tons.
To assess the nature of the change in porosity and its subsequent forecast, the following tasks were set: using the example of a typical representative of a terrigenous reservoir – sandstone, which is characteristic of the Volga-Ural petroleum province in composition and properties, to develop a method for laboratory determination of the initial porosity and compressibility values of a rock sample, which it possessed before human impact; to assess the errors in determining the porosity coefficient obtained in standard studies, in comparison with the predicted value of rock porosity; to correlate changes in plastic and elastic deformations of the rock under cyclic loading – unloading.
Methods
Research methods
Changes in the stress-strain state of rocks during field development inevitably affect reservoir properties in the bottomhole zone [26, 27]. Consequently, the use of sample data from such an influence zone will affect the accuracy of modelling, development, and evaluation of reserves. In the work, the influence of pressure changes in a well on the rock is modelled by means of a gradual increase and subsequent decrease in the pressure acting on the sample, while the impact is partitioned, i.e. stepwise.
The essence of the experiment: a rock sample is placed in the unit at full saturation with formation fluid of natural mineralization. The influence of increase and decrease cycles of the effective triaxial axisymmetric pressure on open porosity and compressibility is studied in the created formation pressure and temperature (P-T) conditions. Loading is smooth, sustained until the following values are reached
The increase and decrease of the effective pressure Pef is achieved by changing the overburden (rock) pressure Pov with the pore (formation) Ppor constant. The reliability of such a simplification for sandstones is shown in [27].
When exposed, elastic and inelastic deformations are formed in the rock sample. The latter causes a shift in the loading and unloading curves (Fig.1). When such loadings are repeated, plastic deformations will accumulate with each cycle to a certain limit state. In the case of highly porous samples (18-30 %), compaction occurs. Additional deformation is accompanied by the appearance of new and the development of old defects, and low-porosity rocks (0.36-7.4 %) are loosened [14].
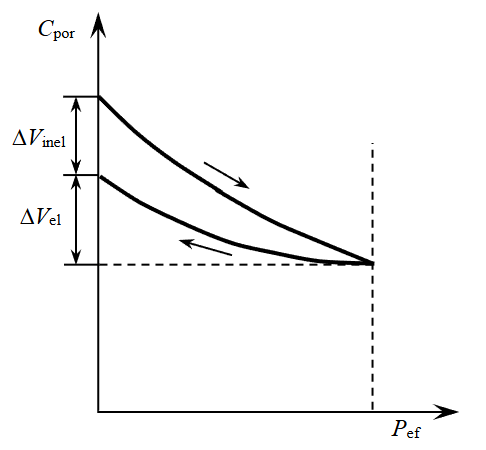
Fig.1. The influence of deformations during the loading cycle on the coefficient of open porosity of the rock Cpor; ∆Vel and ∆Vinel are the elastic and inelastic deformations of the pores in the sample
To create loading and unloading in P-T conditions, specialized process equipment is used. The basic operating principle of the unit is to measure the volume of fluid displaced from the pore space of the rock under the created modelling pressures. The samples under study must be completely saturated with fluid. The unit is a pneumohydraulic system of two branches (Fig.2) controlled by pneumatic valves V1-4. The left one, by means of a saturating fluid, forms pore pressure in the sample, measured by the Ppor1 transducer. The Ppor2 meter allows determining the pore pressure at the sample outflow for measuring permeability. The right branch operates with hydraulic oil, creating an overburden pressure measured by the Pov1 pressure transducer. The overburden pressure equally affects the lateral surface of the rock sample through a rubber cuff and creates an axial load by means of a hydraulic cylinder located at the end of the core holder (CH).
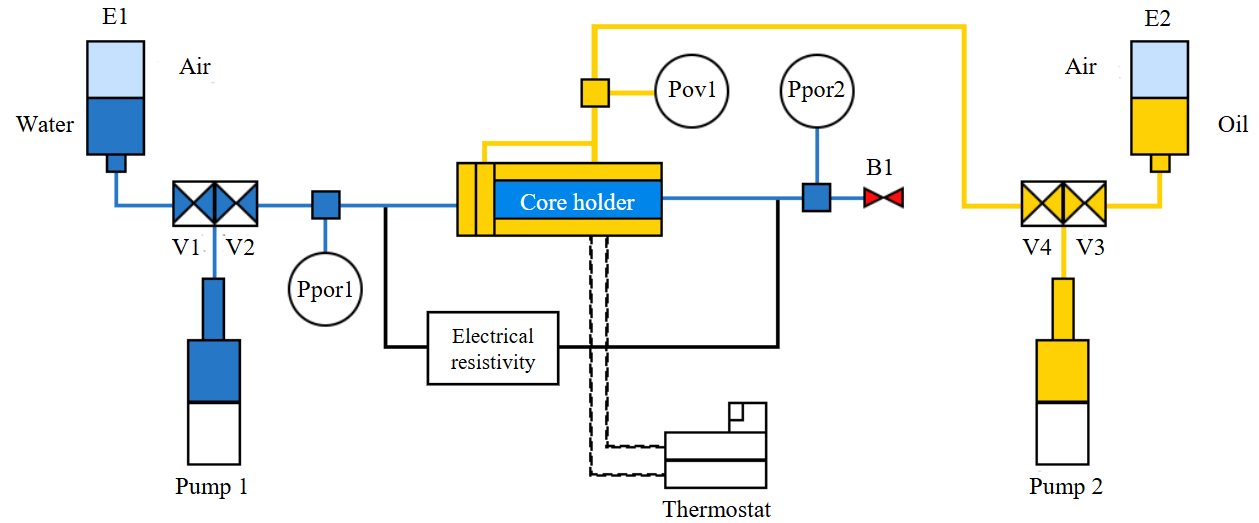
Fig.2. Simplified pneumohydraulic diagram of the core testing unit
Study of samples for porosity
Desalted dry samples are additionally dried to constant mass, then weighed, giving mass M1. The length L and diameter D of the sample are measured with a calliper, the average value for three measurements is taken. The saturating liquid and samples are separately vacuumized, then the rock is saturated by the capillary impregnation method. The samples are weighed in the saturation liquid, giving mass M2, and in air, giving mass M3.
Based on the data obtained, the following are estimated:
sample volume
coefficient of open porosity in atmospheric conditions
open pore volume
Investigation of open porosity and compressibility of samples
Before placing the sample in the unit, the open porosity is measured in atmospheric conditions using the described method. Then the core is moved to a dry and clean CH (Fig.2). The rock is additionally saturated and air is removed from the unit system. The overburden pressure Pov = 3 MPa is set for tight adhesion of the rubber cuff to the sample surface; a pore pressure of Ppor = 1 MPa is created at the end of the sample; the opposite side is depressurized by means of a needle valve B1 and communicates with the atmosphere, thus creating a pressure difference and filtration in an amount of at least two pore volumes.
At the end of filtration, the pressures are set as follows: pore Ppor, equal to the formation pressure, and initial overburden Pov 2 MPa higher. Temperature and electrical resistance become stable at these values.
The samples are loaded stepwise, from the initial overburden pressure, passing through the isostatic pressure value, to a pressure equal to the geostatic pressure. At the first loading step, the counter of the displaced liquid volume is reset. The pressure is raised to the next step. At each compression step, the sample is held until all parameters are stabilized: temperature, electrical resistivity, and volume of liquid displaced from the sample – the data are recorded. After achieving formation pressure conditions, the sample is unloaded. The unloading occurs with a stepwise decrease in Pov. Upon completion of the loading and unloading cycle, the sample is removed from the CH, its open porosity is measured in atmospheric conditions. Then the sample is held in a closed container with a saturating fluid for subsequent relaxation, which takes at least two weeks for sandstones. Then the loading cycle is repeated.
Materials
In order to collect statistics and obtain a range of close values within one pay formation, a number of criteria for selecting samples for investigations were compiled: belonging to a single formation – the same P-T conditions and lithological composition for the entire group, close removal depths (within 5 m), close predetermined porosity and permeability values between samples.
Samples of porous fine- to medium-grained sandstone with carbonized plant detritus were selected from a well of one of the Volga-Ural petroleum province fields from a depth of 2300 m. The properties of the selected samples are presented in the Table. Physical geological characteristics of the pay formation of the studied target: formation pressure 22.9 MPa; isostatic pressure 37.8 MPa; rock pressure 58.8 MPa; formation temperature 47 °С; mineralization 272.1 g/dm3.
Properties of rock samples in atmospheric conditions
|
Sample number |
Helium porosity, % |
Permeability, mD |
|
75 |
19.4 |
842.8 |
|
77 |
19.8 |
878.7 |
|
95 |
19.1 |
822.2 |
|
Average value |
19.4 |
847.9 |
Data analysis
Figure 3 shows the dynamics of Vpor change as a result of the effective pressure action cycle from 2 to 35.9 MPa. During loading, the effective pressure increases, the sample is compressed, and its pore volume decreases. The pore line pump operates in the pressure holding mode at 22.9 MPa. A decrease in Vpor provokes pressure increase in the pore line, which is recorded by the sensors and compensated by the pump. The volume of liquid pumped out by the pump to compensate for the pressure characterizes the changes in the pore volume ΔVpor. This process is shown by blue dots 1 through 2 (Fig.3), the latter corresponding to the maximum effective pressure of 35.9 MPa. Arrow 4 indicates an increase in ΔVpor, which is caused by elastic and inelastic deformations of the pore space. The difference in values between points 1 and 2 corresponds to the total change in pore volume, equal to the sum of the changes in volume due to elastic and inelastic deformations of the pores:
During unloading, due to elastic deformations ΔVel, the rock tends to return to its original shape. As a result, Vpor increases, and the pressure in the pore line decreases. ΔVpor values are indicated by red experimental points, the decrease is compensated by the pump along arrow 5 (Fig.3). Weakening of the effective pressure to 2 MPa corresponds to point 3, where the proportion of elastic deformations of the rock volume is minimal, but there remains an inelastic change in ΔVinel formed under loading.
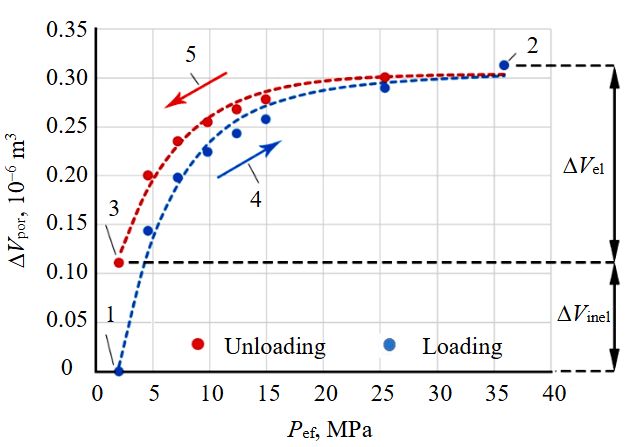
Fig.3. Dependence of the displaced volume of the saturating fluid on the effective pressure using sample 95 as an example
The coloured dotted curves in Fig.3 show the functional dependence starting from the moment of drainage (point 1). The approximation is made by the nonlinear least squares method in the CurveExpert software package. The exponential function that best satisfies the low error condition for the obtained data set is taken as the model:
where A, B, C are the numerical approximation coefficients.
The values of the approximating function are used in subsequent estimations. The change in the pore compressibility coefficient is determined based on the data set of changes in Vpor against Pef in the cycle:
Change in the porosity coefficient under isostatic pressure:
The porosity coefficient is measured after the cycle and relaxation of the sample using formulas (1)-(3).
The obtained approximation data allow us to plot a graph of the Cpor dependence of the studied samples in the created P-T conditions on the applied Pef at each cycle.
As an example, Fig.4 shows the loading and unloading curves for the first cycle of sample 95. From the curves of one cycle, it is evident that the main change in pore volume occurs up to Pef = 15 MPa, after which the curve becomes flat and the parameter changes little with pressure. These plastic deformations clearly show the discrepancy between the loading and unloading curves in Fig.4. The porosity in the sample after the cycle, when measured in atmospheric conditions, decreased by 0.44 % of the absolute value, while during the cycle itself, the porosity decreased by 1.26 %. A similar analysis is valid for loadings and other samples of the lithological group under consideration. The conclusions drawn coincide with a number of experiments conducted by V.M.Dobrynin [28], A.T.Karmansky [29], V.S.Zhukov [30-32].
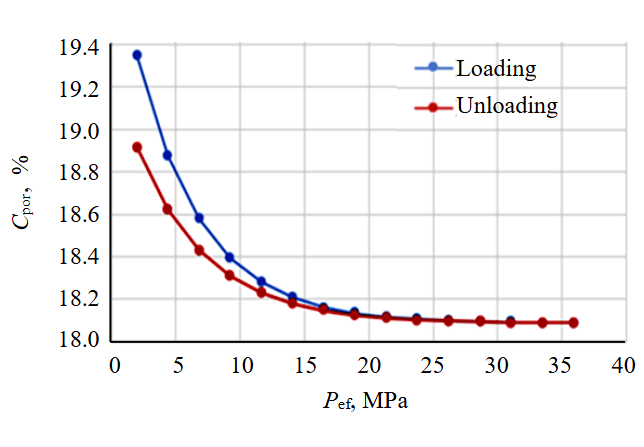
Fig.4. Change in the porosity coefficient at the first loading cycle of sample 95
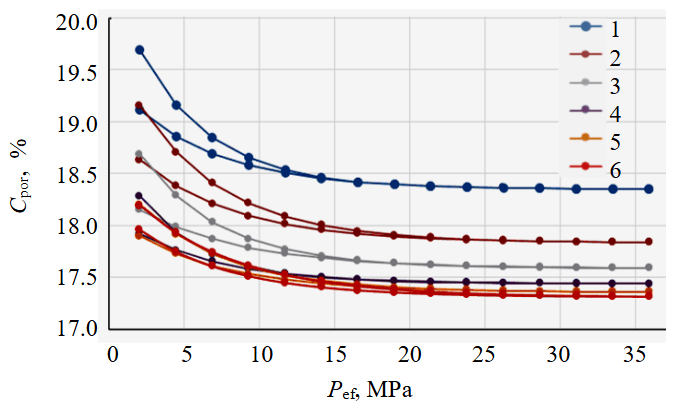
Fig.5. Degradation of the porosity coefficient under cyclic rock loading
1-6 – cycle numbers
Experiments with several samples allows us to obtain a data set with average representative values of the studied parameters for a given group.
Discussion
Based on averaged data from the samples, a general graph is plotted that characterizes the changes in the porosity coefficient against the effective pressure under the effect of loading/unloading on permeable sandstones with similar lithology (Fig.5).
The curves of porosity change in Fig.5 converge with each cycle. A decaying nature of the change is observed, which indicates rock compaction. Numerous experiments on cyclic volumetric deformation of rocks confirm the compaction of highly porous rocks, the effective porosity of which varies within 18-30 % [14]. The decrease in porosity reaches 1 %, the relative change is 5.45 %. The curves do not close down between the cycles in the left part of Fig.5 due to relaxation of the samples between experiments, i.e. residual elastic deformations after loading partially restore the pore volume when the samples rest in the saturating fluid between experiments.
Multiple repetition of loads subjects residual deformations to ever less changes. At a certain cycle, their accumulation becomes unnoticeable, as a result of which all subsequent loops are superimposed (Fig.5, cycles 5 and 6).
The laboratory value of porosity corresponds to 18.77 %. It appears at an effective pressure in the unit equal to the difference between the formation and isostatic pressures.
With six load cycles, each effective pressure corresponds to six values of the porosity coefficient. Based on this data set, using software, a forecast of the rock properties is made, theoretically excluding human impact. For each pressure stage, a graph of the porosity coefficient y against the cycle number x is plotted. In accordance with this, an approximation is made:
The obtained set of forecast points allows us to construct an averaging curve (Fig.6). According to it, under the current isostatic pressure, the porosity value is 20.19 %. The uncertainty of the value for the studied group of samples is considered by the interval of probable values, which is constructed considering the maximum and minimum values of the cycles for each of the samples according to the approximation. For the previously determined porosity, the error is ±0.61 % (4).
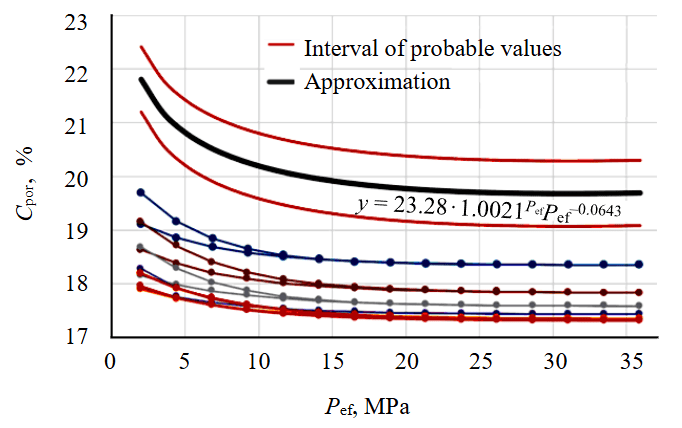
Fig.6. Initial porosity prediction curve based on cyclic loading statistics
The approximation curve is described with a high degree of reliability by formula (4). According to experimental data, the coefficients are: A = 23.28; B = 1.0021; C = –0.0643.
Due to plastic deformations causing the curves to diverge, with a decrease in pressure, the porosity in the sample also decreases in atmospheric conditions. At the same time, the compressibility of the pores and the entire rock sample decreases. The results of the primary data approximation allow us to study the dependence of the compressibility coefficients β, βpor, βsol of the rock, pores, and solid phase, respectively.
Compressibility of the solid skeleton, compared to that of the pores, is extremely small. This is confirmed by V.M.Dobrynin [28], who concluded that βsol value for sand and carbonate petroleum reservoirs is one to two orders of magnitude lower than the pore compressibility coefficient. Therefore, when performing many estimations, the value of the solid phase compressibility coefficient can be taken as constant with high accuracy for this type of reservoir.
Averaging the data for the group for each cycle results in a general graph that characterizes the changes in the pore compressibility coefficient against the effective pressure upon exposure of permeable sandstone to loading/ unloading (Fig.7).
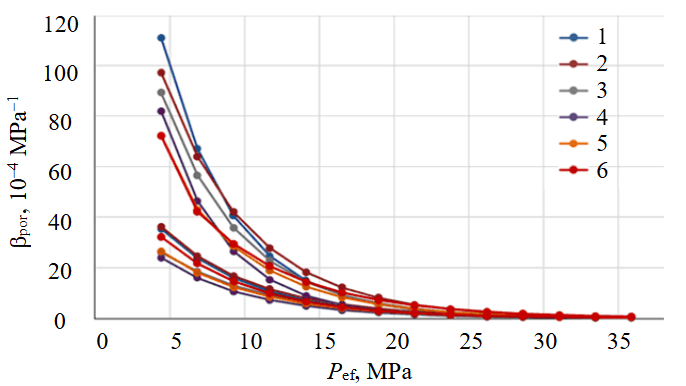
Fig.7. Averaged over a group of samples, degradation of pore volume compressibility bpor against pressure Pef
1-6 – cycle numbers
The compressibility change loops are less pronounced on the right side, and the difference is only apparent at low pressures. Thus, in absolute terms, the maximum change in compressibility at the initial effective pressure is 74.753∙10–4 MPa–1, which is two orders of magnitude higher than the change in compressibility at the maximum pressure action of 0.548∙10–4 MPa–1. As a result of six loads, the compressibility irreversibly decreased (considering subsequent relaxation) by 34.9 %. The role of elastic deformations in the relaxation of samples after loading is great. Using the example of the first cycle, compared to the values of the second one, the sample restored its pore volume by 87.7 %, while the pore volume irreversibly changed by 12.3 %.
Scientific novelty
Studying the nature of decreasing rock properties under cyclic impact and its subsequent forecast allows increasing the accuracy of determining reservoir properties based on core data. These data can improve the quality of modelling the processes occurring in the near-wellbore area and the accuracy of the reserves assessment, as well as prevent a decrease in reservoir properties.
Conclusion
A series of experiments were conducted to study changes in the void space of core samples in reservoir conditions under cyclic axisymmetric loading, to predict porosity and to assess the nature of the impact on it. Typical representatives of terrigenous reservoir rocks were used as samples. Their composition and petrophysical properties are typical of the Volga-Ural petroleum province.
A method was developed to determine the nature of changes in porosity under cyclic loads and that of deterioration in rock properties. The effect of cyclic loading was estimated, and a forecast was made taking this into account, restoring the porosity value corresponding to the natural occurrence of rock in the formation. Estimation expressions were proposed and the experimental results were presented graphically. The difference between the porosity coefficient obtained in standard studies and the predicted value of rock porosity was determined. The relationship and change of plastic and elastic deformations of core pores under cyclic loads were considered.
With increasing pressure of triaxial compression, the differences between the compressibility coefficients during cyclic compaction are minimal. In conditions of increasing load on the rock, porosity decreases. With multiple repetition of the load, each subsequent cycle is ever less susceptible to accumulation of residual deformations, and therefore the hysteresis loops converge. Rock compacted by repeated loads to such a state exhibits only elastic deformations if the acting pressures are not exceeded. Small values of compressibility change in formation P-T conditions, as well as a high error in their determination make it difficult to predict. The porosity forecast shows that for the selected group of rock this value is 20.19±0.61 %, while the values of the standard laboratory test are 18.77 %, which is 1.42 % less.
References
- Kashnikov Yu.A., Ashikhmin S.G. Rock mechanics in petroleum industry. Moscow: Nedra-Biznestsentr, 2007, p. 467 (in Russian).
- Zhukov V.S., Semenov Ye.O., Kuzmin Yu.O. Dynamics of physical properties of reservoirs at development of oil and gas fields. Vesti gazovoy nauki. 2018. N 5 (37), p. 82-89 (in Russian).
- Avchyan G.M., Matveenko A.A., Stefankevich Z.B. Petrophysics of sedimentary rocks in subsurface conditions. Moscow: Nedra, 1979, p. 224 (in Russian).
- Blinova E.Yu., Indrupskiy I.M., Zakirov E.S., Kovalenko K.V. Accounting for spatial heterogeneity of reservoir elastic properties in reservoir simulation. Georesources, Geoenergetics, Geopolitics. 2012. N 1 (5) (in Russian).
- Maximov V.M., Mikhailov N.N. Experimental study of porous media deformations at cyclic load. Poromechanics: Proceedings of the Biot Conference on Poromechanics, 14-16 September 1998, Louvain-la-Neuve, Belgium. Rotterdam: A.A. Balkema, 1998, p. 605-607. DOI: 10.1201/9781003078487-102
- Galkin S.V., Krivoshchekov S.N., Kozyrev N.D. et al. Accounting of geomechanical layer properties in multi-layer oil field development. Journal of Mining Institute. 2020. Vol. 244, p. 408-417. DOI: 10.31897/PMI.2020.4.3
- Zhukov V.S., Kuzmin Yu.О. Comparison of the approaches to assessing the compressibility of the pore space. Journal of Mining Institute. 2022. Vol. 258, p. 1008-1017. DOI: 10.31897/PMI.2022.97
- Zhaoping Meng, Jincai Zhang, Rui Wang. In-situ stress, pore pressure and stress-dependent permeability in the Southern Qinshui Basin. International Journal of Rock Mechanics and Mining Sciences. 2011. Vol. 48. Iss. 1, p. 122-131. DOI: 10.1016/j.ijrmms.2010.10.003
- Kuzmin Yu.O. Deformational consequences of oil and gas field development. Geophysical Processes and Biosphere. 2021. Vol. 20. N 4, p. 103-121 (in Russian). DOI: 10.21455/GPB2021.4-7
- Sharifi J. Multi-pore rock physics model: An intelligent approach for carbonate rocks. Journal of Petroleum Science and Engineering. 2022. Vol. 218. N 111002. DOI: 10.1016/j.petrol.2022.111002
- Schön J.H. Physical properties of rocks. Fundamentals and Principles of Petrophysics. Elsevier, 2015, p. 512.
- Kalcheva A.V. The core as one of the main sources of geological data. Georesursy. 2009. N 3 (31), p. 23-26 (in Russian).
- Kam Ng, Santamarina J.C. Mechanical and hydraulic properties of carbonate rock: The critical role of porosity. Journal of Rock Mechanics and Geotechnical Engineering. 2023. Vol. 15. Iss. 4, p. 814-825. DOI: 10.1016/j.jrmge.2022.07.017
- Kolchitskaya T.N., Mikhailov N.N. The influence of cyclic well production conditions on changes in the state of petroleum formations. Geologiya, geofizika i razrabotka neftyanykh i gazovykh mestorozhdenii. 2002. N 5, p. 81-84 (in Russian).
- Mangione A., Lewis H., Geiger S. et al. Estimation of pre-dolomitisation porosity and permeability of a nummulitic carbonate reservoir rock using the Multi-Component Architecture Method (MCAM). Marine and Petroleum Geology. 2021. Vol. 132. N 105196. DOI: 10.1016/j.marpetgeo.2021.105196
- Qigui Tan, Lijun You, Yili Kang et al. Changes in pore structures and porosity-permeability evolution of saline-lacustrine carbonate reservoir triggered by fresh water-rock reaction. Journal of Hydrology. 2020. Vol. 580. N 124375. DOI: 10.1016/j.jhydrol.2019.124375
- Kushwaha P.K., Maurya S.P., Rai P., Singh N.P. Chapter 15 – Prediction of petrophysical parameters using probabilistic neural network technique. Basics of Computational Geophysics. 2021, p. 273-292. DOI: 10.1016/B978-0-12-820513-6.00019-9
- Chicheng Xu, Lei Fu, Tao Lin et al. Machine learning in petrophysics: Advantages and limitations. Artificial Intelligence in Geosciences. 2022. Vol. 3, p. 157-161. DOI: 10.1016/j.aiig.2022.11.004
- Fjær E. Relations between static and dynamic moduli of sedimentary rocks. Geophysical Prospecting. 2019. Vol. 67. Iss. 1, p. 128-139. DOI: 10.1111/1365-2478.12711
- Vavilin V.A., Romanov Yu.K., Galiev T.R., Suleimanov R.F. On an alternate technique to determine elasticity limit of the rocks under simulated reservoir conditions. Georesursy. 2008. N 5 (28), p. 44-48 (in Russian).
- Sharifi J., Saberi M.R. Quantitative Evaluation of Fracture Porosity in a Carbonate Reservoir Using Analytical Method. 83rd EAGE Annual Conference & Exhibition, 6-9 June 2022, Madrid, Spain. European Association of Geoscientists & Engineers, 2022. Vol. 2022, p. 5. DOI: 10.3997/2214-4609.202210135
- Zhukov V.S., Ivanov P.Yu. Changes in the physical properties of a reservoir as a result of an increase in effective pressure during field development (modelling using the example of the Yuzhno-Kirinskoe field). Vesti gazovoi nauki. 2015. N 4 (24), p. 144-148 (in Russian).
- Sharifi J., Saberi M.R., Javaherian A., Moghaddas N.Н. Investigation of static and dynamic bulk moduli in a carbonate field. Exploration Geophysics. 2021. Vol. 52. Iss. 1, p. 16-41. DOI: 10.1080/08123985.2020.1756693
- Farahani M., Aghaei H., Saki M., Asadolahpour S.R. Prediction of pore volume compressibility by a new non-linear equation in carbonate reservoirs. Energy Geoscience. 2022. Vol. 3. Iss. 3, p. 290-299. DOI: 10.1016/j.engeos.2022.04.005
- Farahani M., Aghaei H., Masoumi H. Effect of pore type on porosity, permeability and pore volume compressibility of geological formations due to in-situ stress change. Journal of Petroleum Science and Engineering. 2022. Vol. 218. N 110986. DOI: 10.1016/j.petrol.2022.110986
- Vinogradov K.E., Pustoshkin R.V., Rodionov S.P. Features of accounting the hysteresis of permeability and compressibility of the porous space of low-permeable reservoirs during hydrodynamic modeling. Geology, geophysics and development of oil and gas fields. 2021. N 11 (359), p. 35-38. DOI: 10.33285/2413-5011-2021-11(359)-35-38
- Zheltov Yu.P. Deformations of rocks. Moscow: Nedra, 1966, p. 198 (in Russian).
- Dobrynin V.M. Deformations and changes in the physical properties of petroleum reservoirs. Moscow: Nedra, 1970, p. 239 (in Russian).
- Karmansky A.T. Collecting properties of rocks in changes of stress state type. Journal of Mining Institute. 2009. Vol. 183, p. 289-292 (in Russian).
- Zhukov V.S. Evaluation of changes in the physical properties of reservoirs caused by petroleum field development. Mining Informational and Analytical Bulletin. 2010. N 6, p. 341-349 (in Russian).
- Zhukov V.S. Laboratory modelling of reservoir pressure reduction during petroleum field development. Burenie i neft. 2006. N 1, p. 8-9 (in Russian).
- Zhukov V.S., Motorygin V.V., Pimenov Yu.G., Abrosimov A.A. Changes of porous space structure in reservoirs of Tala horizon at transition from atmospheric conditions to in-situ ones. Vesti gazovoy nauki. 2017. N 2 (30), p. 83-92 (in Russian).
