Модель движения земной коры в ITRF2020 – исследование на примере Северного Вьетнама

Буй Тхи Хонг Тхам; Фи Чыонг Тхань

Том 271

Страницы:

120-130

Скачать том:

RUS ENG

Научная статья

Геотехнология и инженерная геология

Модель движения земной коры в ITRF2020 – исследование на примере Северного Вьетнама

Авторы:

Буй Тхи Хонг Тхам¹

Фи Чыонг Тхань²

Об авторах

1 — Ph.D. декан Ханойский университет природных ресурсов и окружающей среды ▪ Orcid
2 — декан Ханойский университет природных ресурсов и окружающей среды ▪ Orcid

Дата отправки:

2023-10-04

Дата принятия:

2024-09-24

Дата публикации онлайн:

2024-12-24

Дата публикации:

2025-02-25

Аннотация

Значение скорости движения земной коры на севере Вьетнама, достигшее 38 единиц ГНСС по различным версиям Международной земной системы координат (ITRF2000, ITRF2005, ITRF2008), приведено к последней версии ITRF2020. Величина скорости движения земной коры унифицирована в динамической системе координат. Исследования показывают, что скорость движения земной коры составляет около 35 мм/год, а направление движения – с северо-запада на юго-восток. Для построения модели движения земной коры в северной части Вьетнама произведена высокоточная оценка данных о скорости движения коры с 38 станций, работающих в ITRF2020. Модель скорости движения земной коры построена с использованием метода коллокации в виде функции Маркова 3-го порядка. Использовались данные 34 из 38 станций, остальные четыре применялись в качестве контрольных. Скорость движения коры составляет 2 мм/год, направление смещения 2 град. Модель является первой моделью движения земной коры на севере Вьетнама, построенной в динамической системе координат ITRF2020. Результаты исследования применимы для теоретического и практического изучения движения земной коры. Этапы построения модели скорости движения, рассмотренные в работе, могут быть использованы в других исследованиях на территории Вьетнама.

Область исследования:

Геотехнология и инженерная геология

Ключевые слова:

скорость движения Северный Вьетнам Международная земная система координат ITRF2020 коллокация движение земной коры

Введение

Глобальная навигационная спутниковая система (ГНСС) широко используется для мониторинга сдвижения земной коры [1-3] и помогает прогнозировать и предупреждать землетрясения [4-6] и тектонические подвижки [7-9]. Временной ряд координат ГНСС используется для моделирования сдвижения земной коры [10-12]. Применение временных рядов для определения подвижек земной коры с помощью непрерывных ГНСС-измерений отражено в источниках [13-15]. Аналогично определяются горизонтальные подвижки земной коры в северо-восточной области Вьетнама, с использованием периодических GPS-измерений [16, 17].

ГНСС-технология использовалась во Вьетнаме для изучения подвижек земной коры с 1990-х годов. Скорость подвижек фиксировалась в различных динамических системах координат (ITRF94, ITRF2000, ITRF2005, ITRF2008, ITRF2014). В результате были получены различные непостоянные значения скорости, что в свою очередь осложняло построение модели. Для построения модели скорости подвижек значения, полученные на ГНСС-станциях, перенесены в аналогичную систему координат для последующего моделирования. Существует два способа переноса координат – сбор и переработка всех данных в единой системе координат, регистрация значений скорости подвижек со станций с параллельным внесением корректировок. Первый способ является сложным и трудозатратным [18-20], второй – более быстрый и точный [21-23]. В данной работе использован второй способ переноса значений скорости подвижек земной коры в единую динамическую систему координат ITRF2020 – последнюю версию ITRF, наиболее точную по сравнению с ранними [24-26]. Система координат ITRF2020 вышла в 2021 г. Параметры перевода координат между ITRF2020 и другими версиями системы можно найти на веб-сайте. Для моделирования скорости движения земной коры используется метод коллокации наименьших квадратов [27-29]. Это математическая функция с высокой степенью точности и надежности.

Для исследования скорости движения земной коры выбраны ГНСС-станции, использующие различные версии системы ITRF на севере Вьетнама:

в системе ITRF2000 ГНСС-станций, необходимых для изучения системы разломов Красной реки, разлома Дьен Бьен Фу, разлома реки Сон Да [30];
системе ITRF2005 ГНСС-станций Вьетнама, являющихся частью Азиатско-Тихоокеанской сети (PCGIAP) [31];
системе ITRF2005 станции DGNSS/CORS, которая входит в военную систему координат [32];
системе ITRF2008 ГНСС-станций, входящих в геодинамическую сеть по зонам разломов в северо-западной части Вьетнама и используемых для прогноза стихийных бедствий.

Методология

Построение модели скорости подвижек земной коры в единой системе координат выполнено следующим образом: скорость движения земной коры в различных системах координат приводится к показателям единой системы; далее показатели исследуются и моделируются с помощью математической функции.

Перевод значений скорости подвижек между системами координат. Формула перевода координат из системы (I) в систему (II) в определенный момент времени t имеет следующий вид [23, 24]:

\begin{matrix} X (t) = X {(t)}_{(II)} + T (t) + D X {(t)}_{(I)} + R {(t)}^{T} X {(t)}_{(I)}; \\ R^{T} = R_{1}^{T} (R_{1}) R_{2}^{T} (R_{2}) R_{3}^{T} (R_{3}) = (\begin{matrix} 1 & - R_{3} & R_{2} \\ R_{3} & 1 & - R_{1} \\ - R_{2} & R_{1} & 1 \end{matrix}), \end{matrix}

где X_(II) – вектор координат в новой системе отсчета, X_(II)=[X;Y;Z]^T_(II) ;X_(I) – вектор координат в старой системе отсчета, X_(I)=[X;Y;Z]^T_(I) ; T – вектор перевода или смещения между системами координат, T = [T₁; T₂; T₃]^T; D – масштаб; R^T – матрица поворота осей координат между двумя системами; R₁, R₂, R₃ – малые углы поворота.

С точки зрения динамики T₁, T₂, T₃, R₁, R₂, R₃ и D рассматриваются как параметры, функционально зависящие от времени, и выражаются в линейной форме. Общее значение параметров i = 1-7 выражается производной первого порядка по времени

β_{i} (t) = β_{i} (t_{0}) + {\overset{\cdot}{β}}_{i} (t - t_{0}),

где β_i(t₀) – значение β_i в момент времени t₀.

Расчет преобразованной скорости между системами координат:

V (t) = [\begin{matrix} V_{X} (t) \\ V_{Y} (t) \\ V_{Z} (t) \end{matrix}],

где V(t) – вектор скорости координатного движения.

Матрица скорости движения преобразуется из V_X, V_Y, V_Z в V_E, V_N, V_U[33]

(\begin{matrix} V_{E} \\ V_{N} \\ V_{U} \end{matrix}) = (\begin{matrix} - \sin λ & \cos λ & 0 \\ - \cos λ \sin φ & - \sin λ \sin φ & \cos φ \\ \cos λ \cos φ & \sin λ \cos φ & \sin φ \end{matrix}) (\begin{matrix} V_{X} \\ V_{Y} \\ V_{Z} \end{matrix}),

где V_E, V_N, V_U – скорости подвижек в восточном, северном и вертикальном направлениях соответственно; φ – долгота; λ – широта.

Скорость горизонтального перемещения точки и азимут определяются по формулам:

\begin{matrix} V = \sqrt{V_{E}^{2} + V_{N}^{2}}; \\ A z = \arctan \frac{V_{E}}{V_{N}} . \end{matrix}

Оценка диапазона измеряемых значений. Имеется набор из наблюдаемых значений n скоростей V₁, V₂, …, V_n. Среднее значение наблюдаемой скорости определяется по формуле

V_{av} = \sum_{i = 1}^{n} V_{i} / n; (1)

поправочное число наблюдаемого значения iвычисляется по следующей формуле

v_{i} = V_{av} - V_{i}; (2)

отклонение рассчитывается с помощью уравнения

σ^{2} = \frac{\sum_{i = 1}^{n} v_{i}^{2}}{n - 1} . (3)

Стандартное отклонение σ, представляющее собой квадратный корень из значения погрешности, используется для оценки качества наблюдаемых данных. Часто выбирается значение 3σ, соответствующее вероятности проявления измененного ряда ~ 99,73 %.

Модель скорости подвижек. Предположительно имеется два набора случайных переменных:

наблюдаемые значения l₁, l₂, ..., l_q, представленные q-мерным вектором,

l = {[\begin{matrix} l_{1} & l_{2} & ... & l_{q} \end{matrix}]}^{T};

сигналы, которые должны быть определены как S₁, S₂, …, S_m и представлены m-мерным вектором,

S = {[\begin{matrix} S_{1} & S_{2} & ... & S_{m} \end{matrix}]}^{T} .

Наилучшая линейная оценка вектора S:

\hat{S} = C_{S l} C_{l l}^{- 1} l . (4)

Формула (4) называется интерполяцией по методу наименьших квадратов или коллокационной интерполяцией по методу наименьших квадратов. Для расчета необходимо определить ковариационные матрицы C_llи C_S_l. Cначала необходимо рассчитать экспериментальные значения ковариации. Следует обозначить значение l_iв точке i.

Экспериментальная ковариация зависит от расстояния k между парами точек P и Q и определяется по формуле

\begin{matrix} C_{S} = cov (d l_{i}, d l_{Q}) = \frac{1}{k} \sum_{i = 1}^{k} d l_{i}^{P} d l_{i}^{Q}; \\ d l_{i} = l_{i} - \frac{1}{n} \sum_{i = 1}^{n} l {}_{i} . \end{matrix}

Теоретическая ковариационная функция должна быть выбрана, исходя из закона вариации экспериментальных ковариационных значений, а параметры теоретической ковариационной функции следует определять с использованием метода аппроксимации.

В данном исследовании для создания модели скорости подвижек земной коры в экспериментальной части и ее направления используется функция Маркова 3-го порядка [34, 35]

C_{S} = C_{0} e^{- \frac{S}{L}} (1 + \frac{S}{L} + \frac{S^{2}}{3 L^{2}}),

где С₀ – параметр теоретической ковариационной функции; L – расстояние между отношениями.

Стандартное отклонение между теоретической ковариационной функцией и экспериментальной ковариацией определяется по формуле

μ = \sqrt{\frac{\sum_{i = 1}^{k} ε_{i}^{2}}{k - 2}}, (5)

где ε_i – отклонение между теоретической ковариационной функцией и экспериментальной ковариацией в i-й точке; k – значения экспериментальной ковариации на определенном расстоянии.

Среднеквадратичная ошибка функции ковариации в исследуемых точках определяется по формуле

RMS = \sqrt{\frac{\sum_{i = 1}^{m} d_{i}^{2}}{m}},

где d_i – отклонение измеряемой и интерполированной величины в i-й точке измерения; m – количество точек измерений.

В исследовании используется набор данных о скорости подвижек земной коры 38 ГНСС-станций на севере Вьетнама. Выбор в пользу этих станций сделан на основе следующих статистических данных:

скорость подвижек земной коры в системе ITRF2000 на 22 ГНСС-станциях, которые задействованы при изучении системы разломов Красной реки, разломов Дьен Бьен Фу и реки Сон Да;
скорость подвижек земной коры в системе ITRF2005 на четырех ГНСС-станциях во Вьетнаме, которые являются частью Азиатско-Тихоокеанской сети (PCGIAP);
скорость подвижек земной коры в системе ITRF2005 одной станции DGNSS/CORS, работающей в военной системе координат;
скорость подвижек земной коры в системе ITRF2008 на 11 ГНСС-станциях, являющихся частью проекта Министерства природных ресурсов и окружающей среды Вьетнама, направленного на создание сейсмической геодезической сети в районах разломов на севере Вьетнама для прогноза стихийных бедствий.

Результаты

Построение модели абсолютных скоростей подвижек земной коры состоит из следующих этапов.

Этап 1 – унификация скоростей подвижек земной коры в системе координат ITRF2020. Для построения модели скорости подвижек разных ГНСС-станций в различных системах координат, представленных в табл.1, скорости подвижек должны быть приведены к одной системе координат. Пересчитанные значения представлены в табл.2.

Таблица 1

Координаты и скорость подвижек ГНСС-станций в северной области Вьетнама

Станция	φ, град	λ, град	V_E, мм/год	V_N, мм/год	V_U, мм/год	Система координат
CAM1	20,999	107,313	34,60	–13,41	32,95	ITRF2000
SOC1	21,308	105,826	32,88	–11,94	–1,84	ITRF2000
XUY0	21,849	105,738	34,95	–12,46	0,53	ITRF2000
TAM2	21,455	105,638	32,42	–12,24	–0,60	ITRF2000
BAV1	21,097	105,373	32,14	–11,08	–1,28	ITRF2000
OAN0	21,853	105,336	33,49	–11,85	–14,02	ITRF2000
HUN1	21,361	105,330	33,14	–11,69	–5,24	ITRF2000
DOI0	21,677	105,202	33,66	–11,83	–10,47	ITRF2000
NTH0	21,475	105,186	33,27	–12,23	–10,70	ITRF2000
SON1	21,191	105,181	32,80	–12,13	–3,73	ITRF2000
HOA1	20,864	105,178	33,90	–11,34	–2,75	ITRF2000
LAP1	21,384	105,033	32,92	–12,47	–4,99	ITRF2000
NAM0	21,691	104,458	35,09	–12,04	3,23	ITRF2000
MON1	21,189	104,245	32,43	–13,44	–1,05	ITRF2000
NOI1	21,131	104,172	33,03	–12,08	–4,40	ITRF2000
NAD2	20,984	104,167	32,36	–12,13	–10,19	ITRF2000
LOT1	21,203	104,064	33,45	–13,56	–6,17	ITRF2000
QTA2	21,306	103,943	33,91	–12,52	–9,63	ITRF2000
NGA1	22,268	103,242	39,12	–9,74	12,09	ITRF2000
HAM1	21,931	103,236	32,87	–10,47	15,33	ITRF2000
DON1	22,131	103,051	35,17	–12,10	15,17	ITRF2000
LEM1	21,792	103,029	34,83	–11,12	11,92	ITRF2000
DIEB	21,428	103,005	26,98	–9,60	3,92	ITRF2005
DOSN	20,694	106,795	27,35	–7,99	16,64	ITRF2005
NT01	20,668	106,814	36,00	–11,72	7,54	ITRF2005
QT01	21,403	103,029	29,92	–10,32	–19,98	ITRF2005
MCRS	21,526	107,968	30,80	–7,80	–1,80	ITRF2005
C004	21,926	103,238	37,58	–12,34	–14,60	ITRF2008
C014	20,147	105,136	35,94	–11,75	–9,85	ITRF2008
C022	21,029	104,312	30,04	–10,72	–7,04	ITRF2008
C033	21,549	104,036	34,70	–10,05	–15,56	ITRF2008
C045	21,119	104,982	31,79	–9,92	–29,24	ITRF2008
C049	22,225	104,445	39,34	–12,15	–26,71	ITRF2008
C052	21,636	104,787	34,08	–13,86	–30,45	ITRF2008
C056	20,880	105,497	31,55	–11,38	15,31	ITRF2008
C065	21,810	105,438	36,46	–13,50	–18,32	ITRF2008
C070	21,930	106,794	31,40	–12,91	8,97	ITRF2008
C075	20,988	106,816	34,68	–13,68	7,82	ITRF2008

Таблица 2

Скорости подвижек ГНСС-станций в системе координат ITRF2020

Станция	V_E, мм/год	V_N, мм/год	V_U, мм/год	V, мм/год	Az, град
CAM1	34,70	–11,83	32,89	36,66	108,8
SOC1	32,98	–10,36	–1,90	34,57	107,4
XUY0	35,05	–10,89	0,49	36,70	107,3
TAM2	32,52	–10,67	–0,65	34,22	108,2
BAV1	32,24	–9,50	–1,34	33,61	106,4
OAN0	33,59	–10,28	–14,06	35,12	107,0
HUN1	33,24	–10,11	–5,30	34,74	106,9
DOI0	33,76	–10,26	–10,52	35,28	106,9
NTH0	33,37	–10,66	–10,75	35,03	107,7
SON1	32,90	–10,55	–3,79	34,55	107,8
HOA1	34,00	–9,72	–2,99	35,36	106,0
LAP1	33,02	–10,89	–5,05	34,77	108,3
NAM0	35,19	–10,47	3,18	36,71	106,6
MON1	32,53	–11,86	–1,11	34,62	110,0
NOI1	33,13	–10,50	–4,47	34,75	107,6
NAD2	32,46	–10,55	–10,26	34,13	108,0
LOT1	33,55	–11,98	–6,23	35,62	109,7
QTA2	34,01	–10,94	–9,69	35,72	107,8
NGA1	39,22	–8,17	12,05	40,06	101,8
HAM1	32,97	–8,90	15,28	34,15	105,1
DON1	35,27	–10,53	15,13	36,81	106,6
LEM1	34,93	–9,55	11,87	36,21	105,3
DIEB	27,25	–9,75	3,85	28,94	109,7
DOSN	27,61	–8,15	16,58	28,79	106,4
NT01	36,26	–11,87	7,49	38,15	108,1
QT01	30,18	–10,47	–20,06	31,95	109,1
MCRS	31,00	–7,93	–1,89	32,00	104,3
C004	37,55	–12,47	–14,74	39,57	108,4
C014	35,92	–11,88	–9,98	37,83	108,3
C022	30,01	–10,84	–7,18	31,91	109,9
C033	34,68	–10,18	–15,69	36,14	106,4
C045	31,76	–10,05	–29,37	33,31	107,6
C049	39,31	–12,28	–26,85	41,18	107,3
C052	34,05	–13,99	–30,58	36,81	112,3
C056	31,53	–11,51	15,17	33,56	110,1
C065	36,43	–13,63	–18,46	38,90	110,5
C070	31,37	–13,04	8,83	33,98	112,6
C075	34,65	–13,81	7,69	37,30	111,7

Расчеты (табл.2) показывают, что значения горизонтальных смещений и азимута однородны, направление векторов движения северо-запад – юго-восток (рис.1). Это обязательное условие для расчета экспериментальной ковариации на разных расстояниях для использования метода наименьших квадратов.

Этап 2 – оценка скоростей V и азимута Az. Данные табл.2 показывают, что некоторые станции, данные о скорости движения которых отличаются от общего тренда станций в экспериментальном районе, должны быть оценены до использования их значений в построении модели скорости подвижек земной коры.

Средняя скорость и средний азимут ГНСС-станции определяются по формуле (1):

\begin{matrix} V_{a v} = \sum_{i = 1}^{38} V_{i} / 38 = 35,26 мм/год; \\ A z_{a v} = \sum_{i = 1}^{38} A z_{i} / 38 = 107,9 град . \end{matrix}

Поправочные числа v_i, v_^azi для i-й точки значений скорости и азимута определены по формуле (2) и представлены в табл.3.

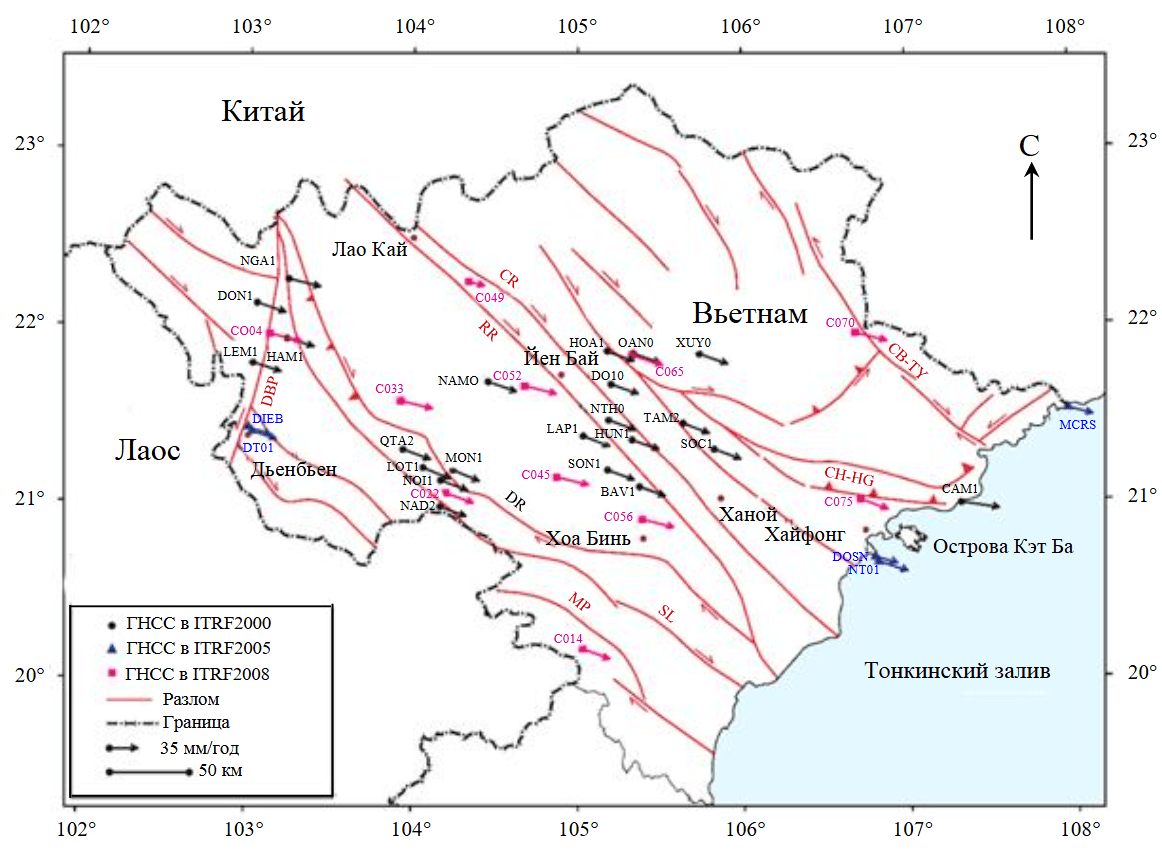
Рис.1. Карта скоростей подвижек земной коры на ГНСС-станциях севера Вьетнама в системе координат ITRF2020 (ГНСС-станции расположены на геологически стабильных позициях вблизи зон разломов)

Таблица 3

Отклонения скорости подвижек и азимута на станциях от соответствующих им средних значений

Станция	v_i, мм/год	v_{^azi ,}град	Станция	v_i, мм/год	v_^azi,град
CAM1	–1,40	–0,9	HAM1	1,11	2,8
SOC1	0,69	0,5	DON1	–1,55	1,3
XUY0	–1,44	0,6	LEM1	–0,95	2,6
TAM2	1,04	–0,3	DIEB	6,32	–1,8
BAV1	1,65	1,5	DOSN	6,47	1,5
OAN0	0,14	0,9	NT01	–2,89	–0,2
HUN1	0,52	1,0	QT01	3,31	–1,2
DOI0	–0,02	1,0	MCRS	3,26	3,6
NTH0	0,23	0,2	C004	–4,31	–0,5
SON1	0,71	0,1	C014	–2,57	–0,4
HOA1	–0,10	1,9	C022	3,35	–2,0
LAP1	0,49	–0,4	C033	–0,88	1,5
NAM0	–1,45	1,3	C045	1,95	0,3
MON1	0,64	–2,1	C049	–5,92	0,6
NOI1	0,51	0,3	C052	–1,55	–4,4
NAD2	1,13	–0,1	C056	1,70	–2,2
LOT1	–0,36	–1,8	C065	–3,64	–2,6
QTA2	–0,46	0,1	C070	1,28	–4,7
NGA1	–4,80	6,1	C075	–2,04	–3,8

Стандартные отклонения наблюдаемых значений определяются по формуле (3):

\begin{matrix} σ_{V} = \sqrt{\sum_{i = 1}^{38} v_{i}^{2} / 37} = \pm 2,62 мм/год; \\ σ_{A z} = \sqrt{\sum_{i = 1}^{38} v_{A z_{i}}^{2} / 37} = \pm 2,1 град . \end{matrix}

Таким образом, вероятность наблюдения скорости подвижек земной коры на ГНСС-станциях находятся в диапазонах (35,26 – 3σ) и (35,26 + 3σ) со значениями от 27,40 до 43,12 мм/год, а их направление движения на ГНСС-станциях в диапазонах (107,9 – 3σ) и (107,9 + 3σ) со значениями от 101,6 до 114,2 град равно 99,73 %. При дальнейшей обработке данных скорости подвижек, выходящие за пределы диапазона, не будут приниматься к расчету.

Результаты анализа показывают, что все станции находятся в указанном диапазоне, поэтому данные с этих станций использованы в дальнейших расчетах.

Этап 3 – построение модели абсолютной скорости подвижек земной коры. Для экспериментальных расчетов использовались 38 ГНСС-станций исследуемой области. Среди них четыре станции (OAN0, LOT1, C075 и QT01) применялись не для построения модели, а для проверки ее модели. Моделирование скорости подвижек земной коры основано на методе наименьших квадратов по коллокации функции Маркова 3-го порядка. При обработке данных определены характерные параметры функции, модель скорости подвижек земной коры в северной области Вьетнама выражается через функцию Маркова 3-го порядка:

\begin{matrix} C_{S_{V}} = - 3,7513 e^{\frac{S}{4,2143}} (1 - \frac{S}{4,2143} + \frac{S^{2}}{53,2810}); (6) \\ C_{S_{A z}} = 10,7777 e^{- \frac{S}{3,1549}} (1 + \frac{S}{3,1549} + \frac{S^{2}}{29,86018}) . (7) \end{matrix}

Стандартное отклонение между теоретической функцией ковариации и экспериментальной ковариацией скорости подвижек земной коры и азимута их направления определено по формуле (5) и составляет ±0,44 мм² и ±0,9 град² соответственно. Графики, представленные на рис.2, показывают, что величины скорости подвижек и азимута направления, определенные по теоретической ковариации, совпадают с экспериментальной ковариацией.

Значения скорости подвижек на тестируемых станциях интерполированы. Сопоставление этих величин с соответствующими им значениями (см. табл.2) представлено в табл.4.

В табл.4 показаны отклонения на контрольных станциях. Наивысшее отклонение составляет 1,94 мм/год, наименьшее – 0,17 мм/год. Эти значения сравнительно малы по отношению к средним скоростям подвижек земной коры, равным в исследуемом регионе ~35 мм/год.

Результаты, представленные в табл.4, показывают небольшое отклонение между значениями измеренных и интерполированных азимутов.

Таблица 4

Значения скорости и азимутов подвижек земной коры на проверенных ГНСС-станциях

Станция	Скорость подвижек, мм/год			Азимут подвижек, град
Станция	V	V_m^*	Отклонение	Az	Az_m^*	Отклонение
OAN0	35,12	35,29	–0,17	107,0	107,5	–0,5
LOT1	35,62	35,41	0,21	109,7	108,7	1,0
C075	37,30	35,36	1,94	111,7	109,8	1,9
QT01	31,95	31,20	0,75	109,1	108,5	0,6

^* Скорость и азимут подвижек земной коры, рассчитанные по модели.

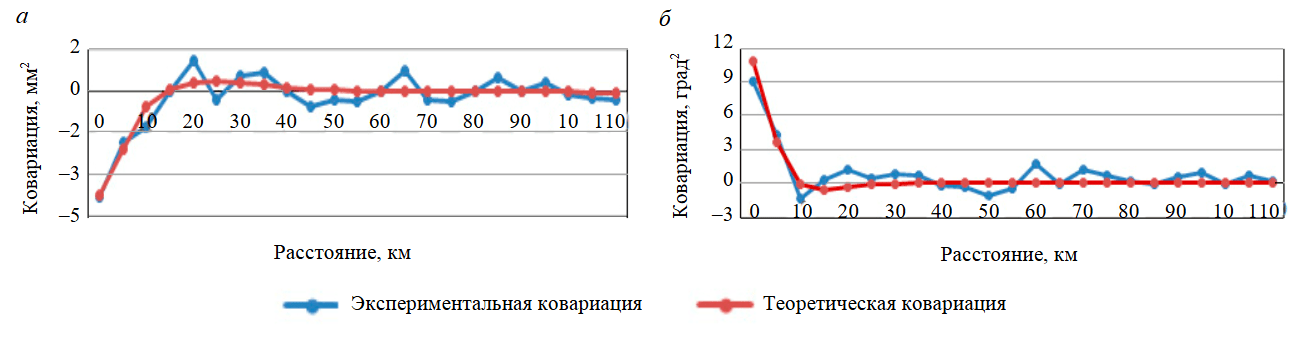
Рис.2. График функции Маркова 3-го порядка по скорости (а) и направлению (б) подвижек земной коры

Исходя из значений табл.4, среднеквадратичное отклонение скорости подвижек земной коры и азимута на проверенных станциях составляет ±1,05 мм/год и ±1,1 град соответственно. Это означает, что модель скорости подвижек земной коры и их азимут установлены для севера Вьетнама с использованием функции Маркова 3-го порядка, которое описано формулами (6) и (7).

Обсуждение

Север Вьетнама имеет сложную тектоническую структуру с преобладанием активных разломов, таких как разлом Красной реки, разлом реки Чай, разлом реки Ло, принадлежащих системе разломов Красной реки; разлом Дьен Бьен Фу, разлом реки Да и разлом Сон Ля. Разлом Красной реки играет важнейшую роль в этом регионе поскольку разделяет исследуемую область на две тектонические структуры – северо-западную и северо-восточную. Ранее подвижки земной коры на севере Вьетнама измерялись с использованием GPS-станций [16, 36], результаты мониторинга Вьетнама и прилегающих территорий показали подвижки этих станций в направлении с северо-запада к юго-востоку [16, 31]. Снижение скорости подвижек с запада на восток на северных GPS-станциях (Ланг, Бач Лонг Ви и Хай Нам) указывает на то, что область Тонкинского залива в данный момент сдавлена в субширотном направлении, т.е. направлении восток – юго-восток. Это поле напряжений неблагоприятно для активной системы разломов в субмеридиональном направлении наряду с разломами, простирающимися в направлении северо-запад – юго-восток.

В 2013 г. скорость подвижек земной коры в районе разлома Красной реки, определяемая с использованием анализа данных GPS, составляла 34,5 ± 1 мм/год на востоке 12 ± 1 мм/год на юге. Эти данные были получены с 27 станций на севере Вьетнама между 1994 и 2007 годами с использованием программного обеспечения GAMIT/GLOBK [30]. В то же время в 2001-2012 гг. скорость горизонтальных смещений на 22 GPS-станциях на северо-востоке Вьетнама, которые работают в системе ITRF2008, была определена с использованием программного обеспечения Bernese версии 5.0, скорость горизонтальных подвижек составила 34,3 ± 0,7 мм/год [16].

В 2016 г. абсолютные подвижки в южной части разлома Красной реки (Вьет Три – Ханой) были определены с использованием данных со станций Тхак Ба, Там Дао – Ба Ви наряду с измерениями, внесенными в 2013 и 2015 гг. Данный анализ был выполнен с использованием программного обеспечения Bernese 5.0, и средняя величина подвижек составила 34 мм/год [17].

В 2020 г. скорость подвижек земной коры на шести станциях (MTEV, MLAY, DBIV, TGIV, SMAV, SLAV) в северо-западной части Вьетнама, вместе со станцией PHUT в Ханое была определена с использованием GAMIT/GLOBK [36]. Значения скорости подвижек земной коры составили 34,10 ± 0,71 мм/год (DBIV), 34,31 ± 0,65 мм/год (PHUT), 34,51 ± 0,75 мм/год (SMAV), 34,55 ± 0,80 мм/год (MLAY), 34,80 ± 0,72 мм/год (TGIV), 34,93 ± 0,99 мм/год (SLAV), 35,59 ± 0,73 мм/год (MTEV). Эти значения соответствуют тектонической картине в Юго-Восточной Азии, которая движется на юго-восток из-за столкновения тектонических плит Индийского субконтинента с Евразийской плитой.

В 2022 г. станции, входящие в сеть VNGEONET, были выделены по их абсолютной скорости подвижек земной коры с использованием программного обеспечения GAMIT/GLOBK. Эти станции склонны двигаться в юго-восточном направлении с абсолютной скоростью: MCAI = 34,42 мм/год, SDON = 36,09 мм/год, HYEN = 32,87 мм/год, CPHU = 32,98 мм/год, TQUA = 33,95 мм/год и MGTE = 34,46 мм/год [37].

В данном исследовании подвижки земной коры на ГНСС-станциях севера Вьетнама были скорректированы с использованием метода наименьших квадратов и функции Маркова 3-го порядка, что позволило достичь точности около 2 мм/год в системе координат ITRF2020 для скорости подвижек и 2 град для азимута подвижек. Обработка данных в единой системе координат позволила сформировать целостную картину движения земной коры внутри общей сети. Скорость подвижек земной коры составила ~35 мм/год в направлении с северо-запада на юго-восток, что совпадало с предшествующими исследованиями в этом же регионе, тем самым подтвердилась точность корректировки данных из систем координат ITRF2000, ITRF2005, ITRF2008 в ITRF2020.

Заключение

Исследование посвящено преобразованию данных о скорости подвижек земной коры с 38 ГНСС-станций в различных динамических системах координат – ITRF2000, ITRF2005, ITRF2008 – в единую систему координат ITRF2020. Это преобразование достигнуто с использованием параметров, предоставленных ITRF.

Анализ показал, что скорость подвижек станций составляет ~35 мм/год преимущественно в направлении с северо-запада на юго-восток. Из всех станций 34 использованы для построения модели смещения земной коры, остальные четыре (OAN0, LOT1, C075 и QT01) – для проверки точности измерений и тестирования модели. Исследование включало применение метода коллокации наименьших квадратов для создания модели подвижек земной коры на севере Вьетнама.

Впервые построена модель подвижек земной коры на севере Вьетнама с использованием последней версии динамической системы координат, которая показала высокий уровень точности с отклонением не более 2 мм/год. Методология, включающая создание точной модели, несет в себе потенциал применения в других исследованиях с аналогичным набором данных. Это достижение имеет большое значение для понимания и практического применения знаний о подвижках земной коры. Результаты данного исследования служат ключевым источником данных, способствующих созданию и использованию динамической системы координат во Вьетнаме.

Литература

Altamimi Z., Rebischung P., Métivier L., Collilieux X. ITRF2014: A new release of the International Terrestrial Reference Frame modeling nonlinear station motions // Journal of Geophysical Research: Solid Earth. 2016. Vol. 121. Iss. 8. P. 6109-6131. DOI: 10.1002/2016JB013098
Amagua C.G.P., Euriques J.F., Alves S. da C., Krueger C.P. Analysis of local surface displacement using repeated GPS measurements: a case study of the Guabirotuba area, Curitiba, Brazil // Bulletin of Geodetic Sciences. 2022. Vol. 28. Iss. 1. № e2022005. DOI: 10.1590/s1982-21702022000100005
Araszkiewicz A. Integration of Distributed Dense Polish GNSS Data for Monitoring the Low Deformation Rates of Earth’s Crust // Remote Sensing. 2023. Vol. 15. Iss. 6. № 1504. DOI: 10.3390/rs15061504
Bevis M., Bedford J., Caccamise II D.J. The Art and Science of Trajectory Modelling / Geodetic Time Series Analysis in Earth Sciences // Springer. 2020. P. 1-27. DOI: 10.1007/978-3-030-21718-1_1
Bilgen B., Inal C. An open-source software for geodetic deformation analysis in GNSS networks // Earth Science Informatics. 2022. Vol. 15. Iss. 3. P. 2051-2062. DOI: 10.1007/s12145-022-00844-1
Bui T.H.T. Transformation coordinates between international terrestrial reference frames // Journal of Mining and Earth Sciences. 2013. Vol. 41. № 1. P. 53-57 (in Vietnamese).
Bui T.H.T. Research on the theoretic basis for the modernization of the national geodetic control network in Vietnam by global navigation satellite system GNSS: Specialty Geodesy and Mapping Ph.D. thesis, Hanoi University of Mining and Geology, Hanoi, Vietnam (2014). 142 p.
Bui T.H.T. Determination of absolute crustal movements of Việt Nam territory from data of Differential Global Navigation Satellite System (DGNSS) // Journal of Geology. Series A. 2014. Vol. 340 (1-2). P. 46-52.
Butwong K., Thongtan T., Boonterm K. Precision coordinate transformations for Thai national geodetic infrastructure // 20th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), 9-12 May 2023, Nakhon Phanom, Thailand. IEEE, 2023. 4 p. DOI: 10.1109/ECTI-CON58255.2023.10153290
Gang Chen, Anmin Zeng, Feng Ming, Yifan Jing. Multi-quadric collocation model of horizontal crustal movement // Solid Earth. 2015. Vol. 7. Iss. 3. P. 817-825. DOI: 10.5194/se-7-817-2016
Pengfei Cheng, Yingyan Cheng, Xiaoming Wang, Yantian Xu. Update China geodetic coordinate frame considering plate motion // Satellite Navigation. 2021. Vol. 2. № 2. DOI: 10.1186/s43020-020-00032-w
Gill J., Shariff N.S., Omar K., Amin Z.M. Tectonic motion of Malaysia: analysis from years 2001 to 2013 // ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences: Joint International Geoinformation Conference, 28-30 October 2015, Kuala Lumpur, Malaysia. Copernicus Publications, 2015. Vol. II-2/W2. P. 199-206. DOI: 10.5194/isprsannals-II-2-W2-199-2015
Guohua Gu, Wuxing Wang. Advantages of GNSS in Monitoring Crustal Deformation for Detection of Precursors to Strong Earthquakes // Positioning. 2013. Vol. 4. № 1. P. 11-19. DOI: 10.4236/pos.2013.41003
Häkli P., Evers K., Jivall L. et al. NKG2020 transformation: An updated transformation between dynamic and static reference frames in the Nordic and Baltic countries // Journal of Geodetic Science. 2023. Vol. 13. Iss. 1. № 20220155. DOI: 10.1515/jogs-2022-0155
Hodgkinson K.M., Mencin D.J., Feaux K. et al. Evaluation of Earthquake Magnitude Estimation and Event Detection Thresholds for Real‐Time GNSS Networks: Examples from Recent Events Captured by the Network of the Americas // Seismological Research Letters. 2020. Vol. 91. № 3. P. 1628-1645. DOI: 10.1785/0220190269
Jagoda M., Rutkowska M. An Analysis of the Eurasian Tectonic Plate Motion Parameters Based on GNSS Stations Positions in ITRF2014 // Sensors. 2020. Vol. 20. Iss. 21. № 6065. DOI: 10.3390/s20216065
Maciuk K., Szombara S. Annual crustal deformation based on GNSS observations between 1996 and 2016 // Arabian Journal of Geosciences. 2018. Vol. 11. Iss. 21. № 667. DOI: 10.1007/s12517-018-4022-4
Kuncoro H., Meilano I., Susilo S. Sunda and Sumatra Block Motion in ITRF2008 // International Symposium on Global Navigation Satellite System 2018, 21-23 November 2018, Bali, Indonesia. E3S Web of Conferences. 2019. Vol. 94. № 04006. DOI: 10.1051/e3sconf/20199404006
Minh L.H., Masson R.., Bourdillon A. et al. Recent crustal motion in Vietnam and in the Southeast Asia region by continuous GPS data // Vietnam Journal of Earth Sciences. 2014. Vol. 36. № 1. P. 1-13 (in Vietnamese). DOI: 10.15625/0866-7187/36/1/4132
Minh L.H., Hung V.T., Hu J.-C. et al. Contemporary movement of the Earth’s crust in the Northwestern Vietnam by continuous GPS data // Vietnam Journal of Earth Sciences. 2020. Vol. 42. № 4. P. 334-350. DOI: 10.15625/0866-7187/42/4/15282
Azhari M., Altamimi Z., Azman G. et al. Semi-kinematic geodetic reference frame based on the ITRF2014 for Malaysia // Journal of Geodetic Science. 2020. Vol. 10. Iss. 1. P. 91-109. DOI: 10.1515/jogs-2020-0108
Mattioli G., Mencin D., Hodgkinson K. et al. The EarthScope Plate Boundary Observatory and allied networks, the makings of nascent Earthquake and Tsunami Early Warning System in Western North America // European Geosciences Union General Assembly, 23-28 April 2017, Vienna, Austria. Geophysical Research Abstracts. 2016. Vol. 18. № EGU2016-10953.
Duong N., Sagiya T., Kimata F. et al. Contemporary horizontal crustal movement estimation for northwestern Vietnam inferred from repeated GPS measurements // Earth, Planets and Space. 2013. Vol. 65. Iss. 12. P. 1399-1410. DOI: 10.5047/eps.2013.09.010
Trọng N.G., Nghĩa N.V., Khải P.C. et al. Determination of tectonic velocities in Vietnam territory based on data of CORS stations of VNGEONET network // Journal of Hydro-Meteorology. 2022. Vol. 739. P. 59-66 (in Vietnamese). DOI: 10.36335/VNJHM.2022(739).59-66
Ohta Y., Ohzono M. Potential for crustal deformation monitoring using a dense cell phone carrier Global Navigation Satellite System network // Earth, Planets and Space. 2022. Vol. 74. Iss. 1. № 25. DOI: 10.1186/s40623-022-01585-7
Wei Qu, Hailu Chen, Shichuan Liang et al. Adaptive Least-Squares Collocation Algorithm Considering Distance Scale Factor for GPS Crustal Velocity Field Fitting and Estimation // Remote Sensing. 2019. Vol. 11. Iss. 22. № 2692. DOI: 10.3390/rs11222692
Rabah M., Shaker A., Farhan M. Towards a Semi-Kinematic Datum for Egypt // Positioning. 2015. Vol. 6. № 3. P. 49-60. DOI: 10.4236/pos.2015.63006
Rudenko S., Esselborn S., Schöne T., Dettmering D. Impact of terrestrial reference frame realizations on altimetry satellite orbit quality and global and regional sea level trends: a switch from ITRF2008 to ITRF2014 // Solid Earth. 2019. Vol. 10. Iss. 1. P. 293-305. DOI: 10.5194/se-10-293-2019
Steffen R., Legrand J., Ågren J. et al. HV-LSC-ex2: velocity field interpolation using extended least-squares collocation // Journal of Geodesy. 2022. Vol. 96. Iss. 3. № 15. DOI: 10.1007/s00190-022-01601-4
Tamay J., Galindo-Zaldivar J., Soto J., Gil A.J. GNSS Constraints to Active Tectonic Deformations of the South American Continental Margin in Ecuador // Sensors. 2021. Vol. 21. Iss. 12. № 4003. DOI: 10.3390/s21124003
Tran D.T., Nguyen Q.L., Nguyen D.H. General Geometric Model of GNSS Position Time Series for Crustal Deformation Studies – A Case Study of CORS Stations in Vietnam // Journal of the Polish Mineral Engineering Society. 2021. Vol. 1. № 2. P. 183-198. DOI: 10.29227/IM-2021-02-16
Trần Đ.T., Nguyễn T.Y., Dương C.C. et al. Recent crustal movements of northern Vietnam from GPS data // Journal of Geodynamics. 2013. Vol. 69. P. 5-10. DOI: 10.1016/j.jog.2012.02.009
Tucikešić S., Milinković A., Božić B. et al. GNSS Time Series as a Tool for Seismic Activity Analysis Related to Infrastructure Utilities // Contributions to International Conferences on Engineering Surveying. Cham: Springer, 2021. P. 246-256. DOI: 10.1007/978-3-030-51953-7_21
Hai V.Q., Cuong T.Q., Thuan N.V. Crustal movement along the Red River Fault zone from GNSS data // Vietnam Journal of Earth Sciences. 2016. Vol. 38. № 1. P. 14-21 (in Vietnamese). DOI: 10.15625/0866-7187/38/1/7846
Wang Wei, Dang Ya-Min, Zhang Chuan-Yin et al. Monitoring crustal deformation and gravity change caused by the terrestrial water load in the three gorges area base on CORS network // Chinese Journal of Geophysics. 2017. Vol. 60. Iss. 2. P. 154-163. DOI: 10.1002/cjg2.30035
Jarmołowski W. A priori noise and regularization in least squares collocation of gravity anomalies // Geodesy and Cartography. 2013. Vol. 62. № 2. P. 199-216. DOI: 10.2478/geocart-2013-0013
Jarmołowski W., Bakuła M. Two covariance models in Least Squares Collocation (LSC) tested in interpolation of local topography // Contributions to Geophysics and Geodesy. 2013. Vol. 43. № 1. P. 1-19. DOI: 10.2478/congeo-2013-0001

Модель движения земной коры в ITRF2020 – исследование на примере Северного Вьетнама

Аннотация

Введение

Методология

Результаты

Координаты и скорость подвижек ГНСС-станций в северной области Вьетнама

Скорости подвижек ГНСС-станций в системе координат ITRF2020

Отклонения скорости подвижек и азимута на станциях от соответствующих им средних значений

Значения скорости и азимутов подвижек земной коры на проверенных ГНСС-станциях

Обсуждение

Заключение

Литература

Похожие статьи