Моделирование распределения начального состава пластового флюида в газоконденсатной залежи с учетом рассеянных жидких углеводородов
- 1 — младший научный сотрудник Институт проблем нефти и газа РАН ▪ Orcid
- 2 — д-р техн. наук заместитель директора по научной работе Институт проблем нефти и газа РАН ▪ Orcid
- 3 — канд. физ.-мат. наук старший научный сотрудник Институт проблем нефти и газа РАН ▪ Orcid ▪ Scopus
- 4 — младший научный сотрудник Институт проблем нефти и газа РАН ▪ Orcid
- 5 — д-р техн. наук профессор Российский университет дружбы народов имени Патриса Лумумбы ▪ Orcid
Аннотация
В нефтегазовых пластах со значительным этажом продуктивности зависимость начального состава углеводородов от глубины – композиционный градиент – является важным фактором при оценке запасов компонентов, положения газонефтяного контакта, изменения свойств флюида по объему залежи. Известные модели композиционного градиента основываются на термодинамических соотношениях, предполагающих квазиравновесное состояние многокомпонентной гидродинамически связанной углеводородной системы в гравитационном поле с учетом влияния естественного геотермического градиента. Соответствующие алгоритмы позволяют рассчитывать изменение давления и состава углеводородного флюида с глубиной, включая определение положения газонефтяного контакта (ГНК). Выше и ниже ГНК состояние флюида считается однофазным. Для многих нефтегазоконденсатных залежей характерно присутствие в пределах газонасыщенной части пласта небольшой исходной доли жидкой углеводородной фазы (ЖУВ) – рассеянной нефти. Для учета данного явления предложена специальная модификация термодинамической модели и реализован алгоритм расчета композиционного градиента в газоконденсатной залежи с наличием ЖУВ. Рассмотрены примеры, моделирующие характерные составы и условия трех реальных нефтегазоконденсатных залежей. По результатам расчетов с использованием предложенного алгоритма показаны особенности изменения содержания ЖУВ и его влияния на распределение состава газоконденсатной смеси по глубине. Присутствие ЖУВ приводит к повышению уровня и возможному изменению типа флюидального контакта. Характер зависимости доли ЖУВ от глубины может быть различным и обусловлен растворением легких компонентов в насыщенной жидкой фазе. Состав ЖУВ в газоконденсатной части залежи изменяется с глубиной иначе, чем в нефтяной зоне, где жидкая фаза недонасыщена легкими углеводородами. Результаты работы имеют значение для оценки начальных запасов и потенциальной эффективности извлечения углеводородных компонентов в газоконденсатных и нефтегазоконденсатных залежах с большим этажом продуктивности.
Финансирование
Работа выполнена в рамках Государственного задания ИПНГ РАН по темам 122022800272-4 «Совершенствование методов моделирования, лабораторных и промысловых исследований для создания новых технологий эффективного экологически чистого извлечения углеводородов в сложных горно-геологических условиях» и 122022800274-8 «Создание научных основ новой системной методологии прогноза, поисков и освоения залежей углеводородов, включая залежи матричной нефти в газонасыщенных карбонатных отложениях нефтегазоконденсатных месторождений»
Введение
Оценка распределения начального компонентного состава пластового флюида в объеме продуктивного пласта – одна из ключевых задач при комплексном исследовании залежи, оценке запасов углеводородов и проектировании разработки. Фактическую информацию для анализа пространственного изменения состава и свойств углеводородов предоставляют исследования проб пластового флюида [1, 2], измерения характеристик потока пластоиспытателями [3, 4], испытания скважин и газоконденсатные исследования [5, 6], оптические методы [7]. Геохимические исследования [8, 9], биомаркеры [10, 11], групповой и изотопный анализ [12, 13] в комбинации с методами статистического анализа и кластеризации [14] и углубленным анализом динамики пластового давления по объектам разработки [15] позволяют установить различные источники поступления углеводородного флюида в залежь, а гидродинамические исследования скважин, гидропрослушивание, трассерные исследования, анализ флюидальных контактов – наличие гидродинамически несвязанных зон пласта [16-18].
Во многих залежах отмечается закономерное изменение состава флюида с глубиной. В большинстве случаев оно проявляется в увеличении плотности, снижении газосодержания и давления насыщения для нефти или в повышении содержания конденсата и давления начала конденсации для газоконденсатной системы [1, 2, 19]. Это явление принято называть «композиционный градиент» (градиент состава). Теоретические модели композиционного градиента, настроенные на фактические данные, используются для расчета начального содержания углеводородов в пласте, уточнения положения газонефтяных контактов, получения исходных данных для проектирования разработки залежи и инициализации математических моделей пласта [1, 20, 21]. Данные о вариациях состава и фазового состояния флюида позволяют оптимизировать режимы эксплуатации скважин и оборудование для добычи, оценить альтернативные варианты воздействия и агенты закачки с учетом зависимости свойств флюида и условий смесимости от глубины. В конечном итоге эти факторы могут существенно повлиять на стратегию разработки месторождения с экономической точки зрения [22, 23].
В случае нефтегазоконденсатных залежей существующие модели композиционного градиента позволяют рассчитывать изменения по глубине состава и давления в пределах газонасыщенных и нефтенасыщенных интервалов, а также оценивать положение газонефтяного контакта (ГНК). При этом не учитывается возможное наличие в газоконденсатной части залежи с начала разработки так называемой рассеянной нефти (жидких углеводородов – ЖУВ), подтвержденное для ряда крупных нефтегазоконденсатных месторождений.
В данной статье представлена модификация метода и алгоритма для расчета композиционного градиента с учетом наличия ЖУВ в газоконденсатной части залежи. Исследуются особенности изменения начального состава флюида и доли ЖУВ в газонасыщенном интервале на трех примерах, моделирующих условия реальных нефтегазоконденсатных залежей.
Методы
Теоретические модели композиционного градиента
Модели композиционного градиента можно разделить на изотермические и учитывающие естественный температурный (геотермический) градиент.
Соотношение для расчета изменения состава флюида под действием силы тяжести в изотермической системе было впервые получено Гиббсом [24]. Он показал, что для многокомпонентной изотермической системы в условиях равновесия в гравитационном поле соблюдается баланс между изменением химического и гравитационного потенциала с глубиной. Условие равновесия выражается соотношением
где μi – химический потенциал компонента iна глубине h; Mi – молярная масса компонента i; g – гравитационная постоянная (ускорение свободного падения); N – число компонентов в системе.
Интегрируя (1) и выражая химические потенциалы через летучести с использованием уравнения состояния, соотношение можно свести к системе алгебраических уравнений для последовательного определения значений давления и концентраций компонентов на разной глубине с шагом Δh [1]. Таким образом, движение вверх и вниз от опорной точки с заданными составом флюида и давлением позволяет рассчитать распределения давления и концентраций компонентов по вертикали. Описанная процедура применима для однофазного состояния пластовой углеводородной системы. Особенности, связанные с определением положения ГНК, обсуждаются далее.
Соотношение (1) предполагает, что система в целом находится при постоянной температуре (dT/dh = 0). Изотермическая модель применима к реальным залежам при небольших диапазонах глубин (этажах продуктивности) и градиентах пластовой температуры. В остальных случаях рекомендуется учитывать влияние геотермического градиента.
В естественном геотермальном поле вертикальный градиент температуры вызывает термодиффузионный эффект – дополнительную «тепловую силу», влияющую на распределение концентраций компонентов с глубиной. Для количественной оценки влияния термодиффузии используют модели, учитывающие гравитационный и термический факторы. Формируемое ими квазиравновесное распределение состава по глубине подчиняется следующему общему уравнению баланса [20]
где zi – мольная доля компонента; h – глубина; Fig и – FiT гравитационная сила сегрегации и тепловая сила для i-го компонента соответственно.
Основным фактором, контролирующим изменение состава с глубиной, обычно является гравитационная сила. Термодиффузия, как правило, действует против силы тяжести и ослабляет ее влияние на проявление композиционного градиента. В большинстве залежей порядок влияния тепловой силы меньше, чем гравитационной [20, 25].
Одна из наиболее теоретически обоснованных и удобных для практического применения моделей для тепловой силы была предложена Хаазе [26, 27]. В этой модели тепловая сила может быть получена через предельное значение термодиффузионных коэффициентов при стремящемся к нулю градиенте температуры и принимает вид:
где Mi, Hi – молекулярная масса и парциальная мольная энтальпия компонента i; M и H – молекулярная масса и мольная энтальпия смеси.
Опираясь на модель Хаазе, Педерсен и Линделеф получили следующее соотношение для расчета композиционного градиента [19, 21, 28]:
где p – давление; z¯ – вектор мольных концентраций компонентов в смеси (мольный состав смеси); T1 и T2, h1 и h2 – значения температуры и глубины для первой и второй рассматриваемых точек соответственно; R – универсальная газовая постоянная; fi – летучесть компонента i.
Зависимость летучестей от давления и состава смеси определяется через решение кубического уравнения состояния, например, уравнения Пенга – Робинсона. Система уравнений (2) решается на каждом шаге по глубине относительно давления и состава флюида в точке h2 при известных значениях на глубине h1. Подробности расчета энтальпии представлены в [19, 29].
Практическая реализация модели композиционного градиента
В данной работе для реализации модели композиционного градиента (задачи композиционного профилирования) используется консервативная разностная схема [30]. Для решения получаемой системы нелинейных алгебраических уравнений применяется метод Ньютона, обеспечивающий эффективное решение задач композиционного профилирования при использовании решения предыдущего шага в качестве начального приближения [1, 2]. Последовательный поиск значений базовых неизвестных осуществляется на каждой итерации решением системы линейных уравнений AY = b методом исключения Гаусса, выбор которого обусловлен заполненной структурой матрицы и типичной размерностью в несколько десятков уравнений:
где индекс m соответствует текущей, m– 1 – предыдущей итерации; ψi – невязка уравнения (2) на предыдущей итерации для компонента i (с обратным знаком); Δ – изменение базовой неизвестной на текущей итерации. В качестве начального приближения на первой итерации используются значения на глубине h1.
Таким образом, если состав и давление известны на опорной глубине, то их можно последовательно определить для любой другой заданной глубины на основе системы (2). При этом значения температуры на каждой глубине считаются известными в соответствии с заданным геотермическим градиентом. Входными параметрами модели являются параметры уравнения состояния и удельные энтальпии компонентов. Для чистых веществ они являются справочными данными, а для псевдокомпонентов и фракций определяются на основе представленных в литературе корреляций и решения задач идентификации по фактическим измерениям при исследовании проб пластового флюида.
Описанная модель применима для однофазного состояния системы. Классический расчет композиционного градиента предполагает, что смесь достигает насыщения и переходит в двухфазное состояние на глубине ГНК. Для проверки фазового состояния смеси используется специальная итерационная процедура – тест стабильности Михельсена [31]. Стабильность, полученная в результате этого теста, означает однофазное состояние смеси, нестабильность – двухфазное состояние, соответствующее переходу через ГНК. Таким образом, для поиска ГНК на каждой глубине при полученном давлении и составе проверяется стабильность смеси. Если смесь на очередном шаге стала нестабильной, для точного определения положения ГНК на соответствующем промежутке глубин реализуется алгоритм деления пополам [32].
На глубине ГНК давление совпадает с давлением начала конденсации для газовой фазы (при подходе сверху) и давлением насыщения для жидкой фазы (при подходе снизу). Поэтому альтернативный метод поиска ГНК предполагает на каждом шаге по глубине расчет давления перехода смеси в двухфазное состояние [33]. После того, как положение ГНК найдено, необходимо перейти от состава газовой к составу равновесной жидкой фазы, или наоборот. Для этого решается задача фазового равновесия [1, 2].
Отмеченные особенности справедливы для классического (насыщенного) ГНК. В глубокопогруженных залежах при высоких давлениях и температурах переход от газовой к жидкой фазе может быть сверхкритическим. В этом случае двухфазное состояние в пределах залежи не возникает, но на отметке ГНК однофазный флюид меняет тип фазового состояния с газового на жидкое. На ГНК для смеси достигается максимум давления насыщения/начала конденсации, но он ниже, чем давление на отметке ГНК.
Важно отметить отличия термодинамических расчетов композиционного градиента от принципов, используемых при равновесной инициализации гидродинамических моделей нефтегазовых залежей. В гидродинамическом моделировании не учитываются эффекты термодиффузии, тогда как классические расчеты композиционного градиента не учитывают наличие капиллярной переходной зоны «газ – нефть». Сосуществование газовой и жидкой углеводородных фаз предполагается только на поверхности ГНК.
Переходная зона «газ – нефть» обычно ограничена единицами, реже первыми десятками метров, что связано с большей разницей плотностей фаз и меньшими значениями поверхностного натяжения, чем для системы «нефть – вода». Тогда как эффект композиционного градиента проявляет себя на больших диапазонах глубин, измеряемых сотнями метров. При этом влияние капиллярного давления на фазовые равновесия «газ – нефть» даже в плотных коллекторах не является значительным [1, 22] и оказывает заметный эффект только для сланцевых залежей. Таким образом, предполагается, что пренебрежение влиянием капиллярного давления и наличием двухфазной переходной зоны «газ – нефть» не оказывает существенного влияния на расчет распределения начального состава углеводородов по глубине. В данной работе авторы также следуют указанному подходу и не учитывают наличие капиллярной переходной зоны «газ – нефть». Возможность преодоления соответствующего ограничения обсуждается в заключении.
Композиционный градиент при наличии рассеянной жидкой углеводородной фазы
В газоконденсатных залежах часто отмечается наличие в порах небольшого объема неподвижных ЖУВ, в разных источниках называемых рассеянной, реликтовой, остаточной или матричной нефтью [1, 34]. В этом случае описанный выше классический расчет квазиравновесного начального распределения флюида не применим, так как он предполагает сосуществование двух фаз только на ГНК [22].
Впервые наличие такого типа флюида в газоконденсатной части залежи было установлено для Оренбургского нефтегазоконденсатного месторождения (НГКМ) как по керну, так и по особенностям фазового поведения флюида [1, 35]. Наличие ЖУВ в газонасыщенных интервалах подтверждено для основной залежи Вуктыльского НГКМ [34] и, вероятно, характерно для других НГКМ [22]. В отличие от конденсата, ЖУВ присутствуют в газонасыщенной зоне пласта с начала разработки и отличаются более тяжелым составом, включая смолы и асфальтены. Присутствие ЖУВ отмечается во всем интервале глубин газонасыщенной зоны, а не только в относительно небольшой капиллярной переходной зоне вблизи ГНК. Насыщенность рассеянных ЖУВ обычно оценивается в 5-15 %.
В работах [34, 35] предложено следующее объяснение данного явления. Термины «матричная нефть» и «ЖУВ» в таком контексте соответствуют парадигме о нефтегазоматеринских свойствах продуктивных карбонатных отложений, слагающих газоконденсатные и нефтегазоконденсатные месторождения, в частности, Вуктыльское и Оренбургское. В результате предыдущих исследований показано наличие в поровом пространстве карбонатных пород газовой части этих месторождений собственной (матричной) нефти, преобразованной до жидких углеводородов нефтяного ряда (ЖУВ). Установленные нефтегазоматеринские свойства и ранние стадии нефтегенерации продуктивных отложений позволяют утверждать, что еще до начала разработки в их газовой части ЖУВ находятся в состоянии термодинамического равновесия с газом, но при насыщенностях ниже порога фильтрации. Именно такие ЖУВ и рассматриваются в данной работе.
Для учета ЖУВ в газоконденсатной части залежи в работе [36] был предложен модифицированный алгоритм композиционного градиента. Он предполагает, что газовая фаза непрерывно связана по глубине и ее состав соответствует квазиравновесным условиям (2). Жидкая фаза неподвижна и не связана между глубинами, поэтому квазиравновесные условия для жидкой фазы не выполняются. При этом на каждой глубине жидкая фаза равновесна соответствующему составу газовой фазы.
Как и в классическом расчете, в качестве исходных данных для модифицированного алгоритма задаются состав флюида на опорной глубине, давление, температура и геотермальный градиент. Из-за наличия ЖУВ общий состав флюида на опорной глубине должен соответствовать двухфазному состоянию с долей жидкой углеводородной фазы, оцененной по результатам геофизических исследований скважин и лабораторным исследованиям керна. Для этого полученный по пробам состав газоконденсатного флюида предварительно донасыщается до соответствующего значения мольной доли ЖУВ L0 [22].
Подобная процедура донасыщения необходима по следующей причине. Из-за наличия ЖУВ в газоконденсатной части залежи любое изменение пластового давления в окрестности скважины переводит систему в двухфазное состояние, связанное не только с выпадением конденсата, но и с дегазацией насыщенной нефти (ЖУВ). Это приводит к некоторому искажению состава флюида при стандартных методиках газоконденсатных исследований. В результате проба флюида может оказываться недонасыщенной, что не позволяет использовать ее состав в качестве состава пластовой газоконденсатной смеси при наличии ЖУВ. Например, в случае Вуктыльского НГКМ отмечается расхождение между пластовым давлением и давлением начала конденсации от 20 до 40 бар с нарастанием по глубине [34].
Таким образом, в отличие от классического композиционного градиента, в алгоритме с ЖУВ входной состав на опорной глубине задается нестабильным. Это контролируется с помощью теста стабильности Михельсена [31]. Следующим шагом является определение соответствующих равновесных составов газовой (паровой) и жидкой фаз, а также расчетной доли ЖУВ с помощью решения задачи фазового равновесия [2]. Расчетная доля ЖУВ должна соответствовать величине L0. Полученный состав газовой фазы y ¯ 0 является насыщенным и далее используется в качестве входного состава смеси z ¯ 0 для расчета композиционного градиента вверх и вниз от опорной точки.
При движении вниз по глубине состав газоконденсатной смеси утяжеляется. Насыщенная на предыдущем шаге газовая фаза в новой точке становится перенасыщенной, т.е. превращается в двухфазную смесь z ¯ 1 . Для этой смеси при давлении и температуре на новой глубине определяются равновесные составы газовой фазы y ¯ 1 , жидкой фазы x ¯ 1 и их доли Vh = 1 – Lh и Lh. Полученная газовая фаза y ¯ 1 вновь является предельно насыщенной.
При движении вверх состав газоконденсатной смеси становится легче (беднее), поэтому смесь z ¯ 1 становится недонасыщенной. Для нее может быть рассчитан псевдоравновесный состав жидкой фазы x ¯ 1 с помощью процедуры Negative Flash, предложенной Витсоном и Михельсеном [37].
Negative Flash расширяет обычный алгоритм фазового равновесия за пределы двухфазной области, чтобы проводить вычисления в условиях, когда флюид является однофазным. Значение мольной доли газовой фазы 0 < Vh < 1 как при обычном расчете фазового равновесия, так и при Negative Flash подразумевает, что Vh молей газа найденного состава y ¯ 1 необходимо добавить к 1 – Vh молям жидкости найденного состава для восстановления исходного состава смеси . Аналогично Vh > 1 (недонасыщенный газ) при процедуре Negative Flash интерпретируется так, что Vh - 1 молей жидкости состава x ¯ 1 должны быть удалены из Vh молей газа состава y ¯ 1 для восстановления одного моля исходной смеси z ¯ 1 .
Таким образом, в обоих случаях (шаги вверх и вниз) полученный по итогам процедуры Negative Flash предельно насыщенный состав газовой фазы принимается в качестве итогового состава газоконденсатной смеси на новой глубине, а состав жидкой фазы – в качестве равновесного состава ЖУВ на этой глубине. Доля ЖУВ корректируется по сравнению со значением на предыдущей глубине, учитывая дополнительную конденсацию из газоконденсатной смеси при перенасыщении (шаг вниз) или, наоборот, испарение при недонасыщении (шаг вверх):
где Li – итоговая доля ЖУВ на новой глубине; Lh – доля ЖУВ, полученная из процедуры Negative Flash.
В процессе движения вниз по глубине в алгоритме с учетом ЖУВ отслеживается достижение отметки ГНК при L1 = 1 (переход к однофазному жидкому состоянию). При движении вверх контролируется возможный переход к однофазному газовому состоянию (L1 = 0). В обоих случаях дальнейшие шаги осуществляются с использованием классического (однофазного) расчета композиционного градиента.
Общая блок-схема алгоритма с учетом ЖУВ представлена на рис.1.
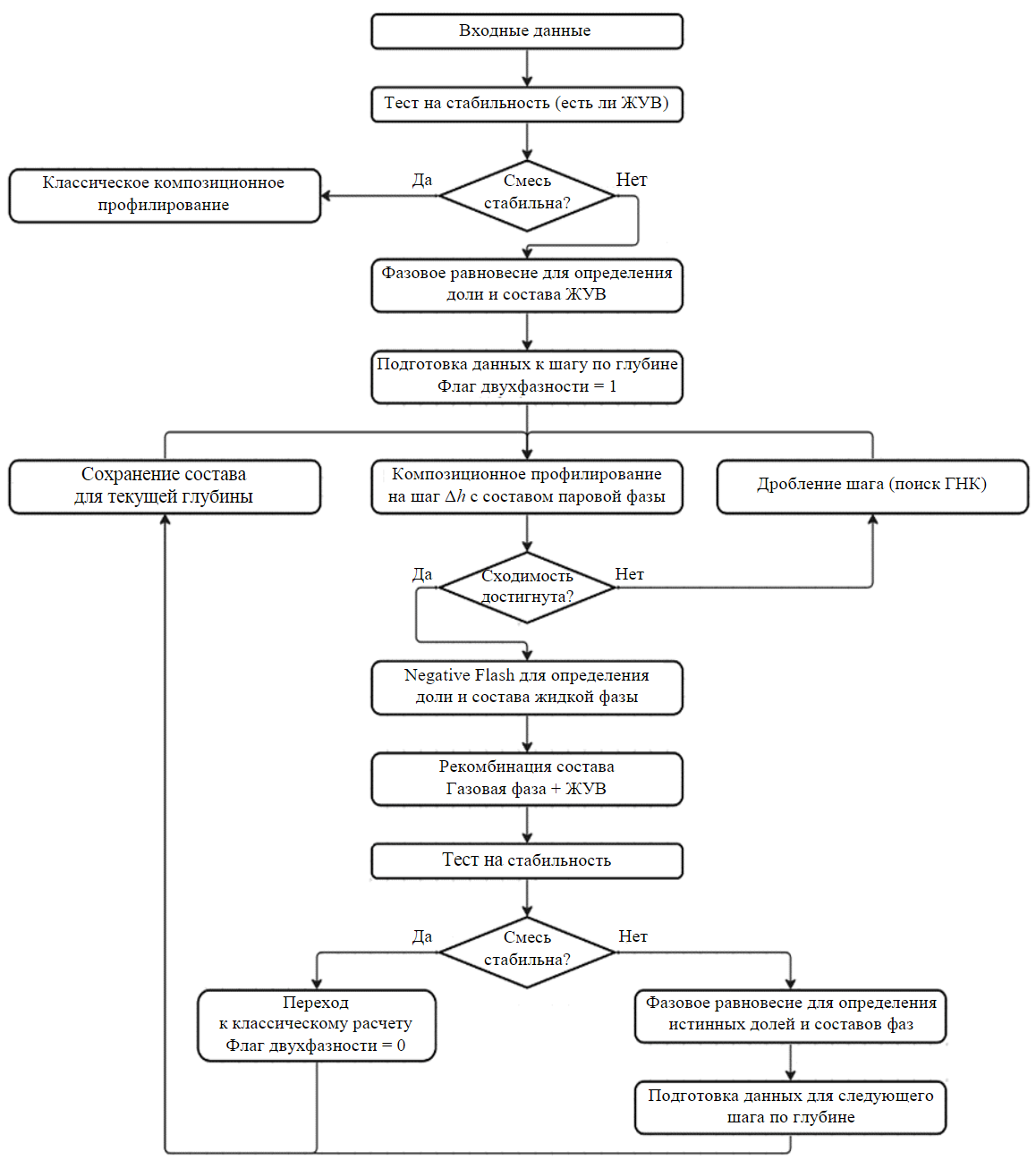
Рис.1. Блок-схема алгоритма композиционного профилирования с учетом ЖУВ
Обсуждение результатов
Оценка влияния ЖУВ на распределение состава в газоконденсатных залежах
Описанные алгоритмы композиционного профилирования использованы для расчетной оценки влияния ЖУВ на распределение давления и состава в газоконденсатных залежах. Параметры многокомпонентных моделей флюида, пластовые условия и исходные данные на опорной глубине принимались близкими к характеристикам трех различных газоконденсатных объектов: одной из ачимовских залежей Уренгойского НГКМ, основной залежи Оренбургского НГКМ и основной залежи Вуктыльского НГКМ.
По данным исследования керна продуктивные карбонатные нефтегазоматеринские породы крупных НГКМ (Вуктыльского и Оренбургского) до начала разработки дифобны [35], т.е. проявляют фобность по отношению к воде и немного менее – к жидким углеводородам, с углом смачивания 110-120°. С учетом большой этажности рассматриваемых залежей, это является дополнительным фактором, чтобы считать размер переходной зоны и влияние капиллярных сил несущественными для данной работы.
Выполненные расчеты не учитывают всей специфики соответствующих объектов и исследуют особенности влияния ЖУВ только в рамках предположений используемой модели. Например, для Оренбургского НГКМ прямые исследования показали наличие в пласте существенной доли тяжелых битумоидов (тяжелых смол и асфальтенов) [35]. В рассматриваемой постановке задачи их наличие и взаимодействие с моделируемым пластовым флюидом не учитывается, несмотря на высокую адсорбционную способность по отношению к легким углеводородным компонентам. Кроме того, повышенные концентрации тяжелых битумоидов из-за нефтематеринских свойств карбонатных пород Оренбургского НГКМ, как правило, связаны с низкопроницаемыми гидрофильными разностями с высокими значениями капиллярного давления «газ – вода», что может оказывать эффект своеобразного «затвора» для газовой фазы. Оценка влияния этих и других дополнительных факторов выходит за рамки текущей стадии исследований.
Состав 1 близок к условиям одной из ачимовских залежей Уренгойского НГКМ с уникальным содержанием конденсата в пластовом газе. Пластовый флюид моделируется смесью из 24 компонентов (табл.1). Опорная глубина h = 3754,6 м, давление на опорной глубине р = 633 бар, температура Т = 107,85 °С, геотермический градиент dT = 0,029 °С/м. Состав соответствует пробе газоконденсатного флюида на этой глубине. Расчет выполнен в диапазоне глубин от 3614 до 4050 м с шагом 1 м.
Таблица 1
Исходные данные для состава 1
|
Компоненты |
Мольная доля z, % |
Молярная масса M, г/моль |
Критическая температура Tc, °С |
Критическое давление pc, бар |
Ацентрический фактор ω |
Мольная энтальпия*Href, Дж |
Коэффициенты для кубической аппроксимации теплоемкости идеального газа**[38] |
|||
|
A |
B |
C |
D |
|||||||
|
N2 |
0,247 |
28,013 |
–146,95 |
33,9439 |
0,04 |
8330,789 |
31,1488 |
-0,0136 |
0,0 |
0,0 |
|
CO2 |
0,631 |
44,01 |
31,55 |
73,8659 |
0,225 |
19459,1011 |
19,7946 |
0,0734 |
–0,0001 |
0,0 |
|
C1 |
75,2122 |
16,043 |
–82,55 |
46,0421 |
0,013 |
2,6425 |
19,2503 |
0,0521 |
0,0 |
0,0 |
|
C2 |
7,2009 |
30,07 |
32,28 |
48,8387 |
0,0986 |
9761,1347 |
5,4092 |
0,1781 |
–0,0001 |
0,0 |
|
C3 |
4,394 |
44,097 |
96,65 |
42,4552 |
0,1524 |
19519,6224 |
–4,2244 |
0,3063 |
–0,0002 |
0,0 |
|
iC4 |
0,953 |
58,124 |
134,95 |
36,477 |
0,1848 |
29278,1232 |
–1,39 |
0,3847 |
–0,0002 |
0,0 |
|
nC4 |
1,514 |
58,124 |
152,05 |
37,9665 |
0,201 |
29278,1212 |
9,487 |
0,3313 |
–0,0001 |
0,0 |
|
iC5 |
0,537 |
72,151 |
187,25 |
33,8932 |
0,227 |
39036,6099 |
–9,5247 |
0,5066 |
–0,0003 |
0,0 |
|
nC5 |
0,565 |
72,151 |
196,45 |
33,7007 |
0,251 |
39036,6099 |
–3,6257 |
0,4873 |
–0,0003 |
0,0 |
|
C6 |
0,772 |
78,93 |
245,97 |
34,7 |
0,243 |
48795,1026 |
–4,4128 |
0,5819 |
–0,0003 |
0,0 |
|
C7 |
1,16 |
91,8 |
265,95 |
32,5 |
0,292 |
52706,294 |
–5,7687 |
0,5393 |
–0,0002 |
0,0 |
|
C8 |
1,33 |
103,35 |
295,077 |
29,928 |
0,34 |
60741,5508 |
–4,0418 |
0,5889 |
–0,0002 |
0,0 |
|
C9 |
0,801 |
119,17 |
322,415 |
27,987 |
0,388 |
71747,4235 |
–3,2364 |
0,6745 |
–0,0003 |
0,0 |
|
C10 |
0,698 |
133,0 |
346,673 |
26,238 |
0,435 |
81368,8653 |
–0,7145 |
0,7468 |
–0,0003 |
0,0 |
|
C11+ |
0,853 |
153,1083 |
377,537 |
24,1149 |
0,4991 |
63652,7132 |
27,5423 |
0,9068 |
–0,0004 |
0,0 |
|
C13+ |
0,659 |
180,4253 |
415,592 |
21,9509 |
0,5828 |
75009,3798 |
32,4562 |
1,0686 |
–0,0004 |
0,0 |
|
C15+ |
0,542 |
206,7519 |
447,928 |
20,3132 |
0,6605 |
85954,3171 |
37,1921 |
1,2246 |
–0,0005 |
0,0 |
|
C17+ |
0,544 |
237,3727 |
479,571 |
18,6716 |
0,7466 |
98684,4935 |
42,7004 |
1,4059 |
–0,0005 |
0,0 |
|
C20+ |
0,386 |
273,544 |
511,485 |
17,0456 |
0,8454 |
113722,2268 |
49,2071 |
1,6202 |
–0,0006 |
0,0 |
|
C22+ |
0,278 |
308,9098 |
539,266 |
15,7848 |
0,9382 |
128425,0729 |
55,569 |
1,8296 |
–0,0007 |
0,0 |
|
C25+ |
0,206 |
341,7057 |
561,92 |
14,7838 |
1,0222 |
142059,533 |
61,4685 |
2,0239 |
–0,0008 |
0,0 |
|
C27+ |
0,152 |
373,5677 |
581,777 |
13,9428 |
1,1019 |
155305,7262 |
67,2001 |
2,2126 |
–0,0009 |
0,0 |
|
C30+ |
0,137 |
408,5766 |
601,806 |
13,1577 |
1,1878 |
169860,2063 |
73,4978 |
2,42 |
–0,0009 |
0,0 |
|
C36+ |
0,228 |
650,0 |
630,02 |
12,2 |
1,5 |
270228,725 |
116,9268 |
3,8499 |
–0,0015 |
0,0 |
* Парциальная мольная энтальпия в идеально газовом состоянии при температуре 273,15 K, Дж.
** Коэффициенты A, B, C, D используются в расчете энтальпии.
На рис.2 представлен результат работы классического алгоритма (без учета ЖУВ). Здесь и далее через ПС5+ обозначено потенциальное содержание компонентов группы C5+ в пластовой газоконденсатной смеси, характеризующее количество растворенных углеводородов, которые нормальных условиях находятся в жидком состоянии (конденсат) [1].
На рис.2 видно, что с глубиной давление и ПС5+ увеличиваются (рис.2, а, б), концентрация легких компонентов уменьшается (рис.2, в), тяжелых – увеличивается (рис.2, г, д).
Рассматриваемая газоконденсатная залежь отличается близостью пластовых условий к критическим. Поэтому на рис.2, а давление и давление насыщения в точке максимума (ГНК) не совпадают, а на кривой ПС5+ (рис.2, б) виден непрерывный сверхкритический переход от газовой к жидкой фазе.
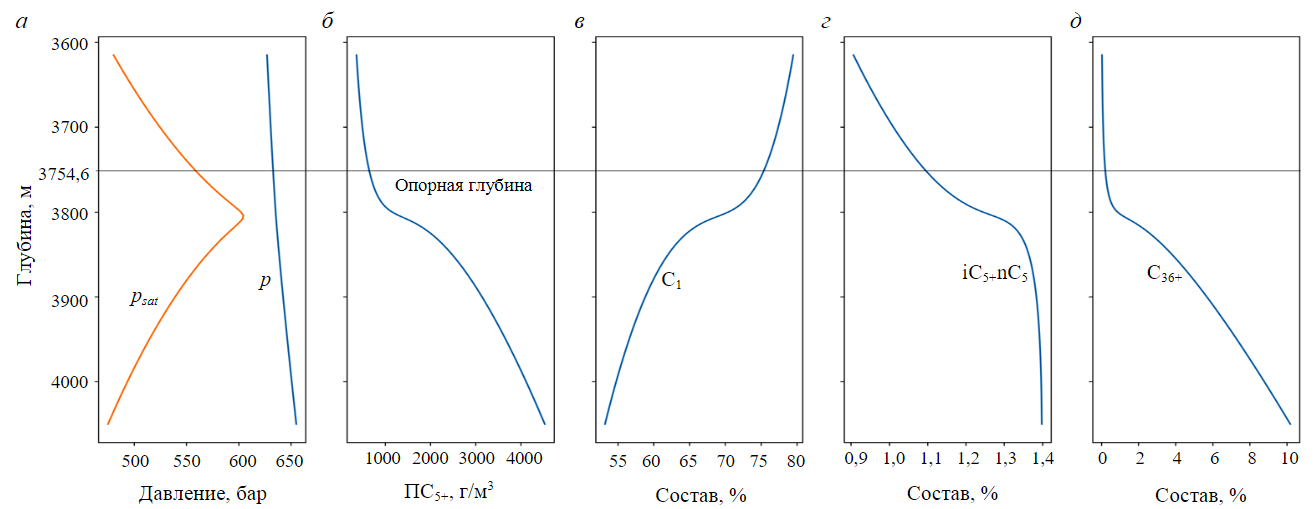
Рис.2. Результаты работы классического алгоритма для состава 1
Расчетные зависимости от глубины: а – давления p и давления насыщения psat, бар; б – ПС5+, г/м3; в – мольной доли метана, %; г – мольной доли пентанов, %; д – мольной доли группы C36+, %
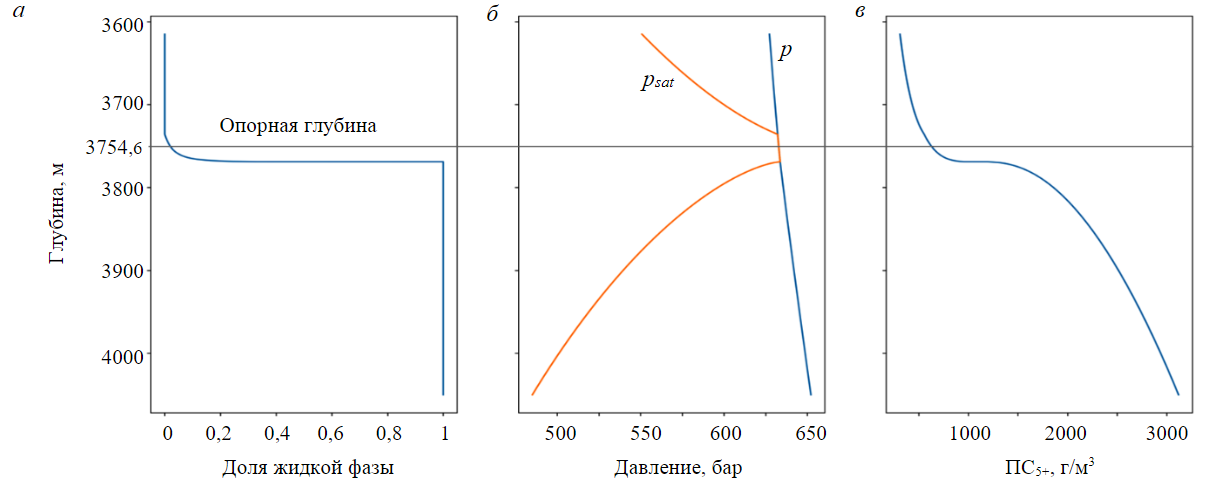
Рис.3. Результаты работы модифицированного алгоритма для состава 1
Расчетные зависимости от глубины: а – мольной доли жидкой фазы; б – давления p и давления насыщения psat, бар; в – ПС5+, г/м3
Чтобы продемонстрировать влияние ЖУВ на распределение компонентного состава, модифицируем состав смеси в опорной точке. К исходному составу из табл. 1 добавим псевдоравновесную жидкую фазу с составом, полученным из процедуры Negative Flash, до получения мольной доли ЖУВ 3% (L0 = 0,03). Результаты расчетов по модифицированному алгоритму композиционного профилирования (с учетом ЖУВ) представлены на рис.3.
Из рис.3, а видно, что при движении вверх от опорной глубины 3754,6 м доля ЖУВ ожидаемо уменьшается, а при движении вниз – увеличивается. Изменение доли ЖУВ от 0 до 1 происходит на интервале глубин от 3736 до 3769 м. На этом же интервале значения пластового давления и давления насыщения (начала конденсации) совпадают (рис.3, б), что свидетельствует о двухфазном состоянии системы: газовая фаза насыщена и присутствует жидкая фаза. Выше и ниже этого интервала графики на рис.3, б перестают совпадать, что свидетельствует о переходе в однофазную область. Выше отметки 3736 м газоконденсатная смесь становится недонасыщенной, ЖУВ отсутствуют. На отметке 3769 м отмечается ГНК, доля ЖУВ становится равной 100 %. Из сравнения рис.2 и 3 видно, что учет ЖУВ приводит к смене сверхкритического газонефтяного контакта на классический и увеличению значений ПС5+ (рис.3, в), т.е. росту содержания конденсата в пластовом газе.
Состав 2 по основным параметрам близок к условиям основной залежи Оренбургского НГКМ. Пластовый флюид моделируется смесью из 23 компонентов, включая 15 псевдофракций (табл.2). Опорная глубина h = 1250 м, давление на опорной глубине р = 195 бар, температура Т = 29,34 °С, геотермический градиент dT = 0,009 °С/м. В опорной точке выполнено донасыщение состава до мольной доли ЖУВ 8 % (L0 = 0,08).
Результаты работы модифицированного алгоритма приведены на рис.4.
Таблица 2
Исходные данные для состава 2
|
Компоненты |
Мольная доля z, % |
Молярная масса M, г/моль |
Критическая температура Tc, °С |
Критическое давление pc, бар |
Ацентрический фактор ω |
Мольная энтальпия Href, Дж |
Коэффициенты для кубической аппроксимации теплоемкости идеального газа [38] |
|||
|
A |
B |
C |
D |
|||||||
|
N2 |
5,4704 |
28,013 |
–146,95 |
33,944 |
0,04 |
8330,789 |
31,1488 |
-0,0136 |
0,0 |
0,0 |
|
CO2 |
0,6595 |
44,01 |
31,55 |
73,866 |
0,225 |
19459,1011 |
19,7946 |
0,0734 |
–0,0001 |
0,0 |
|
H2S |
1,7432 |
34,076 |
100,45 |
89,369 |
0,1 |
12550,8657 |
31,9401 |
0,0014 |
0,0 |
0,0 |
|
C1 |
83,2209 |
16,043 |
–82,55 |
46,042 |
0,013 |
2,6425 |
19,2503 |
0,0521 |
0,0 |
0,0 |
|
C2 |
4,0362 |
30,07 |
32,28 |
48,839 |
0,0986 |
9761,1347 |
5,4092 |
0,1781 |
–0,0001 |
0,0 |
|
C3 |
1,7471 |
44,097 |
96,65 |
42,455 |
0,1524 |
19519,6224 |
–4,2244 |
0,3063 |
–0,0002 |
0,0 |
|
IC4 |
0,3152 |
58,124 |
134,95 |
36,477 |
0,1848 |
29278,1212 |
–1,39 |
0,3847 |
–0,0002 |
0,0 |
|
C4 |
0,6338 |
58,124 |
146,35 |
37,47 |
0,1956 |
29278,1212 |
9,487 |
0,3313 |
–0,0001 |
0,0 |
|
F1 |
0,9559 |
84,0 |
226,5 |
30,7 |
0,2706 |
34921,866 |
15,1105 |
0,4975 |
–0,0002 |
0,0 |
|
F2 |
0,436 |
94,0 |
264,5 |
30,92 |
0,324 |
39079,231 |
16,9094 |
0,5568 |
–0,0002 |
0,0 |
|
F3 |
0,2809 |
110,0 |
301,1 |
29,07 |
0,3566 |
45731,015 |
19,7876 |
0,6515 |
–0,0003 |
0,0 |
|
F4 |
0,1706 |
126,0 |
333,7 |
27,04 |
0,4078 |
52382,799 |
22,6658 |
0,7463 |
–0,0003 |
0,0 |
|
F5 |
0,1005 |
141,0 |
364,0 |
25,37 |
0,4764 |
58618,8465 |
25,3641 |
0,8351 |
–0,0003 |
0,0 |
|
F6 |
0,051 |
156,0 |
395,2 |
24,28 |
0,5427 |
64854,894 |
28,0624 |
0,924 |
–0,0004 |
0,0 |
|
F7 |
0,0378 |
173,0 |
424,8 |
23,03 |
0,6141 |
71922,4145 |
31,1205 |
1,0247 |
–0,0004 |
0,0 |
|
F8 |
0,0383 |
203,0 |
456,2 |
20,93 |
0,6437 |
84394,5095 |
36,5171 |
1,2024 |
–0,0005 |
0,0 |
|
F9 |
0,0292 |
220,0 |
487,7 |
20,58 |
0,7118 |
91462,03 |
39,5752 |
1,303 |
–0,0005 |
0,0 |
|
F10 |
0,025 |
273,0 |
514,4 |
17,3 |
0,728 |
113496,0645 |
49,1093 |
1,617 |
–0,0006 |
0,0 |
|
F11 |
0,0115 |
296,0 |
539,1 |
16,46 |
0,8339 |
123058,004 |
53,2467 |
1,7532 |
–0,0007 |
0,0 |
|
F12 |
0,0104 |
310,0 |
562,9 |
16,13 |
0,976 |
128878,315 |
55,7651 |
1,8361 |
–0,0007 |
0,0 |
|
F13 |
0,0074 |
356,0 |
588,9 |
14,64 |
1,0396 |
148002,194 |
64,0399 |
2,1086 |
–0,0008 |
0,0 |
|
F14 |
0,0019 |
372,0 |
605,0 |
14,29 |
1,1295 |
154653,978 |
66,9181 |
2,2033 |
–0,0009 |
0,0 |
|
F15 |
0,0173 |
565,0 |
668,8 |
10,58 |
1,1534 |
234891,1225 |
101,6364 |
3,3464 |
–0,0013 |
0,0 |
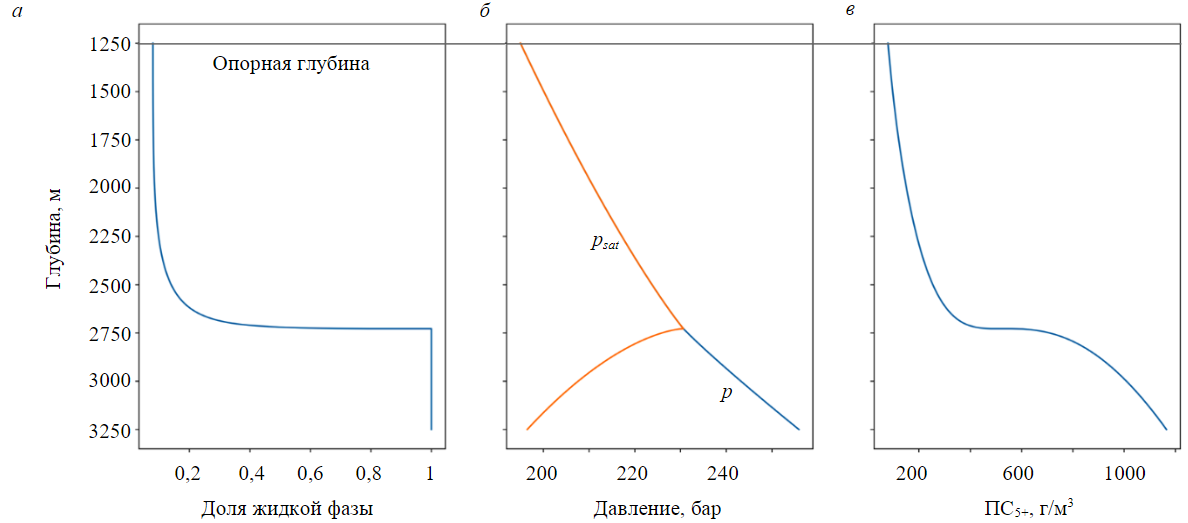
Рис.4. Результаты работы модифицированного алгоритма для состава 2
Расчетные зависимости от глубины: а – мольной доли жидкой фазы; б – давления p и давления насыщения psat, бар; в – ПС5+, г/м3
На глубинах до 2728 м давление насыщения (начала конденсации) и пластовое давление совпадают (рис.4, б), присутствует насыщенная газоконденсатная смесь и ЖУВ. Доля ЖУВ возрастает с глубиной и на отметке 2728 м достигает 100 %, наблюдается классический газонефтяной контакт (рис.4, а). Ниже ГНК значения пластового давления и давления насыщения перестают совпадать (рис.4, б), что соответствует однофазной области с недонасыщенной нефтью – нефтяной оторочке. Значения ПС5+ достаточно равномерно возрастают с глубиной в газоконденсатной области и более интенсивно – ниже ГНК (рис.4, в), что отражает характер роста содержания тяжелых компонентов.
Состав 3 моделирует условия, подобные основной залежи Вуктыльского НГКМ. Флюид представлен смесью из 19 компонентов (табл.3). Опорная глубина h = 3025 м, давление на опорной глубине р = 362,9 бар, температура Т = 61,4 °С, геотермический градиент dT = 0,0175 °С/м. В опорной точке выполнено донасыщение состава до мольной доли ЖУВ 14 % (L0 = 0,14).
Результаты работы модифицированного алгоритма представлены на рис.5.
Таблица 3
Исходные данные для состава 3
|
Компоненты |
Мольная доля z, % |
Молярная масса M, г/моль |
Критическая температура Tc, °С |
Критическое давление pc, бар |
Ацентрический фактор ω |
Мольная энтальпия Href, Дж |
Коэффициенты для кубической аппроксимации теплоемкости идеального газа [38] |
|||
|
A |
B |
C |
D |
|||||||
|
N2 |
4,8184 |
28,013 |
–146,8889 |
33,9912 |
0,045 |
8330,789 |
31,1488 |
–0,0136 |
0,0 |
0,0 |
|
CO2 |
0,0408 |
44,01 |
31,0556 |
73,8153 |
0,231 |
19459,1011 |
19,7946 |
0,0734 |
–0,0001 |
0,0 |
|
C1 |
72,8929 |
16,043 |
–82,5722 |
46,0432 |
0,0115 |
2,6425 |
19,2503 |
0,0521 |
0,0 |
0,0 |
|
C2 |
8,7255 |
30,07 |
32,2722 |
48,8011 |
0,0908 |
9761,1347 |
5,4092 |
0,1781 |
–0,0001 |
0,0 |
|
C3 |
3,5793 |
44,097 |
96,6722 |
42,4924 |
0,1454 |
19519,6224 |
–4,2244 |
0,3063 |
–0,0002 |
0,0 |
|
IC4 |
0,4663 |
58,124 |
134,9889 |
36,4802 |
0,1756 |
29278,1212 |
–1,39 |
0,3847 |
–0,0002 |
0,0 |
|
C4 |
0,8435 |
58,124 |
152,0278 |
37,9694 |
0,1928 |
29278,1212 |
9,487 |
0,3313 |
–0,0001 |
0,0 |
|
IC5 |
0,1743 |
72,151 |
187,2778 |
33,8119 |
0,2273 |
39036,6099 |
–9,5247 |
0,5066 |
–0,0003 |
0,0 |
|
C5 |
0,1409 |
72,151 |
196,5 |
33,6878 |
0,251 |
39036,6099 |
–3,6257 |
0,4873 |
–0,0003 |
0,0 |
|
C6P1 |
2,018 |
85,0188 |
250,9278 |
26,6887 |
0,1208 |
35345,4179 |
7,9027 |
0,5004 |
–0,0002 |
0,0 |
|
C6P2 |
3,138 |
110,457 |
318,9667 |
24,7149 |
0,2351 |
45921,0074 |
6,0966 |
0,6562 |
–0,0002 |
0,0 |
|
C6P3 |
1,815 |
157,953 |
398,0444 |
20,7256 |
0,3625 |
65666,8306 |
11,8058 |
0,9287 |
–0,0004 |
0,0 |
|
C6P4 |
0,5837 |
231,218 |
488,5167 |
16,8437 |
0,5589 |
96125,7653 |
22,824 |
1,3619 |
–0,0005 |
0,0 |
|
C6P5 |
0,299 |
338,184 |
586,3389 |
13,5525 |
0,7602 |
140595,426 |
42,4439 |
1,9968 |
–0,0008 |
0,0 |
|
C6P6 |
0,1931 |
500,0 |
679,6444 |
10,5933 |
1,0268 |
207868,25 |
75,7996 |
2,9481 |
–0,0011 |
0,0 |
|
C6P7 |
0,1216 |
598,0 |
674,6278 |
7,5153 |
1,3 |
248610,427 |
25,5721 |
3,407 |
–0,0014 |
0,0 |
|
C6P8 |
0,0778 |
794,1 |
737,6278 |
5,9157 |
1,481 |
330136,3547 |
33,1361 |
4,5271 |
–0,0018 |
0,0 |
|
C6P9 |
0,0475 |
1004,1 |
790,0722 |
4,8401 |
1,627 |
417441,0197 |
40,9978 |
5,7255 |
–0,0023 |
0,0 |
|
C6P10 |
0,0242 |
1284,2 |
845,0722 |
3,916 |
1,781 |
533888,7808 |
50,3553 |
7,3196 |
–0,0029 |
0,0 |
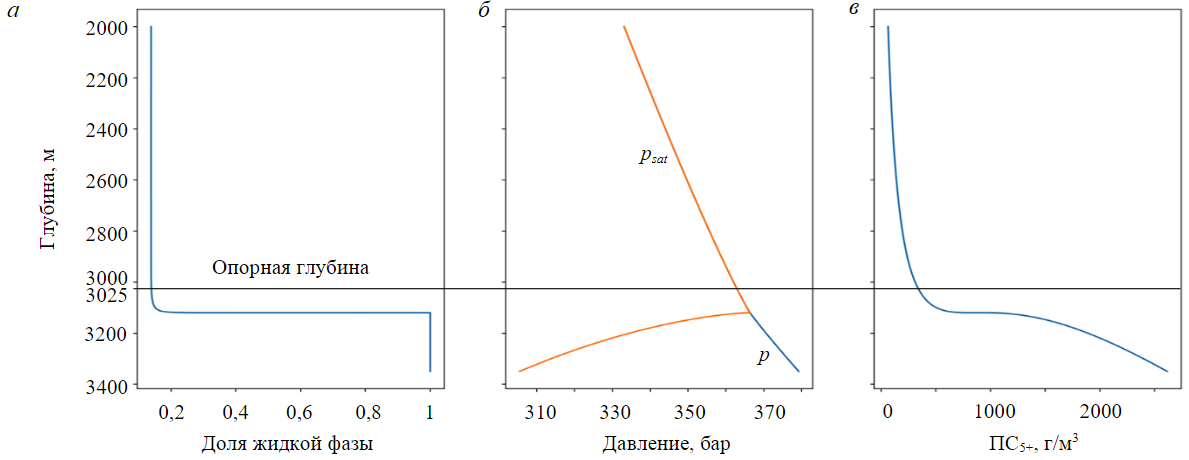
Рис.5. Результаты работы модифицированного алгоритма для состава 3
Расчетные зависимости от глубины: а – мольной доли жидкой фазы; б – давления p и давления насыщения psat, бар; в – ПС5+, г/м3
Для состава 3 изменение доли ЖУВ происходит на интервале глубин до 3120 м, где доля ЖУВ достигает 100 % и наблюдается классический ГНК (рис.5, а). Ниже значения пластового давления и давления насыщения перестают совпадать (рис.5, б), что соответствует однофазному недонасыщенному жидкому состоянию. Характер поведения кривой ПС5+ аналогичен составу 2, но с более интенсивным ростом ниже ГНК (рис.5, в).
Представляет интерес сопоставление результатов расчетов для составов 2 и 3 (рис.6). Здесь ось глубин относительная, за нулевую отметку принят уровень ГНК для каждой из залежей. Графики ПС5+ для составов 2 и 3 схожи почти во всем интервале глубин газоконденсатной области, кроме района ГНК. Здесь у состава 3 увеличение ПС5+ более плавное, чем у состава 2 (рис.6, б). При этом зависимости доли ЖУВ от глубины сильно различаются (рис.6, а). Для состава 2 доля ЖУВ плавно возрастает по всей глубине вплоть до ГНК. Для состава 3 существенное изменение доли ЖУВ отмечается только при приближении к уровню ГНК.
Для анализа отмеченных различий рассмотрим изменение по глубине доли отдельных компонентов в составе жидкой фазы, получаемое расчетом по процедуре Negative Flash. Графики долей компонентов от верхней границы расчетных глубин до уровня ГНК представлены на рис.7 для составов 2 и 3. Обратим внимание, что наибольший вклад в изменение доли ЖУВ вносит компонент С1 – метан (рис.7, а, е). Можно заметить, что для состава 2 изменение доли метана в жидкой фазе достаточно равномерно на протяжении всего расчетного интервала глубин, в то время как для состава 3 существенные изменения начинаются вблизи ГНК. Аналогичное поведение наблюдается и на графике изменения доли ЖУВ (рис.7, д, к).
Таким образом, характер изменения доли ЖУВ от глубины определяется эффектом набухания за счет растворения легких компонентов, в частности, метана с наибольшей концентрацией в жидкой фазе. Важно отметить, что состав ЖУВ в газоконденсатной части залежи изменяется с глубиной иначе, чем в нефтяной. С глубиной возрастает давление и доля промежуточных компонентов в газовой фазе и как следствие – в равновесной с ней жидкой фазе. С увеличением концентрации С3-С4 в насыщенной жидкой фазе возрастает растворимость метана. Эта тенденция противоположна утяжелению жидкой фазы, характерному для недонасыщенного состояния ниже уровня ГНК. Отметим, что заметное по рис.7 резкое снижение содержания промежуточных и некоторых тяжелых компонентов возле ГНК связано с ростом содержания метана и нормировкой концентраций.
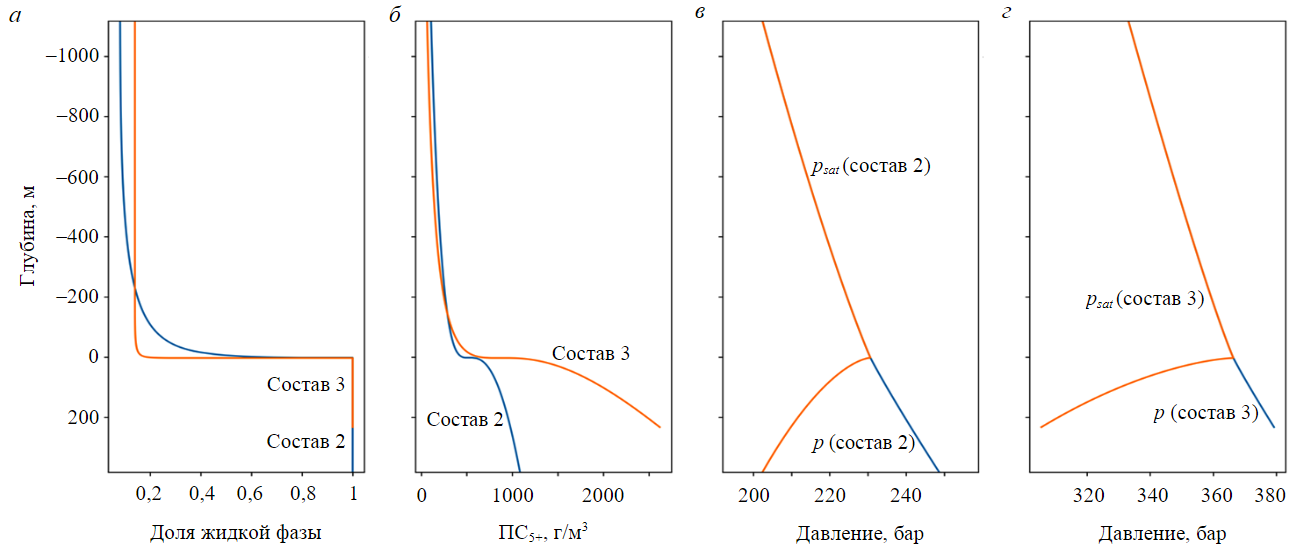
Рис.6. Сравнение результатов работы модифицированного алгоритма для составов 2 и 3
Расчетные зависимости от глубины: а – мольной доли жидкой фазы, для составов 2 и 3; б – ПС5+, г/м3, для составов 2 и 3; в – давления p и давления насыщения psat, бар, для состава 2; г – давления p и давления насыщения psat, бар, для состава 3
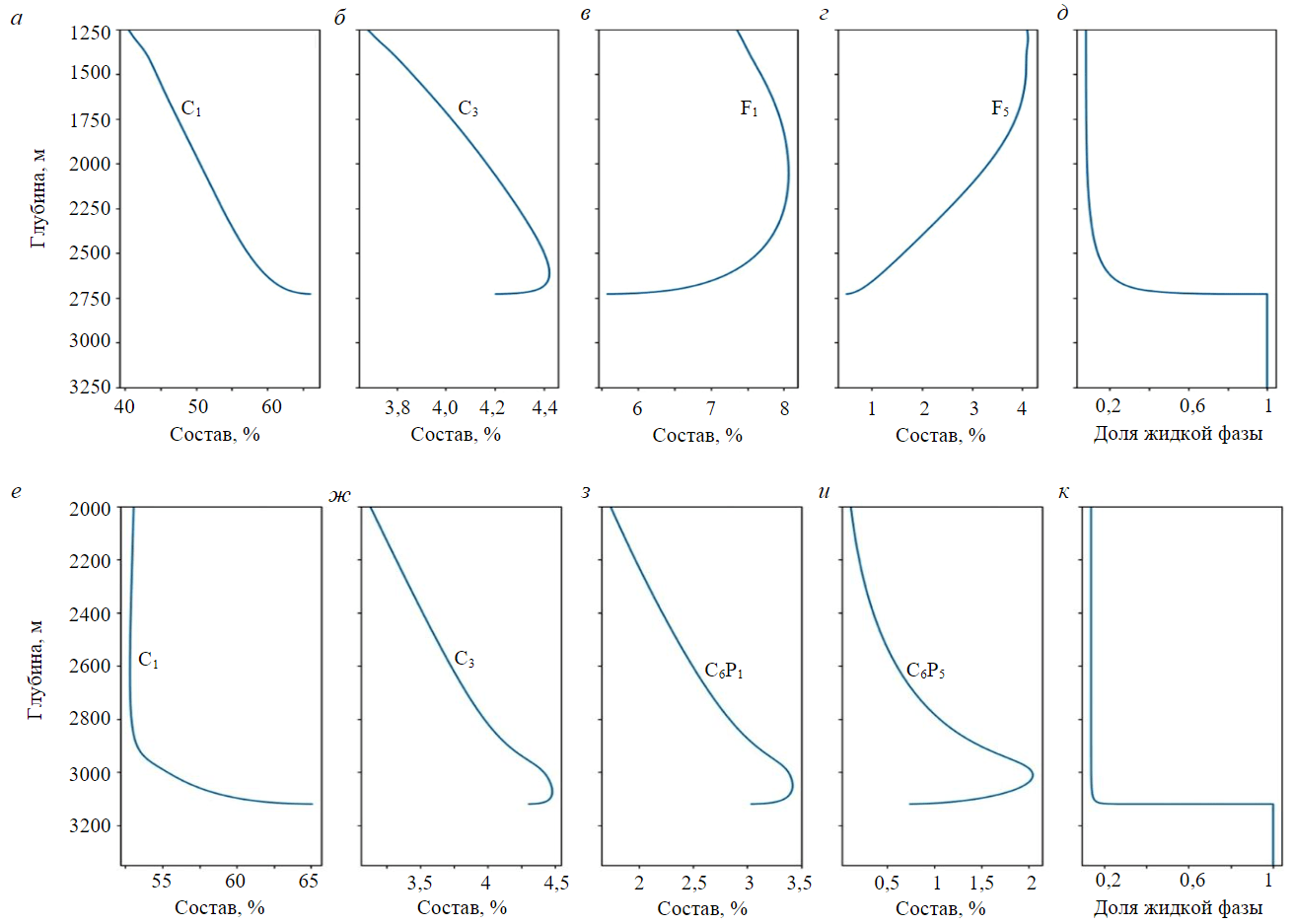
Рис.7. Изменение мольных концентраций компонентов в жидкой фазе для составов 2 и 3
Расчетные зависимости от глубины: а – мольной доли метана, %; б – мольной доли пропана, %; в – мольной доли фракции F1, %; г – мольной доли фракции F5, %; д – мольной доли жидкой фазы (состав 2); е – мольной доли метана, %; ж – мольной доли пропана, %; з – мольной доли фракции C6P1; и – мольной доли фракции C6P5, %; к – мольной доли жидкой фазы (состав 3)
Заключение
Отмечаемое для многих газоконденсатных залежей присутствие в пласте небольшой доли рассеянных ЖУВ требует изменения подходов к расчету начального распределения состава по глубине. При этом классические методы расчета композиционного градиента не применимы.
Рассмотренный и реализованный в статье модифицированный алгоритм композиционного профилирования позволяет не отказываться полностью от концепции квазиравновесного начального состояния углеводородной системы, но дополнить ее необходимыми предположениями и расчетными процедурами для согласованного учета рассеянных ЖУВ.
Представлены примеры расчетов для различных газоконденсатных смесей, близких по составу и условиям к реальным нефтегазоконденсатным залежам с большим этажом продуктивности. Они демонстрируют ряд характерных особенностей влияния ЖУВ на композиционный градиент: повышение уровня и возможное изменение типа флюидального контакта, а также зависимости ПС5+ от глубины. В зонах наличия ЖУВ пластовый газоконденсатный флюид является предельно насыщенным, давление начала конденсации совпадает с пластовым давлением.
Показано, что характер изменения доли ЖУВ с глубиной может быть различным. При этом наибольший вклад вносят легкие компоненты, что можно объяснить эффектом набухания насыщенной жидкой фазы. Изменение состава ЖУВ с глубиной в газоконденсатной части залежи также проявляет существенно иные тенденции, чем в нефтяной зоне, где жидкая фаза недонасыщена легкими углеводородами.
Предлагаемый подход к учету ЖУВ, а также концепция квазиравновесного композиционного градиента позволяют термодинамически согласованно рассчитывать начальное состояние нефтегазоконденсатных залежей с наличием рассеянных ЖУВ, оценивать положение ГНК и распределение по объему пласта запасов газа, жидких углеводородов и отдельных компонентов. Результаты расчета композиционного градиента с учетом ЖУВ определяют начальные условия при моделировании разработки месторождения и обосновании технологических решений по эффективному извлечению углеводородов.
Представленный метод опирается на предположения о псевдоравновесном распределении по глубине газовой фазы и локальном термодинамическом равновесии между газоконденсатным флюидом и рассеянными ЖУВ. Их применимость к условиям конкретных нефтегазоконденсатных залежей требует дальнейшего исследования с учетом особенностей формирования и накопленного фактического материала.
В анализ корректности вычисления композиционного градиента рекомендуется включать проверку расчетных концентраций компонентов группы С5+ в контрольных точках по глубине. Обычно ожидается, что они должны удовлетворять двухпараметрическому закону гамма-распределения [2]. Также для некоторых объектов отмечено, что фактическое изменение с глубиной концентраций компонентов С5+ носит преимущественно линейный характер [34].
В дальнейшем представленный метод может быть уточнен для учета капиллярного давления и переходной зоны «газ – нефть» по аналогии, например, с работой [39]. Текущая версия метода также прогнозирует формирование переходной зоны с ростом насыщенности ЖУВ до 100 % на ГНК (см. рис.3, а, 4, а, 5, а), но не за счет капиллярных эффектов, а на основе термодинамики.
Литература
- Брусиловский А.И. Фазовые превращения при разработке месторождений нефти и газа. М.: Грааль, 2002. 575 с.
- Whitson C.H., Brulé M.R. Phase behavior. Richardson: Society of Petroleum Engineers, 2000. Vol. 20. 240 p. DOI: 10.2118/9781555630874
- Novikov S., Weinheber P., Charupa M. et al. Tight Gas Achimov Formation Evaluation and Sampling with Wireline Logging Tools: Advanced Approaches and Technologies // SPE Russian Petroleum Technology Conference, 26-28 October 2015, Moscow, Russia. OnePetro, 2015. № SPE-176591-MS. DOI: 10.2118/176591-MS
- Gusev S., Garaev A., Zeybek M. et al. Reservoir Connectivity and Compartmentalization Detection with Down Hole Fluid Analysis Compositional Grading // SPE Russian Petroleum Technology Conference, 26-29 October 2020. OnePetro, 2020. № SPE-201895-MS. DOI: 10.2118/201895-MS
- Основы испытания пластов / Под ред. А.Г.Загуренко. М., Ижевск: Институт компьютерных исследований, 2012. 432 с.
- Алиев З.С., Исмагилов Р.Н. Газогидродинамические основы исследования скважин на газоконденсатность. М.: Недра, 2012. 214 с.
- Raupov I., Burkhanov R., Lutfullin A. et al. Experience in the Application of Hydrocarbon Optical Studies in Oil Field Development // Energies. 2022. Vol. 15. Iss. 10. № 3626. DOI: 10.3390/en15103626
- Asemani M., Rabbani A.R., Sarafdokht H. Implementation of an Integrated Geochemical Approach Using Polar and Nonpolar Components of Crude Oil for Reservoir-Continuity Assessment: Verification with Reservoir-Engineering Evidences // SPE Journal. 2021. Vol. 26. Iss. 5. P. 3237-3254. № SPE-205388-PA. DOI: 10.2118/205388-PA
- Куклинский А.Я., Штунь С.Ю., Морошкин А.Н. и др. Применение методов резервуарной геохимии при оценке вклада в добываемую продукцию каждого из двух совместно эксплуатирующихся пластов, содержащих разные по молекулярному составу нефти // Геология, геофизика и разработка нефтяных и газовых месторождений. 2021. № 1 (349). С. 39-43. DOI: 10.33285/2413-5011-2021-1(349)-39-43
- Данцова К.И., Исказиев К.О., Хафизов С.Ф. Геохимическая характеристика органического вещества юрских отложений южных районов Западной Сибири // Нефтяное хозяйство. 2021. № 5. С. 50-53. DOI: 10.24887/0028-2448-2021-5-50-53
- Chen Q., Kristensen M., Johansen Y.B. et al. Analysis of Lateral Fluid Gradients From DFA Measurements and Simulation of Reservoir Fluid Mixing Processes Over Geologic Time // Petrophysics. 2021. Vol. 62. Iss. 1. P. 16-30. № SPWLA-2021-v62n1a1. DOI: 10.30632/PJV62N1-2021a1
- Рейтблат Е.А., Заночуев С.А., Гончаров И.В. и др. Изучение дифференциации состава и свойств газа пласта Ач3-4 на Ново-Уренгойском лицензионном участке // Газовая промышленность. 2021. № 12 (826). С. 46-52.
- Гончаров И.В., Веклич М.А., Обласов Н.В. и др. Природа углеводородных флюидов месторождений севера Западной Сибири (геохимический аспект) // Геохимия. 2023. T. 68. № 2. С. 115-138. DOI: 10.31857/S0016752523020048
- Мухаметшин В.Ш., Хакимзянов И.Н. Особенности группирования низкопродуктивных залежей нефти в карбонатных коллекторах для рационального использования ресурсов в пределах Урало-Поволжья // Записки Горного института. 2021. Т. 252. С. 896-907. DOI:10.31897/PMI.2021.6.11
- Галкин С.В., Кривощеков С.Н., Козырев Н.Д. и др. Учет геомеханических свойств пласта при разработке многопластовых нефтяных месторождений // Записки Горного института. 2020. Т. 244. С. 408-417. DOI: 10.31897/PMI.2020.4.3
- Ali Al-Amani Hj Azlan, Muda W.M.W., Mubaraki A.H. et al. New Approach of Synergizing Advanced Well Test Deconvolution, Rate Transient Analysis and Dynamic Modeling in Evaluating Reservoir Compartmentalization Uncertainty at K Field in Sarawak Basin; A Case Study // SPE Middle East Oil and Gas Show and Conference, 18-21 March 2019, Manama, Bahrain. OnePetro, 2019. № SPE-195038-MS. DOI: 10.2118/195038-MS
- Пылев Е.А., Чуриков Ю.М., Поляков Е.Е. и др. Оценка проводимости разломов по данным межскважинного гидро-прослушивания на Чаяндинском нефтегазоконденсатном месторождении // Вести газовой науки. 2021. № 3 (48). С. 192-202.
- Плюснин А.В., Гёкче М.И., Шаваров Р.Д., Никулин Е.В. Геодинамические и тектонические факторы формирования и разрушения карбонатных венд-кембрийских залежей углеводородов на юге Непско-Ботуобинской антеклизы // Геосферные исследования. 2023. № 1. С. 20-35.
- Pedersen K.S., Christensen P.L., Skaikh J.A. Phase behavior of petroleum reservoir fluids. Boca Raton: CRC Press, 2014. 465 p. DOI: 10.1201/b17887
- Høier L., Whitson C.H. Compositional Grading—Theory and Practice // SPE Reservoir Evaluation & Engineering. 2001. Vol. 4. Iss. 6. P. 525-535. № SPE-74714-PA. DOI: 10.2118/74714-PA
- Pedersen K.S., Hjermstad H.P. Modeling of Compositional Variation with Depth for Five North Sea Reservoirs // SPE Annual Technical Conference and Exhibition, 28-30 September 2015, Houston, TX, USA. OnePetro, 2015. № SPE-175085-MS. DOI: 10.2118/175085-MS
- Yazkov A.V., Gorobets V.E., Surkov E.V. et al. Complex Phase Behavior Study of a Near-Critical Gas Condensate Fluid in a Tight HPHT Reservoir // SPE Russian Petroleum Technology Conference, 26-29 October, 2020. OnePetro, 2020. № SPE-201997-MS. DOI: 10.2118/201997-MS
- Sajjad F.M., Chandra S., Ivan P. et al. The Effect of Compositional Gradient in Field Development // SPE/IATMI Asia Pacific Oil & Gas Conference and Exhibition, 12-14 October 2021. OnePetro, 2021. № SPE-205801-MS. DOI: 10.2118/205801-MS
- Gibbs J.W. The Collected Works of J. Willard Gibbs. Yale University Press, 1948. In 2 vol.
- Montel F., Gouel P.L. Prediction of Compositional Grading in a Reservoir Fluid Column // SPE Annual Technical Confe-rence and Exhibition, 22-26 September 1985, Las Vegas, NV, USA. OnePetro, 1985. № SPE-14410-MS. DOI: 10.2118/14410-MS
- Haase R., Borgmann H.-W., Dücker K.-H., Lee W.-P. Thermodiffusion im kritischen Verdampfungsgebiet binärer Systeme // Zeitschrift für Naturforschung A. 1971. Vol. 26. Iss. 7. P. 1224-1227. DOI: 10.1515/zna-1971-0722
- Хаазе Р. Термодинамика необратимых процессов. М.: Мир, 1967. 544 с.
- Pedersen K.S., Lindeloff N. Simulations of Compositional Gradients in Hydrocarbon Reservoirs under the Influence of a Temperature Gradient // SPE Annual Technical Conference and Exhibition, 5-8 October 2003, Denver, Colorado. OnePetro, 2003. № SPE-84364-MS. DOI: 10.2118/84364-MS
- Pedersen K.S., Fredenslund A., Thomassen P. Properties of oils and natural gases. Houston: Gulf Publishing Company, 1989. 252 p.
- Попов С.Б. Композиционное профилирование по глубине в газо-нефтяных месторождениях с температурным градиентом // Препринты Института прикладной математики им. М.В. Келдыша РАН. 2018. № 38. 32 с. DOI: 10.20948/prepr-2018-38
- Michelsen M.L. The isothermal flash problem. Part I. Stability // Fluid Phase Equilibria. 1982. Vol. 9. Iss. 1. P. 1-19. DOI: 10.1016/0378-3812(82)85001-2
- Попов С.Б. Композиционное профилирование по глубине в газо-нефтяных месторождениях // Препринты Института прикладной математики им. М.В.Келдыша РАН. 2017. № 61. 30 с. DOI: 10.20948/prepr-2017-61
- Whitson C.H., Belery P. Compositional Gradients in Petroleum Reservoirs // University of Tulsa Centennial Petroleum Engineering Symposium, 29-31 August 1994, Tulsa, OK, USA. OnePetro, 1994. № SPE-28000-MS. DOI: 10.2118/28000-MS
- Сурначев Д.В., Скибицкая Н.А., Индрупский И.М., Большаков М.Н. Оценка содержания и состава жидких углеводородов матричной нефти в газовой части продуктивных отложений нефтегазоконденсатных месторождений на примере Вуктыльского нефтегазоконденсатного месторождения // Актуальные проблемы нефти и газа. 2022. Вып. 1 (36). С. 42-65. DOI: 10.29222/ipng.2078-5712.2022-36.art3
- Skibitskaya N., Bolshakov M., Burkhanova I. et al. Tight Oil in Oil-And-Gas Source Carbonate Deposits’ Gas Saturation Zones of Gas-Condensate and Oil-Gas Condensate Fields // SPE Russian Petroleum Technology Conference and Exhibition, 24-26 October 2016, Moscow, Russia. OnePetro, 2016. № SPE-182076-MS. DOI: 10.2118/182076-MS
- Kusochkova E.V., Indrupskiy I.M., Kuryakov V.N. Distribution of the Initial Fluid Composition in an Oil-Gas-Condensate Reservoir with Incomplete Gravity Segregation // IOP Conference Series: Earth and Environmental Science. 2021. Vol. 931. № 012012. DOI: 10.1088/1755-1315/931/1/012012
- Whitson C.H., Michelsen M.L. The negative flash // Fluid Phase Equilibria. 1989. Vol. 53. P. 51-71. DOI: 10.1016/0378-3812(89)80072-X
- Reid R.C., Prausnitz J.M., Poling B.E. The Properties of Gases and Liquids. McGraw-Hill, 1987. 741 p.
- Wheaton R.J. Treatment of Variations of Composition With Depth in Gas-Condensate Reservoirs // SPE Reservoir Engineering. 1991. Vol. 6. Iss. 2. P. 239-244. № SPE-18267-PA. DOI: 10.2118/18267-PA
