Оценка влияния температуры рабочей жидкости на потери мощности карьерного гидравлического экскаватора

М. Г. Рахутин; Кхань Куок Занг; А. Е. Кривенко; Ван Хиеп Чан

Том 261

Страницы:

374-383

Скачать том:

RUS ENG

Научная статья

Энергетика

Оценка влияния температуры рабочей жидкости на потери мощности карьерного гидравлического экскаватора

Авторы:

М. Г. Рахутин¹

Кхань Куок Занг²

А. Е. Кривенко³

Ван Хиеп Чан⁴

Об авторах

1 — д-р техн. наук Национальный исследовательский технологический университет «МИСиС» ▪ Orcid
2 — канд. техн. наук преподаватель Куангниньский Индустриальный Университет ▪ Orcid
3 — канд. техн. наук Национальный исследовательский технологический университет «МИСиС» ▪ Orcid
4 — аспирант Национальный исследовательский технологический университет «МИСиС» ▪ Orcid

Дата отправки:

2023-03-16

Дата принятия:

2023-06-20

Дата публикации:

2023-07-19

Аннотация

В установившемся режиме работы температура рабочей жидкости гидравлической системы карьерного экскаватора определяется температурой окружающей среды, конструкцией гидравлической системы и потерями мощности. Величина потерь мощности зависит от физических и термодинамических свойств рабочей жидкости и степени износа рабочих элементов гидравлической системы карьерного экскаватора. Основными причинами потерь мощности являются гидравлические потери в местных сопротивлениях, трубопроводах и утечки в насосах и гидромоторах. При увеличении температуры рабочей жидкости ее вязкость уменьшается, что приводит к снижению потерь мощности за счет гидравлических потерь в трубопроводах и местных сопротивлениях и к увеличению объемных утечек и связанных с ними потерь мощности. Для численного определения уровня потерь мощности на примере экскаватора Komatsu PC750-7 при применении гидравлических масел Shell Tellus S2 V 22, 32, 46, 68 с соответствующей кинематической вязкостью 22, 32, 46, 68 сСт при 40 °C использовалась разработанная методика расчета и программный алгоритм в среде MatLab Simulink. Предложен коэффициент потери мощности, получаемый сравнением потерь мощности при оптимальной величине температуры для гидросистемы в рассматриваемых условиях с фактическими. Использование коэффициента позволит выбирать рабочие жидкости и устанавливать величины предельного состояния основных насосов и других элементов гидросистемы, оценивать фактическую энергоэффективность работы экскаватора. Расчеты показали, что проведение мероприятий, обеспечивающих работу в интервале с отклонением 10 % от оптимального значения температуры для данных условий, позволяет сократить потери энергии от 3 до 12 %.

Ключевые слова:

карьерный гидравлический экскаватор гидравлическая система потеря мощности вязкость температура утечки рабочей жидкости гидравлические потери

Введение

Общеизвестно, что в большинстве гидравлических систем КПД не превышает 75 %. Подведенная мощность при этом расходуется на преодоление механического трения, гидравлические потери в трубопроводах и местных сопротивлениях, внутренние утечки рабочей жидкости. Все потери мощности превращаются в тепло, поглощаемое рабочей жидкостью [1-3]. Рост температуры рабочей жидкости выше определенного предела приводит к возрастанию скорости старения, ухудшению рабочих свойств и существенно влияет на производительность экскаватора и долговечность гидравлической системы. Особое значение потери мощности имеют при эксплуатации карьерных гидравлических экскаваторов, поскольку они работают в режиме изменяющихся внешних условий, в первую очередь температуры окружающей среды, и имеют мощный привод, что дает большие абсолютные значения потерь электрической энергии или дизельного топлива [4-6].

Расчет потерь мощности позволит выбрать соответствующую мощность привода при проектировании новой техники, найти условия теплового равновесия, определить максимально возможную температуру масла в гидравлической системе экскаватора, правильно выбрать параметры маслоохладителя с учетом мощности, режима и условий эксплуатации оборудования. Точный расчет суммарных потерь мощности гидравлической системы карьерного экскаватора сложен из-за большого объема вычислений и необходимости учета изменчивости физических параметров сред, участвующих в процессе.

Методы

В качестве объекта изучения выбрана гидравлическая система экскаватора Komatsu PC750-7. Рабочие жидкости Shell Tellus S2 V 22, 32, 46, 68 с соответствующей кинематической вязкостью 22, 32, 46, 68 сСт при 40 °C. Механические потери в узлах трения приняты постоянной величиной и при расчетах не учитывались [7, 8].

В гидравлической системе карьерного экскаватора потери энергии зависят от выполняемых операций и температуры рабочей жидкости. Это мощность, расходуемая на преодоление сопротивления в гидравлических магистралях, местных сопротивлениях и утечки рабочей жидкости в элементах гидравлической системы. Для точной оценки потерь энергии в гидросистеме экскаватора необходимо учитывать зависимость плотности и вязкости рабочей жидкости от температуры. В расчетах, выполняемых вручную, принято усреднять физические параметры рабочей жидкости, поскольку учет изменения плотности и вязкости от температуры значительно усложняет вычисления.

Изменение плотности и вязкости рабочей жидкости в широком диапазоне температур влияет на энергоемкость процессов передачи и преобразования энергии, протекающих в гидравлической системе карьерного экскаватора, и для получения точных результатов необходим учет этих изменений. С изменением температуры изменяется величина каждого типа потерь мощности. С ростом температуры рабочей жидкости уменьшается ее вязкость, что влечет за собой уменьшение потерь мощности из-за гидравлических потерь в трубопроводах и местных сопротивлениях и одновременно увеличение потерь мощности из-за возрастания объема утечек в элементах гидравлической системы.

Изменение плотности рабочей жидкости в рабочем диапазоне температур влияет на величину потерь мощности, носит линейный характер и может быть определено по формуле [9-11]

ρ_{t} = \frac{ρ_{0}}{1 + α_{t} Δ t},

где ρ₀, ρ_t – плотность рабочей жидкости при температуре t₀ и t, кг/м³; Δt – изменение температуры, °С; α_t – коэффициент температурного расширения, °C^–1.

Изменение вязкости рабочей жидкости при изменении температуры в диапазоне 40-110 °С определяется из выражения

ν_{t} = ν_{0}^{{(\frac{t_{0}}{t})}^{n}},

где ν₀, ν_t – кинематический коэффициент вязкости при температуре t₀ и t, м²/с; n – коэффициент, зависящий от типа и марки рабочей жидкости, температуры t₀ и вязкости ν₀ [9, 10, 12].

В диапазоне температур от 0 до 40 °С выражение для расчета кинематической вязкости принимает следующий вид:

ν_{t} = a t^{2} + b t + c,

где a, b, c – коэффициенты, зависящие от температуры и характеристик рабочей жидкости, определяются по справочной литературе или экспериментально. Их значения для рабочей жидкости Shell Tellus S2 V 46 в интервалах температуры до 40 °C представлены в табл.1.

Таблица 1

Значения коэффициентов для рабочей жидкости Shell Tellus S2 V 46

Интервал температуры t	Коэффициенты
Интервал температуры t	а	b	c
0-10	0,9	–30,5	430
10-20	0,6	–28	435
20-30	0,14	–11,3	285
30-40	0,04	–5,4	198

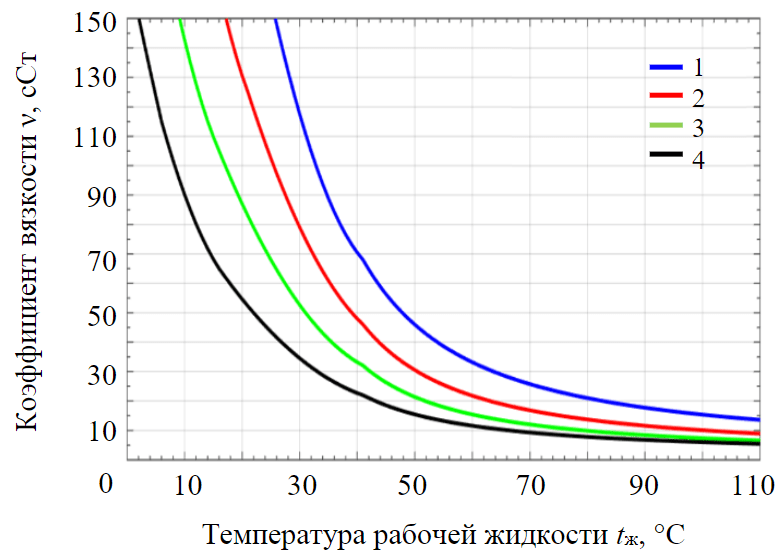
Рис.1. Зависимость вязкости рабочих жидкостей от температуры 1 – Shell Tellus S2 V 68; 2 – S2 V 46; 3 – S2 V 32; 4 – S2 V 22

Зависимость вязкости применяемых в карьерных гидравлических экскаваторах рабочих жидкостей Shell Tellus от температуры показана на рис.1.

Расчет потерь мощности при работекарьерногогидравлического экскаватора предполагает расчет гидравлических потерь по длине трубопроводов и местных сопротивлений, потерь мощности из-за утечек, в первую очередь основных насосов и гидромоторов. Суммарные гидравлические потери по длине трубопроводной системы определяются по формуле Дарси – Вейсбаха для потока вязкой жидкости

\sum Δ p_{l} = ρ g \sum_{i = 1}^{n} (λ_{i} \frac{L_{i}}{d_{i}} \frac{v_{i}^{2}}{2 g}) = \frac{ρ}{2} \sum_{i = 1}^{n} (λ_{i} \frac{L_{i}}{d_{i}} v_{i}^{2}),

где i – количество прямых участков гидравлической трубы; λ_i– коэффициент гидравлического трения для соответствующей гидролинии; L_i, d_i – длина и внутренний диаметр i-го трубопровода; v_i – средняя скорость потока рабочей жидкости i-го трубопровода [10, 13, 14].

Величина коэффициента гидравлического трения зависит от характера течения жидкости. После длительного простоя, сразу после запуска гидросистемы, когда жидкость еще не прогрелась, в каналах может наблюдаться ламинарное течение и коэффициент гидравлического трения принято подсчитывать по формуле Пуазейля [10, 14, 15]

λ = \frac{64}{Re} .

Далее при турбулентном режиме по формуле Блазиуса [14-16] определяется

λ = 0,3164 {Rе}^{- 0,25},

где Re – число Рейнольдса потока рабочей жидкости в трубопроводе.

Также потери возникают, когда жидкость проходит через местные сопротивления: фитинги, клапаны, управляющие устройства гидросистемы. Величину потерь давления рассчитывают по формуле [14, 17]

\sum Δ p_{ф} = \sum_{j = 1}^{J} ρ g K_{j} (\frac{ν_{j}^{2}}{2 g}) = \frac{ρ}{2} \sum_{j = 1}^{J} K_{j} ν_{j}^{2},

где K – коэффициент местных потерь давления, значения определяются по справочной литературе или экспериментально.

Рабочий цикл рабочей камеры аксиально-поршневого насоса состоит из процессов всасывания и нагнетания рабочей жидкости. Причиной утечек рабочей жидкости в насосе служит большая разница давлений между рабочей камерой и корпусом. Объемные потери возникают, когда происходит вытеснение жидкости в напорную магистраль. Утечки рабочей жидкости из рабочей камеры складываются из четырех компонентов: утечки через зазор между плунжером и стенкой цилиндра Q_рс; через зазор между плунжером и башмаком Q_р_s; через зазор между башмаком и упорным диском Q_ss; через зазор между блоком цилиндров и pacпpeдeлитeльным диском Q_cv (рис.2, а).

Утечки рабочей жидкости через кольцевой зазор между плунжером и стенкой цилиндра определяются по выражению [10, 17, 18]

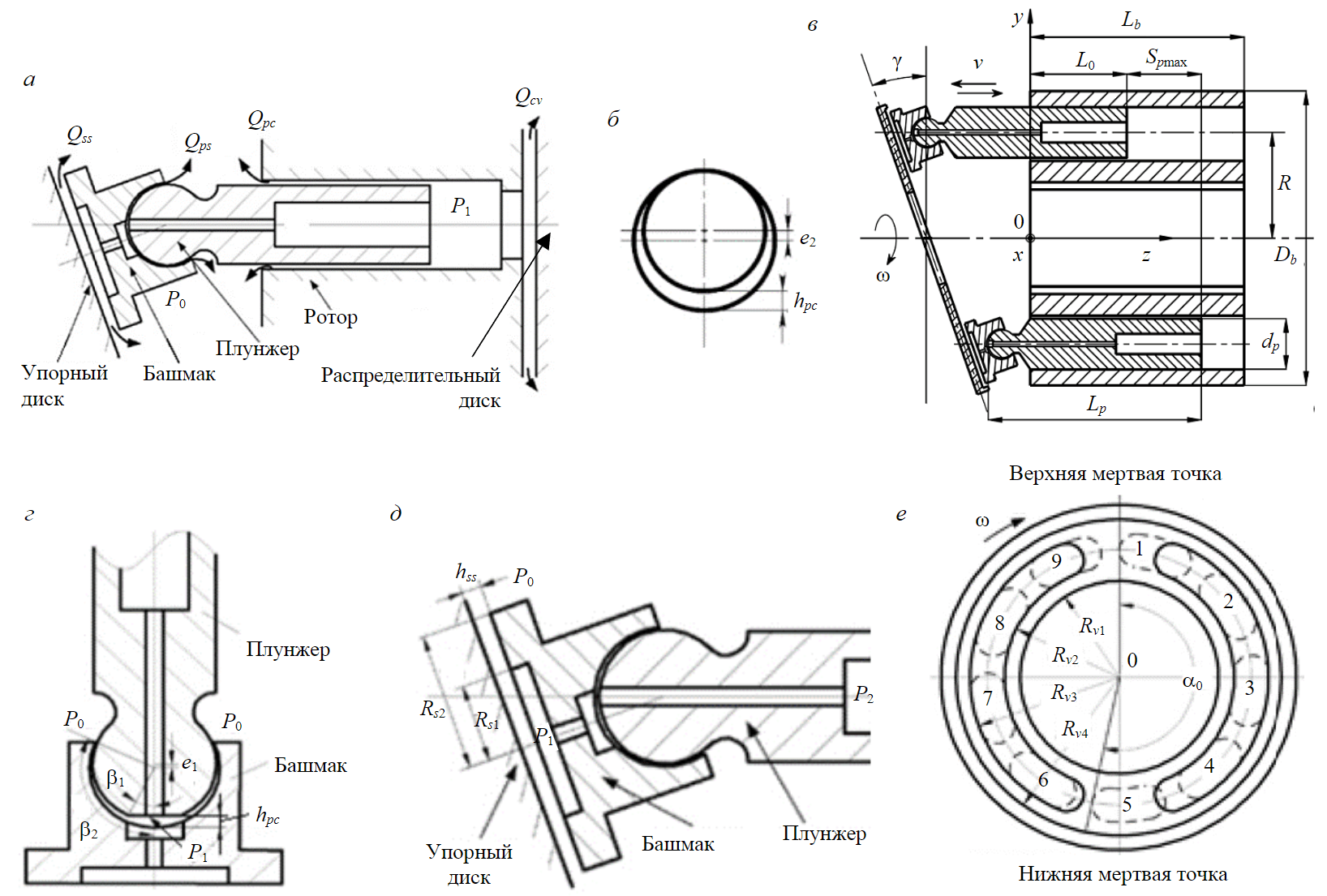
Q_{р c} = \frac{π d_{р} h_{р c}^{3} (P_{1} - P_{0})}{12 μ l} (1 + 1,5 η^{2}) - \frac{π d_{р} h_{р c} v}{2}, (1)

Рис.2. Утечки рабочей жидкости в аксиально-плунжерных насосе и гидромоторе

где d_p – диаметр плунжера, м; h_pc – ширина зазора между плунжером и цилиндром, м; P₁, P₀ – давление в рабочей камере насоса и в корпусе, Па; μ динамический коэффициент вязкости рабочей жидкости, Па·с; l – длина плунжера в цилиндре, м; η = e/h_pc – относительный эксцентриситет; e – эксцентриситет плунжера относительно цилиндра, м; v – скорость движения плунжера в рабочей камере, м/с (рис.2, б, в) [10].

Утечки рабочей жидкости в сферическом шарнире между плунжером и башмаком определяются по выражению [10, 17, 18]

Q_{р s} = \frac{π h_{р s}^{3} (P_{1} - P_{0})}{3 μ ({tg}^{2} β_{2} - {tg}^{2} β_{1} + 2 ln |\frac{{tgβ}_{2}}{{tgβ}_{1}}|)}, (2)

где h_ps– ширина зазора сферического шарнира, м; P₁, P₀ – давление в камере башмака и в корпусе насоса, Па; β₁, β₂ – конструктивные углы сферического сочленения плунжера и башмака, рад (рис.2, г).

Утечки рабочей жидкости через зазор между башмаком и упорным диском определяются по формуле [10, 18, 19]

Q_{s s} = \frac{π h_{s s}^{3} (P_{1} - P_{0})}{6 μln (R_{s 2} / R_{s 1})}, (3)

где h_ss– ширина зазора между башмаком и упорным диском, м; R_s₁ – радиус проточки, м; R_s₂ – наружный радиус башмака плунжера, м (рис.2, д).

Утечки рабочей жидкости через зазор между блоком цилиндров и распределительным диском определяются по выражению [10, 18, 20]

Q_{c v} = \frac{α_{0} h_{c v}^{3} (P_{s} - P_{0})}{12 μ} [\frac{1}{ln (R_{v 2} / R_{v 1})} + \frac{1}{ln (R_{v 4} / R_{v 3})}], (4)

где h_cv – ширина зазора между блоком цилиндров и распределительным диском, м; R_v₁, R_v₂, R_v₃, R_v₄ – размеры распределительного диска, м (рис.2, е).

Суммируя результаты формул (1)-(4), с учетом рабочего цикла камер и конструкции насоса получим

Q_{п 1} = \frac{z}{2} (Q_{р c} + Q_{р s} + Q_{s s} + Q_{c v}),

где z – число рабочих камер в насосе.

Принимая во внимание допущения, общие потери мощности в гидравлической системе карьерного экскаватора можно записать в виде [21-23]

Δ N = \frac{Q_{э} Δ p + Q_{п 1} p}{1000},

где Q_э –объемный расход рабочей жидкости, м³/с; Δp – потери давления в гидравлической системе, Па; Q_п1 – суммарные утечки рабочей жидкости в насосах и гидромоторах, м³/с; р – рабочее давление в гидросистеме, Па.

Математическая модель, используемая для программирования вычислений с использованием программного обеспечения MatLab Simulink, построена на основе рассмотренных уравнений и выражений. Основными параметрами, использованными в расчетах и моделировании, являются фактические параметры гидравлической системы карьерного экскаватора Komatsu PC750-7 по данным каталога производителя (табл.2).

Таблица 2

Исходные параметры для моделирования

Элемент системы	Параметры
Рабочая жидкость Shell Tellus S2 V 440 л	Плотность при t_ж= 15 °C: ρ = 872 кг/м³
Главный гидронасос HPV160+160 2 шт.	Диаметр рабочей камеры d_p = 22,5 мм
	Длина плунжера L_p = 100 мм
	Радиус окружности осей рабочих камер R_p = 49,5 мм
	Угол наклона упорного диска γ = 19,5°
	Минимальная длина плунжера в рабочей камере l₀ = 45 мм
	Количество рабочих камер z = 9
	Частота вращения n = 2400 об/мин
	Давление в рабочей камере P_s = 31 МПa
	Давление в корпусе P₀ = 1,5 МПa
	Конструктивные размеры упорного башмака плунжера R_s₁ = 8 мм; R_s₂ = 13°
	Конструктивные углы сферического сочленения плунжера и башмака b₁ = 14°; b₂ = 119°
	Конструктивные размеры распределительного узла R_v₁ = 29 мм; R_v₂ = 38 мм; R_v₃ = 50 мм; R_v₄ = 60 мм; a₀ = 193°
Гидромоторы поворота платформы(аксиально-плунжерные) 2 шт.	Рабочий объем q₁ = 255 см³/об
	Частота вращения 260 об/мин
	Рабочее давление 28,4 МПа
	Мощность 31,4 кВт
	Механический КПД η_мех = 0,98
	Объемный КПД η_о = 0,96
Гидроцилиндры подъема стрелы 2 шт.	Расходы в процессах:
	копания 0,0018 м³/с
	подъема и поворота 0,0013 м³/с
	разгрузки 0,0014 м³/с
	возврата и опускания 0,00144 м³/с
	Внутренний диаметр гидролиний d_тр_in = 19,05 мм
	Длина гидролиний L_тр = 13,4 м
Гидроцилиндры рукояти 2 шт.	Расходы в процессах:
	копания 0,002 м³/с
	подъема и поворота 0,00014 м³/с
	разгрузки 0,00105 м³/с
	возврата и опускания 0,001903 м³/с
	Внутренний диаметр гидролиний d_тр_in = 19,05 мм
	Длина гидролиний L_тр = 23 м
Гидроцилиндры ковша 1 шт.	Расходы в процессах:
	копания 0,00191 м³/с
	подъема и поворота 0,001804 м³/с
	разгрузки 0,0021 м³/с
	возврата и опускания 0,00115 м³/с
	Внутренний диаметр гидролиний d_тр_in = 19,05 мм
	Длина гидролиний L_тр = 23 м
Маслоохладитель 1 шт.	Размеры овальных труб в маслоохладителе: a = 22,1 мм; b = 6 мм; δ_тр = 0,75 мм
	Число рядов труб z_ряд = 3
	Число труб в ряду m_{колонки} = 51
	Длина труб L_тр = 1290 мм
Фильтры 5 шт.	Коэффициенты местных сопротивлений 5-12
Распределитель 3 шт.	Коэффициенты местных сопротивлений 3-5
Дpocсeль 3 шт.	Коэффициенты местных сопротивлений 0-100
Стандартный угольник 90° 34 шт.	Коэффициенты местных сопротивлений 1
Обратный клапан 5 шт.	Коэффициенты местных сопротивлений 1-5
Всасывающая линия насоса	Диаметр 35 мм
Всасывающая линия насоса	Длина 2,5 м

Численное моделирование физических процессов нашло широкое применение в области исследования процессов карьерных гидравлических экскаваторов, поскольку позволяет учитывать величины, изменяющиеся по нелинейным зависимостям, и решить ранее рассматривавшиеся задачи с существенно большей точностью [24-26]. Для компьютерного моделирования потерь мощности в гидравлической системе использовалась разработанная методика расчета и программный алгоритм, реализованный в среде MatLab Simulink.

Обсуждение результатов

Подготовка численного эксперимента потребовала проведения анализа рабочего цикла карьерного гидравлического экскаватора Komatsu PC750-7 [27-29]. Были установлены точные значения скоростей потоков на различных участках гидравлических линий, а также в отдельных устройствах гидравлической системы экскаватора, что важно для точного определения потерь энергии [30-32]. В результате моделирования получены значения потерь мощности в процессе выполнения рабочих операций при различных значениях температур (табл.3).

Таблица 3

Потери мощности в процессе выполнения рабочих операций, кВт

Температура рабочей жидкости t_ж, °С	Копание	Подъем и поворот	Разгрузка	Возврат и опускание	Объемные утечки
0	390,2	110,3	269,3	222,5	1,6
20	126,3	41,73	90,08	76,23	5,99
30	90,78	32,44	65,92	56,42	9,64
40	71,43	27,51	52,34	45,74	15,2
50	58,41	24,34	43,69	38,73	24
55	54,66	23,39	41,16	36,68	28,71
60	51,87	22,69	39,28	35,15	33,56
70	48,04	21,71	36,69	33,04	43,51
80	45,54	21,07	35,02	31,67	53,62
90	43,8	20,61	33,85	30,71	63,76
110	41,52	20,02	32,33	29,45	83,78

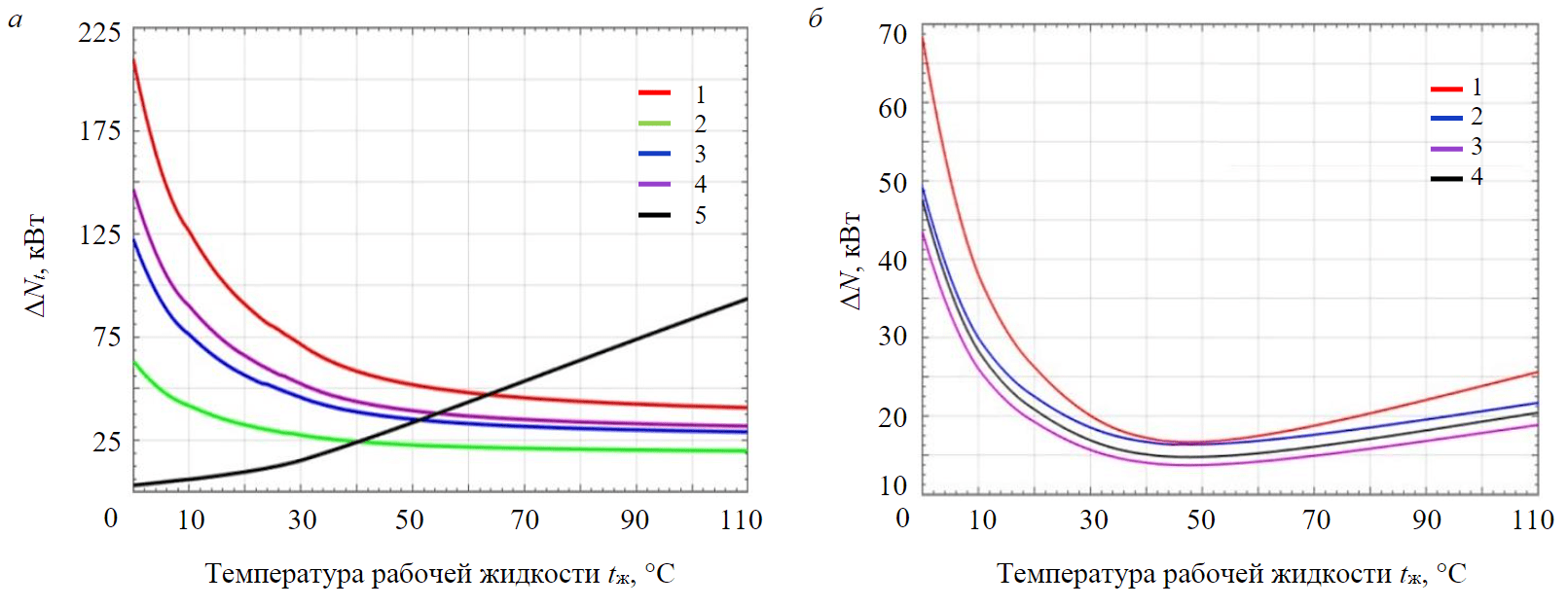
Рис.3. Потери мощности в зависимости от температуры рабочей жидкости: а – из-за объемных утечек, гидравлических потерь по длине трубопроводов, местных сопротивлений (1 – в процессе копания; 2 – подъема и поворота; 3 – возврата и опускания; 4 – разгрузки; 5 – в основных гидронасосах) б – суммарные потери мощности при осуществлении рабочих процессов (1 – копания; 2 – подъема и поворота; 3 – разгрузки; 4 – возврата и опускания)

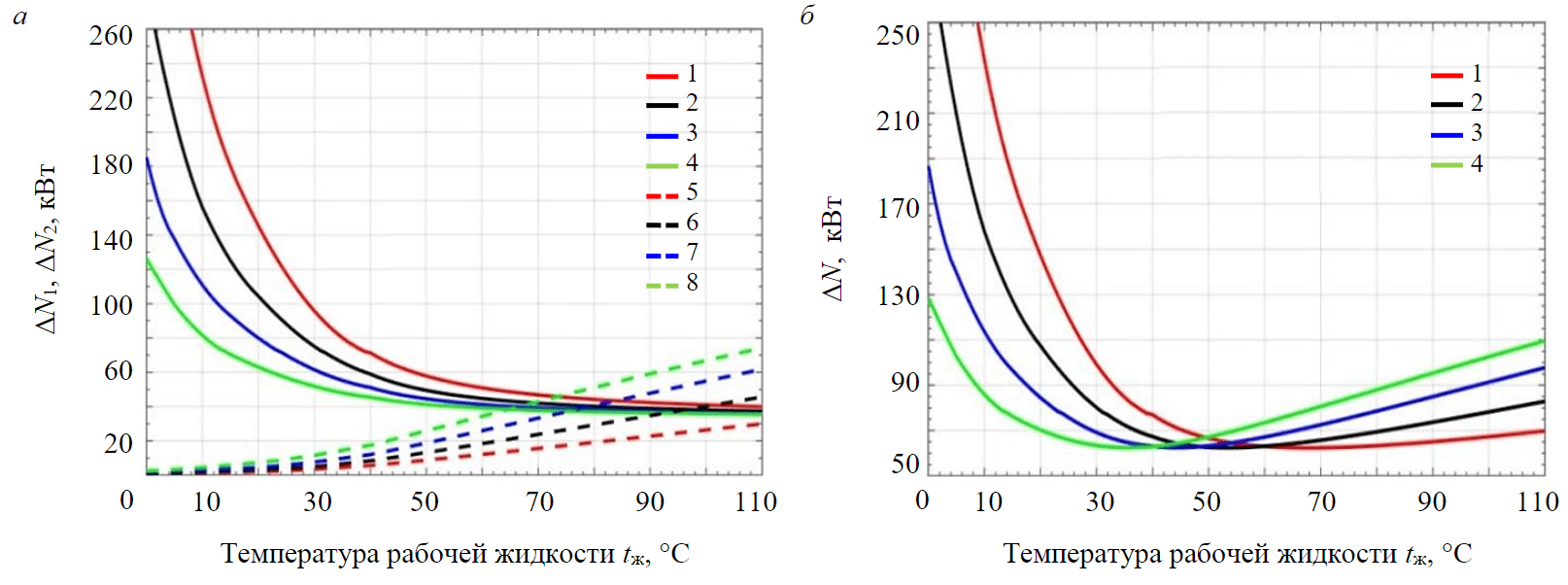
Рис.5. Изменение значений коэффициента потери мощности в зависимости от температуры 1 – ΔN_min/Δ*N_t* при использовании Shell Tellus S2 V 68; 2 – при Shell Tellus S2 V 46; 3 – при Shell Tellus S2 V 32; 4 – при Shell Tellus S2 V 22

На рис.3 представлены потери мощности из-за объемных утечек, гидравлических потерь по длине трубопроводов и местных сопротивлений в зависимости от температуры рабочей жидкости для операций копания горной массы, подъема и поворота, разгрузки, возврата и опускания рабочего оборудования.

Из представленных графических зависимостей наглядно видно, что потери энергии при различных рабочих операциях существенно отличаются друг от друга, что не противоречит ранее публиковавшимся результатам [33-35]. По мере увеличения температуры жидкости потери мощности из-за гидравлических потерь по длине трубопроводов и местных сопротивлений будут уменьшаться, тогда как потери мощности из-за объемных утечек увеличиваются.

Значения суммарных потерь мощности ∆N при различных операциях рабочего цикла экскаватора отличаются по величине, но все они имеют общую особенность: суммарные потери мощности уменьшаются с увеличением температуры рабочей жидкости от 0 до 30-35 °С, достигая самого низкого значения в диапазоне температур от 35 до 55 °С. После 55 °С потери мощности быстро повышаются с ростом температуры. Поскольку утечки в управляющих устройствах гидравлической системы на этом этапе исследований не учитывались, потери мощности с повышением температуры в рассматриваемом примере будут являться нижней границей значений.

Общие потери мощности в зависимости от температуры для различных рабочих жидкостей представлены на рис.4. Графические зависимости наглядно показывают существенный перерасход энергии при работе на непрогретом гидравлическом масле и необходимость его прогрева перед началом работы до 30-40 °С.

Из данных зависимостей следует, что при работе экскаватора в зимних условиях целесообразно использовать рабочие жидкости с меньшей вязкостью, а при работе в жарком климате, например в условиях Вьетнама, применять рабочие жидкости с повышенной вязкостью. Оптимальное значение температуры зависит от вязкости и других характеристик жидкости, от технического состояния элементов гидросистемы и горно-технических факторов эксплуатации, влияющих на продолжительность рабочих циклов, поэтому абсолютные потери мощности в определенных условиях не являются информативным показателем.

Для оценки энергоэффективности гидравлической системы карьерного экскаватора предложен коэффициент потери мощности, определяемый как отношение минимально возможных потерь мощности в гидросистеме в рассматриваемых условиях эксплуатации к фактическим:

K_{пм} = \frac{Δ N_{min}}{Δ N_{ф}},

где ΔN_min – минимально возможные потери мощности в данных условиях; ΔN_ф – фактические потери мощности.

Значения коэффициентов потери мощности при использовании рабочих жидкостей представлены на рис.5. Предложено понятие «температурный интервал потери мощности Т_ипм» – интервал между минимальной и максимальной температурами, соответствующими значению коэффициента потери мощности.

Диапазон температур при значении коэффициента потерь мощности 0,8; 0,9; 0,95 для жидкостей с различной вязкостью в рассматриваемых условиях представлен в табл.4: ν – вязкость рабочей жидкости; t_opt– значение температуры для наименьших потерь энергии; t_–А, t_+А– наименьшее и наибольшее значения температуры в рассматриваемом интервале; t_–От, t_+От – величина интервала температуры от t_opt до t_–А, t_+А; t₊-t_– – величина интервала температуры от t_–А до t_+А.

Таблица 4

Значения диапазона температур при различной вязкости рабочих жидкостей

ν, сСт	t_opt	K_пм = 0,8					K_пм = 0,9					K_пм = 0,95
ν, сСт	t_opt	t_–_А	t_–От	t_+А	t_+От	t₊-t_–	t_–А	t_–От	t_+А	t_+От	t₊-t_–	t_–А	t_–От	t_+А	t_+От	t₊-t_–
22	35	12	23	68	33	56	20	15	52	17	32	25	10	45	10	15
32	44	24	20	79	35	55	30	14	62	18	32	32	12	53	9	21
46	55	30	25	100	45	70	38	17	80	35	42	42	13	70	15	28
68	68	40	28	> 110	> 45	80	48	20	108	50	60	52	16	95	27	43

Из графических зависимостей и данных, представленных в табл.4, следует, что с увеличением вязкости увеличивается разность значений высокой и оптимальной температуры, а также величина интервала потери мощности, соответствующие заданному значению К_пм.

Заключение. Предложена методика расчета потерь мощности в гидросистеме карьерного гидравлического экскаватора в зависимости от температуры, реализованная с использованием программы MatLab Simulink на примере рабочей жидкости Shell Tellus SV 2 46 и гидросистемы экскаватора Komatsu PC750-7.

В диапазоне от 0 до 30-50 °С 70-80 % потерь мощности составляют гидравлические потери в трубопроводах и местных сопротивлениях, которые уменьшаются по квадратической зависимости с уменьшением вязкости рабочей жидкости, вызванной увеличением температуры. После 30-50 °С при дальнейшем уменьшении вязкости рабочей жидкости из-за увеличения утечек в насосах и гидромоторах основные потери мощности возрастают по зависимости, близкой к прямой. Угол наклона зависимости определяется техническим состоянием гидромоторов и насосов, в первую очередь основных насосов, параметрами рабочей жидкости и горно-техническими факторами эксплуатации.
Предложен критерий оценки потерь энергии в гидросистеме карьерного гидравлического экскаватора в зависимости от температуры рабочей жидкости – коэффициент потерь мощности K_пм, получаемый сравнением минимально возможных потерь при оптимальной температуре в данных условиях с потерями энергии при фактической температуре. Использование коэффициента позволит оценивать «излишние» потери энергии при отклонении от диапазона, близкого к оптимальной температуре рабочей жидкости в рассматриваемых условиях и гидравлических системах других машин.
Предложено понятие «температурный интервал потери мощности Т_ипм» – интервал между минимальной и максимальной температурами, соответствующими значению коэффициента потери мощности.
Расчеты показали, что проведение мероприятий, обеспечивающих работу в интервале с отклонением 10 % от оптимального значения температуры (K_пэ ≥ 0,9) для данных условий, позволяет сократить потери энергии от 3 до 12 %.

Литература

Пудов Е.Ю., Занг К.К., Кузин Е.Г., Кривенко А.Е. Оценка влияния условий эксплуатации на производительность работы системы охлаждения рабочей жидкости гидравлического карьерного экскаватора // Горное оборудование и электромеханика. 2021. № 1. С. 51-58. DOI: 10.26730/1816-4528-2021-1-51-58
Özmen Ö., Sınanoğlu C., Batbat T., Güven A. Prediction of Slipper Pressure Distribution and Leakage Behaviour in Axial Piston Pumps Using ANN and MGGP // Mathematical Problems in Engineering. Vol. № 7317520. P. 1-13. DOI: 10.1155/2019/7317520
Bergada J.M., Kumar S., Davies D.L., Watton J. A complete analysis of axial piston pump leakage and output ﬂow ripples // Applied Mathematical Modelling. Vol.36. Iss. 4. P. 1731-1751. DOI: 10.1016/j.apm.2011.09.016
Комиссаров А.П., Лагунова Ю.А., Шестаков В.С., Иванов И.Ю. Энергопотребление одноковшовых экскаваторов // Горный журнал. 2018. № 1. С. 73-77. DOI: 17580/gzh.2018.01.13
Juza M., Hermanek P. Study of the energy efficiency of the UDS 214 excavator hydraulic system // MM Science Journal. 2022. Iss. 3. P. 5768-5774. DOI: 10.17973/MMSJ.2022_10_2022077
Casoli, Scolari F., Vescovini C.M. et al. Excavator hydraulic circuit solution to reduce dissipations and fuel consumption // E3S Web of Conferences. 2021. Vol. 312. № 05004. DOI: 10.1051/e3sconf/202131205004
Balakhnina E., Vykhodtseva G., Sizova E. et al. Theoretical interpretation of the function of changing the tractive effort of a quarry locomotive in the starting mode // AIP Conference Proceedings. International Conference on Modern Trends in Manufacturing Technologies and Equipment 2021, 6-10 September 2021, Sevastopol, Russia. AIP Publishing, Vol. 2503. Iss.1. № 050049. DOI: 10.1063/5.0100861
Balakhnina, SizovaE., VykhodtsevaG., MishedchenkoO. Investigation of the Dependence of the Friction Coefficient Change on the Speed under Rational Starting Modes of a Quarry Locomotive // AIP Conference Proceedings, International Conference on Modern Trends in Manufacturing Technologies and Equipment 2021, 6-10 September 2021, Sevastopol, Russia. AIP Publishing, 2022. Vol. 2503. Iss. 1. № 050048. DOI: 10.1063/5.0100597
Пудов Е.Ю., Занг К.К., Кузин Е.Г. и др. Влияние температуры окружающей среды и типа рабочей жидкости на термодинамическое равновесие гидравлической системы карьерных экскаваторов // Горное оборудование и электромеханика. 2021. № С. 45-50. DOI: 10.26730/1816-4528-2021-1-45-50
Занг К.К. Обоснование и выбор параметров охладителя гидросистемы карьерного гидравлического экскаватора при эксплуатации в условиях Республики Вьетнам: Автореф. дис. … канд. техн. наук. М.: МИСиС, 2021. 21 с.
AbduazizovN.A., MuzaffarovA., ToshovJ.B. etal. A complex of methods for analyzing the working fluid of a hydrostatic power plant for hydraulic mining machines // International Journal of Advanced Science and Tehnology. Vol. 29. SI5. P. 852-855.
Абдуазизов Н.А., Джураев Р.У., Жураев А.Ш. Исследование влияния температуры и вязкости рабочей жидкости гидравлических систем на надежность работы горного оборудования // Горный вестник Узбекистана. № 3 (74). С.58-60. DOI: 10.13140/RG.2.2.11942.96329
Xia Lianpeng, Quan Long, Cao Donghui et a Research on Energy Saving Characteristics of Large Hydraulic Excavator Boom Driven by Dual Hydraulic-gas Energy Storage Cylinder // Journal of Mechanical Engineering. 2019. Vol. 55. Iss. 20. P.240-248. DOI: 10.3901/JME.2019.20.240
Yusuf S.I., Ejeh S., Olayiwola R.O. Analytical Study of Leakage of Viscous Flow in a Cylindrical Pipe // International Journal of Scientific Engineering and Applied Science. 2022. Vol. 8. Iss. 3. P. 74-93.
SiddiqueA.A., Yong-Joo Kim, Wan-Soo Kim et al. Effects of Temperatures and Viscosity of the Hydraulic Oils on the Proportional Valve for a Rice Transplanter Based on PID Control Algorithm // Agriculture. 2020. Vol.10. Iss.3. № 73. DOI: 10.3390/agriculture10030073
Lukashuk O.A., Komissarov A.P., Letnev K.Y. Increasing power efficiency of open-pit excavators // IOP Conference Series: Materials Science and Engineering. 2020. 709. Iss. 2. № 022083. DOI: 10.1088/1757-899X/709/2/022083
Ruichuan Li, Jilu Liu, Xinkai Ding, Qi Liu. Study on the Influence of Flow Distribution Structure of Piston Pump on the Output of Pulsation Pump // Processes. 2022. Vol.10. Iss. № 1077. DOI: 10.3390/pr10061077
Haocen Hong, Chunxiao Zhao, Bin Zhang et al. Flow Ripple Reduction of Axial-Piston Pump by Structure Optimizing of Outlet Triangular Damping Groove // Processes. 2020. Vol. 8. Iss.12. № DOI: 10.3390/pr8121664
Shishlyannikov D., Zverev V., Ivanchenko A., Zvonarev I. Increasing the Time between Failures of Electric Submersible Pumps for Oil Production with High Content of Mechanical Impurities // Applied Sciences. 2022. Vol. Iss.1. № 64. DOI: 10.3390/app12010064
Xingjian Wang, Siru Lin, Shaoping Wang et al. Remaining useful life prediction based on the Wiener process for an aviation axial piston pump // Chinese Journal of Aeronautics. 2016. Vol. 29. Iss. 3. P. 779-7 DOI: 10.1016/j.cja.2015.12.020
Yingxiao Yu, Tri Cuong Do, Bifeng Yin, Kyoung Kwan Ahn. Improvement of Energy Saving for Hybrid Hydraulic Excavator with Novel Powertrain // International Journal of Precision Engineering and Manufacturing-Green Technology. 2023.10. Iss. 2. P. 521-534. DOI: 10.1007/s40684-022-00437-9
Hidayat H., Aviva, Muis A. et al. Failure analysis of excavator hydraulic pump // IOP Conference Series: Materials Science and Engineering. 2022. Vol. 1212. Iss. 1. № 012052. DOI: 10.1088/1757-899X/1212/1/012052
Макарова В.В., Лагунова Ю.А., Ковязин Р.А., Нестеров В.И. Новый подход к созданию гидравлических экскаваторов // Горное оборудование и электромеханика. 2021. №6. C.9-14. DOI: 10.26730/1816-4528-2021-6-9-14
Литвин О.И., Марков С.О., Хорешок А.А. и др. Определение области энергоэффективного положения рабочего оборудования и эффективного радиуса черпания гидравлических экскаваторов на открытых горных работах // Маркшейдерия и недропользование. 2022. № 4 (120). С. 38-44. DOI: 10.56195/20793332_2022_4_38
Kujundžić T., KlanfarM., KormanT., Briševac Z. Influence of Crushed Rock Properties on the Productivity of a Hydraulic Excavator // Applied Sciences. 2021. 11. Iss. 5. № 2345. DOI: 10.3390/app11052345
Holt G.D., Edwards D. Analysis of interrelationships among excavator productivity modifying factors // International Journal of Productivity and Performance Management. Vol. 64. № 6. P.853-869. DOI: 10.1108/IJPPM-02-2014-0026
Комиссаров А.П., Лагунова Ю.А., Лукашук О.А., Шестаков В.С. Программное управление процессом экскавации горных пород карьерным экскаватором // Горное оборудование и электромеханика. 2020. № 5. С. 28-33. DOI: 10.26730/1816-4528-2020-5-28-33
Литвин О.И., Хорешок А.А., Дубинкин Д.М. и др. Анализ методик расчета производительности карьерных гидравлических экскаваторов // Горная промышленность. 2022. № 5. С. 112-120. DOI: 30686/1609-9192-2022-5-112-120
Комиссаров А.П., Лагунова Ю.А., Набиуллин Р.Ш., Хорошавин С.А. Цифровая модель процесса экскавации горных пород рабочим оборудованием карьерного экскаватора // Горный информационно-аналитический бюллетень. 2022. № 4. С. 156-168. DOI: 10.25018/0236_1493_2022_4_0_156
Litvin O., Litvin Y. Evaluation of Effect of the Excavator Cycle Duration on its Productivity // E3S Web of Conferences. Vol. 1 № 01010. P. 1-5. DOI: 10.1051/e3sconf/202017401010
Sobolevskyi R., Korobiichuk V., Levytskyi V. et al. Optimization of the process of efficiency management of the primary kaolin excavation on the curved face of the conditioned area // Rudarsko-geološko-naftni zbornik. 2020. Vol. 35. № 1.123-138. DOI: 10.17794/rgn.2020.1.10
Klanfar M., Herceg V., Kuhinek D., Sekulić K. Construction and testing of the measurement system for excavator productivity // Rudarsko-geološko-naftni zbornik. 2019. Vol. № 2. P.51-58. DOI: 10.17794/rgn.2019.2.6
Cheol-Gyu Park, Seungjin Yoo, Hyeonsik Ahn et al. A coupled hydraulic and mechanical system simulation for hydraulic excavators // Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering 2019. Vol. Iss. 4. P. 527-549. DOI: 10.1177/0959651819861612
Ng F., Harding A.J., Glass J. An eco-approach to optimise efficiency and productivity of a hydraulic excavator // Journal of Cleaner Production. 2016. Vol. 112. Part 5. P. 3966-3976. DOI: 10.1016/j.jclepro.2015.06.110
Juraev A. Study of the Effect of Hydraulic Systems Operation on the General Performance of a Hydraulic Excavator // The American Journal of Engineering and Technology. 2021. Vol. 3. Iss. 10. P. 36-42. DOI: 10.37547/tajet/Volume03Issue10-07

Оценка влияния температуры рабочей жидкости на потери мощности карьерного гидравлического экскаватора

Аннотация

Введение

Методы

Значения коэффициентов для рабочей жидкости Shell Tellus S2 V 46

Исходные параметры для моделирования

Обсуждение результатов

Потери мощности в процессе выполнения рабочих операций, кВт

Значения диапазона температур при различной вязкости рабочих жидкостей

Литература

Похожие статьи