Изучение механизма тонкослойной сушки и диффузии низкосортного угля Внутренней Монголии и провинции Юньнань
- 1 — магистр, магистр технологии обогащения полезных ископаемых Горно-технологический факультет химического машиностроения Китайского университета ▪ Orcid
- 2 — док. наук канд. техн. наук в области обогащения полезных ископаемых Горно-технологический факультет химического машиностроения Китайского университета ▪ Elibrary
- 3 — док. наук доцент Лаборатория переработки угля и эффективного чистого использования Министерства образования, Китайский горно-технологический университет ▪ Orcid
- 4 — док. наук профессор Лаборатория переработки угля и эффективного чистого использования Министерства образования, Китайский горно-технологический университет ▪ Orcid
- 5 — док. наук доцент Лаборатория переработки угля и эффективного чистого использования Министерства образования, Китайский горно-технологический университет ▪ Orcid
Аннотация
Китай богат угольными ресурсами, на долю которых приходится более 90 % всех установленных запасов ископаемого топлива, при этом доля потребления угольной энергии достигла в 2021 г. 56,5 %. В качестве объекта исследования был выбран низкосортный уголь, поступающий из Внутренней Монголии (образцы NM) и провинции Юньнань (образцы YN). Характеристики потери массы образцов были изучены с использованием термогравиметрического анализа для определения подходящей температуры для экспериментов по сушке, поскольку высокая влажность низкосортного угля может легко вызвать остановку оборудования в процессе сухой сортировки. Эксперименты по тонкослойной сушке проводились при различных температурных условиях. Эффективный коэффициент диффузии влаги подбиралcя по уравнению Аррениуса, для образцов NM он составил 5,07·10–11 - 9,58·10–11 м2/с; для трех разных размеров частиц образцов YN – 1,89·10–11 - 4,92·10–11 (крупность –1 мм), 1,38·10–10 - 4,13·10–10 (крупность 1-3 мм), 5,26·10–10 - 1,49·10–9 (крупность 3-6 мм). Энергия активации образцов из Внутренней Монголии составила 10,97 кДж/моль (крупность –1 мм); для образцов из провинции Юньнань – 17,97 кДж/моль (крупность –1 мм), 33,52 кДж/моль (крупность 1-3 мм) и 38,64 кДж/моль (крупность 3-6 мм). Процесс сушки был смоделирован по эмпирическим и полуэмпирическим формулам. Установлено, что оптимальными моделями для образцов Внутренней Монголии является двухкомпонентная модель диффузии, а для образцов из провинции Юньнань – уравнение Hii.
Финансирование
Исследовательская работа финансируется Национальным фондом Китая для выдающихся молодых ученых (№ 52125403), Фондом естественных наук провинции Цзянсу (№ BK20200651), Национальным фондом естественных наук Китая (№ 52104276, № 52261135540, № 52220105008), Международной программой стипендий по обмену сотрудников с ученой степенью (№ PC2021086), Инновационной программой для выпускников Китайского горно-технологического университета (№ 2022WLJCRCZL057), Инновационной программой последипломных исследований и практики провинции Цзянсу (№ SJCX22_1149).
Введение
Уголь является одним из важнейших энергоносителей в мире и способствует экономическому и социальному развитию [1]. Угольные ресурсы Китая составляют более 90 % установленных запасов всех ископаемых источников энергии, при этом доля низкосортного бурого угля – около 40 % [2, 3]. Низкосортный уголь обладает низкой степенью углефикации, высокой влажностью, большим количеством кислородсодержащих функциональных групп, а легкое выветривание и самовозгорание препятствуют его разработке и использованию [4]. Высокая влажность не только ограничивает теплотворную способность сжигания низкосортного угля, но и увеличивает стоимость транспортировки. Кроме того, низкосортный уголь размером менее 6 мм легко вызывает засорение оборудования в процессе сухой подготовки, что стало серьезной технической проблемой при сухом обогащении [5]. Таким образом, обезвоживание низкосортных углей имеет большое стратегическое значение [6].
Исследование критериев текучести в работе Yong Jin et al. [7] показали, что она снижается с увеличением содержания влаги, при этом отмечено, что текучесть и уплотняющие свойства различаются как выше, так и ниже критической влажности. Эксперименты с низкотемпературной сушкой Xian Wu et al. [8] показали, что существует промежуток времени между усадкой объема и потерей воды, а также имеются различия в их количествах. Rongtang Liu et al. [9] в ходе экспериментов по сушке иминьского бурого угля при различных температурах обнаружили, что при низких температурах образуются только H2O и CO2. Горючие газы, включая CO и химические газы, могут образовываться, когда температура сушки превышает 250 °C. B.A.Fu и M.Q.Chen [10] экспериментально исследовали кинетику тонких слоев бурого угля при принудительной конвективной сушке горячим воздухом, результаты показали, что процесс сушки представляет собой комбинацию двух коротких периодов – падения скорости. H.Zhou et al. [11] исследовали влияние содержания влаги на плотнофазное пневмотранспортирование пылевидного бурого угля под высоким давлением. Установлено, что при сильной межчастичной когезии частицы подвергаются серьезной агломерации, что приводит к увеличению сил сопротивления, плохому псевдоожижению или даже полной дефлюидизации при псевдоожижении. P.Celen et al. [12] высушивали турецкий бурый уголь с использованием перегретого пара и горячего воздуха при температуре 117 °C. Эксперименты показали, что на нагрев образцов лигнита перегретым паром уходит меньше времени, чем на нагрев горячим воздухом. B.A.Fu et al. [13] изучали теплообмен в тонких слоях бурого угля при конвективной сушке горячим воздухом. В результате были установлены зависимости влияния температуры и скорости горячего воздуха на температуру тонкого слоя.
В исследовательских работах недостаточно изучен механизм сушки и факторной оценки низкосортных углей крупностью менее 6 мм. В данной работе будет исследовано влияние температуры, размера частиц, органического состава и содержания влаги на характеристики сушки низкосортного угля, а также методом кинетического анализа будет проанализирован механизм воздействия различных факторов на процесс сушки. Также в статье представлены данные и практические рекомендации для решения технических проблем сушки трудноклассифицируемого низкосортного угля крупностью менее 6 мм [14].
Методы
Для решения указанных технических проблем в качестве объектов в статье использовался низкосортный уголь из провинций Чжаотун, Юньнань (YN), Шэнли, Внутренняя Монголия (NM). Образцы YN были раздроблены с последующим просевом для отбора образцов до размера частиц –1, 1-3 и 3-6 мм. Образцы NM были раздроблены до крупности –1 мм.
Для понимания основных физических параметров и характеристик экспериментальные образцы были подвергнуты промышленному и элементному анализам с использованием автоматического промышленного анализатора TGA701 производства Deco (США) и элементного анализатора Elementar Vario MACRO cube (Германия).
Перед сушкой образцы подвергались термогравиметрическому анализу для определения подходящей температуры сушки. Анализ проводился с использованием термогравиметрического (термического) дифференциального анализатора TG фирмы NETZSCH (Германия). Масса образца для проведения анализа составляла около 12 мг, материал загружался в пустой тигель и продувался воздухом со скоростью потока 50 мл/мин. Повышение температуры поддерживалось со скоростью 10 °С/мин, а абсолютную температуру регулировали на уровне 800 °С.
Образцы сушились в доменной печи модели 101A-1ET производства Шанхайской фабрики экспериментальных инструментов в специальном алюминиевый лотке размерами 27 x 20 x 2 см. Измерения проводились с помощью электронных весов Sartorius BSA 224S (Германия) с точностью до 0,0001 г. Для минимизации ошибки теста лоток был накрыт оловянной фольгой во избежание экстремальных температур, вызывающих прилипание низкосортного угля и коррозию лотка органическими веществами, а образец распределен тонким слоем. Отслеживалось время сушки и изменение качества образца до тех пор, пока он не высыхал до постоянной массы. Образцы просушивались при скорости сушильного агента 0,6 м/с. Для каждого теста отбирался образец массой 10 г и сушился до постоянной массы. В наблюдениях за изменением органического состава образца до и после сушки в данной работе использовалось инфракрасное тестирование для идентификации функциональных групп образца [15]. Для каждого времени рассчитывались влажность и скорость сушки и строилась кривая сушки [16, 17]:
- влажность сухой основы
- скорость сушки
где m – масса образца для каждого испытания, г; n – масса образца при высушивании до постоянной массы, г.
Частицы пористых сред в основном находились в тонком слое в процессе изотермической сушки. Кинетическая энергия молекул воды обеспечивалась градиентом температуры. Градиент концентрации был основной движущей силой в процессе миграции молекул воды. Концентрация вещества зависела от продолжительности диффузии. Следовательно, процесс сушки низкосортного угля можно описать вторым законом Фика [18-21]:
где Mt – содержание воды в испытуемом образце в момент времени t, г/г; Deff – эффективный коэффициент диффузии влаги, м2/с.
Для обработки данных использовалось приближение второго порядка второго закона диффузии Фика с аналитическим решением [22, 23]:
где L – толщина тонкого слоя образца в лотке (в данном исследовании L = 0,002 м); MR – содержание воды по массе, %.
Содержание воды по массе рассчитывалось по следующей формуле [24]:
где М0 – начальная влажность, %; Me – содержание воды в равновесном состоянии, %.
Поскольку Me пренебрежимо мало по сравнению с M0 уравнение (2) можно упростить [25, 26]:
Эффективный коэффициент диффузии влаги пористых частиц зависит от состава материала частиц, влаги и природы самого материала. Его связь с температурой подчиняется уравнению Аррениуса [27]:
Логарифмирование обеих частей уравнения Аррениуса дает следующее равенство [26]:
где D0 определяется материалом, м2/с; Ea – энергия активации, Дж/моль; R – газовая постоянная, Дж/(моль/K); Т – температура сушильной среды, K.
Исследователи считают, что сушка представляет собой неустановившийся процесс тепломассопереноса и тепломассообмена, поэтому часто используются методы подбора ее адекватной модели [28]. В настоящее время большинство моделей, использующихся в областях сушки пищевых продуктов и материалов, могут быть применены и для сушки низкосортной углей [29, 30]. В данном исследовании для подбора рассматриваются 16 классических моделей сушки, которые широко используются в исследованиях тонкослойной сушки, включая теоретические, эмпирические, полуэмпирические модели и т.д. В качестве показателя оценки используется коэффициент корреляции [31]:
где yi – экспериментальное значение; Yi – теоретически рассчитанное значение подогнанной кривой; n – количество экспериментальных значений.
Чем ближе коэффициент R2 к 1, тем лучше эффект подгонки.
Отобранные 16 теоретических, эмпирических и полуэмпирических моделей сушки, использованных при моделировании подгонки, показаны в табл.1. Среди них теоретическая модель получена из теории, связанной с сушкой (включая дифференциальное уравнение диффузии влаги, тепловое уравнение электропроводности и др.), тогда как полуэмпирическая модель устанавливается путем объединения кинетических экспериментальных данных с высокой точностью, а эмпирическая модель, построенная на основе экспериментальных данных, может точно описать зависимость между влажностью материала и временем сушки [32].
В настоящее время проведена большая исследовательская работа по моделированию оборудования для сушки угля низкого качества, и результаты показывают, что теоретическая модель дает менее точный прогноз, чем эмпирическая и полуэмпирическая модели. Тем не менее, эмпирическая или полуэмпирическая модели не могут раскрыть теоретические аспекты механизма массо- и теплопереноса в процессе сушки. Следовательно, в данной работе предпочтение отдается теоретической модели как наиболее подходящей, а затем из базовой теории раскрывается механизм сушки.
Таблица 1
Математические модели сушки
|
Тип |
Название |
Автор |
Формулы |
|
Теоретическая |
Одиночная диффузия |
Хендерсон и Пабис |
формула
|
|
Двухчленная диффузия |
Шараф-Элдин |
формула
|
|
|
Трехчленная диффузия |
Каратанос |
формула
|
|
|
Полуэмпирическое уравнение |
Модель Лемуса |
Лемус |
формула
|
|
Модель Льюиса |
Льюис |
формула
|
|
|
Логарифмическая |
Тогрул и Пехилван |
формула
|
|
|
Модель Пейджа |
Пейдж |
формула
|
|
|
Уточненная модель Пейджа I |
Оверхулс |
формула
|
|
|
Уточненная модель Пейджа II |
Ван |
формула
|
|
|
Модель Hii |
Hii |
формула
|
|
|
Приблизительная диффузия |
Ялдыз |
формула
|
|
|
Модель Вема |
Вема |
формула
|
|
|
Эмпирические уравнения |
Модель Чандра |
Чандра |
формула
|
|
Модель Мидилли |
Мидилли |
формула
|
|
|
Модель Томпсона |
Томпсон |
формула
|
|
|
Модель Вана |
Ван |
формула
|
Результаты и обсуждение
В табл.2 представлены результаты испытаний физических свойств образцов из Внутренней Монголии (NM) и провинции Юньнань (YN), влажность образцов составила 41,90 и 21,61 % соответственно. Кроме того, содержание углерода в образце из Внутренней Монголии было значительно выше, чем в образце из Юньнани, в нем содержалось больше органических элементов, и он имел более низкую степень углефикации.
Таблица 2
Промышленный и элементный анализы бурых углей Внутренней Монголии, %
|
Образец |
Промышленный анализ |
Элементный анализ |
|||||||||
|
Mad |
Ad |
Vad |
Aad |
Fcad |
Cdaf |
Hdaf |
Odaf |
Ndaf |
Sdaf |
||
|
NM |
41,90 |
32,11 |
37,55 |
27,27 |
20,12 |
56,41 |
4,56 |
37,44 |
0,83 |
0,76 |
|
|
YN |
21,62 |
11,49 |
26,74 |
7,63 |
32,01 |
40,13 |
3,15 |
57,80 |
1,35 |
1,57 |
|
Примечание: Mad, Ad, Vad, Aad и Fcad относятся к содержанию влаги, летучих веществ, связанного углерода и золы в пересчете на полученную сухую массу; Hdaf, Ndaf, Odaf и Sdaf относятся к содержанию элементов в пересчете на сухую беззольную массу.
Дифференциальные термогравиметрические кривые (ДТГ) и термогравиметрические кривые (ТГ) образцов, построенные по данным термогравиметрического эксперимента, представлены на рис.1. Кривые ТГ и ДТГ образцов YN и NM можно разделить на три этапа. Cтадия водоотдачи образцов NM находится в интервале температур 75-200 °С. Фаза потери массы с органическим веществом находится в интервале температур 500-750 °С. Стадия потери массы и самовозгорания наступала после 750 °С. Стадия потери массы от влаги образцов YN составляла 85-220 °С. Фаза потери массы с органическим веществом составляла 450-750 °С, а фаза потери массы с самовозгоранием наступала после 750 °С. Это можно объяснить тем, что испарение свободной и связанной воды в угле завершается при 220 °С, а большая часть этой воды испаряется при 100 °C. При продолжающемся повышении температуры улетучивание органического вещества в угле происходит при 250 °С, сам же уголь подвергается самовозгоранию при температуре 750 °C [33].
Результаты экспериментов с образцами NM показали, что время сушки образцов при 180 °С составило 6 мин; при 160 °С – 7 мин; при 140 °С – 9 мин; при температуре ниже 140 °С – более 10 мин (рис.2). Это связано с тем, что чем выше температура горячего воздуха, тем выше температура образца, и тем больше кинетическая энергия молекул воды внутри частиц, что ускоряет процесс диффузии воды. В то же время скорость испарения воды на поверхности частиц увеличивается, что увеличивает градиент концентрации между поверхностью и внутренней влагой частиц, так что жидкая фаза мигрирует к поверхности с большей скоростью.
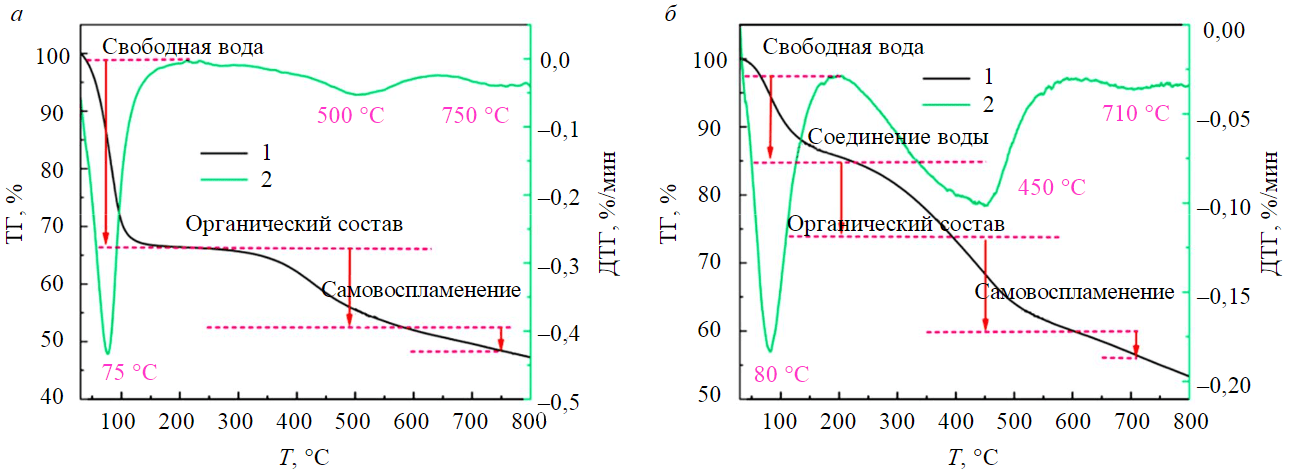
Рис.1. Термогравиметрические кривые образцов – NM (a) и YN (б) 1 – ТГ; 2 – ДТГ
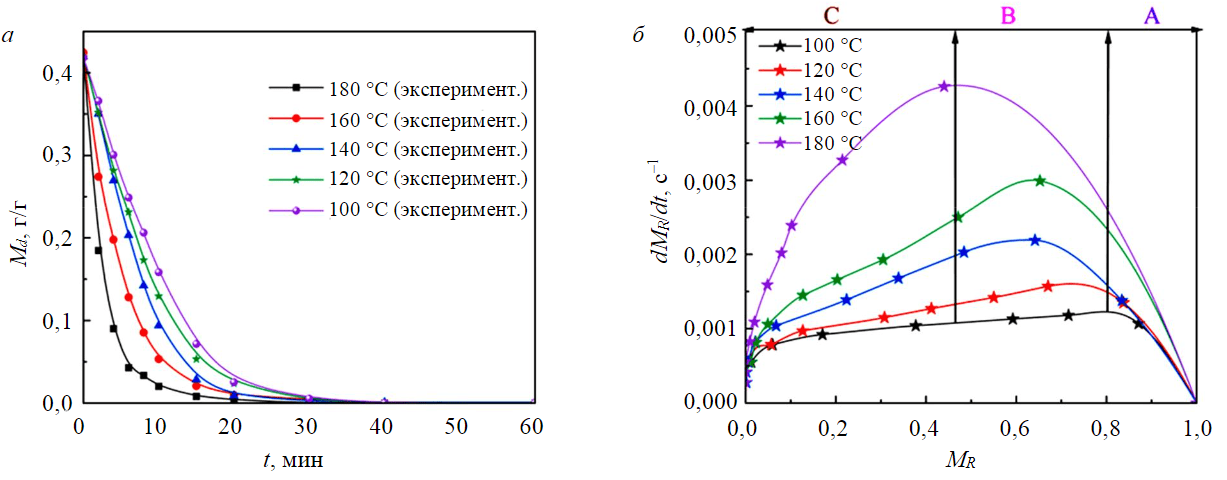
Рис.2. Кривые сушки (а) и скорости сушки (б) образцов NM размером –1 мм при различных температурах
При температуре сушки более 160 °C повышение температуры дает меньший эффект. Кроме того, чем выше температура сушки, тем выше максимальная скорость и больше продолжительность стадии замедленной сушки.
При более низких температурах период сушки с постоянной скоростью был более выраженным. Это объясняется тем, что большее количество тепла, приносимое высокой температурой, заставляет свободную воду быстрее испаряться за меньший срок, а для поглощения тепла при сушке на низких температурах требуется определенное время, поэтому скорость испарения свободной воды находится в более сбалансированном состоянии [34].
Как показано на рис.3, при температуре сушки выше 140 °C время завершения сушки образцов YN (–1 мм) составляет около 15 мин; при температуре сушки ниже 140 °C – около 20 мин. Вместе с тем при высоком содержании органической составляющей эффективность сушки образца снижается. При температуре менее 140 °С разница в процессе сушки образцов YN невелика. При температуре выше 140 °С разрыв в первые десять минут увеличивается. Из этого следует, что органические компоненты начинают существенно влиять на процесс, когда температура сушки превышает 140 °С.
На кривых скорости сушки при разных температурах образцов YN присутствуют только стадии разгона и торможения. Фазу увеличения скорости можно рассматривать как период, в течение которого начальная скорость быстро достигает максимума. Это связано с тем, что изначально существовала большая разница температур между образцом и сухим горячим воздухом, и по мере протекания процесса разница температур становится все меньше, а эффективность теплопередачи между горячим воздухом и частицей постепенно снижается. В это время содержание воды в образце также быстро уменьшается из-за быстрого испарения свободной влаги, а оставшаяся влага считалась внутренней влагой частиц образца. Эта влага должна была быть сначала отделена от в вещества частиц теплом, а затем перенесена на поверхность частиц. Стадия сушки после достижения максимума на рис.3, б иллюстрирует увеличение сопротивления теплопередаче при испарении внутренней влаги.
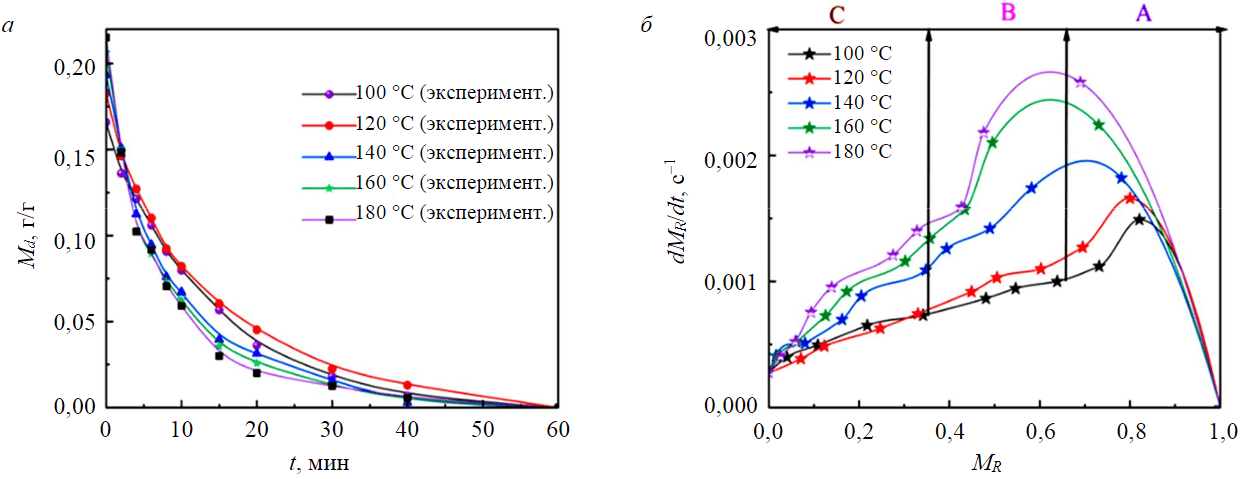
Рис.3. Кривые сушки (а) и скорости сушки (б) образцов YN размером –1 мм при различных температурах
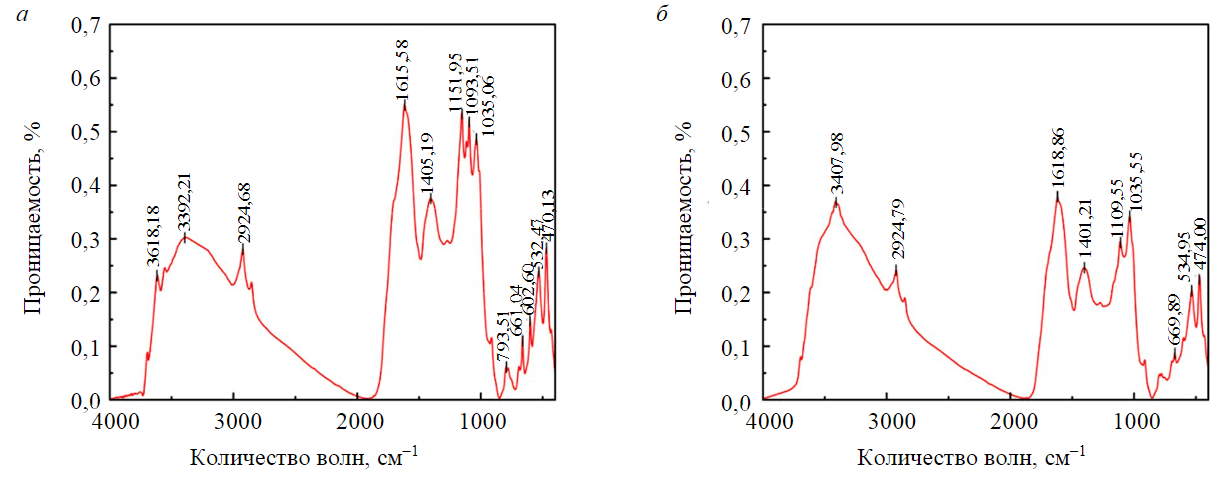
Рис.4. Кривые сушки и скорости сушки образцов YN до (a) и после (б) высыхания
В экспериментальных результатах разница равновесной влажности составляла 3-6 % при различных температурах в течение 60 мин. Это происходило потому, что образец YN содержит больше элементов S, N и O и больше органического вещества, поэтому чем выше температура сушки, тем больше улетучиваются компоненты в образце YN, и тем больше теряется масса. Чтобы продемонстрировать это, был проведен инфракрасный анализ образцов YN до и после сушки (рис.4).
Инфракрасный анализ показал, что образец был богат органическими функциональными группами, такими как OH–, –CO–, –CH, –SO–, –N=O перед сушкой. Однако после сушки органические функциональные группы, такие как ОН–, СО, СН, SO, N=O, значительно сократились или даже исчезли. Это показывает, что органические компоненты не только снижают эффективность сушки, но и увеличивают погрешность эксперимента за счет термического разложения и улетучивания.
При температуре сушки ниже 140 °С время завершения сушки образцов крупностью –1 мм было значительно меньше, чем у образцов крупностью 1-3 мм (рис.5) и 3-6 мм (рис.6), разница во времени завершения сушки между образцами 1-3 и 3-6 мм была незначительной. Когда температура сушки превышала 140 °C, время завершения сушки образцов крупностью –1 мм было значительно меньше, чем образцов размером 1-3 мм, а время окончания сушки образцов крупностью 1-3 мм настало значительно быстрее, чем образцов крупностью 3-6 мм. Это происходило потому, что чем меньше частицы, тем легче молекулам воды поглощать тепло и испаряться. В процессе средне- и низкотемпературной сушки движущая сила молекул воды в основном определялась градиентом концентрации, причем ведущую роль играл механизм диффузии. Когда температура сушки была выше, температурное поле могло обеспечивать большую кинетическую энергию для миграции молекул воды.
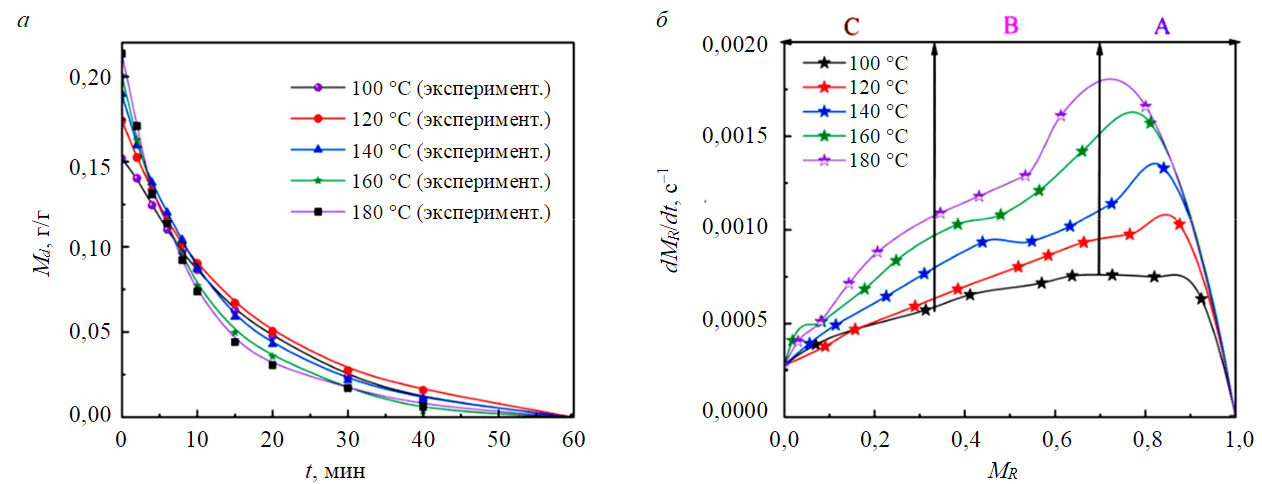
Рис.5. Процесс сушки (а) и кривая скорости сушки (б) образцов YN размером 1-3 мм при различных температурах
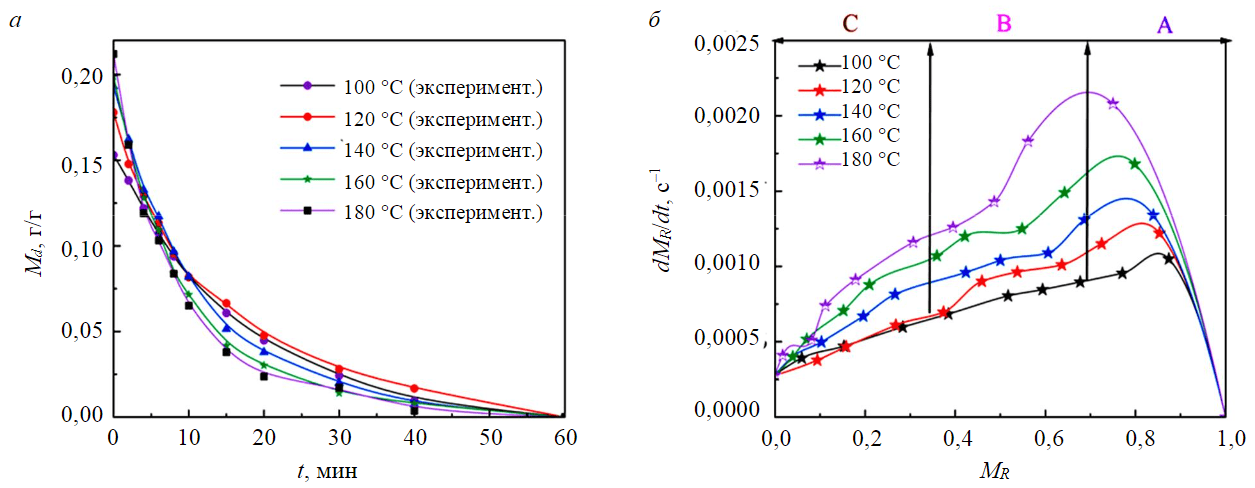
Рис.6. Процесс сушки (а) и кривая скорости сушки (б) образцов YN размером 3-6 мм при различных температурах
Для количественной оценки завершения сушки каждого образца результаты экспериментов по сушке были проанализированы кинетически. Результаты экспериментов по изотермической сушке выведены в соответствии с уравнением (1). Была получена кривая зависимости lnMR низкосортного угля при соответствующей температуре от времени t. Параметр Deff при соответствующей температуре определялся по наклону кривой (табл.3).
Таблица 3
Эффективный коэффициент диффузии влаги Deff при различных температурах сушки, м2/с
|
Образец |
Температура сушки, °С |
||||
|
100 |
120 |
140 |
160 |
180 |
|
|
NM –1 мм |
5,07∙10–11 |
6,19∙10–11 |
7,56∙10–11 |
8,14∙10–11 |
9,58∙10–11 |
|
R2 |
0,98647 |
0,98741 |
0,99101 |
0,99706 |
0,95812 |
|
YN –1 мм |
1,89∙10–11 |
2,11∙10–11 |
2,97∙10–11 |
4,49∙10–11 |
4,92∙10–11 |
|
R2 |
0,99373 |
0,97746 |
0,96129 |
0,96738 |
0,98684 |
|
YN 1-3 мм |
1,38∙10–10 |
1,76∙10–10 |
2,53∙10–10 |
3,08∙10–10 |
4,13∙10–10 |
|
R2 |
0,99324 |
0,97819 |
0,99200 |
0,98756 |
0,99626 |
|
YN 3-6 мм |
5,26∙10–10 |
6,59∙10–10 |
8,92∙10–10 |
1,13∙10–9 |
1,49∙10–9 |
|
R2 |
0,96331 |
0,98591 |
0,99429 |
0,98304 |
0,98968 |
При одном и том же размере частиц в миллиметрах эффективный коэффициент диффузии воды для образцов NM составил 5,07·10–11-9,58·10–11 м2/с. Эффективный коэффициент диффузии воды образцов YN был небольшим и составлял 1,89·10–11-4,92·10–11 м2/с. Сравнительный анализ показывает, что эффективный коэффициент диффузии влаги увеличивается с повышением температуры сушки, поскольку чем выше температура, тем больше кинетическая энергия молекул воды и тем сильнее способность к диффузии. При этом чем больше размер частиц, тем больше эффективный коэффициент диффузии влаги – эффективный коэффициент диффузии воды образца YN (крупность 1-3 мм) составил 1,38·10–10-4,13·10–10 м2/с, образца YN (крупность 3-6 мм) 5,26·10–10-1,49·10–9 м2/с. Это объясняется тем, что размер частиц является важным параметром положительной корреляции, влияющим на эффективный коэффициент диффузии влаги в эмпирическом уравнении. Кроме того, при диффузии молекул воды чем больше размер частиц, тем больше каналов диффундируют молекулы воды и тем больше влаги испаряется в единицу времени. Однако эффективный коэффициент диффузии воды на единицу размера частиц будет уменьшаться, поскольку чем больше размер частиц, тем длиннее путь диффузии воды, что снижает эффективность диффузии.
Видимая энергия активации является важным параметром кинетики сушки, отражающим ее сложность. В результате исследования были проанализированы характеристики сушки низкосортных углей путем сравнения видимой энергии активации низкосортных углей с различной влажностью и размером частиц. Видимая энергия активации была рассчитана путем подгонки эффективного коэффициента диффузии воды (табл.4). Видимая энергия активации образцов NM составила 10,97 кДж/моль, что ниже, чем у образцов YN (17,97 кДж/моль). Видимая энергия активации образцов YN положительно соотносилась с размером частиц и составляла 18,95 и 20,28 кДж/моль для размеров 1-3 и 3-6 мм соответственно. Результаты подгонки показывают, что чем выше содержимое влаги в образце, тем ниже видимая энергия активации. Это является следствием того, что чем выше содержание влаги в образце, тем сильнее движущая сила, обеспечиваемая градиентом концентрации влаги и тем меньше энергии требуется для диффузии внутренней влаги. Чем больше размер частиц, тем больше видимая энергия активации, так как длиннее путь диффузии влаги наружу [35-39].
Таблица 4
Значения видимой энергии активации образцов угля в испытании
|
Образец |
Еа, кДж/моль |
Т, К |
Размер, мм |
Md, % |
|
NM |
10,97 |
373θi453 |
–1 мм |
41,90 |
|
YN |
17,97 |
373i453 |
–1 мм |
21,36 |
|
YN |
18,95 |
373i453 |
1-3 мм |
21,36 |
|
YN |
20,28 |
373i453 |
3-6 мм |
21,36 |
Экспериментальные данные каждого образца были проанализированы с использованием 16 уравнений (табл.5) для получения оптимальной кинематической модели сушки. Лучшая модель для каждого образца была подобрана для пяти различных условий работы, а данные испытаний для каждого условия работы были получены путем усреднения шести наборов одних и тех же испытаний. Наилучшей моделью для образцов NM размером –1 мм была определена двухкомпонентная модель диффузии, а для образцов YN с различными размерами частиц стало уравнение Hii. Параметры результатов подгонки представлены в табл.5.
Эксперименты показали хороший результат подгонки: параметр R2 для образцов YN класса –1 мм при 100, 120, 140, 160, 180 °С равен 0,9984, 0,9994, 0,9987, 0,9976, 0,9971 соответственно; для класса 1-3 мм при 100, 120, 140С, 160, 180 °С R2 равен 0,9989, 0,9993, 0,9976, 0,9991, 0,9982 соответственно; для класса 3-6 мм при 100, 120, 140, 160 и 180 °С R2 равен 0,9989, 0,9993, 0,9976, 0,9991, 0,9982 соответственно (рис.7).
Таким образом было установлено, что двухкомпонентная модель диффузии подходит для моделирования образцов с высоким содержанием влаги, а модель Hii – для моделирования образцов с низким содержанием влаги. Установлено, что механизм диффузии, управляемый градиентом концентрации, играет доминирующую роль в образцах с высоким содержанием влаги. Двухкомпонентная модель диффузии может хорошо предсказать изотермическую картину тонкослойной сушки образцов с высоким содержанием влаги. Для образцов с низким содержанием влаги градиент концентрации также был одной из движущих сил, но не доминирующей, поэтому диффузионная модель не применима к образцам с низким содержанием влаги.
Таблица 5
Подгонка результатов каждого образца
|
Образцы |
Модель |
Размер, мм |
Температура, °С |
R2 |
а1 |
а2 |
k1 |
k2 |
n |
|
YN |
Hii |
–1 |
100 |
0,9984 |
–0,2588 |
0,4186 |
0,1236 |
0,1075 |
00,8932 |
|
120 |
0,9994 |
0,0148 |
0,1699 |
10,6822 |
0,0793 |
0,9502 |
|||
|
140 |
0,9976 |
–1,0517 |
1,2452 |
0,6375 |
0,5431 |
0,5707 |
|||
|
160 |
0,9987 |
–0,2042 |
0,4004 |
0,3874 |
0,7343 |
0,4558 |
|||
|
180 |
0,9971 |
–0,1303 |
0,3414 |
0,7614 |
0,3398 |
0,6853 |
|||
|
YN |
Hii |
1-3 |
100 |
0,9989 |
–0,0061 |
0,1581 |
0,1257 |
0,0688 |
0,9843 |
|
120 |
0,9993 |
0,0078 |
0,1701 |
0,3591 |
0,0661 |
10,0437 |
|||
|
140 |
0,9976 |
–0,1059 |
0,2992 |
0,6649 |
0,2652 |
0,7599 |
|||
|
160 |
0,9991 |
–0,0857 |
0,2847 |
10,0299 |
0,3042 |
0,6759 |
|||
|
180 |
0,9982 |
0,0218 |
0,1903 |
20,972 |
0,1006 |
10,0741 |
|||
|
YN |
Hii |
3-6 |
100 |
0,9992 |
0,0594 |
0,0915 |
0,0949 |
0,0422 |
1,1440 |
|
120 |
0,9977 |
–3,1667 |
3,3309 |
0,3277 |
0,3126 |
0,7225 |
|||
|
140 |
0,9987 |
–0,0971 |
0,2748 |
0,3509 |
0,1531 |
0,8548 |
|||
|
160 |
0,9958 |
–0,1361 |
0,3264 |
0,9158 |
0,3228 |
0,6994 |
|||
|
180 |
0,9989 |
0,2184 |
–0,0048 |
0,1398 |
329,05 |
0,8481 |
|||
|
NM |
Двухкомпонентная модель диффузии |
–1 |
100 |
0,9986 |
–5,8756 |
6,2918 |
0,1955 |
0,1855 |
– |
|
120 |
0,9994 |
–18,929 |
19,345 |
0,2087 |
0,2055 |
– |
|||
|
140 |
0,9976 |
–3,1762 |
30,5939 |
0,2474 |
0,2253 |
– |
|||
|
160 |
0,9966 |
–6,9891 |
7,4073 |
0,2595 |
0,2517 |
– |
|||
|
180 |
0,9994 |
0,3651 |
0,0582 |
0,4969 |
0,1226 |
– |
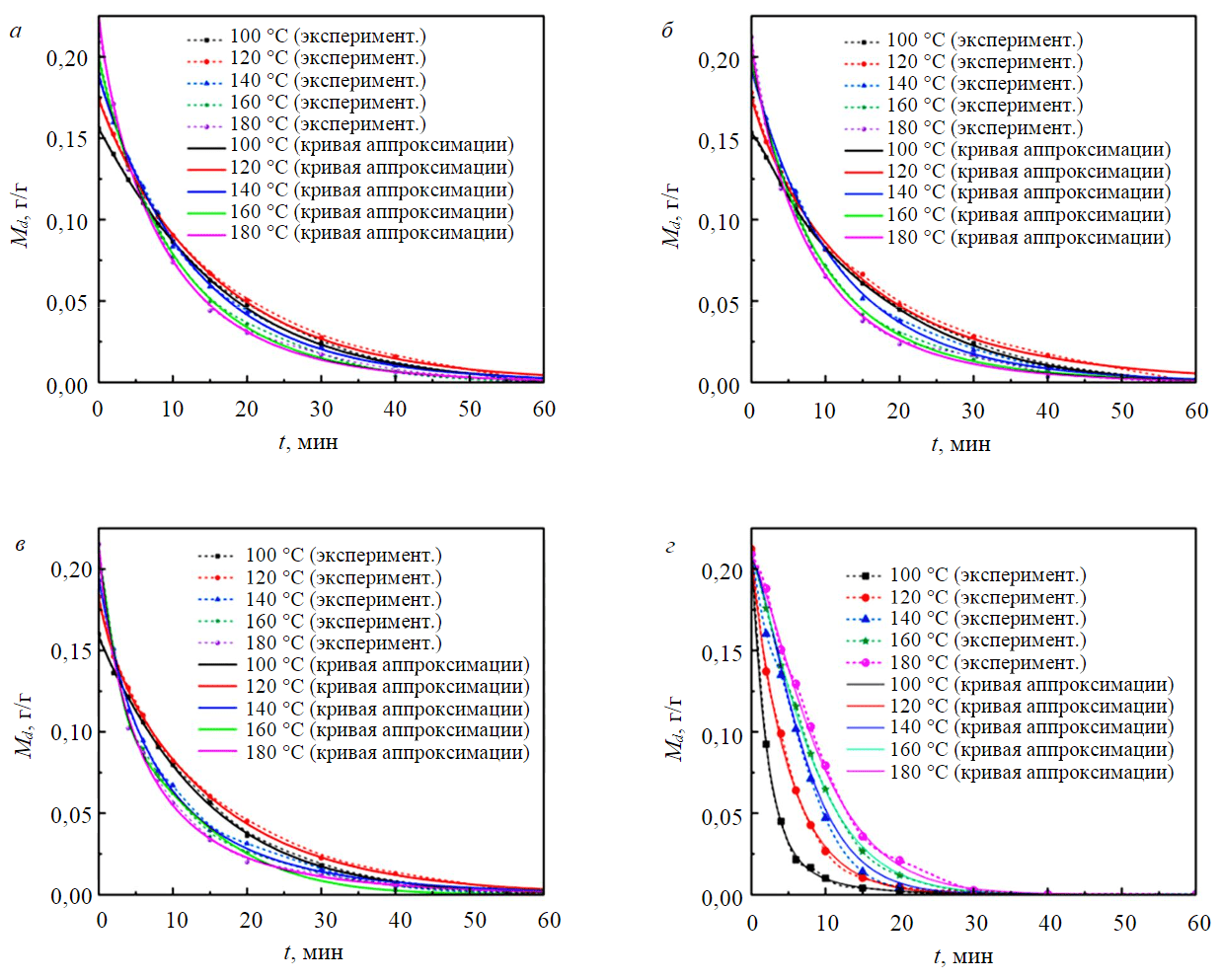
Рис.7. Анализ подгонки результатов экспериментов на образцах YN класса 3-6 мм (а); YN класса 1-3 мм (б); YN класса –1 мм (в); NM класса –1 мм (г) при различных температурах
Заключение
В данной статье представлены результаты экспериментов – по тонкослойной изотермической сушке на образцах низкосортных углей и анализ данных, полученных в ходе экспериментов. Были построены кривые скорости сушки, определены эффективный коэффициент диффузии влаги и видимая энергия активации каждого образца. Экспериментальные данные сопоставлялись с 16 математическими моделями сушки, и для каждого образца была выбрана наиболее подходящая модель сушки. Выводы данной работы показывают следующие результаты:
- Влажность и температура являются двумя наиболее важными факторами, влияющими на процесс сушки. Для образцов NM при температуре менее 140 °С кривая скорости сушки имеет три стадии: роста, устойчивости и спада. При температуре выше 140 °С кривая сушки имеет только две стадии: роста и спада. Для образцов YN трех разных размеров отмечено наличие только двух стадий сушки при 100-180 °С: роста и спада. Когда температура превышает 160 °C для образцов YN и 140 °C для образцов NM, повышение температуры больше не оказывает значительного воздействия на эффективность сушки образцов. Кроме того, чем меньше размер частиц, тем выше эффективность сушки, а повышение температуры усиливает влияние размера частиц на эффективность сушки. Органические компоненты также снижают эффективность сушки и улетучиваются при высоких температурах на более поздних стадиях сушки.
- Чем выше влажность образца, тем больше эффективный коэффициент диффузии воды. Чем больше размер частиц, тем выше эффективный коэффициент влажности и тем меньше эффективный коэффициент влажности на единицу диаметра. Чем выше температура, тем больше эффективный коэффициент диффузии влаги. В то же время видимая энергия активации образцов с низким содержимым влаги выше и повышается с увеличением размера частиц. Кроме того, образцы NM адекватно описываются двухпараметрической моделью диффузии, а три образца YN с разными размерами частиц соответствуют уравнению Hii.
- При анализе влияющих факторов было установлено, что влажность оказывает наибольшее влияние на процесс сушки. Вторым по воздействию на процесс фактором является температура. Когда температура достигает определенного значения, ее дальнейшее повышение не оказывает существенного влияния на эффективность сушки. Третьим фактором влияния на процесс сушки был размер частиц. В низкосортных углях эффект сушки образца –1 мм был наилучшим. Четвертый фактор – содержание органических компонентов, которые не только снижают эффективность сушки, но и увеличивают потерю массы при улетучивании.
На следующем этапе исследования планируется дополнительно выявить механизм сушки низкосортного угля с помощью методов численного моделирования и проанализировать механизм массо- и теплопереноса процесса сушки в мезоскопическом масштабе.Аркадий Бабченко
Литература
- Aleksandrova T., Nikolaeva N., Kuznetsov V. Thermodynamic and Experimental Substantiation of the Possibility of Formation and Extraction of Organometallic Compounds as Indicators of Deep Naphthogenesis // Energies. 2023. Vol. 16. Iss. 9. № 3862. DOI: 10.3390/en16093862
- Capellán-Pérez I., Mediavilla M., de Castro C. et al. Fossil fuel depletion and socio-economic scenarios: An integrated approach // Energy. 2014. Vol. 77. P. 641-666. DOI: 10.1016/j.energy.2014.09.063
- Shunxuan Hu, Junguo Li, Xin Yang et al. Improvement on slurry ability and combustion dynamics of low quality coals with ultra-high ash content // Chemical Engineering Research and Design. 2020. Vol. 156. P. 391-401. DOI: 10.1016/j.cherd.2020.02.011
- Александрова Т.Н., Кусков В.Б., Афанасова А.В., Кузнецов В.В. Совершенствование технологии флотационного обогащения тонких классов коксующихся углей // Обогащение руд. 2021. № 3. С. 9-13. DOI: 10.17580/or.2021.03.02
- Chenyang Zhou, Xuchen Fan, Chenlong Duan, Yuemin Zhao. A method to improve fluidization quality in gas–solid fluidized bed for fine coal beneficiation // Particuology. 2019. Vol. 43. P. 181-192. DOI: 10.1016/j.partic.2017.12.012
- Daegi Kim, Seyong Park, Ki Young Park. Upgrading the fuel properties of sludge and low rank coal mixed fuel through hydrothermal carbonization // Energy. 2017. Vol. 141. P. 598-602. DOI: 10.1016/j.energy.2017.09.113
- Yong Jin, Haifeng Lu, Xiaolei Guo, Xin Gong. Effect of water addition on flow properties of lignite particles // Chemical Engineering Research and Design. 2018. Vol. 132. P. 1020-1029. DOI: 10.1016/j.cherd.2017.11.012
- Wu Xian, Dong Ziwen, Sun Lifeng, Jia Tinggui. Experimental Study of the Volume Drying Shrinkage Characteristics of Lignite under Low Temperatures // ACS Omega. 2022. Vol. 7. Iss. 12. P. 10029-10038. DOI: 10.1021/acsomega.1c05575
- Rongtang Liu, Ming Liu, Xiaoqu Han, Junjie Yan. Drying characteristics and kinetics analyses for Yimin lignite at various temperatures // Drying Technology. 2021. Vol. 39. Iss. 7. P. 912-924. DOI: 10.1080/07373937.2020.1729174
- Fu B.A., Chen M.Q. Thin-layer drying kinetics of lignite during hot air forced convection // Chemical Engineering Research and Design. 2015. Vol. 102. P. 416-428. DOI: 10.1016/j.cherd.2015.07.019
- Haijun Zhou, Yuanquan Xiong, Yu Pei. Effect of moisture content on dense-phase pneumatic conveying of pulverized lignite under high pressure // Powder Technology. 2016. Vol. 287. P. 355-363. DOI: 10.1016/j.powtec.2015.10.026
- Celen P., Erdem H.H. An experimental investigation of single lignite particle dried in superheated steam and hot air // International Journal of Coal Preparation and Utilization. 2018. Vol. 41. Iss. 12. P. 845-854. DOI: 10.1080/19392699.2018.1536047
- Fu B.A., Chen M.Q., Huang Y.W. Heat transfer characteristics on lignite thin-layer during hot air forced convective drying // Fuel. 2015. Vol. 154. P. 132-139. DOI: 10.1016/j.fuel.2015.03.075
- Hosseini T., Zhang L. Process modeling and techno-economic analysis of a solar thermal aided low-rank coal drying-pyrolysis process // Fuel Processing Technology. 2021. Vol. 220. № 106896. DOI: 10.1016/j.fuproc.2021.106896
- Цзиньчжань Хуан, Чжицян Ли, Бяо Чэнь и др. Оперативный контроль элементного состава угольной золы на основе машинного обучения и рентгеновской флуоресценции // Записки Горного института. 2022. Т. 256. С. 663-676. DOI: 10.31897/PMI.2022.89
- Bojian Qi, Yong Yan, Wenbiao Zhang, Xueyao Wang. Measurement of biomass moisture content distribution in a fluidised bed dryer through electrostatic sensing and digital imaging // Powder Technology. 2021. Vol. 388. P. 380-392. DOI: 10.1016/j.powtec.2021.04.096
- Ji Hyeon Park, Jung Hae Park, Soo Chul Kim. A Study on Application of Enzyme Additives to Improve Drying Speed of Urushi Lacquer // Journal of the Korean Wood Science and Technology. 2020. Vol. 48. № 3. P. 326-344. DOI: 10.5658/WOOD.2020.48.3.326
- Huaigang Cheng, Lixiang Wu, Fangqin Cheng. Kinetics of static immersed leaching of low-grade sea-type evaporites based on theoretical and experimental investigation of unsteady-state mass transfer // Journal of Cleaner Production. 2020. Vol. 256. № 120501. DOI: 10.1016/j.jclepro.2020.120501
- Yuwei Wei, Xishan Zhu, Chenquan Deng et al. Study on cracking process of hot pressed tee based on Fick’s second law // Engineering Failure Analysis. 2022. Vol. 134. № 106014. DOI: 10.1016/j.engfailanal.2021.106014
- Lingbo Kong, Xing Yang, Zhihao Hou, Jixian Dong. Mathematical Modeling of Drying Kinetics for Pulp Sheet Based on Fick’s Second Law of Diffusion // Journal of Korea TAPPI. 2020. Vol. 52. № 2. P. 23-31. DOI: 10.7584/JKTAPPI.2020.04.52.2.23
- Cheak Theng Ee, Ching Lik Hii, Sze Pheng Ong et al. Convective Air Drying of Spondias Dulcis and Product Quality // International Journal of Food Engineering. 2019. Vol. 15. Iss. 3-4. № 20180228. DOI: 10.1515/ijfe-2018-0228
- Obradović B. Guidelines for general adsorption kinetics modeling // Hemijska industrija. 2020. Vol. 74. Iss. 1. P. 65-70. DOI: 10.2298/HEMIND200201006O
- Yousuf M. A second-order efficient L-stable numerical method for space fractional reaction–diffusion equations // International Journal of Computer Mathematics. 2018. Vol. 95. Iss. 6-7. P. 1408-1422. DOI: 10.1080/00207160.2018.1435865
- Pengbo Fu, Hao Yu, Qiqi Li et al. Cyclone rotational drying of lignite based on particle high-speed self-rotation: Lower carrier gas temperature and shorter residence time // Energy. 2022. Vol. 244. Part B. № 123005. DOI: 10.1016/j.energy.2021.123005
- Ying Xu, Jiming Wang, Guojie Zhang et al. Evaluation of hydrothermal treatment on physicochemical properties and re-adsorption behaviors of lignite // Energy. 2022. Vol. 244. Part A. № 122597. DOI: 10.1016/j.energy.2021.122597
- Crapse J., Pappireddi N., Gupta M. et al. Evaluating the Arrhenius equation for developmental processes // Molecular Systems Biology. 2021. Vol. 17. Iss. 8. № e9895. DOI: 10.15252/msb.20209895
- Jaeho Cha, Sungho Yoon. Determination of shift factor for long-term life prediction of carbon/fiber epoxy composites using the time-temperature superposition principle // Functional Composites and Structures. 2022. Vol. 4. Iss. 1. № 015003. DOI: 10.1088/2631-6331/ac529e
- Selimefendigil F., Coban S.O., Öztop H.F. An efficient method for optimizing the unsteady heat and mass transport features for convective drying of two porous moist objects in a channel // International Journal of Mechanical Sciences. 2021. Vol. 200. № 10644. DOI: 10.1016/j.ijmecsci.2021.106444
- Joardder M.U.H., Karim M.A. Development of a porosity prediction model based on shrinkage velocity and glass transition temperature // Drying Technology. 2019. Vol. 37. Iss. 15. P. 1988-2004. DOI: 10.1080/07373937.2018.1555540
- Ternes S., Börnhorst T., Schwenzer J.A. et al. Drying Dynamics of Solution-Processed Perovskite Thin-Film Photovoltaics: In Situ Characterization, Modeling, and Process Control // Advanced Energy Materials. 2019. Vol. 9. Iss. 39. № 1901581. DOI: 10.1002/aenm.201901581
- Chicco D., Tötsch N., Jurman G. The Matthews correlation coefficient (MCC) is more reliable than balanced accuracy, bookmaker informedness, and markedness in two-class confusion matrix evaluation // BioData Mining. 2021. Vol. 14. № 13. DOI: 10.1186/s13040-021-00244-z
- Jia-Qing Zhou, Hong-Bin Liu, Changdong Li. A semi-empirical model for water inflow into a tunnel in fractured-rock aquifers considering non-Darcian flow // Journal of Hydrology. 2021. Vol. 597. № 126149. DOI: 10.1016/j.jhydrol.2021.126149
- Xun Zhang, Bin Zeng, Bing Lu et al. Experimental research on spontaneous combustion of coal oxidized by ultraviolet photocatalysis // AIP Advances. 2022. Vol. 12. Iss. 8. № 085226. DOI: 10.1063/5.0098407
- Pengfei Zhao, Liping Zhong, Yuemin Zhao, Zhenfu Luo. Comparative studies on the effect of mineral matter on physico-chemical properties, inherent moisture and drying kinetics of Chinese lignite // Energy Conversion and Management. 2015. Vol. 93. P. 197-204. DOI: 10.1016/j.enconman.2015.01.020
- Jung J., Kobayashi C., Sugita Y. Optimal Temperature Evaluation in Molecular Dynamics Simulations with a Large Time Step // Journal of Chemical Theory and Computation. 2019. Vol. 15. Iss. 1. P. 84-94. DOI: 10.1021/acs.jctc.8b00874
- Meng Liu, Jian Li, Yufeng Duan. Effects of solvent thermal treatment on the functional groups transformation and pyrolysis kinetics of Indonesian lignite // Energy Conversion and Management. 2015. Vol. 103. P. 66-72. DOI: 10.1016/j.enconman.2015.06.047
- Liu Ming Qiang, Jian Zhong Liu, Yu Jie Yu et al. Investigation of Lignite Combustion Characteristics with Thermal Analysis // Advanced Materials Research. 2012. Vol. 614-615. P. 25-30. DOI: 10.4028/www.scientific.net/AMR.614-615.25
- Yanyan Shi, Shuyuan Li, Haoquan Hu. Studies on pyrolysis characteristic of lignite and properties of its pyrolysates // Journal of Analytical and Applied Pyrolysis. 2012. Vol. 95. P. 75-78. DOI: 10.1016/j.jaap.2012.01.008
- Lei Guo, Chenhui Liu, Srinivasakannan C., Gao Jiyun. Microwave upgradation of Yunnan lignite: dielectric properties, drying pattern and kinetics // Journal of Microwave Power and Electromagnetic Energy. 2021. Vol. 55. Iss. 3. P. 248-269. DOI: 10.1080/08327823.2021.1952834
