Сопоставление подходов к оценке сжимаемости порового пространства
- 1 — д-р техн. наук главный научный сотрудник Институт физики Земли РАН ▪ Orcid ▪ Elibrary
- 2 — д-р физ.-мат. наук заместитель директора Институт физики Земли РАН ▪ Orcid
Аннотация
Рассматриваются интегральный и дифференциальный подходы к определению объемного сжатия горных пород, вызванного изменениями напряженного состояния. Анализируются изменения объема порового пространства горных пород при увеличении его всестороннего обжатия. Оценка изменений коэффициентов сжимаемости коллекторов, обусловленных разработкой месторождений, является актуальной проблемой, поскольку разброс величин коэффициентов сжимаемости снижает адекватность оценок изменений физических свойств и просадок земной поверхности разрабатываемых месторождений и подземных хранилищ газа. Этот параметр является ключевым при оценке геодинамических последствий длительной разработки месторождений углеводородов и эксплуатации подземных хранилищ газа. Подходы к оценке отличаются применением накопленных (интегральных) или локальных (дифференциальных) изменений пористости при перемене эффективного давления. Показано, что коэффициент объемной сжимаемости пор, рассчитанного по интегральному подходу, значительно превышает его величину, рассчитанную по дифференциальному подходу, что обусловлено накопительным характером сжатия пор при росте эффективного давления. Показано, что дифференциальный подход точнее определяет величину коэффициента сжимаемости пор, так как детальнее учитывает особенности изменения эффективного давления.
Введение
Физические свойства горных пород-коллекторов делятся на две основные категории: фильтрационно-емкостные и деформационно-прочностные. При этом свойства пород первой категории, в первую очередь пористость и проницаемость, являются базовыми при составлении проектов разработки месторождений углеводородов и подсчете их запасов [1-3]. Деформационно-прочностные характеристики горных пород [4-6] (коэффициент сжимаемости порового объема и предел прочности) эффективно используются, в основном, для оценки деформационных последствий длительной разработки нефтегазовых месторождений и подземных хранилищ газа [7-9]. Изменения напряженно-деформированного состояния вызывают реакцию горных пород, которая характеризуется коэффициентом объемной сжимаемости [10, 11]. Наиболее известны техногенные изменения напряженно-деформированного состояния недр, обусловленные разработкой месторождений нефти и газа, которые сопровождаются изменениями физических свойств горных пород-коллекторов [8, 12]. Определение объемной сжимаемости насыщенных флюидами пород очень важно для разработки месторождений углеводородов [10, 13]. Ее роль состоит в том, что нефть и газ могут быть выдавлены в скважины под действием давления вышележащих пород при разработке месторождений на истощение [14, 15]. Также нефть может быть вытеснена в добывающие скважины специальными жидкостями, закачиваемыми в пласт. В этом случае на добычу кроме других факторов будет влиять фактическая объемная сжимаемость пор. Точное определение коэффициента объемной сжимаемости порового пространства особенно важно в пластах слабо консолидированных пород, где большая величина сжимаемости пор может привести к значительным просадкам земной поверхности [16, 17].
Существует много способов определения сжимаемости горных пород [18, 19], но только в редких случаях указывается, в каких условиях и при каких давлениях они были получены [6, 20]. Большие расхождения величины коэффициентов сжимаемости значительно влияют на адекватность оценок изменений физических свойств [21, 22] и просадок земной поверхности разрабатываемых месторождений углеводородов и подземных хранилищ газа [23, 24].
Зависимость коэффициента сжимаемости порового объема от величины эффективного давления носит ярко выраженный нелинейный характер [25, 26]. Поэтому важно знать, в каком диапазоне изменений эффективного давления производилась оценка коэффициента поровой сжимаемости [27, 28]. Это побудило авторов рассмотреть более детально имеющиеся походы к оценке сжимаемости и выбрать из них наиболее точные и адекватно отображающие изменения напряженного состояния горных пород, не превышающие их предел упругости и/или прочности.
Целью работы является анализ и сопоставление имеющихся подходов к оценке сжимаемости горных пород и выбор из них наиболее адекватно отражающего изменения в пласте эффективного давления в процессе разработки месторождений нефти и газа и эксплуатации подземных хранилищ газа.
Методология
В сжимаемых пористых породах изменения либо объема пор Vp, либо объема образца горной породы Vb вызываются изменениями порового давления или всестороннего давления [28-30]. Сжимаемость объема пор зависит от изменений давления всестороннего сжатия
либо изменений порового давления
на практике зачастую применяется величина эффективного давления
где Рс – давление всестороннего сжатия; Рр – давление порового (пластового) флюида (вода, нефть, газ); α – коэффициент Био, иногда называющийся коэффициентом разгрузки, характеризует ту часть порового давления, которая противодействует всестороннему давлению.
Коэффициент α принимается равным единице в случае проницаемых горных пород с пористостью более 3-5 % [31, 32]. Тогда Cpc и Cpp будут равны, так как равные по величине изменения всестороннего и порового давления вызывают одинаковые изменения объема порового пространства, но знаки их будут противоположны. При этом уменьшение объема порового пространства будет вызываться либо ростом всестороннего сжатия, либо снижением порового давления [33].
В нашем случае эксперименты проводились в условиях, когда Pp = const, а изменение Peff достигалось ростом всестороннего сжатия. В этом случае уместно обозначение Cpc = Cp. Коэффициент поровой сжимаемости экспоненциально зависит от эффективного давления, что можно обосновать, используя представления линейной пороупругости.
Как известно, коэффициент сжимаемости порового пространства определялся по формуле
где ΔVp – изменение объема порового пространства (объем поровой жидкости, выдавливаемой из образца), см3; Vp0 – начальный объем порового пространства образца, см3; ΔPeff – изменения эффективного давления, МПа.
Многочисленные эксперименты свидетельствуют о том, что с увеличением эффективного давления коэффициент поровой сжимаемости уменьшается. В дифференциальной форме это соответствует уравнению
где b – эмпирический коэффициент, который различается для разных горных пород и характеризует интенсивность изменения сжимаемости с изменением эффективного давления, МПа–1.
При интегрировании уравнения (5) в диапазоне изменений коэффициента сжимаемости от начального значения Ср0 до конечного Cp и от начального эффективного давления Peff 0 до конечного Peff получается равенство
При интегрировании и подставлении пределов получается экспоненциальная зависимость Ср от ΔPeff :
или
Типичная зависимость коэффициента объемной сжимаемости порового пространства от изменения эффективного давления (рис.1): увеличение эффективного давления от 0,1 до 37,0 МПа; уравнение аппроксимации тренда Ср = 0,0062е–0,0259Pеff; коэффициент детерминации R2 = 0,98; интенсивность изменения сжимаемости с изменением эффективного давления b = –0. Естественно, что при такой зависимости коэффициента сжимаемости от эффективного давления оценка коэффициента будет различаться для разных диапазонов изменения давления.
В данном случае использовались 34 песчано-глинистых образца вендского возраста Чаяндинского месторождения в условиях, моделирующих пластовые: пористость в атмосферных условиях составляет 3-15,6 %, проницаемость по газу от 2·10–15 до 100·10–15 м2, глубина, с которой был поднят керн 1660-1860 м. Образцы представлены в основном крупно- и мелкозернистыми песчаниками кварцевого и кварц-полевошпатового состава со смешанным кварц-регенерационным, сульфатным, глинисто-пленочным и частично базальным цементом [34].
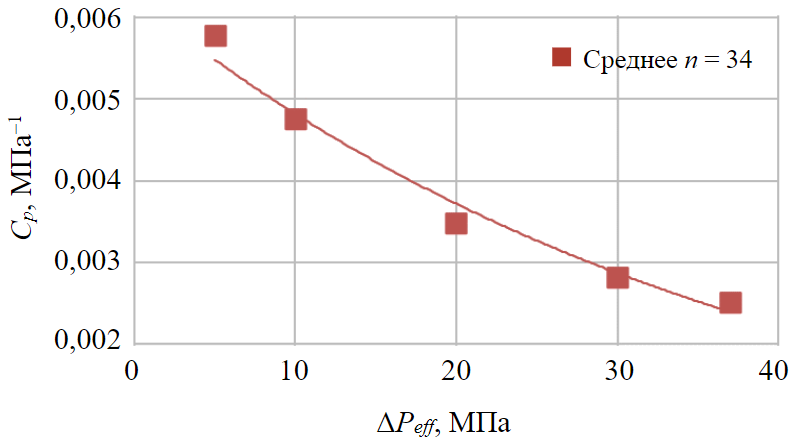
Рис.1. Изменение среднего значения объемной сжимаемости порового пространства по 34 образцам, которое определено по накапливаемому объему жидкости, выжатой из образцов (интегральный подход)
В зависимости от выбранного интервала изменения эффективного давления возможны два подхода к оценке коэффициента поровой сжимаемости – интегральный и дифференциальный. Это особенно актуально, когда значения коэффициентов поровой сжимаемости используются для оценки аномальных деформаций земной поверхности различных нефтегазовых объектов. Так, например, при оценке оседаний земной поверхности при эксплуатации нефтяных месторождений необходимо учитывать закачку жидкости при проведении процедуры поддержания пластового давления (ППД), которая может восстанавливать начальное пластовое давление и, соответственно, эффективное давление до начальной величины после произведенного отбора жидкости из пласта и снижения пластового давления, что может привести к уменьшению просадок, вплоть до нулевых значений. При закачке в пласт возможны и более сложные эффекты, которые выходят за рамки пороупругих представлений, на которых базируется данная работа. При разработке газовых месторождений в режиме истощения увеличение эффективного давления происходит монотонно за длительный промежуток времени. Эксплуатация подземных хранилищ газа (ПХГ) происходит циклическим образом, что приводит к необходимости учета интервалов знакопеременного изменения
эффективного давления. Различные режимы изменения эффективного давления при эксплуатации нефтегазовых объектов приводят к необходимости использования различных подходов к определению значений коэффициента поровой сжимаемости.
Интегральный (осредненный) подход подразумевает оценку коэффициента сжимаемости за весь интервал изменения эффективного давления. В частности, изменение коэффициента ΔCp определяется суммарно за весь интервал изменения эффективного давления от Peff 0 до Peff. Обычно в качестве начального принимается величина коэффициента сжимаемости при эффективном давлении, близком к атмосферному (0,1-2,0 МПа), а за конечное – величина коэффициента сжимаемости при эффективном давлении для условий, моделирующих пластовые [31, 35], например, 37,0 МПа.
Дифференциальный подход предполагает оценку изменения значений коэффициентов сжимаемости в выбранном интервале изменения эффективного давления. Следует отметить, что дифференциальный подход имеет две формы представления: накопительную и дискретную. В первом варианте изменение порового объема отсчитывается от начальной величины Vp0, и измеряется его уменьшение за интервалы изменения ΔPeff, которые последовательно увеличиваются в диапазонах, например, 0,1-5,0; 0,1-10,0; 0,1-20,0 и т.д. до интервала 0,1-37 МПа. Во втором варианте изменение порового объема каждый раз отсчитывается от величины Vp, которая соответствует тому значению эффективного давления, с которого начинается интервал его изменения, например, 0,1-5,0; 5,0-10,0; 10,0-20,0; 20,0-30,0 и 30,0-37,0 МПа.
Методика и объект исследований
Методика экспериментальных исследований, подробно описанная в работе [33], позволяет напрямую измерить объем поровой жидкости ΔVp, выжатой из образца, и рассчитать не только изменения пористости, но и объемную деформацию образца. Исследовались образцы песчаника цилиндрической формы диаметром 30 мм и длиной 30 мм, которые подвергались всестороннему сжатию при управляемом давлении поровой жидкости. Использование методики, позволяющей измерить объем поровой жидкости, выдавливаемой из образца при увеличении всестороннего обжатия образца, дало возможность определить изменения порового объема [34]. Величина ΔVp в пластовых условиях определена с учетом того, что коэффициент сжимаемости твердой матрицы горной породы на несколько порядков превосходит коэффициент сжимаемости порового пространства.
При проведении петрофизических исследований по данной методике давление и температуру поровой жидкости (модель пластовой воды) поддерживали постоянными (13 МПа, 20 °С), только увеличивая всестороннее давление до 37 МПа. Поэтому учет коэффициента сжимаемости жидкости от давления и температуры не требовался. Таким образом, исходя из формулы (4), определялся коэффициент объемной сжимаемости порового пространства при изменении эффективного давления.
В этом случае для оценки коэффициента сжимаемости можно предложить подход на основе исключительно измеряемых в ходе эксперимента параметров: объема порового пространства ΔVp и вариаций эффективного давления ΔPeff. Для этого формулу (4) можно преобразовать в дифференциальном виде:
Из уравнения (9) следует дифференциальное уравнение
Тогда, проводя интегрирование уравнения (10) в диапазоне изменений порового объема от начального значения Vp0 до конечного Vp и от начального эффективного давления Peff 0 до конечного Peff , получается
или
При сравнении формул (7), (8) и (11), (12) видно, что формулы (11), (12) для определения коэффициента сжимаемости содержат только измеряемые в данном эксперименте величины, а в формулы (7), (8) входит коэффициент b, который необходимо определять из дополнительных экспериментов.
Обсуждение
Интегральный подход
Определение коэффициента сжимаемости объема пор в соответствии с интегральным подходом можно выполнить графическим способом (рис.2), используя линейную зависимость изменений логарифма объема пор от эффективного давления. Из формулы (11) следует
Если построить полулогарифмический график зависимости ln(Vp) от эффективного давления, то получается уравнение наклонной прямой с постоянным угловым коэффициентом, равным Ср (рис.2). Наклон графика – среднее значение коэффициента объемной сжимаемости порового пространства в соответствии с интегральным подходом. Значение ln(Vp0) определяется из условия ΔPeff = 0. При этом величина ln(Vр) является безразмерной, которая показывает степень, в которую (~2,72) должно быть возведено число, равное текущему объему пор (Vр).
Полученная экспериментальная зависимость может быть с высокой достоверностью (R2 = 0,94) описана логарифмическим уравнением (11):
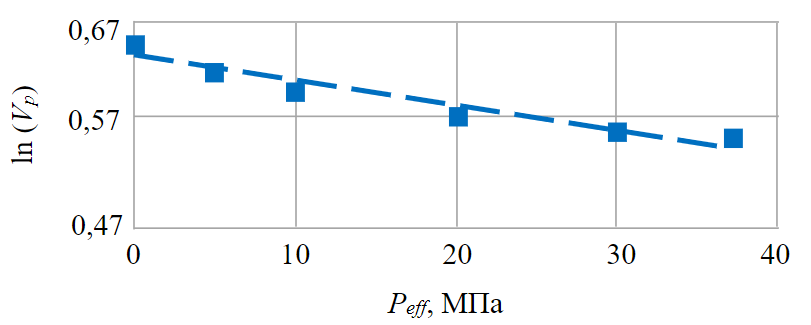
Рис.2. Изменение объема пор при увеличении эффективного давления в полулогарифмическом масштабе

Рис.3. Графическое определение коэффициента объемной сжимаемости порового пространства с применением дифференциально-накопительного подхода при росте эффективного давления 1 – 0,1-5; 2 – 0,1-10; 3 – 0,1-20; 4 – 0,1-30; 5 – 0,1-37 МПа
При этом средняя величина коэффициента составляет –0,00249 МПа–1 (наклон графика на рис.2) на интервале изменений эффективного давления 0,1-37,0 МПа. А свободный член уравнения (14) 0,631 соответствует натуральному логарифму объема пор в начальном состоянии.
Таким образом, интегральный подход может быть применен для графической оценки средней величины коэффициента объемной сжимаемости пор при разработке месторождений углеводородов только по данным об изменении объема порового пространства от начального значения Vp0 до текущего Vp при изменении эффективного давления от начального до соответствующего пластовым условиям. Однако, нелинейный характер изменения коэффициента сжимаемости от эффективного давления (см. рис.1) вызывает необходимость подробного исследования этой зависимости для различных интервалов изменения давления.
Дифференциальный подход
На основе имеющихся экспериментальных данных весь интервал изменений эффективного давления 0,1-37,0 МПа был разбит на локальные отрезки: 0,1-5,0; 0,1-10,0; 0,1-20,0; 0,1-30,0 и 0,1-37,0 МПа. При этом за начальные приняты величины порового объема при эффективном давления 0,1 МПа; за конечные приняты величины 5,0; 10,0; 20,0; 30,0; 37,0 МПа. На рис.3 показаны изменения деформации пор при дифференциально-накопительном подходе с ростом эффективного давления.
Изменения деформации пор равны нулю при Рeff = 0,1 МПа и увеличиваются по мере роста эффективного давления, аппроксимированы линейными зависимостями, наклон которых и является коэффициентом объемной сжимаемости пор Срi (4). Величина Ср равна: –0,005653; –0,004895; –0,003795; –0,003175 и –0,002845 МПа–1 при изменениях Реff : 0,1-5,0; 0,1-10,0; 0,1-20,0; 0,1-30,0 и 0,1-37,0 МПа соответственно.
Различным интервалам изменения эффективного давления соответствуют разные значения коэффициента поровой сжимаемости (рис.3). Это необходимо учитывать при оценке итоговых оседаний газовых месторождений, разрабатываемых в режиме истощения [13, 14, 34].

Рис.4. Графическое определение коэффициента объемной сжимаемости порового пространства с применением дифференциально-дискретного подхода по каждому интервалу изменения эффективного давления и изменению при этом объемной деформации пор 1 – 0,1-5; 2 – 5-10; 3 – 10-20; 4 – 20-30; 5 – 30-37 МПа
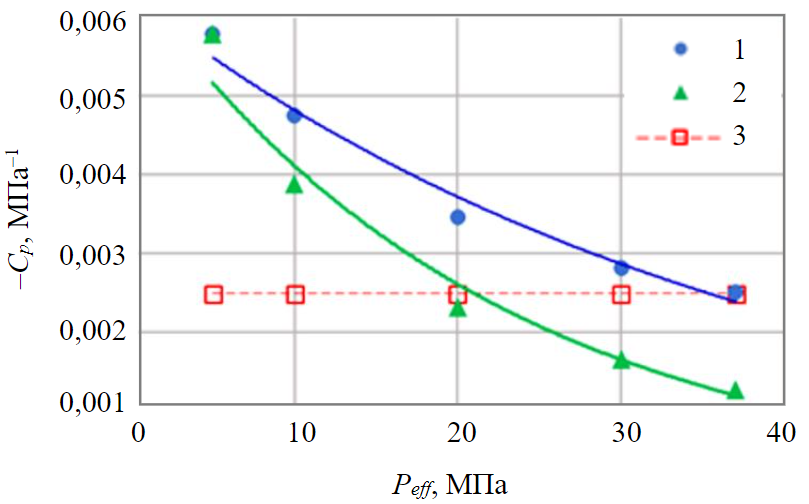
Рис.5. Изменение коэффициента сжимаемости объема пор по 34 образцам, определенных при увеличении эффективного давления от 0,1 до 37 МПа 1 – дифференциально-накопительный подход уравнение аппроксимации dVpi/Vp0 (см. рис.3); 2 – дифференциально-дискретный dVp(i+1)/Vpi n = 34 (см. рис.4); 3 – интегральный, среднее по (13) n = 34; Ср = –0,00249 МПа–1(см. рис.2)
Использование дифференциально-дискретного подхода приведено на рис.4, где представлены линейные зависимости изменений объемной деформации пор от изменений эффективного давления. В отличие от дифференциально-накопительного подхода, начальными служат значения порового объема в начале каждого отдельного интервала: 0,1; 5; 10; 25; 30; 37 МПа. Изменения деформации пор равны нулю при Рeff , равном 0,1; 5; 10; 20 и 30 МПа, и увеличиваются по мере роста эффективного давления и аппроксимированы линейными зависимостями, наклон которых и является коэффициентом объемной сжимаемости пор Срi (4).Получены значения Ср: –0,005771; –0,003880; –0,002319; –0,001669, –0,001284 МПа–1 при следующих изменениях Реff : 0,1-5,0; 5,0-10,0; 10,0-20,0; 20,0-30,0 и 30,0-37,0 МПа соответственно.
Коэффициент объемной сжимаемости пор в этом случае определяется по наклону прямых, соединяющих начальное и конечное значения объемной деформации пор при увеличении эффективного давления. В отличие от дифференциально-накопительного подхода, для нормирования (отношения изменений порового объема к первоначальному значению) изменений объемной деформации пор ΔVp/Vp используются величины объема пор при начальном значении эффективного давления каждой ступени его роста. На рис.4 более наглядно проявились как общее уменьшение значения коэффициента объемной сжимаемости (от –0,00577 до –0,00128 МПа–1), так и немонотонный характер уменьшения с ростом эффективного давления.
Дифференциально-дискретный подход может быть применен при различных изменениях эффективного давления как при увеличении, так и при уменьшении. Однако необходимо обладать информацией об объеме пор и их изменении на каждом этапе процесса разработки. Особенно актуально это при оценке аномальных деформаций земной поверхности во время эксплуатации подземных хранилищ газа, где реализуется знакопеременное изменение пластового давления.
Сопоставление оценок коэффициента объемной сжимаемости пор
Сравнение значений коэффициентов сжимаемости объема пор, которые получены экспериментально по объемам жидкости, выжатой из образцов на каждом этапе роста эффективного давления, и рассчитаны по интегральному и дифференциальному подходам, показаны на рис.5.
Анализируя приведенные рис.1-5, можно увидеть, что величина коэффициента объемной сжимаемости, максимальная при начальных (минимальных) значениях эффективного давления, уменьшается с его ростом и может быть с высокой степенью достоверности (R2 = 0,98) аппроксимирована экспоненциальной зависимостью (8) (см. рис.1). При этом могут быть использованы как интегральный, так и дифференциальный подходы. А среднее значение при изменении Peff от 0,1 до 37,0 МПа при интегральном подходе может быть оценено еще по формуле (13) (см. рис.2, 5).
Величины коэффициента объемной сжимаемости пор сведены в таблицу.
Сопоставление коэффициентов сжимаемости пор (Ср, 103·МПа–1), рассчитанных при различных подходах
|
Подход |
Рeff, МПа |
|||||
|
0,1 |
5,0 |
10,0 |
20,0 |
30,0 |
37,0 |
|
|
Интегральный по изменениям объема пор ln (Vp) |
– |
–2,495 |
–2,495 |
–2,495 |
–2,495 |
–2,495 |
|
Дифференциально-накопительный по накопленной объемной деформации пор dVрi/Vр0 |
– |
–5,771 |
–4,753 |
–3,469 |
–2,823 |
–2,508 |
|
Дифференциально-дискретный по ступеням изменения Рeff и объемной деформации пор dVрi+1/Vрi |
– |
–5,771 |
–3,880 |
–2,319 |
–1,669 |
–1,284 |
При начальном эффективном давлении (5,0 МПа) интегральный подход существенно занижает коэффициент сжимаемости пор. Дифференциально-накопительный и дифференциально-дискретный подходы при этом совпадают. Очевидно, что интегральный и дифференциально-накопительный подходы существенно завышают (до 95,4 %) величину коэффициента сжимаемости пор при эффективных давлениях, близких к пластовым (30-37 МПа) (рис.5). Также очевидно, что применение дифференциально-дискретного подхода дает значения коэффициента сжимаемости пор, более адекватно отвечающие напряженному состоянию пласта.
Известно, что эффективные давления в разрабатываемом пласте могут изменяться в диапазоне ±10-20 МПа [8, 36]. При этом предлагаемый авторами дифференциальный (дифференциально-дискретный) подход позволяет оценить величину сжимаемости порового пространства даже при отсутствии лабораторных исследований сжимаемости керна. Легко показать, что изменение нормированной пористости равно нормированному изменению порового объема: Δm/m0 = ΔVp/Vp0. Тогда, используя значения изменений коэффициента пористости, получаемых при каротаже скважин в рамках ГИС-контроля процесса разработки месторождения или эксплуатации ПХГ, можно оценить коэффициент сжимаемости объема пор при известных изменениях эффективного давления. Дифференциальный подход позволяет более верно оценивать величины возможных просадок земной поверхности на различных стадиях разработки месторождений.
Аналогично во время эксплуатации ПХГ для оценки коэффициента сжимаемости пор рекомендуется использование дифференциально-дискретного подхода с целью более правильного (дифференцированного) учета изменений эффективного давления, происходящих в пласте в периоды закачки-отбора газа. Принципиально важно, что значения коэффициентов сжимаемости объема пор будут различны для периода закачки и отбора газа даже при одинаковом изменении пластового (эффективного) давления. Это происходит потому, что одинаковые (с учетом знака) изменения порового объема нормируются (делятся) на разные значения порового объема, соответствующие различным значениям эффективного давления. Например, при увеличении эффективного давления от 10 до 20 МПа величина изменения порового объема ΔVp0 делится на значение порового объема Vp0, которое соответствует значению 10 МПа. При снижении эффективного давления от 20 до 10 МПа идентичное предыдущему изменение порового объема ΔVp (в данном случае увеличение) нормируется на значение Vp0, которое соответствует значению эффективного давления 20 МПа. Естественно, во втором случае коэффициент сжимаемости будет больше, чем в первом, поскольку знаменатель дроби ΔVp/Vp0 в первом случае будет больше, чем во втором. Это необходимо учитывать при детальном анализе результатов геодинамического мониторинга подземных хранилищ газа.
Результаты обсуждения экспериментальных данных позволяют рекомендовать лабораторные дифференциальные подходы (накопительный и дискретный) для практического определения коэффициента объемной сжимаемости пор, поскольку исключаются прочие внешние факторы и неопределенности в величинах давлений, которые присутствуют в промысловых определениях при разработке месторождений. Метод ГИС-контроля с использованием изменений пористости можно рекомендовать как уточняющий метод, направленный на мониторинг изменений объемной сжимаемости порового пространства и подтверждения лабораторных результатов. Для детального анализа изменений напряженного состояния объектов подземного хранения газа можно рекомендовать дифференциально-дискретный подход к оценке коэффициента объемной сжимаемости пор, в качестве позволяющего учитывать знакопеременные изменения пластового давления.
Последовательный учет различий коэффициентов сжимаемости позволяет также изучать такой важный эмпирический факт как слабое оседание земной поверхности длительно разрабатываемых газовых месторождений в режиме истощения, который был отмечен по результатам длительного мониторинга на месторождении в Туркменистане [8, 37]. Для его объяснения была использована генетическая модель формирования оседаний территории месторождений, в которой использовалась связь относительных изменений коэффициента поровой сжимаемости и относительных изменений объемного модуля K вмещающей среды в обстановке постоянно действующих (квазистатических) напряжений, сформировавших структуру антиклинального поднятия, за геологическое время, к которому приурочено месторождение. Эти силы (напряжения) способствуют поднятию земной поверхности, компенсирующему оседание, в условиях падения эффективной жесткости (объемного модуля) резервуара. Из геомеханики известно, что коэффициент сжимаемости обратно пропорционален K [6, 8]. Относительные (нормированные) изменения коэффициента сжимаемости Ср связаны с относительными изменениями объемного модуля следующей формулой:
Знак минуса в уравнении (15) означает, что при увеличении коэффициента сжимаемости значение объемного модуля снижается, и наоборот. Соотношение (15) позволяет производить переход от петрофизических моделей к моделям пороупругой неоднородности, на основе которой можно оценивать изменение напряженно-деформированного состояние разрабатываемого пласта (пластов) нефтегазовых месторождений и подземных хранилищ газа.
Научная новизна работы заключается в аналитическом обосновании экспоненциальной зависимости коэффициента сжимаемости пор от эффективного давления, которое было ранее предположено в работе [34] и подтверждено результатами экспериментальных исследований на образцах горных пород.
Заключение
Сопоставление интегрального и дифференциального подходов к определению коэффициента объемной сжимаемости порового пространства образцов горных пород подчеркивает затухающий характер его снижения с ростом эффективного давления, которое с высокой степенью достоверности можно аппроксимировать экспоненциальной зависимостью, что доказано в рамках использования базовых соотношений геомеханики пороупругих сред. Выявлено, что коэффициент объемной сжимаемости пор, рассчитанный по интегральному подходу существенно больше (до 130 %) коэффициента, рассчитанного с помощью дифференциального подхода. Это различие обусловлено накопительным характером уменьшения объема пор с увеличением эффективного давления. Очевидно, что, дифференциальный подход позволяет точнее определить величину сжимаемости порового пространства за счет более соответствующего учета изменений, действующего в пласте эффективного давления и может быть рекомендован для оценки динамики физических свойств горных пород в процессе разработки месторождений нефти и газа и эксплуатации ПХГ, а также для изучения аномальных деформаций земной поверхности в пределах этих объектов.
Литература
- Блинова Е.Ю., Индрупский И.М., Закиров Э.С., Коваленко К.В. Учет неоднородности сжимаемости коллектора при построении гидродинамических моделей продуктивных пластов // Геология, геофизика и разработка нефтяных и газовых месторождений. 2012. № 12. С. 32-35.
- Габсия Б.К. Особенности определения коэффициентов вытеснения при моделировании разработки низкопроницаемых и сложнопостроенных пластов-коллекторов нефтяных и газовых месторождений // Нефтяное хозяйство. 2017. № 7. С. 50-53. DOI: 10.24887/0028-2448-2017-7-50-53
- Галкин С.В., Кривощеков С.Н., Козырев Н.Д. и др. Учет геомеханических свойств пласта при разработке многопластовых нефтяных месторождений // Записки Горного института. 2020. Т. 244. С. 408-417. DOI: 10.31897/PMI.2020.4.3
- Кашников Ю.А., Шустов Д.В., Кухтинский А.Э., Кондратьев С.А. Геомеханические характеристики терригенных продуктивных объектов нефтяных месторождений Западного Урала // Нефтяное хозяйство. 2017. № 4. С. 32-35. DOI: 10.24887/0028-2448-2017-4-32-35
- Кашников Ю.А. Ашихмин С.Г. Механика горных пород при разработке месторождений углеводородного сырья. М.: Изд-во «Горная книга», 2019. 552 с.
- Fjær E. Relations between static and dynamic moduli of sedimentary rocks // Geophysical Prospecting. Vol. 67. Iss. 1. P. 128-139. DOI: 10.1111/1365-2478.12711
- Кашников Ю.А., Ашихмин С.Г., Шустов Д.В. и др. Повышение эффективности разработки месторождений углеводородов на основе комплексных геомеханических исследований // Нефтяное хозяйство. 2019. № 3. С. 66-69. DOI: 10.24887/0028-2448-2019-3-66-69
- Кузьмин Ю.О. Деформационные последствия разработки месторождений нефти и газа // Геофизические процессы и биосфера. 2021. Т. 20. № 4. С. 103-121. DOI: 10.21455/GPB4-7
- Кузьмин Ю.О. Современные объемные деформации разломных зон // Физика Земли. № 4. С. 3-18. DOI: 10.31857/S0002333722040068
- Sharifi J., Saberi M.R. Quantitative Evolution Fracture Porosity a Carbonate Reservoir Using Analytical Method // 83rd EAGE Annual Conference, 6-9 June 2022. DOI: 10.3997/2214-4609.202210135
- Zhukov V.S., Kuzmin D.K., Kuzmin Yu.O., Pleshkov I.V. Comparison of forecast estimates of seabed subsidence of the Yuzhno-Kirinskoye field // IV National Scientific Conference with Foreign Participants: Geodynamical Processes and Natural Hazards (4th GeoProNH 2021), 6-10 September 2021, Yuzhno-Sakhalinsk, Russian Federation. IOP Conference Series: Earth and Environmental Science. 2021. Vol. 946. № 012019. DOI: 10.1088/1755-1315/946/1/012019
- Жуков В.С., Семенов Е.О., Кузьмин Ю.О. Динамика физических свойств коллекторов при разработке месторождений нефти и газа // Вести газовой науки. 2018. № 5 (37). С. 82-99.
- Жуков В.С., Иванов П.Ю. Изменение физических свойств коллектора как результат роста эффективного давления в процессе разработки месторождения (моделирование на примере Южно-Киринского месторождения) // Вести газовой науки. 2015. № 4 (24). С. 144-148.
- Sharifi J., Saberi M.R., Javaherian A., Moghaddas N.Н. Investigation of static and dynamic bulk moduli in a carbonate field // Exploration Geophysics. 2021. Vol. 52. Iss. 1. P. 16-41. DOI: 10.1080/08123985.2020.1756693
- Mavko G., Mukerji T., Dvorkin J. The Rock Physics Handbook, Second Edition: Tools for Seismic Analysis of Porous Media. New York: Cambridge University Press, 2009. 524 р.
- Ranjbar A. Hassani H., Shahriar K. 3D geomechanical modeling and estimating the compaction and subsidence of Fahlian reservoir formation (X-field in SW of Iran) // Arabian Journal of Geosciences 2017. Vol. 10. № 116. P. 1-12. DOI: 10.1007/s12517-017-2906-3
- Schutjens P.M.T.M., Hanssen T.H., Hettema M.H.H. et al. Compaction-induced Porosity Permeability Reduction in Sandstone Reservoirs: Data and Model for Elasticity-Dominated Deformation // SPE Reservoir Evaluation & Engineering. 2004. Vol. 7. Iss. 3. P. 202-216. № SPE-88441-PA. DOI: 10.2118/88441-PA
- Виноградов К.Э., Пустошкин Р.В., Родионов С.П. Особенности учета гистерезиса проницаемости и сжимаемости порового пространства низкопроницаемых коллекторов при гидродинамическом моделировании // Геология, геофизика и разработка нефтяных и газовых месторождений. 2021. № 11 (359). С. 35-38. DOI: 10.33285/2413-5011-2021-11(359)-35-38
- Пантелеев И.А., Ляховский В., Мубассарова В.А. и др. Тензорная компакция пористых пород: теория и экспериментальная верификация // Записки Горного института. 2022. Т. 254. С. 234-243. DOI: 10.31897/PMI.2022.30
- Hall H.N. Compressibility of Reservoir Rocks // Journal of Petroleum Technology. 2013. Vol. 5. Iss. 01. P. 17-19. SPE-953309-G. DOI: 10.2118/953309-G
- Гасеми М.Ф., Баюк И.О. Граничные значения параметров строения пустотного пространства петроупругих моделей карбонатных пород // Физика Земли. 2020. № 2. С. 69-88. DOI: 31857/S0002333720020039
- Петраков Д.Г., Пеньков Г.М., Золотухин А.Б. Экспериментальное исследование влияния горного давления на проницаемость песчаника // Записки Горного института. 2022. Т. 254. С. 244-251. DOI: 10.31897/PMI.2022.24
- Nagel N. Compaction and subsidence issues within the petroleum industry: From Wilmington to Ekofisk and beyond // Physics and Chemistry of The Earth, Part A: Solid Earth and Geodesy. 2001. Vol. 26. Iss. 1-2. P. 3-14. DOI: 10.1016/S1464-1895(01)00015-1
- Chin L. Nagel N. Modeling of Subsidence and Reservoir Compaction under Waterflood Operations // International Journal of Geomechanics. 2004. Vol. 4. Iss. 1. P. 28-34. DOI: 10.1061/(ASCE)1532-3641(2004)4:1(28)
- Baud P., Teng-fong Wong, Wei Zhu. Effects of porosity and crack density on the compressive strength of rocks // International Journal of Rock Mechanics and Mining Sciences. 2014. Vol. P. 202-211. DOI: 10.1016/j.ijrmms.2013.08.031
- Shimin Liu, Harpalani S. Compressibility of sorptive porous media: Part 1. Background and theory // AAPG Bulletin. 2014. Vol. 98. № 9. P. 1761-1772. DOI: 10.1306/03241413133
- Jun He, Kegang Ling, Peng Pei, Xiao Ni. Calculation of rock compressibility by using the characteristics of downstream pressure change in permeability experiment // Journal of Petroleum Science and Engineering. 2016. Vol. 143. P. 121-127. DOI: 10.1016/j.petrol.2016.02.030
- Shihuai Zhang, Shunchuan Wu, Guang Zhang. Strength and deformability of a low-porosity sandstone under true triaxial compression conditions // International Journal of Rock Mechanics & Mining Sciences. 2020. Vol. 127. P. 1-13. DOI: 10.1016/j.ijrmms.2019.104204
- David E.C., Zimmerman R.W. Compressibility and shear compliance of spheroidal pores: Exact derivation via the Eshelby tensor, and asymptotic expressions in limiting cases // International Journal of Solids and Structures. 2011. Vol. 48. Iss. 5. P. 680-686. DOI: 10.1016/j.ijsolstr.2010.11.001
- Zimmerman R.W. Pore Volume and Porosity Changes under Uniaxial Strain Conditions // Transport in Porous Media. 2017. Vol. 119. P. 481-498. DOI: 10.1007/s11242-017-0894-0
- Mao Bai, Xinpu Shen, Gang Li. Alternative Method to Determine Pore Volume Compressibility Attributable to Production-Induced Reservoir Compaction // International Oil & Gas Conference and Exhibition, 8-10 June 2010, Beijing, China. P. 1-12. SPE-130212-MS. DOI: 10.2118/130212-MS
- Selvadurai A.P.S., Suvorov A.P. The influence of the pore shape on the bulk modulus and the Biot coefficient of fluid-saturated porous rocks // Scientific Reports. 2020. Vol. 10. № 18959. DOI: 10.1038/s41598-020-75979-6
- Жуков В.С., Кузьмин Ю.О. Экспериментальная оценка коэффициентов сжимаемости трещин и межзерновых пор коллектора нефти и газа // Записки Горного института. 2021. Т. 251. С. 658-666. DOI: 10.31897/PMI.2021.5.5
- Жуков В.С., Кузьмин Ю.О. Экспериментальные исследования влияния трещиноватости горных пород и модельных материалов на скорость распространения продольной волны // Физика Земли. 2020. № С.39-50. DOI: 10.31857/S0002333720040109
- Jia-Jyun Dong, Jui-Yu Hsu, Wen-JieWu et al. Stress-dependence of the permeability and porosity of sandstone and shale from TCDP Hole-A // International Journal of Rock Mechanics and Mining Sciences. 2010. Vol. 47. Iss. 7. P. 1141-1157. DOI: 10.1016/j.ijrmms.2010.06.019
- Gumrah F., Aliyev A., Guliyeva C., Ozavc O. Determining Reservoir Characteristics and Drive Mechanisms for an Oil Reservoir // SOCAR Proceedings. 2012. Iss. 4. P. 6-19. DOI: 10.5510/OGP20120400129
- Изюмов С.Ф., Кузьмин Ю.О. Исследование современных геодинамических процессов в Копетдагском регионе // Физика Земли. 2014. № С. 3-16. DOI: 10.7868/S0002333714060015
