Формирование адаптивного подхода с применением технологии машинного зрения для определения параметров осаждения продуктов обогащения
- 1 — канд. техн. наук доцент Санкт-Петербургский горный университет ▪ Orcid
- 2 — канд. техн. наук доцент Санкт-Петербургский горный университет ▪ Orcid ▪ Elibrary ▪ Scopus ▪ ResearcherID
- 3 — инженер Санкт-Петербургский горный университет ▪ Orcid
Аннотация
В работе сформирован адаптивный подход по автоматической инициализации кривой сгущения с использованием технологии машинного зрения, позволяющий с высокой точностью определять параметры материала, необходимые для проектирования сгустительных и осветлительных аппаратов. Разработано программное обеспечение, которое сделало возможным поиск координаты критической точки сгущения в автоматическом режиме. Проведенные исследования на двух пробах материалов (хвостах апатитсодержащих руд и золотосодержащего концентрата) позволили статистически доказать воспроизводимость получаемых результатов с использованием параметрических критериев Фишера и Бартлета. Установлено, что кривые осаждении с высокой точностью аппроксимируются моделью Вейбула, что в совокупности с кусочно-линейной аппроксимацией дает возможность формализовать методику определения координат критической точки. Найдены эмпирические коэффициенты модели Вейбула для двух проб, а также определены конечные разжижения и скорости осаждения исследуемых материалов.
Введение
Одним из основополагающих пунктов концепции устойчивого развития в экологическом плане является рациональное использование природных источников, обеспечивающих их пригодность как для наших современников, так и для будущих поколений [1-3]. По оценкам специалистов, около 22 % от общего водооборота используются на промышленные нужды и, по приблизительным оценкам, через три года эта цифра увеличится на 2 %.* При обогащении минерального сырья получаемые продукты содержат значительное количество воды, а также остаточные концентрации реагентов и шламовидных фракций. Правильное управление данными продуктами перед отправкой потребителю, включая их обезвоживание и размещение в дамбах, является ключевым элементом современных производств, нацеленных на соблюдение высоких экологических стандартов [4, 5]. По усредненным показателям, на обогатительных фабриках расход производственной воды на 1 т перерабатываемой руды в зависимости от типа перерабатываемого сырья, колеблется от 4 до 10 м3, а на некоторых гравитационных фабриках достигает 15 м3/т [6]. Помимо обезвоживания концентратов процессы сгущения являются ключевыми при очистке сточных вод и утилизации хвостовых продуктов. Сгущение хвостов на обогатительной фабрике позволяет организовать оборотное водоснабжение, сводя к минимуму потребность в заборе свежей воды, а также уменьшает количество воды, сбрасываемой в хвостохранилища, что, в свою очередь, снижает риск аварийных ситуаций. Все это ставит процессы обезвоживания и сгущения в один ряд с основными процессами, в значительной мере влияющими на всю технологическую цепочку [7].
Несмотря на свою значимость, процесс проектирования сгустительных и осветлительных аппаратов сводится к расчету удельной площади поверхности сгустителя по результатам проведения седиментационных исследований в статических или динамических условиях с применением методики Коу – Клевенджера, предложенной более 100 лет назад [8]. Повсеместно признанная феноменологическая модель сгущения была опубликована в конце прошлого века [9, 10] и позволила разработать программное обеспечение для проектирования и моделирования традиционных промышленных сгустителей со следующими параметрами: единица площади, профиль концентрации и запас твердого вещества в сгустителе. Но математические модели бесполезны, если недоступны экспериментальные параметры, определяющие предложенные уравнения [11].
В настоящее время выявлены проблемы, связанные с лабораторными исследованиями процесса седиментации и, прежде всего, с инициализацией и интерпретацией кривых осаждения, полученных на стадии лабораторной отработки процесса сгущения [3]. Данные проблемы связаны, по большей части, с человеческим фактором, так как качество теста напрямую зависит от опыта и компетенции исследователя. Помимо этого процесс проведения эксперимента осложнен несколькими выраженными факторами: скоротечность процесса, необходимость параллельной фиксации нескольких параметров. Для некоторых типов пульп могут возникать ситуации, при которых возможность визуального контроля и определения границы жидкость-суспензия осложняется особенностями материала, с которым ведется работа.
Решением данной проблемы занимались многие исследователи, среди наиболее значимых решений можно выделить разработанную компанией «Cettem» систему SediRack, которая независимо от оператора автоматически определяет и выдает необходимые параметры для расчета единицы площади сгущения. SediRack – это лабораторный прибор, позволяющий одновременных тестировать пять проб, каждая из которых отличается концентрацией или добавлением флокулянта (рис.1).* Высота поверхности раздела вода-суспензия измеряется автоматически в каждой пробирке с помощью видеокамеры. Зарегистрированные данные обрабатываются в режиме онлайн программой, которая выдает начальную скорость оседания в каждой из пяти пробирок. С помощью этой информации программа рассчитывает плотность твердого потока и единицу площади по методу Коу – Клевенджера для каждой исследуемой концентрации.
Однако данное ПО способно работать только с прибором, показанным на рис.1, а, что значительно ограничивает работу с данным продуктом. Аналогичная проблема свойственна и другим подобным установкам [12-14]. Между тем, современное состояние технологий позволяет реализовать подобного рода концепцию с использованием алгоритмов машинного обучения (machine learning) и компьютерного зрения (computer vision) на любом доступном испытательном стенде.
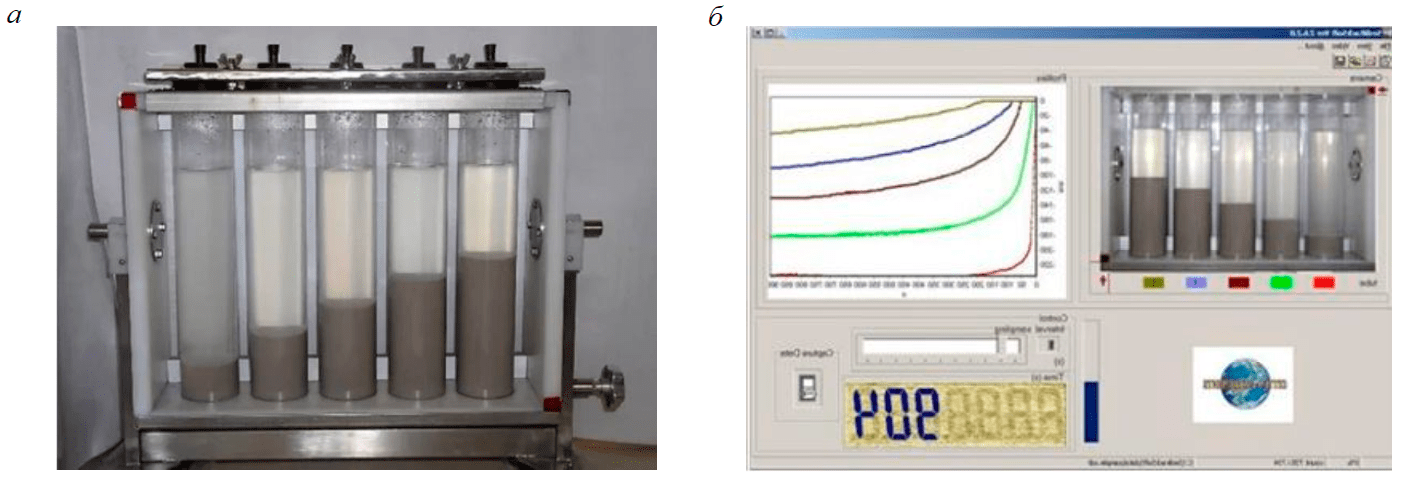
Рис.1. Установка SediRack: а – установка для определения кривых осаждения; б – диалоговое окно программы для обработки данных (en.cettem.com)
Внедрение подобных алгоритмов активно используется на обогатительных фабриках, но сфера их применения очень ограничена [15, 16]. В работе [17] авторами проанализированы исследования по данной тематике в области обогащения полезных ископаемых. Наибольшее количество работ относится к машинному зрению, что, вероятно, связано со стремлением найти косвенные методы измерения таких параметров как размер частиц или химический состав, используя изображения как более дешевую и быструю альтернативу анализу образцов. Это также может указывать на относительно широкое внедрение систем машинного зрения в промышленности, а также на исследовательскую деятельность по улучшению результатов, достигаемых с помощью систем машинного зрения. Многие из технологий, отнесенных к категории машинного зрения, являются эмпирическими моделями, связывающими параметры процесса (такие как содержание или извлечение) с характеристиками, полученными с помощью методов машинного зрения (например, размер пузырьков, частиц или статистические описания текстуры) [18-20].
В области обогащения полезных ископаемых реализованы задачи детектирования краев зерен и сегментации для обнаружения границ частиц или пузырьков и получения другой информации, такой как распределение частиц (пузырьков) по размерам, стабильность пены или даже содержание полезного компонента. Альтернативный подход включает извлечение абстрактных признаков более низкой размерности из высокоразмерных изображений; эти признаки могут коррелировать с интересующими параметрами (размер частиц или химический состав), но не измерять эти параметры напрямую.
Методы извлечения признаков тесно связаны с методами уменьшения размерности, например, анализом главных компонент. Независимо от того, используется ли подход к обработке изображений или извлечению признаков (или оба подхода), следующим шагом в применении машинного зрения является соотнесение признаков и/или параметров, полученных с изображений, с условиями процесса, переменными или ключевыми показателями эффективности, такими как сорт, химический или гранулометрический составы [17].
Целью данной работы являлась разработка адаптивного подхода с применением технологии машинного зрения для определения параметров осаждения продуктов обогащения путем автоматизации процесса фиксации данных при проведении исследований кинетики осаждения.
Методы
Для расчета требуемой площади сгустителя необходимо выполнение теста на осаждения в цилиндрах. Методика тестирования подразумевает использование прозрачных цилиндров емкостью 0,5 [21, 22], 1 [23] или 2 л [24]. В данной работе тестирование проводилось в цилиндрах емкостью 1 л, что соответствует отечественной практике [25]. Для инициализации кривой периодического осаждения цилиндр заполнялся пульпой с заданной концентрацией твердого, далее осуществлялось неинтенсивное перемешивание путем десятикратного поворота цилиндра для обеспечения полной гомогенизации пульпы с сохранением изначальных свойств оседания. В ходе стандартного теста после гомогенизации запускался таймер для отслеживания изменения положения границы раздела суспензия-жидкость через различные промежутки времени (0; 0,5; 1; 2; 3; 4; 5; 10 и более минут). Время могло быть изменено в зависимости от динамики осаждения конкретного образца осадка. Как правило, в начале испытания граница раздела суспензия-жидкость обычно измеряется чаще, поскольку осадок оседает относительно быстро. В дальнейшем частота измерений снижается, поскольку граница раздела фаз движется медленнее, скорость осаждения твердой фазы резко снижается. Наблюдение прекращали, если положение границы не изменяется в течение 2-3 ч.
При проведении данной методики возникают трудности, главной из которых является невозможность точного визуального определения границы раздела фаз. Также типичным является резкий переход из одной стадии в другую, который невозможно четко определить даже при наличии подсветки. Среди других проблем следует отметить быстротечность процессов осаждения, особенно для гравиконцентратов или сфлокулированных пульп. Механическое измерение в данном случае невозможно, как и в случае тестирования пульп без четкой границы разделения.
В данной работе для испытаний были отобраны две представительные пробы: золотосодержащий концентрат с обогатительной фабрики Олимпиаднинского месторождения насыпной плотностью 1,39 г/см3 (проба 1); хвосты переработки фабрики АНОФ-2 Кировской группы месторождений насыпной плотностью 1,19 г/см3 (проба 2) [26, 27]. Насыпная плотность определялась в соответствии с ГОСТ 25732-88. Характеристики гранулометрического состава для пробы 1: d50 = 69; d80 = 93 мкм; для пробы 2: d50 = 57,5; d80 = 87 мкм.
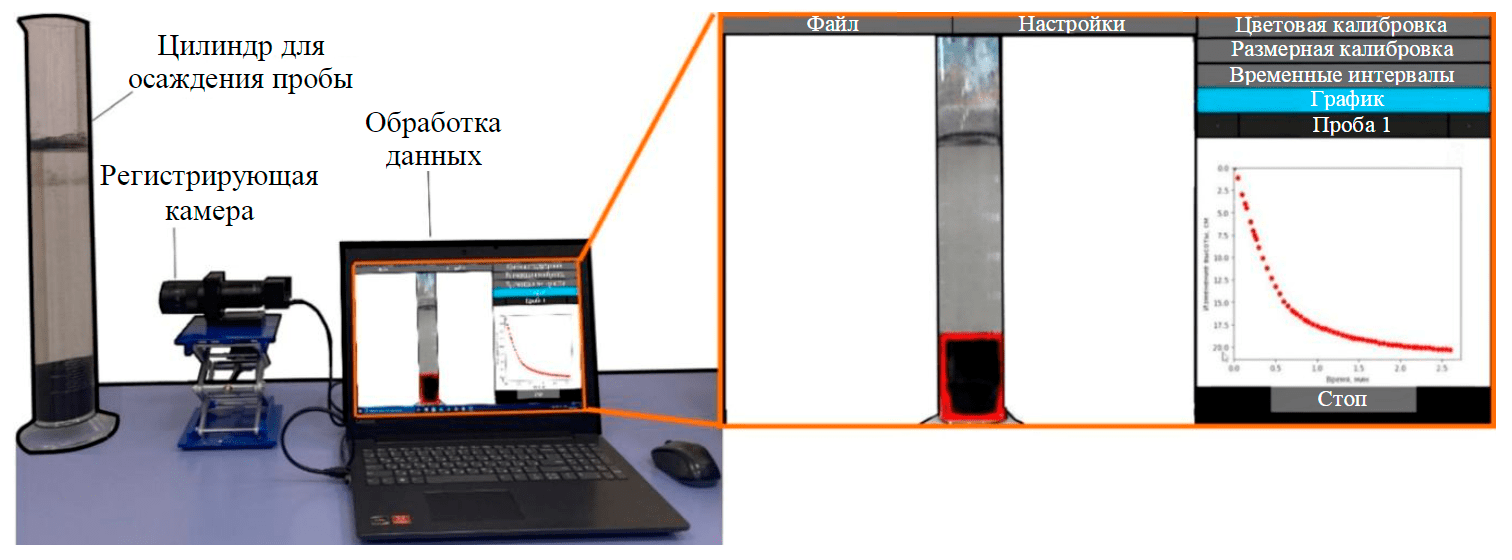
Рис.2. Опытная установка для определения кривых осаждения и интерфейс разработанного программного обеспечения
Минеральный состав пробы 1 в основном представлен арсенопиритом и пирротином (25,2 и 37,7 % соответственно), присутствуют пирит, минералы сурьмы, халькопирит, а также окислы и гидроокислы железа, содержание нерудных минералов (кварц, карбонаты, слюды, минералы Ti) около 27,7 %. В пробе 2 в значительном количестве присутствует нефелин (60,36 %), а также идентифицированы полевой шпат (7,40 %), эгирин (11,64 %), сфен, титаномагнетит, ильменит, биотит, эвдиалит и другие минералы (в совокупности менее 5 %).
Отношение Ж:Т установлено равным 5:1, в качестве флокулянта использован реагент MS-203 при расходе 100 г/т. Так как в данной работе не требовалось установить зависимость скорости осаждения от содержания твердого и выбрать наиболее подходящий флокулянт, данные показатели были выбраны по итогам предварительных испытаний для повышения скорости осаждения с целью проверки возможностей системы обработки данных при высокой скорости осаждения.
Автоматическая система контроля перемещения границы раздела фаз состояла из камеры для фиксации процесса осаждения и блока обработки информации с установленным программным обеспечением (рис.2). Предварительные тесты системы показали, что удовлетворительные результаты достигаются при разрешении камеры от двух мегапикселей.
Для разработки программного обеспечения был использован высокоуровневый язык программирования Python. Выбор языка обоснован его распространенностью при решении задач машинного обучения, компьютерного зрения, а также большим выбором готовых библиотек.
Обсуждение результатов
Схема работы программы для определения кривых осаждения приведена на рис.3.
При выборе метода детекции отслеживаемого объекта (уровня осветленного столба жидкости) была использована свободно распространяемая библиотека алгоритмов компьютерного зрения OpenCV. В данном случае принцип работы программы основывается на поэтапной обработке изображения посредством различных операций для выделения и поиска необходимого контура. Применение данного пакета позволяет реализовать тонкую настройку программного обеспечения в процессе работы. Поступающее с камеры изображение подвергается гауссовскому размытию для устранения шумов и мелких, не несущих функциональной нагрузки, деталей в изображении.
Главным признаком различения контуров объектов в данной программе является уровень контрастности между цветом оседающего материала и столбом осветленной жидкости. Такой подход позволяет однозначно выделить наблюдаемый столб жидкости и определить границу между осветленной жидкостью и суспензией. Определение контура происходит за счет бинаризации изображения. Критерии задания значения пикселю определяются пользователем путем установления границ интенсивностей свойств пикселя, и в случае, если пиксель обладает параметрами, находящимися в пределах установленных границ, ему присваивается значение 1, в противном случае – 0. Для удобства изображение переводится из стандартной цветовой схемы RGB (red, green, blue) более интуитивно понятную – HSB (hue, saturation, brightness), в которой цвет определяется не комбинацией трех базисных цветовых элементов, а тоном, насыщенностью и яркостью. Что позволяет калибровать изображения без использования значений цветовой палитры.
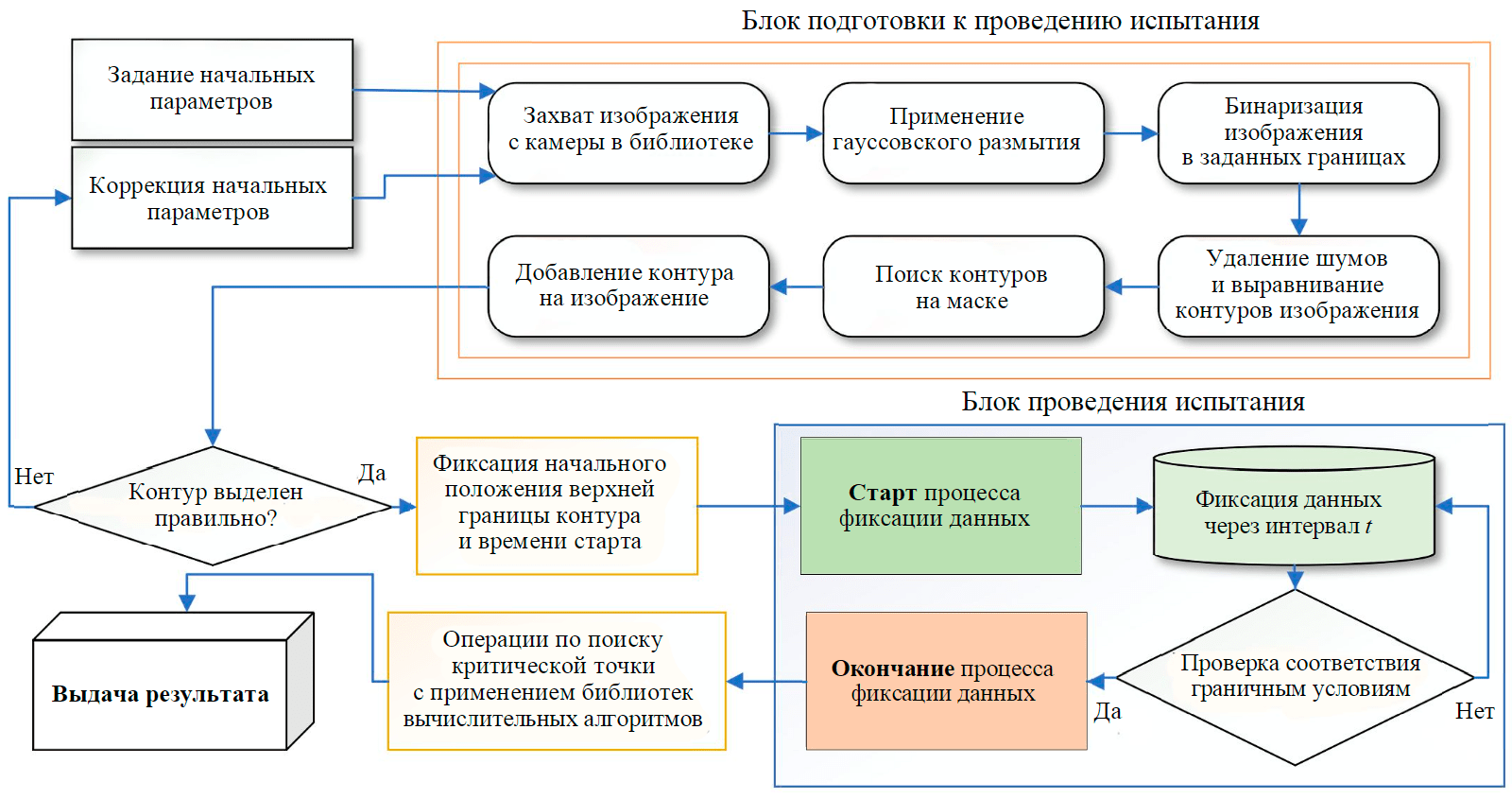
Рис.3. Алгоритм разработанного программного обеспечения

Рис.4. Маски и изображения с контуром: а – маска с неточной цветовой калибровкой; б – правильно откалиброванная маска
На следующем шаге бинаризованное изображение – маска – подвергается морфологическим преобразованиям для устранения шумов и мелких элементов, возникающих вследствие колебаний освещенности и при работе с изображением. К полученной маске последовательно применяются два алгоритма: эрозия (erosion) и дилатация (dilation). Идея эрозии заключается в следующем: квадратная матрица заданного размера с нечетным количеством элементов перебирает каждый пиксель изображения, присваивая ему значение 1 или 0 в зависимости от соответствия условию.
В случае, если центральный пиксель матрицы окружают лишь пиксели со значением 1 в пределах данной матрицы, ему также присваивается значение 1, в ином случае он приобретает значение 0. Данное преобразование позволяет удалить мелкие блики на бинаризованном изображении, делает контуры более ровными, что и требуется при определении границы между осветленной жидкостью и осажденным материалом. Однако становится очевидным, что нулевое значение приобретают пиксели и на границе крупных элементов изображения, т.е. размеры контура уменьшаются пропорционально размеру используемой в функции матрицы. Поэтому для восстановления истинных контуров объектов применяется метод дилатации с противоположным принципом работы. Матрица того же размера, обходя пиксели изображения, устанавливает в точке значение 1, если хотя бы один из пикселей в матрице равен 1. Таким образом увеличивается размер белых областей, т.е. восстанавливается истинный размер наблюдаемого объекта, а за счет предварительного удаления шумов увеличения площади шумов на изображении не наблюдается (рис.4).
В программе разработки также решена проблема поиска контура с наибольшей площадью (в случае, если контуров на изображении несколько). Так как контуры представляют собой непрерывную замкнутую кривую, проходящую по границе черной и белой областей, фактически производится поиск белого объекта на черном фоне. Полученный массив контуров сортируется в порядке уменьшения выделяемой площади, и для дальнейшего отслеживания передается только первый контур, представляющий столб пульпы. Полученный контур вписывается в прямоугольник, верхнее ребро которого в последующем используется для отслеживания положения искомой границы. Для удобства восприятия пользователем найденные контуры переносятся на цветное изображение (рис.4).
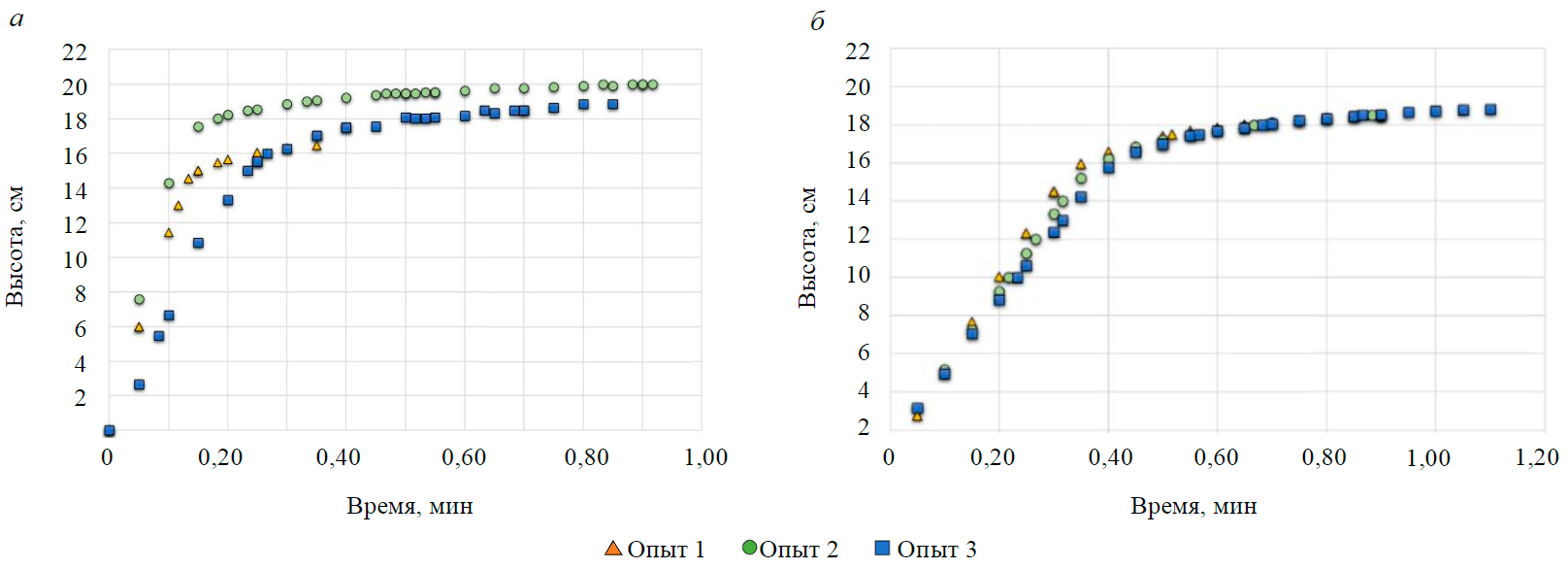
Рис.5. Инициализированные кривые осаждения для проб 1 (а) и 2 (б)
С целью проверки воспроизводимости результатов для каждой пробы опыт повторялся три раза. Полученные наборы точек для каждого из опытов для проб 1 и 2 приведены на рис.5.
Регрессионный анализ полученных данных позволил установить, что для всех проб по всем опытам наиболее подходящей является аппроксимирующая модель Вейбула (Weibull Model) такого вида [28-31]:
где h – высота осветленного слоя, см; t – время осаждения, мин; a, b, c, d – эмпирические коэффициенты (см. таблицу).
Эмпирические коэффициенты модели Вейбула
|
Номер опыта |
Эмпирические коэффициенты |
Коэффициент |
Стандартная ошибка |
|||
|
a |
b |
c |
d |
|||
|
Проба 1 |
||||||
|
1 |
16,29 |
16,27 |
43,37 |
1,52 |
0,9974 |
0,30 |
|
2 |
19,60 |
19,71 |
19,85 |
1,21 |
0,9932 |
0,35 |
|
3 |
18,36 |
18,58 |
12,68 |
1,41 |
0,9972 |
0,28 |
|
Проба 2 |
||||||
|
1 |
18,33 |
18,65 |
8,20 |
1,40 |
0,9976 |
0,35 |
|
2 |
18,56 |
18,40 |
6,44 |
1,36 |
0,9961 |
0,39 |
|
3 |
18,76 |
18,08 |
5,67 |
1,36 |
0,9964 |
0,34 |
Статистический анализ по трем выборкам, проведенный с помощью параметрического критерия Фишера и Бартлета [32-34], показал статистическое равенство дисперсий по трем опытам. Это означает, что различие в данных по пробам объясняются лишь случайными причинами. Следовательно, программа обрабатывает результаты верно, и это статистически доказано. Поэтому за истинную кривую далее принималась усредненная по результатам проведенных замеров.
В основе большинства используемых на практике методик расчета сгустителей (методы Кинча, Бискайя-мл., Талмеджа и Фитча, Робертса, Коу – Клевенджера и Олтмана [35, 36]) лежит нахождение так называемой критической точки, которая является переходной от фазы осаждения к фазе сжатия осадка. В этот момент определяют объем суспензии (по градуировке цилиндра), hкр и tкр, а также отношение Ж:Т в этот момент, которое принимают за конечное. Дальнейшее сгущение суспензии считается нецелесообразным, так как уплотнение суспензии происходит очень медленно.
Координаты критической точки определяются графическим методом, что вызывает погрешности и не может считаться достоверным результатом. Для решения данной проблемы при обработке полученных данных предложено использовать совокупность модели Вейбула и кусочно-линейной аппроксимации. В предложенном подходе выполняется следующая последовательность действий:
- Последовательность точек, зафиксированных в ходе эксперимента, аппроксимируется кусочно-линейной функцией. Для максимального захвата областей осаждения и сжатия осадка аппроксимирующие прямые выбираются автоматически. После кусочно-линейной аппроксимации возвращаются данные о точке пересечения линейных функций, а также их угловые коэффициенты.
- Полученные угловые коэффициенты используются для определения углов поворотов прямых посредством вычисления арктангенса и определения угла поворота биссектрисы. Угол между осью абсцисс и биссектрисой вычисляется посредством сложения углов двух пресекающихся в точке прямых, вычитания величины π и деления полученного результата на 2. Число π прибавляется к сумме, так как значения углов при вычислении находятся в пределах от −π/2 до π/2,
а искомая биссектриса должна иметь угол в диапазоне от 0 до −π/2. По рассчитанной величине угла определяется уравнение биссектрисы. - Та же последовательность точек аппроксимируется непрерывной функцией.
- С помощью уравнения биссектрисы и найденной функции Вейбула можно найти координаты точки их пересечения, которая и будет являться искомой критической точкой.
Обработка усредненных кривых (по высоте осевшего слоя) приведена на рис.6.
Конечное (или критическое) разжижение (отношение Ж:Т по объему) в момент tкр, исходя из найденных координат критической точки, может быть определено таким образом:
где R – радиус используемого при осаждении цилиндра, м; Mт – масса твердого в пульпе, кг; ρ, Δ – плотность твердой и жидкой фаз соответственно, кг/м3.
Удельная скорость осаждения в критической точке для проб
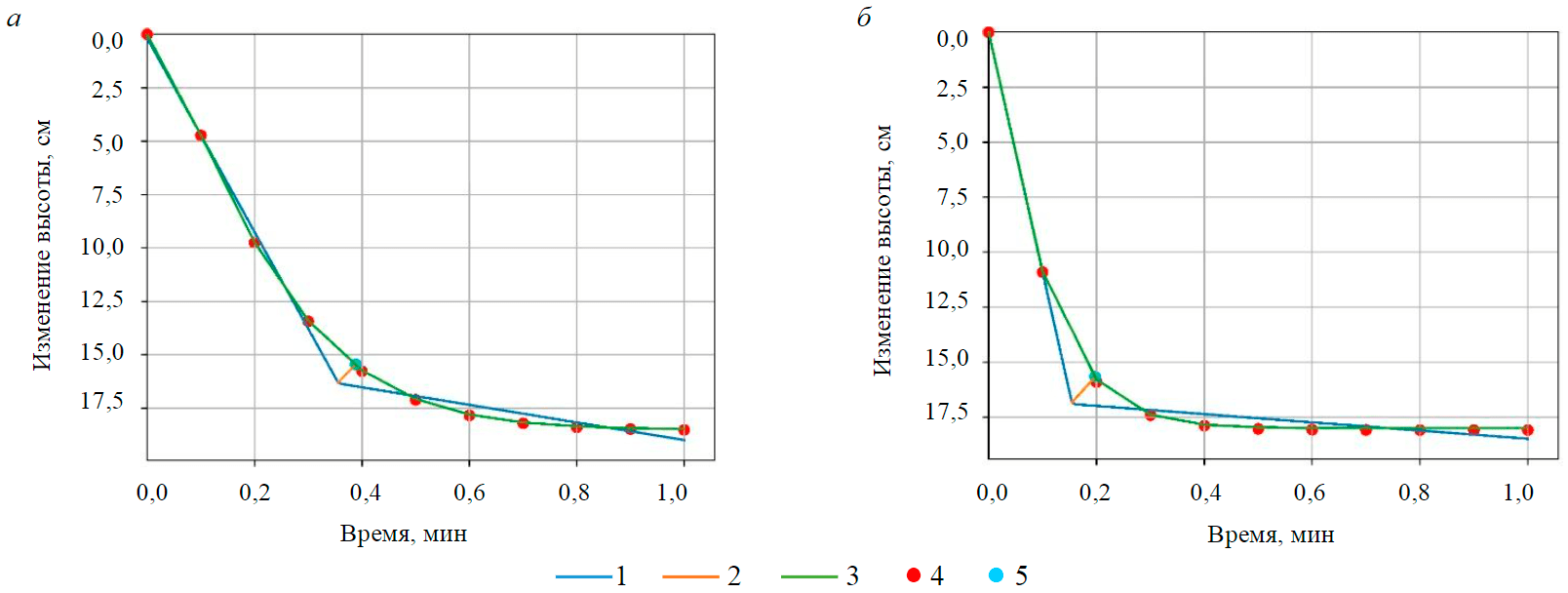
Рис.6. Результаты определения координат критической точки для проб 1 (а) и 2 (б) 1 – кусочно-линейная аппроксимация; 2 – биссектриса; 3 – аппроксимация функцией Вейбула; 4 – опытные данные; 5 – критическая точка
Результаты расчетов параметров сгущаемости пробы 1: tкр 0,39 мин; hкр 15,37 см; Rкр 1,46 см; νкр 39,41 см/мин; пробы 2: tкр 0,20 мин; hкр 15,67 см; Rкр 1,49 см; νкр 78,35 см/мин.
Для ускорения процесса как правило конечное разжижение поддерживают выше критического значения, для чего вместо критической точки может быть определена точка на кривой, соответствующая требуемому разжижению. Тогда задаваясь требуемым разжижением, рассчитывается значение h.
Заключение
В результате проведенного исследования предложено автоматизированное программное решение с использованием технологии машинного зрения для проведения теста в цилиндрах и расчета основных параметров при проектировании сгустительных и осветлительных аппаратов. Возможность тонкой настройки под конкретные условия проведения испытаний позволяет обойтись без специализированного оборудования.
Установлено, что полученные кривые осаждения аппроксимируются моделью Вейбула, применение которой в совокупности с кусочно-линейной аппроксимацией позволяет с достаточной точностью находить координаты критической точки и иных параметров.
Несмотря на отсутствие единого подхода к проектированию аппаратов для гравитационного осаждения тест на осаждения в цилиндрах де-факто является общепризнанным и в большей мере зависит от опыта и квалификации исследователя. Разработанное программное обеспечение и методический подход к расчету позволяют свести к минимуму человеческий фактор и получить достоверные результаты.
Проведенные исследования доказывают, что предложенное решение способно фиксировать данные даже при высокой скорости осаждения. При исследовании пульп без четкой границы разделения заложенные в блок обработки алгоритмы за счет морфологических операций вычитания фона позволяют фиксировать малейшие изменения в цветовой гамме и определять границу раздела фаз.
Технологии машинного зрения для обогатительных процессов переживают этап бурного развития, и данный пример показывает только один из возможных путей развития. Предложенный подход после соответствующей адаптации может быть применен для тестирования новых видов флокулянтов и коагулянтов без проведения полномасштабных испытаний, что является актуальным в условиях дефицита некоторых видов реагентов. Данная область применения не является единственной, а подход может быть адаптирован для контроля фаз пена-пульпа во флотационном обогащении, а также при исследовании различных руд на обогатимость.
*Проскурякова Л.Н., Саритас О., Сиваев С.Б. Водохозяйственный комплекс: глобальные вызовы и долгосрочные тенденции инновационного развития. М.: Национальный исследовательский университет «Высшая школа экономики», 2015. 84 с.
Литература
- Litvinenko V., Bowbriсk I., Naumov I., Zaitseva Z. Global guidelines and requirements for professional competencies of natural resource extraction engineers: Implications for ESG principles and sustainable development goals // Journal of Cleaner Production. 2022. Vol. 338. № 130530. DOI: 10.1016/j.jclepro.2022.130530
- Romasheva N., Dmitrieva D. Energy Resources Exploitation in the Russian Arctic: Challenges and Prospects for the Sustainable Development of the Ecosystem // Energies. 2021. Vol. 14. № 8300. DOI: 10.3390/en14248300
- Бойко Н.А., Чвилева Т.А., Ромашева Н.В. Влияние деятельности угольных компаний на социально-экономическое развитие угледобывающих регионов и ее оценка // Уголь. 2019. № 11. С. 48-53. DOI: 10.18796/0041-5790-2019-11-48-53
- Diaz P., Salas J.C., Cipriano A., Núnez F. Random forest model predictive control for paste thickening // Minerals Engineering. 2021. Vol. 163. № 106760. DOI: 10.1016/j.mineng.2020.106760
- Cacciuttolo C., Holgado A. Management of Paste Tailings in Chile: A Review of Practical Experience and Environmental Acceptance // PASTE 2016 – Proceedings of the 19th International Seminar on Paste and Thickened Tailings, 5-8 July 2016, Santiago, Chile, 2016. Р. 1-15.
- Александрова Т.Н., O’Коннор С. Переработка платинометалльных руд в России и Южной Африке: состояние и перспективы // Записки Горного института. 2020. Т. 244. C. 462-473. DOI: 10.31897/PMI.2020.4.9
- Бауман А.В. Проблемные вопросы проектирования схем сгущения и водооборота обогатительных фабрик // Обогащение руд. 2016. № 3. С. 58-62.DOI: 10.17580/or.2016.03.10
- Кирнарский А.С. Уравнение Коу – Клевенджера и развитие технологии водно-шламового хозяйства углеобогатительных фабрик // Уголь Украины. 2016. № 6-7. С. 62-66.
- Concha F., Segovia J.P., Vergara S. et al. Audit industrial thickeners with new on-line instrumentation // Powder Technology. 2017. Vol. 314. P. 680-689. DOI: 10.1016/j.powtec.2017.03.040
- Betancourt F., Concha F., Uribe L. Settling velocities of particulate systems part 17. Settling velocities of individual sphe-rical particles in Power-Law non-Newtonian fluids // International Journal of Mineral Processing. 2015. Vol. 143. P. 125-130. DOI: 10.1016/j.minpro.2015.07.005
- Segovia J. P., Concha F., Sbarbaro D. On the control of sludge level and underflow concentration in industrial thickeners // 18th IFAC World Congress, 28 August – 2 September 2011, Milano, Italy. IFAC Proceedings Volumes. 2011. Vol. 44. Iss. 1. P. 8571-8576. DOI: 10.3182/20110828-6-IT-1002.02667
- Fedorova E.R., Vasileva N.V., Pupysheva E.A. Algorithm to distribute feed pulp between paralleled thickeners during red-sludge thickening and washing in alumina production // Journal of Physics: Conference Series. 2019. Vol. 1333. Iss. 4. № 042007. DOI: 10.1088/1742-6596/1333/4/042007
- Хайникке Ф., Либервирт Х., Кюнель Р., Александрова Т.Н. Преимущество селективного измельчения с помощью валковых прессов высокого давления в сочетании с пневматической классификацией // Обогащение руд. 2022. № 1. С. 3-7. DOI: 10.17580/or.2022.01.01
- Grabsch A.F., Yahyaei M., Fawell P.D. Number-sensitive particle size measurements for monitoring flocculation responses to different grinding conditions // Minerals Engineering. 2020. Vol. 145. № 106088. DOI: 10.1016/j.mineng.2019.106088
- Heras de las J.L.B., Gutiérrez-Lavín A., Mahamud-López M.M. et al. Towards a Unified Model on the Description and Design of Process Operations: Extending the concept of Separation Units to Solid-fluid Sedimentation // Recent Innovations in Chemical Engineering (Formerly Recent Patents on Chemical Engineering). 2019. Vol. 12. Iss. 1. P. 15-53. DOI: 10.2174/2405520412666181123094540
- François P., Locatelli F., Laurent J., Bekkour K. Experimental study of activated sludge batch settling velocity profile // Flow Measurement and Instrumentation. 2016. Vol. 48. P. 112-117. DOI: 10.1016/j.flowmeasinst.2015.08.009
- McCoy J.T., Auret L. Machine learning applications in minerals processing: A review // Minerals Engineering. 2019. Vol. 132. P. 95-109. DOI: 10.1016/j.mineng.2018.12.004
- Zhukovskiy Y.L., Kovalchuk M.S., Batueva D.E., Senchilo N.C. Development of an algorithm for regulating the load sche-dule of educational institutions based on the forecast of electric consumption within the framework of application of the demand response // Sustainability. 2021. Vol. 13 (24). № 13801. DOI: 10.3390/su132413801
- Машевский Г.Н., Ушаков Е.К., Яковлева Т.А. Цифровая технология оптимизации дозирования сернистого натрия при флотации медной руды // Обогащение руд. 2021. № 3. С. 18-33. DOI: 10.17580/or.2021.03.04
- Boikov A.V., Payor V.A., Savelev R.V. Technical vision system for analysing the mechanical characteristics of bulk materials // Journal of Physics: Conference Series. 2018. Vol. 944. № 012021. DOI: 10.1088/1742-6596/944/1/012021
- Bahmani-Ghaedi A., Hassanzadeh A., Sam A., Entezari-Zarandi A. The effect of residual flocculants in the circulating water on dewatering of Gol-e-Gohar iron ore // Minerals Engineering. 2022. Vol. 179. № 107440. DOI: 10.1016/j.mineng.2022.107440
- Lianfu Zhang, Hongjiang Wang, Aixiang Wu et al. A zone settling velocity function to characterize settling properties of suspensions in thickening applications // Minerals Engineering. 2022. Vol. 177. № 107386. DOI: 10.1016/j.mineng.2021.107386
- Dubey A., Patra A.S., Sarkar A.N. et al. Synthesis of a copolymeric system and its flocculation performance for iron ore tailings // Minerals Engineering. 2021. Vol. 165. № 106848. DOI: 10.1016/j.mineng.2021.106848
- Leite A.M.C., Reis É.L. Cationic starches as flocculants of iron ore tailing slime // Minerals Engineering. 2020. Vol. 148. № 106195. DOI: 10.1016/j.mineng.2020.106195
- ЧерниговД.А., БогородскийА.В., НабиулинР.Н., МинееваТ.С. Исследование процессов сгущения продук-тов обогащения золотосодержащих руд // iPolytech Journal. 2021. Т. 25. № 3. С. 391-401. DOI: 10.21285/1814-3520-2021-3-391-401
- Александрова Т.Н., Кузнецов В. В., Иванов Е. А. Исследование влияния ионов жесткости воды на флотируемость медно-никелевых руд // Горный информационно-аналитический бюллетень. 2022. № 6-1. С. 263-278. DOI: 10.25018/0236_1493_2022_61_0_263
- Гурман М.А., Александрова Т.Н., Щербак Л.И. Флотационное обогащение бедной золото- и углеродсодержащей руды // Горный журнал. № 2. С. 70-74 DOI: 10.17580/gzh.2017.02.13
- Puri S., Verma A. Color removal from secondary treated pulp & paper industry effluent using waste driven Fe–TiO2 composite // Chemosphere. 2022. Vol. 303. Part 3. № 135143. DOI: 10.1016/j.chemosphere.2022.135143
- Yugen Li, Huimei Zhang, Min Chen et al. Strength criterion of rock mass considering the damage and effect of joint dip angle // Scientific Reports. 2022. Vol. 12. № 2601. DOI: 10.1038/s41598-022-06317-1
- Xianliang Wang, Jianhai Zhang, Li Qian et al. Nonlinear statistical damage constitutive model of granite based on the energy dissipation ratio // Scientific Reports. 2022. Vol. 12. № 5460. DOI: 10.1038/s41598-022-09503-3
- Oliveira Ferreira de D.J., Mattos Fiuza de M.P., Cardoso M., Oliveira de I.M. Use of the Weibull model on sizing thickeners – Part I: Sedimentation curve representation // The Canadian Journal of Chemical Engineering. 2021. Vol. 99. Iss. 3. P. 708-724. DOI: 10.1002/cjce.23904
- Larsson R. Bartlett correction of an independence test in a multivariate Poisson model // Statistica Neerlandica. 2022. P. 1-27. DOI: 10.1111/stan.12265
- Sorokina I.I., Astahov M.V., Slavkina E.V. Statistical Analysis of Test Results of Metal-Composite Compounds Under Action of Shear // International Conference on Industrial Engineering. Springer, Cham, 2021. P. 456-463. DOI: 10.1007/978-3-030-54814-8_54
- Cavalcanti A.B., Botter D.A., Barroso L.P. et al. Improved score tests for exponential family nonlinear models // Communications in Statistics – Theory and Methods. 2021. Vol. 50. Iss. 15. P. 3731-3745. DOI: 10.1080/03610926.2019.1710202
- Oliveira Ferreira de D.J., Galery R.,Cardoso M., Oliveira de I.M. Use of the Weibull model on sizing thickeners – Part II: Methods of thickener sizing // The Canadian Journal of Chemical Engineering. 2021. Vol. 99. Iss. 3. P. 708-724. DOI: 10.1002/cjce.24438
- Aixiang Wu, Zhuen Ruan, Jiandong Wang. Rheological behavior of paste in metal mines // International Journal of Minerals, Metallurgy and Materials. 2022. Vol. 29. № 4. P. 717-726. DOI: 10.1007/s12613-022-2423-6
