ąĀą░ąĘčĆą░ą▒ąŠčéą║ą░ ąĮąŠą▓ąŠą╣ č乊čĆą╝čāą╗čŗ ą┤ą╗čÅ čĆą░čüč湥čéą░ čéčĆąĄą▒čāąĄą╝ąŠą╣ č鹊ą╗čēąĖąĮčŗ ą╗ąĄą┤ąŠą┐ąŠčĆąŠą┤ąĮąŠą│ąŠ ąŠą│čĆą░ąČą┤ąĄąĮąĖčÅ ą┐ąŠ čāčüą╗ąŠą▓ąĖčÄ ą┐čĆąŠčćąĮąŠčüčéąĖ
- 1 ŌĆö ą┤-čĆ č鹥čģąĮ. ąĮą░čāą║ ąĘą░ą▓ąĄą┤čāčÄčēąĖą╣ ą╗ą░ą▒ąŠčĆą░č鹊čĆąĖąĄą╣ ąōąŠčĆąĮčŗą╣ ąĖąĮčüčéąĖčéčāčé ąŻčĆą× ąĀąÉąØ Ō¢¬ Orcid
- 2 ŌĆö ą┤-čĆ č鹥čģąĮ. ąĮą░čāą║ ąĘą░ą▓ąĄą┤čāčÄčēąĖą╣ ąŠčéą┤ąĄą╗ąŠą╝ ąōąŠčĆąĮčŗą╣ ąĖąĮčüčéąĖčéčāčé ąŻčĆą× ąĀąÉąØ Ō¢¬ Orcid Ō¢¬ Scopus
ąÉąĮąĮąŠčéą░čåąĖčÅ
ąśčüčüą╗ąĄą┤ąŠą▓ą░ąĮą░ ąĘą░ą┤ą░čćą░ ąŠą▒ čāą┐čĆčāą│ąŠą┐ą╗ą░čüčéąĖč湥čüą║ąŠą╝ ą┤ąĄč乊čĆą╝ąĖčĆąŠą▓ą░ąĮąĖąĖ ą╗ąĄą┤ąŠą┐ąŠčĆąŠą┤ąĮąŠą│ąŠ ąŠą│čĆą░ąČą┤ąĄąĮąĖčÅ (ąøą¤ą×) čü ąĮąĄąŠą│čĆą░ąĮąĖč湥ąĮąĮąŠą╣ ą▓čŗčüąŠč鹊ą╣ ąĘą░čģąŠą┤ą║ąĖ, ą▓ą┐ąĄčĆą▓čŗąĄ čüč乊čĆą╝čāą╗ąĖčĆąŠą▓ą░ąĮąĮą░čÅ ąĪ.ąĪ.ąÆčÅą╗ąŠą▓čŗą╝. ą¤čĆąŠą░ąĮą░ą╗ąĖąĘąĖčĆąŠą▓ą░ąĮčŗ ą┐ąŠą╗čÅ ąĮą░ą┐čĆčÅąČąĄąĮąĖą╣ ąĖ ą┐ąĄčĆąĄą╝ąĄčēąĄąĮąĖą╣, ą▓ąŠąĘąĮąĖą║ą░čÄčēąĖčģ ą▓ ąøą¤ą× ą▓ čĆąĄąĘčāą╗čīčéą░č鹥 ą┐čĆąĖą╗ąŠąČąĄąĮąĖčÅ ą▓ąĮąĄčłąĮąĖčģ ąĮą░ą│čĆčāąĘąŠą║ ą┤ą╗čÅ ąĮąĄčüą║ąŠą╗čīą║ąĖčģ ą┐ąŠą│čĆą░ąĮąĖčćąĮčŗčģ čüąĖčéčāą░čåąĖą╣ ŌĆō ąĘą░čĆąŠąČą┤ąĄąĮąĖčÅ ąĘąŠąĮčŗ ą┐ą╗ą░čüčéąĖč湥čüą║ąĖčģ ą┤ąĄč乊čĆą╝ą░čåąĖą╣ ąĖ čĆą░čüą┐čĆąŠčüčéčĆą░ąĮąĄąĮąĖčÅ čŹč鹊ą╣ ąĘąŠąĮčŗ ąĮą░ ą▓čüčÄ č鹊ą╗čēąĖąĮčā ąøą¤ą×. ąĀą░čüą┐čĆąŠčüčéčĆą░ąĮąĄąĮąĖąĄ ąĘąŠąĮčŗ ą┐ą╗ą░čüčéąĖč湥čüą║ąĖčģ ą┤ąĄč乊čĆą╝ą░čåąĖą╣ čüąŠąŠčéą▓ąĄčéčüčéą▓čāąĄčé ą┐čĆąĄą┤ąĄą╗čīąĮąŠą╝čā čĆą░ą▓ąĮąŠą▓ąĄčüąĖčÄ ąøą¤ą×, ą┤ą╗čÅ ą║ąŠč鹊čĆąŠą│ąŠ ąĪ.ąĪ.ąÆčÅą╗ąŠą▓ ą▓čŗą▓ąĄą╗ č乊čĆą╝čāą╗čā č鹊ą╗čēąĖąĮčŗ ąøą¤ą× ą┐ąŠ čāčüą╗ąŠą▓ąĖčÄ ą┐čĆąŠčćąĮąŠčüčéąĖ. ą¤ąŠą╗čāč湥ąĮąĮčŗąĄ čĆąĄąĘčāą╗čīčéą░čéčŗ ą┐ąŠčüą╗čāąČąĖą╗ąĖ ąŠčéą┐čĆą░ą▓ąĮąŠą╣ č鹊čćą║ąŠą╣ ą┤ą╗čÅ ą┐ąĄčĆąĄčģąŠą┤ą░ ąŠčé ąŠą┤ąĮąŠą╝ąĄčĆąĮąŠą╣ ą║ ą┤ą▓čāčģą╝ąĄčĆąĮąŠą╣ ąĘą░ą┤ą░č湥 ąŠ ą┤ąĄč乊čĆą╝ąĖčĆąŠą▓ą░ąĮąĖąĖ ąøą¤ą× čü ą║ąŠąĮąĄčćąĮąŠą╣ ą▓čŗčüąŠč鹊ą╣ ąĘą░čģąŠą┤ą║ąĖ. ą¤čĆąŠą▓ąĄą┤ąĄąĮąŠ čćąĖčüą╗ąĄąĮąĮąŠąĄ ą╝ąŠą┤ąĄą╗ąĖčĆąŠą▓ą░ąĮąĖąĄ ą┤ąĄč乊čĆą╝ąĖčĆąŠą▓ą░ąĮąĖčÅ ąøą¤ą× ą┐čĆąĖ ą┐ąŠą╝ąŠčēąĖ ą¤ą× FreeFEM++ ą▓ ą┤ą▓čāčģą╝ąĄčĆąĮąŠą╣ ąŠčüąĄčüąĖą╝ą╝ąĄčéčĆąĖčćąĮąŠą╣ ą┐ąŠčüčéą░ąĮąŠą▓ą║ąĄ ŌĆō ą▓ čĆą░ą╝ą║ą░čģ ą┤ą▓čāčģ čĆą░čüč湥čéąĮčŗčģ čüčģąĄą╝ čü čĆą░ąĘą╗ąĖčćąĮčŗą╝ąĖ ą│čĆą░ąĮąĖčćąĮčŗą╝ąĖ čāčüą╗ąŠą▓ąĖčÅą╝ąĖ ąĮą░ ą▓ąĄčĆčģąĮąĄą╝ č鹊čĆčåąĄ ąøą¤ą×. ąÆ ą┐ąĄčĆą▓ąŠą╣ čüčģąĄą╝ąĄ čäąĖą║čüąĖčĆąŠą▓ą░ą╗ąĖčüčī ą║ą░ą║ ą▓ąĄčĆčéąĖą║ą░ą╗čīąĮčŗąĄ, čéą░ą║ ąĖ čĆą░ą┤ąĖą░ą╗čīąĮčŗąĄ ą┐ąĄčĆąĄą╝ąĄčēąĄąĮąĖčÅ ąĮą░ ą▓čüąĄą╝ ą▓ąĄčĆčģąĮąĄą╝ č鹊čĆčåąĄ, ą░ ą▓ąŠ ą▓č鹊čĆąŠą╣ čüčģąĄą╝ąĄ ąĮą░ ą▓ąĄčĆčģąĮąĄą╝ č鹊čĆčåąĄ ąĘą░ą┤ą░ą▓ą░ą╗ą░čüčī ą▓ąĄčĆčéąĖą║ą░ą╗čīąĮą░čÅ ąĮą░ą│čĆčāąĘą║ą░, čüąŠąŠčéą▓ąĄčéčüčéą▓čāčÄčēą░čÅ ą▓ąĄčüčā ą▓čŗčłąĄą╗ąĄąČą░čēąĖčģ ą┐ąŠčĆąŠą┤. ą¤ąŠ čĆąĄąĘčāą╗čīčéą░čéą░ą╝ ąĖčüčüą╗ąĄą┤ąŠą▓ą░ąĮąĖą╣ ą┐čĆąĄą┤ą╗ąŠąČąĄąĮą░ ą╝ąŠą┤ąĖčäąĖą║ą░čåąĖčÅ č乊čĆą╝čāą╗čŗ ąĪ.ąĪ.ąÆčÅą╗ąŠą▓ą░, ąŠčüąĮąŠą▓ą░ąĮąĮą░čÅ ąĮą░ ą║čĆąĖč鹥čĆąĖąĖ ą┐čĆąŠčćąĮąŠčüčéąĖ ą£ąŠčĆą░ ŌĆō ąÜčāą╗ąŠąĮą░ ąĖ ą▓ą║ą╗čÄčćą░čÄčēą░čÅ ą▓ čüąĄą▒čÅ ąĮąŠą▓čŗą╣ ą┐ą░čĆą░ą╝ąĄčéčĆ ŌĆō ą▓čŗčüąŠčéčā ąĘą░čģąŠą┤ą║ąĖ. ąöą╗čÅ čĆą░ąĘą╗ąĖčćąĮčŗčģ čüą╗ąŠąĄą▓ ą┐ąŠčĆąŠą┤ ąŠą┐čĆąĄą┤ąĄą╗ąĄąĮčŗ čāčüą╗ąŠą▓ąĖčÅ, ą┐čĆąĖ ą║ąŠč鹊čĆčŗčģ ą║ąŠąĮąĄčćąĮą░čÅ ą▓čŗčüąŠčéą░ ąĘą░čģąŠą┤ą║ąĖ ąĮąĄ ąŠą║ą░ąĘčŗą▓ą░ąĄčé ąĘąĮą░čćąĖč鹥ą╗čīąĮąŠą│ąŠ ą▓ą╗ąĖčÅąĮąĖčÅ ąĮą░ čĆą░čüč湥čéąĮčāčÄ č鹊ą╗čēąĖąĮčā ąøą¤ą×, čćč鹊 ą┐ąŠąĘą▓ąŠą╗čÅąĄčé ą┐čĆąĖą╝ąĄąĮčÅčéčī ą║ą╗ą░čüčüąĖč湥čüą║čāčÄ č乊čĆą╝čāą╗čā ąĪ.ąĪ.ąÆčÅą╗ąŠą▓ą░ ą┤ą╗čÅ čĆą░čüč湥čéą░ č鹊ą╗čēąĖąĮčŗ ąøą¤ą× ą┐ąŠ čāčüą╗ąŠą▓ąĖčÄ ą┐čĆąŠčćąĮąŠčüčéąĖ, ą┐čĆąĄą┤ą┐ąŠą╗ą░ą│ą░čÅ ąĮąĄąŠą│čĆą░ąĮąĖč湥ąĮąĮčāčÄ ą▓čŗčüąŠčéčā ąĘą░čģąŠą┤ą║ąĖ.
ążąĖąĮą░ąĮčüąĖčĆąŠą▓ą░ąĮąĖąĄ
ąĀą░ą▒ąŠčéą░ ą▓čŗą┐ąŠą╗ąĮąĄąĮą░ ą┐čĆąĖ čäąĖąĮą░ąĮčüąŠą▓ąŠą╣ ą┐ąŠą┤ą┤ąĄčƹȹ║ąĄ ą£ąĖąĮąĖčüč鹥čĆčüčéą▓ą░ ą▓čŗčüčłąĄą│ąŠ ąŠą▒čĆą░ąĘąŠą▓ą░ąĮąĖčÅ ąĖ ąĮą░čāą║ąĖ ąĀąż ą▓ čĆą░ą╝ą║ą░čģ ą┐čĆąŠąĄą║čéą░ Ōä¢ 122030100425-6.
ąÆą▓ąĄą┤ąĄąĮąĖąĄ
ąĪčéčĆąŠąĖč鹥ą╗čīčüčéą▓ąŠ čłą░čģčéąĮčŗčģ čüčéą▓ąŠą╗ąŠą▓ ą▓ ąŠą▒ą▓ąŠą┤ąĮąĄąĮąĮčŗčģ ąĖ ąĮąĄčāčüč鹊ą╣čćąĖą▓čŗčģ ą┐ąŠčĆąŠą┤ą░čģ ąŠą▒čŗčćąĮąŠ ąŠčüčāčēąĄčüčéą▓ą╗čÅąĄčéčüčÅ čĆą░ąĘą╗ąĖčćąĮčŗą╝ąĖ čüą┐ąŠčüąŠą▒ą░ą╝ąĖ [1, 2]. ąÆ ą║ą░ą╗ąĖą╣ąĮčŗčģ čĆčāą┤ąĮąĖą║ą░čģ ąĖčüą┐ąŠą╗čīąĘčāąĄčéčüčÅ čüą┐ąŠčüąŠą▒ ąĖčüą║čāčüčüčéą▓ąĄąĮąĮąŠą│ąŠ ąĘą░ą╝ąŠčĆą░ąČąĖą▓ą░ąĮąĖčÅ ą┐ąŠčĆąŠą┤, čćč鹊 čüą▓čÅąĘą░ąĮąŠ čü ąŠčüąŠą▒ąĄąĮąĮąŠčüčéčÅą╝ąĖ ą╝ąĄčüč鹊čĆąŠąČą┤ąĄąĮąĖą╣ ŌĆō ą▓ąŠą┤ąŠčĆą░čüčéą▓ąŠčĆąĖą╝ąŠčüčéčīčÄ čĆčāą┤ ąĖ ąĮąĄąŠą▒čģąŠą┤ąĖą╝ąŠčüčéčīčÄ ąĘą░čēąĖčéčŗ ą│ąŠčĆąĮčŗčģ ą▓čŗčĆą░ą▒ąŠč鹊ą║ ąŠčé ą┐čĆąŠąĮąĖą║ąĮąŠą▓ąĄąĮąĖčÅ ą┐ąŠą┤ąĘąĄą╝ąĮčŗčģ ą▓ąŠą┤ [3, 4]. ą¤čāč鹥ą╝ ąĖčüą║čāčüčüčéą▓ąĄąĮąĮąŠą│ąŠ ąĘą░ą╝ąŠčĆą░ąČąĖą▓ą░ąĮąĖčÅ ą┐ąŠčĆąŠą┤ čüąŠąĘą┤ą░ąĄčéčüčÅ ą╗ąĄą┤ąŠą┐ąŠčĆąŠą┤ąĮąŠąĄ ąŠą│čĆą░ąČą┤ąĄąĮąĖąĄ (ąøą¤ą×), ąŠą▒ąĄčüą┐ąĄčćąĖą▓ą░čÄčēąĄąĄ ą│ąĖą┤čĆąŠąĖąĘąŠą╗čÅčåąĖčÄ čüčéčĆąŠčÅčēąĄą╣čüčÅ ą│ąŠčĆąĮąŠą╣ ą▓čŗčĆą░ą▒ąŠčéą║ąĖ ąĖ ą┤ąŠą┐ąŠą╗ąĮąĖč鹥ą╗čīąĮąŠąĄ čāą┐čĆąŠčćąĮąĄąĮąĖąĄ ąĄąĄ ąĮąĄąĘą░ą║čĆąĄą┐ą╗ąĄąĮąĮčŗčģ čüč鹥ąĮąŠą║. ąøą¤ą× ą┤ąŠą╗ąČąĮąŠ ąĖą╝ąĄčéčī ą┤ąŠčüčéą░č鹊čćąĮčāčÄ č鹊ą╗čēąĖąĮčā, ąŠą┐čĆąĄą┤ąĄą╗čÅąĄą╝čāčÄ čāčüą╗ąŠą▓ąĖčÅą╝ąĖ ą┐čĆąŠčćąĮąŠčüčéąĖ ąĖ ą┐ąŠą╗ąĘčāč湥čüčéąĖ ą┐ąŠčĆąŠą┤ [5-7].
ąöąĄą╣čüčéą▓čāčÄčēąĖą╝ąĖ ąĮąŠčĆą╝ą░čéąĖą▓ąĮčŗą╝ąĖ ą░ą║čéą░ą╝ąĖ (ąĪą¤ 248.1325800.2016, ąĪąØąĖą¤ 32-02-2003) čāčüčéą░ąĮą░ą▓ą╗ąĖą▓ą░ąĄčéčüčÅ, čćč鹊 ą┐čĆąŠąĄą║čéąĖčĆąŠą▓ą░ąĮąĖąĄ čüą┐ąĄčåąĖą░ą╗čīąĮčŗčģ čüą┐ąŠčüąŠą▒ąŠą▓ ą┐čĆąŠčģąŠą┤ą║ąĖ ą┐ąŠą┤ąĘąĄą╝ąĮčŗčģ čüąŠąŠčĆčāąČąĄąĮąĖą╣ čüą╗ąĄą┤čāąĄčé ą▓čŗą┐ąŠą╗ąĮčÅčéčī ą▓ čüąŠąŠčéą▓ąĄčéčüčéą▓ąĖąĖ čü ąĖąĮčüčéčĆčāą║čåąĖąĄą╣ ąÆąĪąØ 189-78, ą▓ ą║ąŠč鹊čĆąŠą╣ ą┐čĆąĄą┤ą╗ąŠąČąĄąĮčŗ ą┐čĆąŠčüčéčŗąĄ čĆą░čüč湥čéąĮčŗąĄ č乊čĆą╝čāą╗čŗ č鹊ą╗čēąĖąĮčŗ ąøą¤ą× ą┐ąŠ čāčüą╗ąŠą▓ąĖčÄ ą┐čĆąŠčćąĮąŠčüčéąĖ ŌĆō č乊čĆą╝čāą╗ą░ ąøčÅą╝ąĄ ŌĆō ąōą░ą┤ąŠą╗ąĖąĮą░ ąĖ č乊čĆą╝čāą╗ą░ ąöąŠą╝ą║ąĄ. ążąŠčĆą╝čāą╗ą░ ąøčÅą╝ąĄ ŌĆō ąōą░ą┤ąŠą╗ąĖąĮą░ čāčćąĖčéčŗą▓ą░ąĄčé č鹊ą╗čīą║ąŠ čāą┐čĆčāą│ąŠąĄ ą┤ąĄč乊čĆą╝ąĖčĆąŠą▓ą░ąĮąĖąĄ ąøą¤ą× ąĖ ą┐čĆąĖą╝ąĄąĮčÅąĄčéčüčÅ ą┐čĆąĖ ą╝ą░ą╗čŗčģ ąĮą░ą│čĆčāąĘą║ą░čģ, ą▓ č鹊 ą▓čĆąĄą╝čÅ ą║ą░ą║ č乊čĆą╝čāą╗ą░ ąöąŠą╝ą║ąĄ čćą░čüčéąĖčćąĮąŠ čāčćąĖčéčŗą▓ą░ąĄčé čāą┐čĆčāą│ąŠą┐ą╗ą░čüčéąĖč湥čüą║ąŠąĄ ą┤ąĄč乊čĆą╝ąĖčĆąŠą▓ą░ąĮąĖąĄ ąĖ ą┐čĆąĖą╝ąĄąĮąĖą╝ą░ ą▓ ą▒ąŠą╗ąĄąĄ čłąĖčĆąŠą║ąŠą╝, ąĮąŠ ą┐ąŠ-ą┐čĆąĄąČąĮąĄą╝čā ąŠą│čĆą░ąĮąĖč湥ąĮąĮąŠą╝ ą┤ąĖą░ą┐ą░ąĘąŠąĮąĄ ąĮą░ą│čĆčāąĘąŠą║ [8]. ąÆ čŹčéąĖčģ č乊čĆą╝čāą╗ą░čģ ąĖčüą┐ąŠą╗čīąĘčāąĄčéčüčÅ čāčüą╗ąŠą▓ąĖąĄ ą┐ą╗ą░čüčéąĖčćąĮąŠčüčéąĖ ąóčĆąĄčüą║ą░ ŌĆō ąĪąĄąĮ-ąÆąĄąĮą░ąĮą░ [9, 10], ą║ąŠč鹊čĆąŠąĄ ą┐ą╗ąŠčģąŠ ą┐čĆąĖą╝ąĄąĮąĖą╝ąŠ ą║ ąĘą░ą╝ąŠčĆąŠąČąĄąĮąĮčŗą╝ ą┐ąŠčĆąŠą┤ą░ą╝ [11]. ąæąŠą╗ąĄąĄ ą║ąŠčĆčĆąĄą║čéąĮčŗą╣ ą░ąĮą░ą╗ąĖąĘ ąŠčüąŠą▒ąĄąĮąĮąŠčüč鹥ą╣ ą┐ąĄčĆąĄčģąŠą┤ą░ ą▓ ąĘąŠąĮčā ą┐ą╗ą░čüčéąĖč湥čüą║ąŠą│ąŠ ą┤ąĄč乊čĆą╝ąĖčĆąŠą▓ą░ąĮąĖčÅ ąĘą░ą╝ąŠčĆąŠąČąĄąĮąĮčŗčģ ą┐ąŠčĆąŠą┤ ą┤ąŠą╗ąČąĄąĮ ą┐čĆąŠą▓ąŠą┤ąĖčéčīčüčÅ ąĮą░ ą▒ą░ąĘąĄ ą┤čĆčāą│ąĖčģ ą║čĆąĖč鹥čĆąĖąĄą▓ ŌĆō ą£ąŠčĆą░ ŌĆō ąÜčāą╗ąŠąĮą░ [12-14] ąĖ ąöčĆčāą║ąĄčĆą░ ŌĆō ą¤čĆą░ą│ąĄčĆą░ [15] ąĖą╗ąĖ ąĖčģ ą╝ąŠą┤ąĖčäąĖą║ą░čåąĖą╣ [16, 17]. ą¤ą░čĆą░ą╝ąĄčéčĆą░ą╝ąĖ čŹčéąĖčģ ą║čĆąĖč鹥čĆąĖąĄą▓ čÅą▓ą╗čÅčÄčéčüčÅ ą┐čĆąŠčćąĮąŠčüčéąĮčŗąĄ čüą▓ąŠą╣čüčéą▓ą░ ąĘą░ą╝ąŠčĆąŠąČąĄąĮąĮčŗčģ ą┐ąŠčĆąŠą┤ ŌĆō čüčåąĄą┐ą╗ąĄąĮąĖąĄ C ąĖ čāą│ąŠą╗ ą▓ąĮčāčéčĆąĄąĮąĮąĄą│ąŠ čéčĆąĄąĮąĖčÅ Žå [18]. ą¤čĆąĖ čŹč鹊ą╝ ą▓ą░ąČąĮąŠ ą┐ąŠąĮąĖą╝ą░čéčī, čćč鹊 ą┐čĆąĖ ąĘą░ą╝ąŠčĆą░ąČąĖą▓ą░ąĮąĖąĖ ą┐ąŠčĆąŠą┤ ąĮą░ ą▒ąŠą╗čīčłąĖčģ ą│ą╗čāą▒ąĖąĮą░čģ ą┐čĆąĖ ą▓čŗčüąŠą║ąŠą╝ ą▓čüąĄčüč鹊čĆąŠąĮąĮąĄą╝ čüąČąĖą╝ą░čÄčēąĄą╝ ą┤ą░ą▓ą╗ąĄąĮąĖąĖ ą║čĆąĖč鹥čĆąĖąĖ ą£ąŠčĆą░ ŌĆō ąÜčāą╗ąŠąĮą░ ąĖ ąöčĆčāą║ąĄčĆą░ ŌĆō ą¤čĆą░ą│ąĄčĆą░ čéą░ą║ąČąĄ čüčéą░ąĮąŠą▓čÅčéčüčÅ ąĮąĄą┐čĆąĖą╝ąĄąĮąĖą╝čŗ ąĖ čéčĆąĄą▒čāčÄčé ą╝ąŠą┤ąĖčäąĖą║ą░čåąĖą╣ [19].
ą¤čĆąŠčćąĮąŠčüčéąĮčŗąĄ čüą▓ąŠą╣čüčéą▓ą░ ąĪ ąĖ j ą▓ąŠčłą╗ąĖ ą▓ ą║ą░č湥čüčéą▓ąĄ ąĖčüčģąŠą┤ąĮčŗčģ ą┤ą░ąĮąĮčŗčģ ą▓ ąĖąĘą▓ąĄčüčéąĮčāčÄ č乊čĆą╝čāą╗čā ąĪ.ąĪ.ąÆčÅą╗ąŠą▓ą░ ą┤ą╗čÅ ąŠą┐čĆąĄą┤ąĄą╗ąĄąĮąĖčÅ čéčĆąĄą▒čāąĄą╝ąŠą╣ ą┐ąŠ čāčüą╗ąŠą▓ąĖčÄ ą┐čĆąŠčćąĮąŠčüčéąĖ č鹊ą╗čēąĖąĮčŗ ąøą¤ą× [20, 21]:
ą│ą┤ąĄ R ŌĆō čĆą░ą┤ąĖčāčü ą▓ąĮčāčéčĆąĄąĮąĮąĄą╣ ą│čĆą░ąĮąĖčåčŗ ąøą¤ą×, ą╝; P ŌĆō ą▓ąĮąĄčłąĮčÅčÅ ąĮą░ą│čĆčāąĘą║ą░, ą¤ą░.
ążąŠčĆą╝čāą╗ą░ (1) ąĮąĄ ąĘą░ą║čĆąĄą┐ą╗ąĄąĮą░ ą▓ ąĮąŠčĆą╝ą░čéąĖą▓ąĮąŠą╣ ą╗ąĖč鹥čĆą░čéčāčĆąĄ, ąĮąŠ čćą░čüč鹊 ąĖčüą┐ąŠą╗čīąĘčāąĄčéčüčÅ ą┐čĆąĖ ą░ąĮą░ą╗ąĖąĘąĄ č鹊ą╗čēąĖąĮčŗ ąøą¤ą× ą┐ąŠ čāčüą╗ąŠą▓ąĖčÄ ą┐čĆąŠčćąĮąŠčüčéąĖ. ą×ąĮą░ čüąŠąŠčéą▓ąĄčéčüčéą▓čāąĄčé čüą╗čāčćą░čÄ ąĮąĄą┐ąŠą┤ą║čĆąĄą┐ą╗ąĄąĮąĮąŠą│ąŠ ą╗ąĄą┤ąŠą┐ąŠčĆąŠą┤ąĮąŠą│ąŠ čåąĖą╗ąĖąĮą┤čĆą░ ąĮąĄąŠą│čĆą░ąĮąĖč湥ąĮąĮąŠą╣ ą▓čŗčüąŠčéčŗ ąĘą░čģąŠą┤ą║ąĖ h. ąöą╗čÅ čüą╗čāčćą░čÅ ą║ąŠąĮąĄčćąĮąŠą╣ ą▓čŗčüąŠčéčŗ ąĘą░čģąŠą┤ą║ąĖ ąĪ.ąĪ.ąÆčÅą╗ąŠą▓čŗą╝ čéą░ą║ąČąĄ ą▓čŗą▓ąĄą┤ąĄąĮą░ čĆą░čüč湥čéąĮą░čÅ č乊čĆą╝čāą╗ą░:
ą│ą┤ąĄ ŽāčüąČ ŌĆō ą┐čĆąĄą┤ąĄą╗ ą┐čĆąŠčćąĮąŠčüčéąĖ ąĮą░ ąŠą┤ąĮąŠąŠčüąĮąŠąĄ čüąČą░čéąĖąĄ ą┤ą╗čÅ ąĘą░ą╝ąŠčĆąŠąČąĄąĮąĮąŠą╣ ą┐ąŠčĆąŠą┤čŗ, ą£ą¤ą░.
ą×ą┤ąĮą░ą║ąŠ ą┐čĆąĖ ą▓čŗą▓ąŠą┤ąĄ č乊čĆą╝čāą╗čŗ (2) ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ą╗ąĖčüčī ą┤čĆčāą│ąĖąĄ, ą▒ąŠą╗ąĄąĄ ą│čĆčāą▒čŗąĄ čāą┐čĆąŠčēąĄąĮąĖčÅ, čćč鹊 ą┐čĆąĖą▓ąŠą┤ąĖą╗ąŠ ą║ čüčāčēąĄčüčéą▓ąĄąĮąĮąŠ ąĘą░ą▓čŗčłąĄąĮąĮčŗą╝ ą▓ąĄą╗ąĖčćąĖąĮą░ą╝ č鹊ą╗čēąĖąĮ ąøą¤ą× ą▓ čüą╗čāčćą░ąĄ čĆą░čüčüą╝ąŠčéčĆąĄąĮąĖčÅ čĆąĄą░ą╗čīąĮąŠą│ąŠ ą┤ąĖą░ą┐ą░ąĘąŠąĮą░ ąĘąĮą░č湥ąĮąĖą╣ ą▓čŗčüąŠčé ąĘą░čģąŠą┤ą║ąĖ (3-12 ą╝).
ąóą░ą║ąČąĄ čćą░čüč鹊 ą┐čĆąĖ ą░ąĮą░ą╗ąĖąĘąĄ ąĮąĄą╗ąĖąĮąĄą╣ąĮąŠą│ąŠ ą┤ąĄč乊čĆą╝ąĖčĆąŠą▓ą░ąĮąĖčÅ ąĘą░ą╝ąŠčĆąŠąČąĄąĮąĮčŗčģ ą┐ąŠčĆąŠą┤ ąĖčüčüą╗ąĄą┤ąŠą▓ą░č鹥ą╗ąĖ ąĖčüą┐ąŠą╗čīąĘčāčÄčé ą▒ąŠą╗ąĄąĄ čüą╗ąŠąČąĮčŗąĄ čĆąĄąŠą╗ąŠą│ąĖč湥čüą║ąĖąĄ ą╝ąŠą┤ąĄą╗ąĖ, ąĮą░ą┐čĆąĖą╝ąĄčĆ ą╝ąŠą┤ąĄą╗čī ąØąĖčłąĖčģą░čĆčŗ [21, 22], ą╝ąŠą┤ąĄą╗čī Barcelona [23] ąĖ ą┤čĆ. ąæąŠą╗ąĄąĄ čüą╗ąŠąČąĮčŗąĄ ą╝ąŠą┤ąĄą╗ąĖ čāč湥čéą░ ąĮąĄčāą┐čĆčāą│ąŠą│ąŠ ą┐ąŠą▓ąĄą┤ąĄąĮąĖčÅ ąĘą░ą╝ąŠčĆąŠąČąĄąĮąĮčŗčģ ą┐ąŠčĆąŠą┤ čéčĆąĄą▒čāčÄčé ą▒ąŠą╗čīčłąĄą│ąŠ ą║ąŠą╗ąĖč湥čüčéą▓ą░ ą┐ą░čĆą░ą╝ąĄčéčĆąŠą▓, ąŠą┐čĆąĄą┤ąĄą╗ąĄąĮąĖąĄ ą║ąŠč鹊čĆčŗčģ ą▓ čĆą░ą╝ą║ą░čģ ą╗ą░ą▒ąŠčĆą░č鹊čĆąĮčŗčģ ąĖčüą┐čŗčéą░ąĮąĖą╣ ą╝ąŠąČąĄčé ąŠą║ą░ąĘą░čéčīčüčÅ ąĮąĄčéčĆąĖą▓ąĖą░ą╗čīąĮčŗą╝, ą░ ąĖčģ ą┐čĆąĖą╝ąĄąĮąĄąĮąĖąĄ ą▓ čĆąĄčłąĄąĮąĖąĖ ą┐čĆąĖą║ą╗ą░ą┤ąĮčŗčģ ąĘą░ą┤ą░čć ą┐čĆąŠą│ąĮąŠąĘą░ ąĮą░ą┐čĆčÅąČąĄąĮąĮąŠ-ą┤ąĄč乊čĆą╝ąĖčĆąŠą▓ą░ąĮąĮąŠą│ąŠ čüąŠčüč鹊čÅąĮąĖčÅ ą┐ąŠčĆąŠą┤ąĮąŠą│ąŠ ą╝ą░čüčüąĖą▓ą░ ą┐čĆąĖ čüčéčĆąŠąĖč鹥ą╗čīčüčéą▓ąĄ čłą░čģčéąĮąŠą│ąŠ čüčéą▓ąŠą╗ą░ ŌĆō ąĮąĄą▓ąŠąĘą╝ąŠąČąĮčŗą╝.
ą×čéąĮąŠčüąĖč鹥ą╗čīąĮąŠ ą┐čĆąŠčüčéčŗąĄ ą╝ąŠą┤ąĄą╗ąĖ ąĮąĄą╗ąĖąĮąĄą╣ąĮąŠą│ąŠ ą┤ąĄč乊čĆą╝ąĖčĆąŠą▓ą░ąĮąĖčÅ ąĘą░ą╝ąŠčĆą░ąČąĖą▓ą░ąĄą╝čŗčģ ą▓čÅąĘą║ąŠčāą┐čĆčāą│ąŠą┐ą╗ą░čüčéąĖčćąĮčŗčģ čüčĆąĄą┤ ą┐čĆąĖą╝ąĄąĮčÅčÄčéčüčÅ ą▓ čĆą░čüč湥č鹥 č鹊ą╗čēąĖąĮčŗ ąøą¤ą× ą┐ąŠ čāčüą╗ąŠą▓ąĖčÄ ą┐ąŠą╗ąĘčāč湥čüčéąĖ, ą║ąŠč鹊čĆąŠąĄ ą┤ą╗čÅ ąĮąĄą║ąŠč鹊čĆčŗčģ čéąĖą┐ąŠą▓ ą│čĆčāąĮč鹊ą▓ ąĖ ą┐ąŠčĆąŠą┤ čÅą▓ą╗čÅąĄčéčüčÅ ąĮąĄ ą╝ąĄąĮąĄąĄ ą▓ą░ąČąĮčŗą╝, č湥ą╝ čāčüą╗ąŠą▓ąĖąĄ ą┐čĆąŠčćąĮąŠčüčéąĖ [24-26]. ąĀą░čüč湥čé ą┐ąŠ čāčüą╗ąŠą▓ąĖčÄ ą┐ąŠą╗ąĘčāč湥čüčéąĖ ąĘą░ą║ą╗čÄčćą░ąĄčéčüčÅ ą▓ ąŠą┐čĆąĄą┤ąĄą╗ąĄąĮąĖąĖ čéą░ą║ąŠą╣ č鹊ą╗čēąĖąĮčŗ ąøą¤ą×, ą┐čĆąĖ ą║ąŠč鹊čĆąŠą╣ ą╝ą░ą║čüąĖą╝ą░ą╗čīąĮąŠąĄ čĆą░ą┤ąĖą░ą╗čīąĮąŠąĄ čüą╝ąĄčēąĄąĮąĖąĄ ąĄą│ąŠ ą▓ąĮčāčéčĆąĄąĮąĮąĄą╣ čüč鹥ąĮą║ąĖ ą┐ąŠą┤ ą┤ąĄą╣čüčéą▓ąĖąĄą╝ ąĮą░ą│čĆčāąĘą║ąĖ ąĮą░ ą▓ąĮąĄčłąĮčÄčÄ ąĮąĄ ą┐čĆąĄą▓čŗčüąĖčé ą┐čĆąĄą┤ąĄą╗čīąĮąŠą╣ ą┤ąŠą┐čāčüčéąĖą╝ąŠą╣ ą▓ąĄą╗ąĖčćąĖąĮčŗ ╬ö ąĘą░ ąĘą░ą┤ą░ąĮąĮąŠąĄ ą▓čĆąĄą╝čÅ tp. ąÆąĄą╗ąĖčćąĖąĮą░ ╬ö ąŠą┐čĆąĄą┤ąĄą╗čÅąĄčéčüčÅ, ąĖčüčģąŠą┤čÅ ąĖąĘ č鹥čģąĮąŠą╗ąŠą│ąĖąĖ ą┐čĆąŠčģąŠą┤ą║ąĖ čüčéą▓ąŠą╗ą░ ąĖą╗ąĖ ąĖąĘ ą┤ąŠą┐čāčüčéąĖą╝ąŠą╣ ą▓ąĄą╗ąĖčćąĖąĮčŗ ą┐čĆąŠą│ąĖą▒ą░ ąĘą░ą╝ąŠčĆą░ąČąĖą▓ą░čÄčēąĖčģ ą║ąŠą╗ąŠąĮąŠą║ [8, 27]. ąÆ ą┤ą░ąĮąĮąŠą╣ čüčéą░čéčīąĄ čĆą░čüčüą╝ą░čéčĆąĖą▓ą░ąĄčéčüčÅ čĆą░čüč湥čé č鹊ą╗čēąĖąĮčŗ ąøą¤ą× ąĖą╝ąĄąĮąĮąŠ ą┐ąŠ čāčüą╗ąŠą▓ąĖčÄ ą┐čĆąŠčćąĮąŠčüčéąĖ (ąĖą╗ąĖ ą┐ąŠ ą┐čĆąĄą┤ąĄą╗čīąĮąŠą╝čā ąĮą░ą┐čĆčÅąČąĄąĮąĮąŠą╝čā čüąŠčüč鹊čÅąĮąĖčÄ).
ążąŠčĆą╝čāą╗ą░ (1) ą┤ą╗čÅ čĆą░čüč湥čéą░ ąøą¤ą× ą┐ąŠ čāčüą╗ąŠą▓ąĖčÄ ą┐čĆąŠčćąĮąŠčüčéąĖ ąĮąĄ čāčćąĖčéčŗą▓ą░ąĄčé čĆčÅą┤ ąĘąĮą░čćąĖą╝čŗčģ čäąĖąĘąĖč湥čüą║ąĖčģ čäą░ą║č鹊čĆąŠą▓:
- ą║ąŠąĮąĄčćąĮčāčÄ ą▓čŗčüąŠčéčā ąĘą░čģąŠą┤ą║ąĖ;
- čćą░čüčéąĖčćąĮąŠąĄ ą▓ąŠčüą┐čĆąĖčÅčéąĖąĄ ą┤ą░ą▓ą╗ąĄąĮąĖčÅ ą▒ąŠą║ąŠą▓ąŠą│ąŠ čĆą░čüą┐ąŠčĆą░ ąŠą║čĆčāąČą░čÄčēąĖą╝ąĖ ą│ąŠčĆąĮčŗą╝ąĖ ą┐ąŠčĆąŠą┤ą░ą╝ąĖ;
- ąĮą░čćą░ą╗čīąĮąŠąĄ ą┤ąĄč乊čĆą╝ąĖčĆąŠą▓ą░ąĮąĮąŠąĄ čüąŠčüč鹊čÅąĮąĖąĄ ą┐ąŠčĆąŠą┤ ąĘą░ čüč湥čé č鹥ą┐ą╗ąŠą▓ąŠą╣ ą┤ąĄč乊čĆą╝ą░čåąĖąĖ čéą▓ąĄčĆą┤čŗčģ čćą░čüčéąĖčå ą┐ąŠčĆąŠą┤čŗ ąĖ čĆą░čüčłąĖčĆąĄąĮąĖčÅ ą▓ąŠą┤čŗ ą┐čĆąĖ ąĘą░ą╝ąĄčƹʹ░ąĮąĖąĖ ą▓ ą┐ąŠčĆą░čģ;
- ąĮąĄąŠą┤ąĮąŠčĆąŠą┤ąĮąŠąĄ ą┐ąŠą╗ąĄ č鹥ą╝ą┐ąĄčĆą░čéčāčĆ ą▓ ąŠą▒čŖąĄą╝ąĄ ąĘą░ą╝ąŠčĆąŠąČąĄąĮąĮčŗčģ ą┐ąŠčĆąŠą┤;
- ą▓ąĄčĆčéąĖą║ą░ą╗čīąĮčāčÄ ąĮą░ą│čĆčāąĘą║čā.
ąÆ čĆą░ą▒ąŠčéą░čģ [13, 14, 28] ą▒čŗą╗ąĖ ą┐čĆąĄą┤ą┐čĆąĖąĮčÅčéčŗ ą┐ąŠą┐čŗčéą║ąĖ ą╝ąŠą┤ąĖčäąĖą║ą░čåąĖąĖ č乊čĆą╝čāą╗čŗ (1) čü čāč湥č鹊ą╝ čäą░ą║č鹊čĆąŠą▓ 2, 3 ąĖ 4. ążą░ą║č鹊čĆčŗ 1 ąĖ 5 ąĮą░ ąĮą░ą┐čĆčÅąČąĄąĮąĮąŠ-ą┤ąĄč乊čĆą╝ąĖčĆąŠą▓ą░ąĮąĮąŠąĄ čüąŠčüč鹊čÅąĮąĖąĄ (ąØąöąĪ) ąĘą░ą╝ąŠčĆą░ąČąĖą▓ą░ąĄą╝čŗčģ ą┐ąŠčĆąŠą┤ čéą░ą║ąČąĄ čāčćąĖčéčŗą▓ą░ą╗ąĖčüčī, ąĮąŠ ą▓ čĆą░ą╝ą║ą░čģ ą┤čĆčāą│ąŠą╣ ą╝ąĄč鹊ą┤ąŠą╗ąŠą│ąĖąĖ ŌĆō čćąĖčüą╗ąĄąĮąĮąŠą│ąŠ ą╝ąŠą┤ąĄą╗ąĖčĆąŠą▓ą░ąĮąĖčÅ čüąŠą┐čĆčÅąČąĄąĮąĮčŗčģ č鹥čĆą╝ąŠą│ąĖą┤čĆąŠą╝ąĄčģą░ąĮąĖč湥čüą║ąĖčģ ą┐čĆąŠčåąĄčüčüąŠą▓ [23, 29, 30]. ą×ą┤ąĮą░ą║ąŠ ąĮąĄ čāą┤ą░ą╗ąŠčüčī ą┐ąŠą╗čāčćąĖčéčī čāąĮąĖą▓ąĄčĆčüą░ą╗čīąĮčāčÄ č乊čĆą╝čāą╗čā ąŠą┐čĆąĄą┤ąĄą╗ąĄąĮąĖčÅ čéčĆąĄą▒čāąĄą╝ąŠą╣ č鹊ą╗čēąĖąĮčŗ ąøą¤ą× ą┤ą╗čÅ ą┐čĆąŠąĖąĘą▓ąŠą╗čīąĮąŠą│ąŠ čüą╗čāčćą░čÅ.
ąÆ čüčéą░čéčīąĄ ąŠą┐ąĖčüą░ąĮą░ ą▓ąŠąĘą╝ąŠąČąĮąŠčüčéčī ą┐ąŠčüčéčĆąŠąĄąĮąĖčÅ ą░ąĮą░ą╗ąĖčéąĖč湥čüą║ąŠą╣ čĆą░čüč湥čéąĮąŠą╣ č乊čĆą╝čāą╗čŗ ąŠą┐čĆąĄą┤ąĄą╗ąĄąĮąĖčÅ č鹊ą╗čēąĖąĮčŗ ąøą¤ą× ąĖąĘ čāčüą╗ąŠą▓ąĖčÅ ą┐čĆąĄą┤ąĄą╗čīąĮąŠą│ąŠ ąĮą░ą┐čĆčÅąČąĄąĮąĮąŠą│ąŠ čüąŠčüč鹊čÅąĮąĖčÅ čü čāč湥č鹊ą╝ ą║ąŠąĮąĄčćąĮąŠą╣ ą▓čŗčüąŠčéčŗ ąĘą░čģąŠą┤ą║ąĖ ąĖ ą┐čĆąĄą┤ą╗ąŠąČąĄąĮą░ ą╝ąŠą┤ąĖčäąĖą║ą░čåąĖčÅ č乊čĆą╝čāą╗čŗ (1), ą▓ą║ą╗čÄčćą░čÄčēą░čÅ ą▓ čüąĄą▒čÅ ąĮąŠą▓čŗą╣ ą┐ą░čĆą░ą╝ąĄčéčĆ ŌĆō ą▓čŗčüąŠčéčā ąĘą░čģąŠą┤ą║ąĖ.
ą£ąĄč鹊ą┤ąŠą╗ąŠą│ąĖčÅ
ąĪą╗čāčćą░ą╣ ąĮąĄąŠą│čĆą░ąĮąĖč湥ąĮąĮąŠą╣ ą▓čŗčüąŠčéčŗ ąĘą░čģąŠą┤ą║ąĖ
ąÆ ąĖčüčüą╗ąĄą┤ąŠą▓ą░ąĮąĖąĖ čāą┐čĆčāą│ąŠą┐ą╗ą░čüčéąĖč湥čüą║ąŠąĄ ą┤ąĄč乊čĆą╝ąĖčĆąŠą▓ą░ąĮąĖąĄ ąĘą░ą╝ąŠčĆąŠąČąĄąĮąĮčŗčģ ą┐ąŠčĆąŠą┤ ą░ąĮą░ą╗ąĖąĘąĖčĆąŠą▓ą░ą╗ąŠčüčī ą▓ ą┐čĆąŠčüč鹊ą╣ ą╝ą░č鹥ą╝ą░čéąĖč湥čüą║ąŠą╣ ą┐ąŠčüčéą░ąĮąŠą▓ą║ąĄ. ąöąŠ ą┤ą▓čāčģą╝ąĄčĆąĮąŠą╣ ą┐ąŠčüčéą░ąĮąŠą▓ą║ąĖ ąĘą░ą┤ą░čćąĖ čü ą║ąŠąĮąĄčćąĮąŠą╣ ą▓čŗčüąŠč鹊ą╣ ąĘą░čģąŠą┤ą║ąĖ čĆą░čüčüą╝ą░čéčĆąĖą▓ą░ąĄčéčüčÅ ą▒ąŠą╗ąĄąĄ ą┐čĆąŠčüčéą░čÅ ąŠą┤ąĮąŠą╝ąĄčĆąĮą░čÅ čüąĖčéčāą░čåąĖčÅ ą┐ąŠą╗ąŠą│ąŠ čåąĖą╗ąĖąĮą┤čĆą░ ąĖąĘ ąĘą░ą╝ąŠčĆąŠąČąĄąĮąĮčŗčģ ą┐ąŠčĆąŠą┤, ąĖą╝ąĄčÄčēąĄą│ąŠ ąĮąĄąŠą│čĆą░ąĮąĖč湥ąĮąĮąŠ ą▒ąŠą╗čīčłčāčÄ ą▓čŗčüąŠčéčā ąĘą░čģąŠą┤ą║ąĖ, ą▓ąĮčāčéčĆąĄąĮąĮąĖą╣ ąĖ ą▓ąĮąĄčłąĮąĖą╣ čĆą░ą┤ąĖčāčüčŗ a ąĖ b čüąŠąŠčéą▓ąĄčéčüčéą▓ąĄąĮąĮąŠ (čĆąĖčü.1). ąóą░ą║ą░čÅ ą┐ąŠčüčéą░ąĮąŠą▓ą║ą░ ą▒čŗą╗ą░ čĆą░čüčüą╝ąŠčéčĆąĄąĮą░ ą▓ ąĖčüč鹊čćąĮąĖą║ąĄ [3].
ąØą░ ą▓ąĮąĄčłąĮąĄą╣ ą│čĆą░ąĮąĖčåąĄ čĆą░čüč湥čéąĮąŠą╣ ąŠą▒ą╗ą░čüčéąĖ ą┐čĆąĖą║ą╗ą░ą┤čŗą▓ą░ąĄčéčüčÅ ąĘą░ą┤ą░ąĮąĮą░čÅ čĆą░ą▓ąĮąŠą╝ąĄčĆąĮą░čÅ ąĮą░ą│čĆčāąĘą║ą░, ą░ ąĮą░ ą▓ąĮčāčéčĆąĄąĮąĮąĄą╣ ąĘą░ą┤ą░ąĄčéčüčÅ čüą▓ąŠą▒ąŠą┤ąĮą░čÅ ąĮąĄąĮą░ą│čĆčāąČąĄąĮąĮą░čÅ ą┐ąŠą▓ąĄčĆčģąĮąŠčüčéčī. ą¤čĆąĄą┤ą┐ąŠą╗ą░ą│ą░ąĄčéčüčÅ, čćč鹊 ą│ąŠčĆąĮą░čÅ ą┐ąŠčĆąŠą┤ą░ ą┐čĆąĄą┤čüčéą░ą▓ą╗čÅąĄčé čüąŠą▒ąŠą╣ ąŠą┤ąĮąŠčĆąŠą┤ąĮčŗą╣ ąĖ ąĖąĘąŠčéčĆąŠą┐ąĮčŗą╣ ą╝ą░č鹥čĆąĖą░ą╗, ą░ ąØąöąĪ čÅą▓ą╗čÅąĄčéčüčÅ ą┐ą╗ąŠčüą║ąŠą┤ąĄč乊čĆą╝ąĖčĆąŠą▓ą░ąĮąĮčŗą╝. ąóą░ą║ąĖą╝ ąŠą▒čĆą░ąĘąŠą╝, ąĖą╝ąĄąĄčé ą╝ąĄčüč鹊 ą▓čĆą░čēą░č鹥ą╗čīąĮą░čÅ čüąĖą╝ą╝ąĄčéčĆąĖčÅ ą▓ ą│ąĄąŠą╝ąĄčéčĆąĖąĖ, čüą▓ąŠą╣čüčéą▓ą░čģ ą┐ąŠčĆąŠą┤ ąĖ ą│čĆą░ąĮąĖčćąĮčŗčģ čāčüą╗ąŠą▓ąĖčÅčģ ąĘą░ą┤ą░čćąĖ, ą░ ą┐ąŠč鹊ą╝čā čāą╝ąĄčüčéąĮąŠ ą┐čĆąĄą┤ą┐ąŠą╗ąŠąČąĖčéčī, čćč鹊 čĆąĄčłąĄąĮąĖąĄ ąĘą░ą┤ą░čćąĖ ą▓ čåąĄą╗ąŠą╝ čéą░ą║ąČąĄ ąŠą▒ą╗ą░ą┤ą░ąĄčé ą┤ą░ąĮąĮčŗą╝ ą▓ąĖą┤ąŠą╝ čüąĖą╝ą╝ąĄčéčĆąĖąĖ. ąÆ čéą░ą║ąŠą╝ čüą╗čāčćą░ąĄ č鹊ą╗čīą║ąŠ čĆą░ą┤ąĖą░ą╗čīąĮčŗąĄ ą┐ąĄčĆąĄą╝ąĄčēąĄąĮąĖčÅ ąŠą║ą░ąČčāčéčüčÅ ąĮąĄ čĆą░ą▓ąĮčŗą╝ąĖ ąĮčāą╗čÄ. ą£ą░č鹥ą╝ą░čéąĖč湥čüą║ą░čÅ ą┐ąŠčüčéą░ąĮąŠą▓ą║ą░ ąĘą░ą┤ą░čćąĖ:
- čāčĆą░ą▓ąĮąĄąĮąĖąĄ čĆą░ą▓ąĮąŠą▓ąĄčüąĖčÅ
- ąĘąŠąĮą░ čāą┐čĆčāą│ąŠą│ąŠ ą┤ąĄč乊čĆą╝ąĖčĆąŠą▓ą░ąĮąĖčÅ
- ąĘąŠąĮą░ ą┐ą╗ą░čüčéąĖč湥čüą║ąŠą│ąŠ č鹥č湥ąĮąĖčÅ, ąŠą┐čĆąĄą┤ąĄą╗čÅąĄą╝ą░čÅ ą║čĆąĖč鹥čĆąĖąĄą╝ ą£ąŠčĆą░ ŌĆō ąÜčāą╗ąŠąĮą░
- ą│čĆą░ąĮąĖčćąĮčŗąĄ čāčüą╗ąŠą▓ąĖčÅ
ą│ą┤ąĄ Žār ąĖ Žā╬Ė ŌĆō čĆą░ą┤ąĖą░ą╗čīąĮą░čÅ ąĖ čāą│ą╗ąŠą▓ą░čÅ (čéą░ąĮą│ąĄąĮčåąĖą░ą╗čīąĮą░čÅ) ą║ąŠą╝ą┐ąŠąĮąĄąĮčéčŗ č鹥ąĮąĘąŠčĆą░ ąĮą░ą┐čĆčÅąČąĄąĮąĖą╣ čüąŠąŠčéą▓ąĄčéčüčéą▓ąĄąĮąĮąŠ, ą¤ą░; K ŌĆō ąŠą▒čŖąĄą╝ąĮčŗą╣ ą╝ąŠą┤čāą╗čī čāą┐čĆčāą│ąŠčüčéąĖ, ą¤ą░; G ŌĆō ą╝ąŠą┤čāą╗čī čüą┤ą▓ąĖą│ą░, ą¤ą░; ╬Ąr, ╬Ą╬Ė ŌĆō čĆą░ą┤ąĖą░ą╗čīąĮą░čÅ ąĖ čéą░ąĮą│ąĄąĮčåąĖą░ą╗čīąĮą░čÅ ą║ąŠą╝ą┐ąŠąĮąĄąĮčéčŗ č鹥ąĮąĘąŠčĆą░ ą┤ąĄč乊čĆą╝ą░čåąĖą╣ čüąŠąŠčéą▓ąĄčéčüčéą▓ąĄąĮąĮąŠ; u ŌĆō čĆą░ą┤ąĖą░ą╗čīąĮąŠąĄ ą┐ąĄčĆąĄą╝ąĄčēąĄąĮąĖąĄ, ą╝; ╬Š ŌĆō ą│čĆą░ąĮąĖčåą░ ą╝ąĄąČą┤čā čāą┐čĆčāą│ąŠą╣ ąĘąŠąĮąŠą╣ ąĖ ąĘąŠąĮąŠą╣ ą┐ą╗ą░čüčéąĖč湥čüą║ąŠą│ąŠ č鹥č湥ąĮąĖčÅ, ą╝.
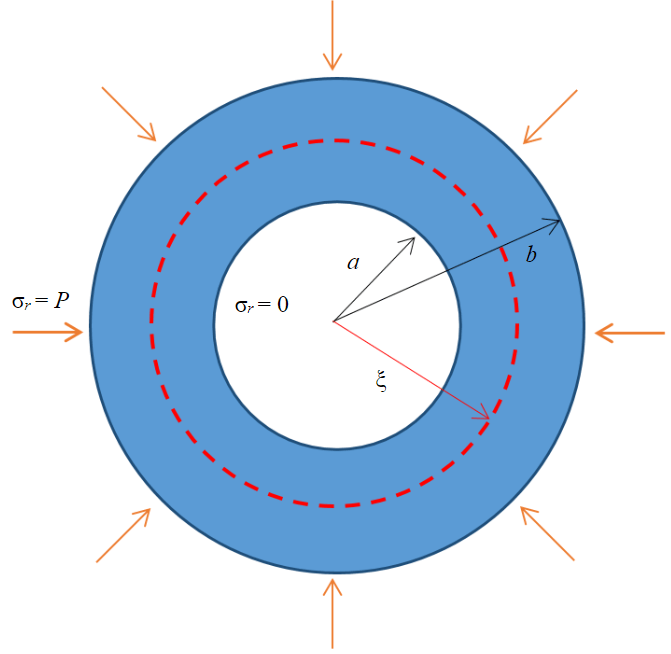
ąĀąĖčü.1. ąōąĄąŠą╝ąĄčéčĆąĖčÅ čĆą░čüč湥čéąĮąŠą╣ ąŠą▒ą╗ą░čüčéąĖ ą┐čĆąĖ čĆą░čüčüą╝ąŠčéčĆąĄąĮąĖąĖ ąĮąĄąŠą│čĆą░ąĮąĖč湥ąĮąĮąŠą╣ ą▓čŗčüąŠčéčŗ ąĘą░čģąŠą┤ą║ąĖ
ą¤čĆąĖąĮčÅč鹊, čćč鹊 čüąČąĖą╝ą░čÄčēąĖąĄ ąĮą░ą┐čĆčÅąČąĄąĮąĖčÅ ąĖą╝ąĄčÄčé ą┐ąŠą╗ąŠąČąĖč鹥ą╗čīąĮčŗą╣ ąĘąĮą░ą║, ą░ čĆą░čüčéčÅą│ąĖą▓ą░čÄčēąĖąĄ ŌĆō ąŠčéčĆąĖčåą░č鹥ą╗čīąĮčŗą╣ [31]. ąÆ ą║ą░č湥čüčéą▓ąĄ ą│čĆą░ąĮąĖčćąĮčŗčģ čāčüą╗ąŠą▓ąĖą╣ ą╝ąĄąČą┤čā ą┤ą▓čāą╝čÅ ąĘąŠąĮą░ą╝ąĖ ą▓čŗą▒čĆą░ąĮčŗ ą┤ą▓ą░ čāčüą╗ąŠą▓ąĖčÅ ą┐ąŠ ąĮą░ą┐čĆčÅąČąĄąĮąĖčÅą╝, ąĮąŠ ąŠčéčüčāčéčüčéą▓čāąĄčé čāčüą╗ąŠą▓ąĖąĄ ąĮąĄčĆą░ąĘčĆčŗą▓ąĮąŠčüčéąĖ ą┐ąŠ ą┐ąĄčĆąĄą╝ąĄčēąĄąĮąĖčÅą╝. ąóąĄą╝ ąĮąĄ ą╝ąĄąĮąĄąĄ, ąŠąĮąŠ ą▓čŗą┐ąŠą╗ąĮčÅąĄčéčüčÅ ą░ą▓č鹊ą╝ą░čéąĖč湥čüą║ąĖ ą┐čĆąĖ ą▓čŗą┐ąŠą╗ąĮąĄąĮąĖąĖ čĆą░ą▓ąĄąĮčüčéą▓ (10). ąÆąĄą╗ąĖčćąĖąĮą░ ╬Š čÅą▓ą╗čÅąĄčéčüčÅ ąĖčüą║ąŠą╝čŗą╝ ą┐ą░čĆą░ą╝ąĄčéčĆąŠą╝ ąĮą░čĆčÅą┤čā čü čäčāąĮą║čåąĖčÅą╝ąĖ Žār, Žā╬Ė ąĖ ą┤čĆ.
ąÜą░ą║ čāą║ą░ąĘą░ąĮąŠ ą▓ ąĖčüč鹊čćąĮąĖą║ąĄ [27], ąĘą░čĆąŠąČą┤ąĄąĮąĖąĄ ąĖ čĆą░ąĘą▓ąĖčéąĖąĄ ąĘąŠąĮčŗ čāą┐čĆčāą│ąŠą┐ą╗ą░čüčéąĖč湥čüą║ąŠą│ąŠ ą┤ąĄč乊čĆą╝ąĖčĆąŠą▓ą░ąĮąĖčÅ ą┐čĆąŠąĖčüčģąŠą┤ąĖčé čü ą▓ąĮčāčéčĆąĄąĮąĮąĄą╣ ą│čĆą░ąĮąĖčåčŗ ąøą¤ą×. ąĪčćąĖčéą░ąĄčéčüčÅ, čćč鹊 ąøą¤ą× č鹥čĆčÅąĄčé čüą▓ąŠčÄ ąĮąĄčüčāčēčāčÄ čüą┐ąŠčüąŠą▒ąĮąŠčüčéčī, ą║ąŠą│ą┤ą░ ąĘąŠąĮą░ ą┐ą╗ą░čüčéąĖč湥čüą║ąŠą│ąŠ č鹥č湥ąĮąĖčÅ čĆą░čüą┐čĆąŠčüčéčĆą░ąĮčÅąĄčéčüčÅ ąĮą░ ą▓čüčÄ č鹊ą╗čēąĖąĮčā ąøą¤ą× ąĖ ą▓ą┐ąĄčĆą▓čŗąĄ ą║ą░čüą░ąĄčéčüčÅ ąĄą│ąŠ ą▓ąĮąĄčłąĮąĄą╣ ą│čĆą░ąĮąĖčåčŗ. ąśą╝ąĄąĮąĮąŠ ą┤ą╗čÅ čŹč鹊ą│ąŠ čüąŠčüč鹊čÅąĮąĖčÅ ą┐čĆąĄą┤ąĄą╗čīąĮąŠą│ąŠ čĆą░ą▓ąĮąŠą▓ąĄčüąĖčÅ ąŠą┐čĆąĄą┤ąĄą╗čÅąĄčéčüčÅ čĆą░čüč湥čéąĮą░čÅ č鹊ą╗čēąĖąĮą░ ąøą¤ą×.
ąĀą░ąĮąĄąĄ čĆąĄčłąĄąĮąĖąĄ čüąĖčüč鹥ą╝čŗ čāčĆą░ą▓ąĮąĄąĮąĖą╣ (5)-(10) ąĖčüčüą╗ąĄą┤ąŠą▓ą░ą╗ąŠčüčī č鹊ą╗čīą║ąŠ čćą░čüčéąĖčćąĮąŠ, ą▓ č鹥čĆą╝ąĖąĮą░čģ ąĮą░ą┐čĆčÅąČąĄąĮąĖą╣, č湥ą│ąŠ ą▒čŗą╗ąŠ ą┤ąŠčüčéą░č鹊čćąĮąŠ ą┤ą╗čÅ ąŠą┐čĆąĄą┤ąĄą╗ąĄąĮąĖčÅ ą┐čĆąĄą┤ąĄą╗čīąĮąŠą╣ ąĮą░ą│čĆčāąĘą║ąĖ ąĮą░ ąøą¤ą×. ą¤čĆąĖą╝ąĄąĮąĖč鹥ą╗čīąĮąŠ ą║ ąĖčüčüą╗ąĄą┤čāąĄą╝ąŠą╝čā čĆą░čüą┐čĆąĄą┤ąĄą╗ąĄąĮąĖčÄ ą┤ąĄč乊čĆą╝ą░čåąĖą╣ ąĖ ą┐ąĄčĆąĄą╝ąĄčēąĄąĮąĖą╣ čéą░ą║ąČąĄ ą┐čĆąĄą┤čüčéą░ą▓ą╗čÅčÄčé ąĖąĮč鹥čĆąĄčü čü č鹊čćą║ąĖ ąĘčĆąĄąĮąĖčÅ ą┤ą░ą╗čīąĮąĄą╣čłąĖčģ ąĖčüčüą╗ąĄą┤ąŠą▓ą░ąĮąĖą╣, ąĮą░ą┐čĆą░ą▓ą╗ąĄąĮąĮčŗčģ ąĮą░ ą╝ąŠą┤ąĖčäąĖą║ą░čåąĖčÄ č乊čĆą╝čāą╗čŗ (1). ą×ą┤ąĮą░ą║ąŠ čĆą░čüą┐čĆąĄą┤ąĄą╗ąĄąĮąĖąĄ ą┐ąĄčĆąĄą╝ąĄčēąĄąĮąĖą╣ ą▓ ąŠą▒čŖąĄą╝ąĄ ąĘą░ą╝ąŠčĆąŠąČąĄąĮąĮčŗčģ ą┐ąŠčĆąŠą┤ ąĮąĄ ą╝ąŠąČąĄčé ą▒čŗčéčī ą┐ąŠą╗čāč湥ąĮąŠ ą▓ ą░ąĮą░ą╗ąĖčéąĖč湥čüą║ąŠą╣ č乊čĆą╝ąĄ, ą┐ąŠčŹč鹊ą╝čā ąĮąĄąŠą▒čģąŠą┤ąĖą╝ąŠ čĆąĄčłąĖčéčī ąĘą░ą┤ą░čćčā (4)-(10) čćąĖčüą╗ąĄąĮąĮąŠ. ąÆ čüą▓ąŠčÄ ąŠč湥čĆąĄą┤čī, ą┤ą╗čÅ čĆą░ąĘčĆą░ą▒ąŠčéą║ąĖ čćąĖčüą╗ąĄąĮąĮąŠą╣ čüčģąĄą╝čŗ čĆą░čüč湥čéą░ ą┐ąŠčéčĆąĄą▒ąŠą▓ą░ą╗ąŠčüčī ą▓ąĖą┤ąŠąĖąĘą╝ąĄąĮąĖčéčī ąĖ ą┤ąŠą┐ąŠą╗ąĮąĖčéčī čüąĖčüč鹥ą╝čā čāčĆą░ą▓ąĮąĄąĮąĖą╣ (4)-(10) ą░čüčüąŠčåąĖąĖčĆąŠą▓ą░ąĮąĮčŗą╝ ąĘą░ą║ąŠąĮąŠą╝ ą┐ą╗ą░čüčéąĖč湥čüą║ąŠą│ąŠ č鹥č湥ąĮąĖčÅ [32, 33]:
ą░ ąĘą░ą║ąŠąĮ ąōčāą║ą░ (6)-(7) ą┐ąĄčĆąĄą┐ąĖčüą░čéčī ą▓ čüą╗ąĄą┤čāčÄčēąĄą╝ ą▓ąĖą┤ąĄ:
ą│ą┤ąĄ ╬Ąr(p),╬Ą╬Ė(p) ŌĆō ą┐ą╗ą░čüčéąĖč湥čüą║ąĖąĄ čćą░čüčéąĖ čĆą░ą┤ąĖą░ą╗čīąĮąŠą╣ ąĖ čéą░ąĮą│ąĄąĮčåąĖą░ą╗čīąĮąŠą╣ ą║ąŠą╝ą┐ąŠąĮąĄąĮčé č鹥ąĮąĘąŠčĆą░ ą┤ąĄč乊čĆą╝ą░čåąĖą╣ čüąŠąŠčéą▓ąĄčéčüčéą▓ąĄąĮąĮąŠ; ╬╗ ŌĆō ą┐ą╗ą░čüčéąĖč湥čüą║ąĖąĄ ą╝ąĮąŠąČąĖč鹥ą╗čī; F ŌĆō ą┐ąŠą▓ąĄčĆčģąĮąŠčüčéčī č鹥ą║čāč湥čüčéąĖ, ąŠą┐čĆąĄą┤ąĄą╗čÅąĄą╝ą░čÅ čāčüą╗ąŠą▓ąĖąĄą╝ (8).
ą¤čĆąĄą┤ą┐ąŠą╗ą░ą│ą░ąĄčéčüčÅ, čćč鹊 čāą▓ąĄą╗ąĖč湥ąĮąĖąĄ ą┐ą╗ą░čüčéąĖč湥čüą║ąĖčģ ą┤ąĄč乊čĆą╝ą░čåąĖą╣ ą▓ ąĘąŠąĮąĄ ą┐ą╗ą░čüčéąĖč湥čüą║ąŠą│ąŠ č鹥č湥ąĮąĖčÅ ą┐čĆąŠąĖčüčģąŠą┤ąĖčé ą▓ čüąŠąŠčéą▓ąĄčéčüčéą▓ąĖąĖ čü ą░čüčüąŠčåąĖąĖčĆąŠą▓ą░ąĮąĮčŗą╝ ąĘą░ą║ąŠąĮąŠą╝ č鹥č湥ąĮąĖčÅ. ąŚą░ą║ąŠąĮ ą┤ąŠčüčéą░č鹊čćąĮąŠ ą┐čĆąŠčüč鹊ą╣, ąŠą┤ąĮą░ą║ąŠ ą▓ ąĄą│ąŠ ąŠčüąĮąŠą▓ąĄ ą╗ąĄąČąĖčé čĆčÅą┤ čāą┐čĆąŠčēąĄąĮąĖą╣, ąĮąĄ ą▓ ą┐ąŠą╗ąĮąŠą╣ ą╝ąĄčĆąĄ čüą┐čĆą░ą▓ąĄą┤ą╗ąĖą▓čŗčģ ą┤ą╗čÅ ą│ąŠčĆąĮčŗčģ ą┐ąŠčĆąŠą┤ [34]. ąŁč鹊 ą║ą░čüą░ąĄčéčüčÅ ą┤ąŠą┐čāčēąĄąĮąĖčÅ ąŠ čüąŠąŠčüąĮąŠčüčéąĖ ą▓ąĄą║č鹊čĆąŠą▓ ą│ą╗ą░ą▓ąĮčŗčģ ąĮą░ą┐čĆčÅąČąĄąĮąĖą╣, ą╗ąĖąĮąĄą╣ąĮčŗčģ ąĖ ą┐ą╗ą░čüčéąĖč湥čüą║ąĖčģ čüąŠčüčéą░ą▓ą╗čÅčÄčēąĖčģ ą│ą╗ą░ą▓ąĮčŗčģ ą┤ąĄč乊čĆą╝ą░čåąĖą╣ [35]. ąöą╗čÅ čĆą░čüčüą╝ą░čéčĆąĖą▓ą░ąĄą╝ąŠą│ąŠ čüą╗čāčćą░čÅ čü ąĮčāą╗ąĄą▓čŗą╝ąĖ ą║ą░čüą░č鹥ą╗čīąĮčŗą╝ąĖ ą║ąŠą╝ą┐ąŠąĮąĄąĮčéą░ą╝ąĖ č鹥ąĮąĘąŠčĆąŠą▓ ąĮą░ą┐čĆčÅąČąĄąĮąĖą╣ ąĖ ą┤ąĄč乊čĆą╝ą░čåąĖą╣ ą┤ąŠą┐čāčēąĄąĮąĖąĄ ąŠ čüąŠąŠčüąĮąŠčüčéąĖ ą▓ąĄą║č鹊čĆąŠą▓ čüą┐čĆą░ą▓ąĄą┤ą╗ąĖą▓ąŠ.
ą¦ąĖčüą╗ąĄąĮąĮąŠąĄ čĆąĄčłąĄąĮąĖąĄ ąĘą░ą┤ą░čć (4), (7)-(13) ąŠčüčāčēąĄčüčéą▓ą╗čÅą╗ąŠčüčī ą┐čĆąĖ ą┐ąŠą╝ąŠčēąĖ ą¤ą× Wolfram Mathematica ą╝ąĄč鹊ą┤ąŠą╝ ą║ąŠąĮąĄčćąĮčŗčģ čĆą░ąĘąĮąŠčüč鹥ą╣. ąØą░ą│čĆčāąČąĄąĮąĖąĄ ąøą¤ą× ą▓čŗą┐ąŠą╗ąĮčÅą╗ąŠčüčī ąĖč鹥čĆą░čåąĖąŠąĮąĮąŠ. ąØą░ ą║ą░ąČą┤ąŠą╝ čłą░ą│ąĄ ąĖč鹥čĆą░čåąĖąĖ i = 1, ŌĆ” n ą║ ą▓ąĮąĄčłąĮąĄą╣ ą│čĆą░ąĮąĖčåąĄ ąøą¤ą× ą┐čĆąĖą▒ą░ą▓ą╗čÅą╗ą░čüčī ąĮą░ą│čĆčāąĘą║ą░, čĆą░ą▓ąĮą░čÅ ╬öPi= P/n. ąöą░ą╗ąĄąĄ ą▓ ą║ą░ąČą┤ąŠą╣ čÅč湥ą╣ą║ąĄ čĆą░čüč湥čéąĮąŠą╣ ąŠą▒ą╗ą░čüčéąĖ ą┐čĆąŠą▓ąĄčĆčÅą╗ąŠčüčī ą▓čŗą┐ąŠą╗ąĮąĄąĮąĖąĄ čāčüą╗ąŠą▓ąĖčÅ
ąĖ ą┐čĆąĖ ąĄą│ąŠ ąĮą░čĆčāčłąĄąĮąĖąĖ čĆą░čüčüčćąĖčéčŗą▓ą░ą╗čüčÅ ą┐čĆąĖčĆąŠčüčé ą┐ą╗ą░čüčéąĖč湥čüą║ąŠą╣ čćą░čüčéąĖ č鹥ąĮąĘąŠčĆą░ ą┤ąĄč乊čĆą╝ą░čåąĖą╣ ą▓ čüąŠąŠčéą▓ąĄčéčüčéą▓ąĖąĖ čü ąĘą░ą║ąŠąĮąŠą╝ (11).
ąĪą╗čāčćą░ą╣ ąŠą│čĆą░ąĮąĖč湥ąĮąĮąŠą╣ ą▓čŗčüąŠčéčŗ ąĘą░čģąŠą┤ą║ąĖ
ąĪą╗ąĄą┤čāčÄčēąĖą╝ čŹčéą░ą┐ąŠą╝ ąĖčüčüą╗ąĄą┤ąŠą▓ą░ąĮąĖčÅ ą▒čŗą╗ ą░ąĮą░ą╗ąĖąĘ ąØąöąĪ ąøą¤ą× ą┤ą╗čÅ ąŠą│čĆą░ąĮąĖč湥ąĮąĮąŠą╣ ą▓čŗčüąŠčéčŗ ąĘą░čģąŠą┤ą║ąĖ, ą║ąŠč鹊čĆčāčÄ ą╝ąŠąČąĮąŠ čāč湥čüčéčī ą┐čāč鹥ą╝ ąĮąĄą▒ąŠą╗čīčłąŠą╣ ą╝ąŠą┤ąĖčäąĖą║ą░čåąĖąĖ ąĖčüčģąŠą┤ąĮąŠą│ąŠ čāčĆą░ą▓ąĮąĄąĮąĖčÅ čĆą░ą▓ąĮąŠą▓ąĄčüąĖčÅ (4) ŌĆō ą┤ąŠą▒ą░ą▓ą╗ąĄąĮąĖąĄą╝ ą┤ąŠą┐ąŠą╗ąĮąĖč鹥ą╗čīąĮąŠą│ąŠ čćą╗ąĄąĮą░, čāčćąĖčéčŗą▓ą░čÄčēąĄą│ąŠ ą║ą░čüą░č鹥ą╗čīąĮąŠąĄ ąĮą░ą┐čĆčÅąČąĄąĮąĖąĄ Žärz [8]:
ą│ą┤ąĄ z ŌĆō ą▓ąĄčĆčéąĖą║ą░ą╗čīąĮą░čÅ ą║ąŠąŠčĆą┤ąĖąĮą░čéą░, ą╝.
ąÆą░ąČąĮąŠ čāčćąĖčéčŗą▓ą░čéčī, čćč鹊 ą┐ąŠčÅą▓ą╗ąĄąĮąĖąĄ ą║ą░čüą░č鹥ą╗čīąĮčŗčģ ąĮą░ą┐čĆčÅąČąĄąĮąĖą╣ ąĖ ą┤ąĄč乊čĆą╝ą░čåąĖą╣ ą┐čĆąĖą▓ąŠą┤ąĖčé ą║ čāčéčĆą░č鹥 čüąĖą╝ą╝ąĄčéčĆąĖąĖ ąĘą░ą┤ą░čćąĖ ą▓ ą▓ąĄčĆčéąĖą║ą░ą╗čīąĮąŠą╝ ąĮą░ą┐čĆą░ą▓ą╗ąĄąĮąĖąĖ, ąĖ čüąŠčüč鹊čÅąĮąĖąĄ ąøą¤ą× čāąČąĄ ąĮąĄą╗čīąĘčÅ čĆą░čüčüą╝ą░čéčĆąĖą▓ą░čéčī ą║ą░ą║ ą┐ą╗ąŠčüą║ąŠą┤ąĄč乊čĆą╝ąĖčĆąŠą▓ą░ąĮąĮąŠąĄ.
ąöą╗čÅ ą░ąĮą░ą╗ąĖąĘą░ ąĖ ą┐ąŠą┤ą▒ąŠčĆą░ ą▓ąĖą┤ą░ čäčāąĮą║čåąĖąĖ Žärz (r, z) ą┐čĆąĖą╝ąĄąĮąĄąĮčŗ ą╝ąĄč鹊ą┤čŗ čćąĖčüą╗ąĄąĮąĮąŠą│ąŠ ą╝ąŠą┤ąĄą╗ąĖčĆąŠą▓ą░ąĮąĖčÅ ąØąöąĪ ą▓ ąøą¤ą× čü čāč湥č鹊ą╝ ą▓čĆą░čēą░č鹥ą╗čīąĮąŠą╣ čüąĖą╝ą╝ąĄčéčĆąĖąĖ ąĘą░ą┤ą░čćąĖ, ą┐ąŠąĘą▓ąŠą╗čÅčÄčēąĄą╣ čüąĮąĖąĘąĖčéčī ą┐čĆąŠčüčéčĆą░ąĮčüčéą▓ąĄąĮąĮčāčÄ čĆą░ąĘą╝ąĄčĆąĮąŠčüčéčī ąĘą░ą┤ą░čćąĖ čü 3D ą┤ąŠ 2D. ą¦ąĖčüą╗ąĄąĮąĮąŠąĄ čĆąĄčłąĄąĮąĖąĄ ą┤ą▓čāčģą╝ąĄčĆąĮąŠą╣ ąĘą░ą┤ą░čćąĖ ą┐ąŠą╗čāč湥ąĮąŠ čü ą┐ąŠą╝ąŠčēčīčÄ ą╝ąĄč鹊ą┤ą░ ą║ąŠąĮąĄčćąĮčŗčģ 菹╗ąĄą╝ąĄąĮč鹊ą▓ ą▓ ą┐čĆąŠą│čĆą░ą╝ą╝ąĮąŠą╝ ą┐ą░ą║ąĄč鹥 Free FEM++. ąÆ ą┤ąŠą┐ąŠą╗ąĮąĄąĮąĖąĄ ą║ čāčĆą░ą▓ąĮąĄąĮąĖčÄ čĆą░ą▓ąĮąŠą▓ąĄčüąĖčÅ (15) ą┐ąŠ čĆą░ą┤ąĖą░ą╗čīąĮąŠą╣ ąŠčüąĖ čāčćąĖčéčŗą▓ą░ą╗ąŠčüčī čāčĆą░ą▓ąĮąĄąĮąĖąĄ čĆą░ą▓ąĮąŠą▓ąĄčüąĖčÅ ą┐ąŠ ą▓ąĄčĆčéąĖą║ą░ą╗čīąĮąŠą╝čā ąĮą░ą┐čĆą░ą▓ą╗ąĄąĮąĖčÄ:
ą│ą┤ąĄ Žāz ŌĆō ą▓ąĄčĆčéąĖą║ą░ą╗čīąĮą░čÅ ą║ąŠą╝ą┐ąŠąĮąĄąĮčéą░ č鹥ąĮąĘąŠčĆą░ ąĮą░ą┐čĆčÅąČąĄąĮąĖą╣, ą¤ą░.
ąöą╗čÅ ą┐čĆąŠčüč鹊čéčŗ čĆą░čüčüą╝ąŠčéčĆąĄąĮą░ čāą┐čĆčāą│ą░čÅ ą┐ąŠčüčéą░ąĮąŠą▓ą║ą░ ąĘą░ą┤ą░čćąĖ. ąØą░ ąĮąĖąČąĮąĄą╝ č鹊čĆčåąĄ ąøą¤ą× ąĘą░ą┤ą░ą▓ą░ą╗ąŠčüčī čāčüą╗ąŠą▓ąĖąĄ ąĮčāą╗ąĄą▓čŗčģ ą▓ąĄčĆčéąĖą║ą░ą╗čīąĮčŗčģ ą┐ąĄčĆąĄą╝ąĄčēąĄąĮąĖą╣, ą░ ąĮą░ ą▓ąĄčĆčģąĮąĄą╝ ŌĆō ą┤ą▓ą░ ą▓ąŠąĘą╝ąŠąČąĮčŗčģ ą▓ą░čĆąĖą░ąĮčéą░ čĆą░čüč湥čéąĮąŠą╣ čüčģąĄą╝čŗ. ąÆ ą┐ąĄčĆą▓ąŠą╝ čüą╗čāčćą░ąĄ čäąĖą║čüąĖčĆąŠą▓ą░ą╗ąĖčüčī ą║ą░ą║ ą▓ąĄčĆčéąĖą║ą░ą╗čīąĮčŗąĄ, čéą░ą║ ąĖ ą│ąŠčĆąĖąĘąŠąĮčéą░ą╗čīąĮčŗąĄ ą┐ąĄčĆąĄą╝ąĄčēąĄąĮąĖčÅ (ą║ą╗ą░čüčüąĖč湥čüą║ą░čÅ ą┐ąŠčüčéą░ąĮąŠą▓ą║ą░ ąĪ.ąĪ.ąÆčÅą╗ąŠą▓ą░ [27], čĆąĖčü.2, ą░), ą░ ą▓ąŠ ą▓č鹊čĆąŠą╝ ŌĆō ą▓ąĄčĆčéąĖą║ą░ą╗čīąĮą░čÅ ąĮą░ą│čĆčāąĘą║ą░, čüąŠąŠčéą▓ąĄčéčüčéą▓čāčÄčēą░čÅ ą▓ąĄčüčā ą▓čŗčłąĄą╗ąĄąČą░čēąĖčģ ą┐ąŠčĆąŠą┤ (q = 1,29 ą£ą¤ą░, čĆąĖčü.2, ą▒), ą┐čĆąĖ čŹč鹊ą╝ ąĮą░ ą▓ąĮčāčéčĆąĄąĮąĮąĄą╣ ą║čĆą░ą╣ąĮąĄą╣ č鹊čćą║ąĄ ą▓ąĄčĆčģąĮąĄą│ąŠ č鹊čĆčåą░ (r= a) ąŠą▒ą░ ą┐ąĄčĆąĄą╝ąĄčēąĄąĮąĖčÅ čäąĖą║čüąĖčĆąŠą▓ą░ą╗ąĖčüčī. ąōčĆą░ąĮąĖčćąĮčŗąĄ čāčüą╗ąŠą▓ąĖčÅ ąĮą░ ą▓ąĄčĆčģąĮąĄą╝ č鹊čĆčåąĄ, čüąŠąŠčéą▓ąĄčéčüčéą▓čāčÄčēąĖąĄ ą▓č鹊čĆąŠą╣ čĆą░čüč湥čéąĮąŠą╣ čüčģąĄą╝ąĄ, ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ą╗ąĖčüčī čéą░ą║ąČąĄ ą▓ čĆą░ą▒ąŠčéą░čģ [24, 26] ąĖ, ą┐ąŠ ą╝ąĮąĄąĮąĖčÄ ą░ą▓č鹊čĆąŠą▓, čÅą▓ą╗čÅčÄčéčüčÅ ą▒ąŠą╗ąĄąĄ ąŠą▒ąŠčüąĮąŠą▓ą░ąĮąĮčŗą╝ąĖ čü č鹊čćą║ąĖ ąĘčĆąĄąĮąĖčÅ čäąĖąĘąĖą║ąĖ. ąóąĄą╝ ąĮąĄ ą╝ąĄąĮąĄąĄ, čĆą░čüčüą╝ąŠčéčĆąĄąĮąĖąĄ ą┐ąĄčĆą▓ąŠą╣ čĆą░čüč湥čéąĮąŠą╣ čüčģąĄą╝čŗ (ą║ą░ą║ ą▓č鹊čĆąŠčüč鹥ą┐ąĄąĮąĮąŠą╣) čéą░ą║ąČąĄ ą┐čĆąĄą┤čüčéą░ą▓ą╗čÅąĄčé ąĖąĮč鹥čĆąĄčü ą▓ ąŠčéąĮąŠčłąĄąĮąĖąĖ čüčĆą░ą▓ąĮąĖč鹥ą╗čīąĮąŠą│ąŠ ą░ąĮą░ą╗ąĖąĘą░ čĆą░ąĘą╗ąĖčćąĮčŗčģ čĆą░čüč湥čéąĮčŗčģ čüčģąĄą╝.
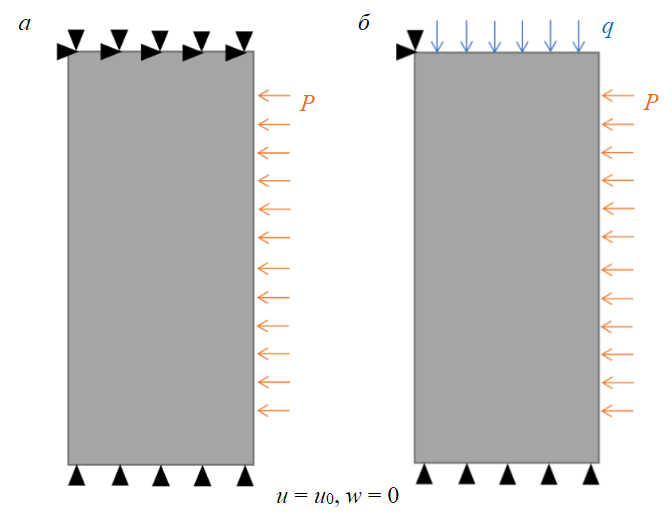
ąĀąĖčü.2. ąĀą░čüč湥čéąĮą░čÅ čüčģąĄą╝ą░ ą║ ą┤ą▓čāčģą╝ąĄčĆąĮąŠą╣ ąĘą░ą┤ą░č湥 ąØąöąĪ ą▓ ąøą¤ą×: a ŌĆō ą┐ąĄčĆą▓čŗą╣, ą▒ ŌĆō ą▓č鹊čĆąŠą╣ ą▓ą░čĆąĖą░ąĮčéčŗ
ąÆ čĆą░ą╝ą║ą░čģ ą┐ąĄčĆą▓ąŠą│ąŠ ą▓ą░čĆąĖą░ąĮčéą░ čĆą░čüč湥čéąĮąŠą╣ čüčģąĄą╝čŗ ą▓ąĄčĆčéąĖą║ą░ą╗čīąĮąŠąĄ ą┐ąĄčĆąĄą╝ąĄčēąĄąĮąĖąĄ w ąĘą░ą┤ą░ą▓ą░ą╗ąŠčüčī čĆą░ą▓ąĮčŗą╝ ąĮčāą╗čÄ, ą░ ą│ąŠčĆąĖąĘąŠąĮčéą░ą╗čīąĮąŠąĄ u ŌĆō čäčāąĮą║čåąĖąĄą╣ u0= a/r, čćč鹊 čäąĖąĘąĖč湥čüą║ąĖ ą╝ąŠąČąĮąŠ čéčĆą░ą║č鹊ą▓ą░čéčī ą║ą░ą║ ąĮąĄą║ąŠč鹊čĆąŠąĄ čĆą░ą▓ąĮąŠą▓ąĄčüąĮąŠąĄ čüą╝ąĄčēąĄąĮąĖąĄ ą▓ąĮčāčéčĆąĄąĮąĮąĄą╣ ą│čĆą░ąĮąĖčåčŗ ąøą¤ą×, ą┤ąŠčüčéąĖą│ąĮčāč鹊ąĄ ą▓ ą┤ą░ąĮąĮąŠą╝ ą│ąŠčĆąĖąĘąŠąĮčéą░ą╗čīąĮąŠą╝ čüąĄč湥ąĮąĖąĖ ą┐ąŠčĆąŠą┤ąĮąŠą│ąŠ ą╝ą░čüčüąĖą▓ą░ ąĮą░ ą┐čĆąĄą┤čŗą┤čāčēąĄą╣ ąĘą░čģąŠą┤ą║ąĄ ą║ ą╝ąŠą╝ąĄąĮčéčā ą▓ąŠąĘą▓ąĄą┤ąĄąĮąĖčÅ ą▒ąĄč鹊ąĮąĮąŠą╣ ą║čĆąĄą┐ąĖ. ą¤čĆąĖąĮčÅč鹊, čćč鹊 ą┐ąĄčĆąĄą╝ąĄčēąĄąĮąĖąĄ ąĮą░ ą▓ąĮčāčéčĆąĄąĮąĮąĄą╣ ą│čĆą░ąĮąĖčåąĄ ąøą¤ą× čā ą▓ąĄčĆčģąĮąĄą│ąŠ č鹊čĆčåą░ ąøą¤ą× čĆą░ą▓ąĮąŠ u0 = 0,5 čüą╝. ąöą░ą╗ąĄąĄ ą▓ čüąŠąŠčéą▓ąĄčéčüčéą▓ąĖąĖ čü č乊čĆą╝ą░ą╗ąĖąĘą╝ąŠą╝ ą╝ąĄč鹊ą┤ą░ ą║ąŠąĮąĄčćąĮčŗčģ 菹╗ąĄą╝ąĄąĮč鹊ą▓ [36] ą┤ąĄą╗ą░ą╗čüčÅ ą┐ąĄčĆąĄčģąŠą┤ ą║ ą▓ą░čĆąĖą░čåąĖąŠąĮąĮąŠą╣ ą┐ąŠčüčéą░ąĮąŠą▓ą║ąĄ ąŠčüąĄčüąĖą╝ą╝ąĄčéčĆąĖčćąĮąŠą╣ ąĘą░ą┤ą░čćąĖ č鹥ąŠčĆąĖąĖ čāą┐čĆčāą│ąŠčüčéąĖ ąĖ ą▓ą▓ąŠą┤ąĖą╗ąĖčüčī čäčāąĮą║čåąĖąĖ č乊čĆą╝čŗ ŌĆō ą┐ąĄčĆą▓ąŠą│ąŠ ą┐ąŠčĆčÅą┤ą║ą░ ą┤ą╗čÅ ą┐ąĄčĆąĄą╝ąĄčēąĄąĮąĖą╣ ąĖ ąĮčāą╗ąĄą▓ąŠą│ąŠ ą┐ąŠčĆčÅą┤ą║ą░ ą┤ą╗čÅ ąĮą░ą┐čĆčÅąČąĄąĮąĖą╣.
ą×ą▒čüčāąČą┤ąĄąĮąĖąĄ čĆąĄąĘčāą╗čīčéą░č鹊ą▓
ąĪą╗čāčćą░ą╣ ąĮąĄąŠą│čĆą░ąĮąĖč湥ąĮąĮąŠą╣ ą▓čŗčüąŠčéčŗ ąĘą░čģąŠą┤ą║ąĖ
ąĀą░čüčüčćąĖčéą░ąĮąĮąŠąĄ čĆą░čüą┐čĆąĄą┤ąĄą╗ąĄąĮąĖąĄ ą░ą▒čüąŠą╗čÄčéąĮčŗčģ ą▓ąĄą╗ąĖčćąĖąĮ čĆą░ą┤ąĖą░ą╗čīąĮčŗčģ ą┐ąĄčĆąĄą╝ąĄčēąĄąĮąĖą╣ ą▓ ąŠą▒čŖąĄą╝ąĄ ąøą¤ą× ą┐čĆąĄą┤čüčéą░ą▓ą╗ąĄąĮąŠ ąĮą░ čĆąĖčü.3. ąöąĄą╣čüčéą▓ąĖč鹥ą╗čīąĮčŗąĄ čĆą░ą┤ąĖą░ą╗čīąĮčŗąĄ ą┐ąĄčĆąĄą╝ąĄčēąĄąĮąĖčÅ ąĖą╝ąĄčÄčé ąŠčéčĆąĖčåą░č鹥ą╗čīąĮčŗą╣ ąĘąĮą░ą║. ąĀą░čüč湥čé ą┐čĆąŠąĖąĘą▓ąŠą┤ąĖą╗čüčÅ ą┤ą╗čÅ čüą╗ąĄą┤čāčÄčēąĖčģ ą┐ą░čĆą░ą╝ąĄčéčĆąŠą▓ ąĘą░ą┤ą░čćąĖ: P = 0,86 ą£ą¤ą░; K= 981 ą£ą¤ą░; G = 869 ą£ą¤ą░; ╬ø= 1,58; ╬ø┬» = 4,02 ą£ą¤ą░; a= 5 ą╝; b = 6,12 ą╝, čćč鹊 čüąŠąŠčéą▓ąĄčéčüčéą▓čāąĄčé ą░ą╗ąĄą▓čĆąĖčéčā [5]. ą¤ąŠą╝ąĖą╝ąŠ ą║čĆąĖą▓ąŠą╣ ą┤ą╗čÅ čāą┐čĆčāą│ąŠą┐ą╗ą░čüčéąĖč湥čüą║ąŠą│ąŠ ą┤ąĄč乊čĆą╝ąĖčĆąŠą▓ą░ąĮąĖčÅ ąøą¤ą× ą┐čĆąĄą┤čüčéą░ą▓ą╗ąĄąĮčŗ ą║čĆąĖą▓čŗąĄ ą┤ą╗čÅ čāą┐čĆčāą│ąŠą│ąŠ ą┤ąĄč乊čĆą╝ąĖčĆąŠą▓ą░ąĮąĖčÅ ąøą¤ą× ą┐čĆąĖ ąĮą░ą│čĆčāąĘą║ąĄ, čüąŠąŠčéą▓ąĄčéčüčéą▓čāčÄčēąĄą╣ ą▓ąŠąĘąĮąĖą║ąĮąŠą▓ąĄąĮąĖčÄ ąĘąŠąĮčŗ ą┐ą╗ą░čüčéąĖč湥čüą║ąĖčģ ą┤ąĄč乊čĆą╝ą░čåąĖą╣.
ąĀąĖčü.3. ąĀą░čüą┐čĆąĄą┤ąĄą╗ąĄąĮąĖąĄ ą░ą▒čüąŠą╗čÄčéąĮčŗčģ ąĘąĮą░č湥ąĮąĖą╣ čĆą░ą┤ąĖą░ą╗čīąĮčŗčģ ą┐ąĄčĆąĄą╝ąĄčēąĄąĮąĖą╣ ą▓ ąŠą▒čŖąĄą╝ąĄ ąøą¤ą× 1 ŌĆō ąĮą░čćą░ą╗ąŠ ąĘą░čĆąŠąČą┤ąĄąĮąĖčÅ ą┐ą╗ą░čüčéąĖč湥čüą║ąĖčģ ą┤ąĄč乊čĆą╝ą░čåąĖą╣; 2 ŌĆō ą┐čĆąĄą┤ąĄą╗čīąĮąŠąĄ čüąŠčüč鹊čÅąĮąĖąĄ čĆą░ą▓ąĮąŠą▓ąĄčüąĖčÅ (čāą┐čĆčāą│ąŠą┐ą╗ą░čüčéąĖč湥čüą║ąŠąĄ ą┤ąĄč乊čĆą╝ąĖčĆąŠą▓ą░ąĮąĖąĄ); 3 ŌĆō ą┐čĆąĄą┤ąĄą╗čīąĮąŠąĄ čüąŠčüč鹊čÅąĮąĖąĄ čĆą░ą▓ąĮąŠą▓ąĄčüąĖčÅ (čāą┐čĆčāą│ąŠąĄ ą┤ąĄč乊čĆą╝ąĖčĆąŠą▓ą░ąĮąĖąĄ)
ą£ąĖąĮąĖą╝ą░ą╗čīąĮčŗąĄ (ą┐ąŠ ą╝ąŠą┤čāą╗čÄ) ą┐ąĄčĆąĄą╝ąĄčēąĄąĮąĖčÅ čüąŠąŠčéą▓ąĄčéčüčéą▓čāčÄčé ąĮą░čćą░ą╗čā ąĘą░čĆąŠąČą┤ąĄąĮąĖčÅ ą┐ą╗ą░čüčéąĖč湥čüą║ąĖčģ ą┤ąĄč乊čĆą╝ą░čåąĖą╣ (ą▓ąĮąĄčłąĮčÅčÅ ąĮą░ą│čĆčāąĘą║ą░ ą▓ čŹč鹊ą╝ čüą╗čāčćą░ąĄ ąĮąĄčüą║ąŠą╗čīą║ąŠ ą╝ąĄąĮčīčłąĄ ąĖ čĆą░ą▓ąĮą░ 0,67 ą£ą¤ą░), ą░ ą╝ą░ą║čüąĖą╝ą░ą╗čīąĮčŗąĄ (ą┐ąŠ ą╝ąŠą┤čāą╗čÄ) ŌĆō čāą┐čĆčāą│ąŠą┐ą╗ą░čüčéąĖč湥čüą║ąŠą╝čā ą┤ąĄč乊čĆą╝ąĖčĆąŠą▓ą░ąĮąĖčÄ čü čāč湥č鹊ą╝ ą┐ą╗ą░čüčéąĖč湥čüą║ąŠą│ąŠ č鹥č湥ąĮąĖčÅ. ą¤čĆąĖ čŹč鹊ą╝ čĆą░čüą┐čĆąĄą┤ąĄą╗ąĄąĮąĖčÅ ą┐ąĄčĆąĄą╝ąĄčēąĄąĮąĖą╣ ą▓ąŠ ą▓čüąĄčģ čéčĆąĄčģ čüą╗čāčćą░čÅčģ čĆą░ą▓ąĮąŠą╝ąĄčĆąĮčŗ ą┐ąŠ č鹊ą╗čēąĖąĮąĄ ąøą¤ą×, ą░ ąŠčéąĮąŠčüąĖč鹥ą╗čīąĮą░čÅ čĆą░ąĘąĮąĖčåą░ ╬┤u ą╝ąĄąČą┤čā ą┐ąĄčĆąĄą╝ąĄčēąĄąĮąĖčÅą╝ąĖ ą▓ čāą┐čĆčāą│ąŠą╣ ąĖ ą▓ čāą┐čĆčāą│ąŠą┐ą╗ą░čüčéąĖč湥čüą║ąŠą╣ ą┐ąŠčüčéą░ąĮąŠą▓ą║ą░čģ ą┐čĆąĖ ą▓ąĮąĄčłąĮąĄą╣ ąĮą░ą│čĆčāąĘą║ąĄ 0,86 ą£ą¤ą░ čüąŠčüčéą░ą▓ą╗čÅąĄčé 34-39 % (ąŠčéąĮąŠčüąĖč鹥ą╗čīąĮąŠ ąĮą░ąĖą╝ąĄąĮčīčłąĄą│ąŠ ąĘąĮą░č湥ąĮąĖčÅ ą┐ąĄčĆąĄą╝ąĄčēąĄąĮąĖą╣). ąöą░ąĮąĮą░čÅ ą▓ąĄą╗ąĖčćąĖąĮą░ čüčāčēąĄčüčéą▓ąĄąĮąĮąŠ ąĘą░ą▓ąĖčüąĖčé ąŠčé čéąĖą┐ą░ ą┐ąŠčĆąŠą┤ ąĖ č鹥ą╝ą┐ąĄčĆą░čéčāčĆčŗ, ą┐čĆąĖ ą║ąŠč鹊čĆąŠą╣ ąŠą┐čĆąĄą┤ąĄą╗čÅą╗ąĖčüčī ą┐čĆąŠčćąĮąŠčüčéąĮčŗąĄ čģą░čĆą░ą║č鹥čĆąĖčüčéąĖą║ąĖ ąĘą░ą╝ąŠčĆąŠąČąĄąĮąĮčŗčģ ą┐ąŠčĆąŠą┤ (čüą╝. čéą░ą▒ą╗ąĖčåčā). ąöą░ąĮąĮčŗąĄ ą┐ąŠ čäąĖąĘąĖą║ąŠ-ą╝ąĄčģą░ąĮąĖč湥čüą║ąĖą╝ čüą▓ąŠą╣čüčéą▓ą░ą╝ ąĖ ą┤ą╗ąĖč鹥ą╗čīąĮąŠą╣ ą┐čĆąŠčćąĮąŠčüčéąĖ ą┐ąŠčĆąŠą┤ ą▓ąĘčÅčéčŗ ąĖąĘ ą╗ą░ą▒ąŠčĆą░č鹊čĆąĮčŗčģ ąĖčüčüą╗ąĄą┤ąŠą▓ą░ąĮąĖą╣ ą┐ąŠčĆąŠą┤ čüčéčĆąŠčÅčēąĄą│ąŠčüčÅ ą║ą░ą╗ąĖą╣ąĮąŠą│ąŠ čĆčāą┤ąĮąĖą║ą░, čćą░čüčéąĖčćąĮąŠ ąŠą┐ąĖčüą░ąĮąĮčŗčģ ą▓ čüčéą░čéčīąĄ [5]. ą¤čĆąŠčćąĮąŠčüčéąĮčŗąĄ čüą▓ąŠą╣čüčéą▓ą░ ╬ø ąĖ ╬ø┬» čüąŠąŠčéą▓ąĄčéčüčéą▓čāčÄčé ą┤ą╗ąĖč鹥ą╗čīąĮąŠčüčéąĖ ąĮą░ą│čĆčāąČąĄąĮąĖčÅ, čĆą░ą▓ąĮąŠą╣ 1 čüčāčé.
ą£ą░ą║čüąĖą╝ą░ą╗čīąĮą░čÅ ąŠčéąĮąŠčüąĖč鹥ą╗čīąĮą░čÅ čĆą░ąĘąĮąĖčåą░ ą┐ąĄčĆąĄą╝ąĄčēąĄąĮąĖą╣ ą▓ čāą┐čĆčāą│ąŠą╣ ąĖ čāą┐čĆčāą│ąŠą┐ą╗ą░čüčéąĖč湥čüą║ąŠą╣ ą┐ąŠčüčéą░ąĮąŠą▓ą║ą░čģ ą┤ą╗čÅ čĆą░ąĘą╗ąĖčćąĮčŗčģ čüą╗ąŠąĄą▓ ą┐ąŠčĆąŠą┤ ą┐ąŠ ą┤ą░ąĮąĮčŗą╝ čĆą░čüč湥č鹊ą▓
|
ąĪą╗ąŠą╣ |
╬ø |
╬ø┬», ą£ą¤ą░ |
K, ą£ą¤ą░ |
G, ą£ą¤ą░ |
P, ą£ą¤ą░ |
╬┤u, % |
|
ąÉą╗ąĄą▓čĆąĖčé |
1,58 |
4,02 |
981 |
869 |
0,86 |
39 |
|
ąĪčāą┐ąĄčüčī |
2,04 |
5,31 |
654 |
568 |
1,45 |
51 |
|
ą£ąĄą╗ |
1,52 |
4,18 |
890 |
800 |
1,68 |
57 |
|
ąōą╗ąĖąĮą░ |
1,38 |
3,75 |
950 |
860 |
2,5 |
71 |
ą£ą░ą║čüąĖą╝ą░ą╗čīąĮą░čÅ čĆą░ąĘąĮąĖčåą░ ╬┤u čĆą░ą┤ąĖą░ą╗čīąĮčŗčģ ą┐ąĄčĆąĄą╝ąĄčēąĄąĮąĖą╣ ą▓ ąŠą▒čŖąĄą╝ąĄ ąøą¤ą× ą▓ čāą┐čĆčāą│ąŠą╣ ąĖ ą▓ čāą┐čĆčāą│ąŠą┐ą╗ą░čüčéąĖč湥čüą║ąŠą╣ ą┐ąŠčüčéą░ąĮąŠą▓ą║ą░čģ čÅą▓ą╗čÅąĄčéčüčÅ ą▓ą░ąČąĮčŗą╝ ą┐ą░čĆą░ą╝ąĄčéčĆąŠą╝, ą║ąŠč鹊čĆčŗą╣ ą▒čāą┤ąĄčé ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮ ą┐čĆąĖ ą┤ą░ą╗čīąĮąĄą╣čłąĄą╝ ą░ąĮą░ą╗ąĖąĘąĄ ą┐ąŠčüčéą░ąĮąŠą▓ą║ąĖ (4)-(10) ąĖ ąĄąĄ čāčüą╗ąŠąČąĮąĄąĮąĖąĖ (15). ąöą╗čÅ čāą┐čĆčāą│ąŠą│ąŠ ą┤ąĄč乊čĆą╝ąĖčĆąŠą▓ą░ąĮąĖčÅ ąøą¤ą× čüčāčēąĄčüčéą▓čāąĄčé ą░ąĮą░ą╗ąĖčéąĖč湥čüą║ą░čÅ č乊čĆą╝čāą╗ą░ ą┤ą╗čÅ čĆą░čüč湥čéą░ ą║ą░ą║ čäčāąĮą║čåąĖąĖ ą┐ąĄčĆąĄą╝ąĄčēąĄąĮąĖą╣ u(r) [8], čéą░ą║ ąĖ, ą▓ čćą░čüčéąĮąŠčüčéąĖ, ą╝ą░ą║čüąĖą╝ą░ą╗čīąĮąŠą│ąŠ ąĘąĮą░č湥ąĮąĖčÅ ą┐ąĄčĆąĄą╝ąĄčēąĄąĮąĖčÅ ąĘą░ą╝ąŠčĆąŠąČąĄąĮąĮčŗčģ ą┐ąŠčĆąŠą┤ (ą┐ąŠ ą╝ąŠą┤čāą╗čÄ), ą┤ąŠčüčéąĖą│ą░ąĄą╝ąŠą│ąŠ ąĮą░ ą│čĆą░ąĮąĖčåąĄ r= a:
ą│ą┤ąĄ ╬Į ŌĆō ą║ąŠčŹčäčäąĖčåąĖąĄąĮčé ą¤čāą░čüčüąŠąĮą░; ąĀŌĆ▓ ŌĆō ą▓ąĮąĄčłąĮčÅčÅ ąĮą░ą│čĆčāąĘą║ą░.
ą¤čĆąĖ ą▓čŗą▓ąŠą┤ąĄ ąĖč鹊ą│ąŠą▓ąŠą│ąŠ ą▓čŗčĆą░ąČąĄąĮąĖčÅ ą▓ čāčĆą░ą▓ąĮąĄąĮąĖąĖ (17) čāčćąĖčéčŗą▓ą░ą╗ą░čüčī ąĖąĘą▓ąĄčüčéąĮą░čÅ ąĘą░ą▓ąĖčüąĖą╝ąŠčüčéčī ąŠą▒čŖąĄą╝ąĮąŠą│ąŠ ą╝ąŠą┤čāą╗čÅ čāą┐čĆčāą│ąŠčüčéąĖ ąŠčé ą╝ąŠą┤čāą╗čÅ čüą┤ą▓ąĖą│ą░ ąĖ ą║ąŠčŹčäčäąĖčåąĖąĄąĮčéą░ ą¤čāą░čüčüąŠąĮą░ (K = 2G(1 + ╬Į)/3/(1 ŌĆō 2╬Į)).
ąöą╗čÅ čāą┐čĆčāą│ąĖčģ ą┤ąĄč乊čĆą╝ą░čåąĖą╣ ą╝ą░ą║čüąĖą╝ą░ą╗čīąĮąŠąĄ ą┐ąĄčĆąĄą╝ąĄčēąĄąĮąĖąĄ ą╗ąĖąĮąĄą╣ąĮąŠ ąĘą░ą▓ąĖčüąĖčé ąŠčé ą▓ąĮąĄčłąĮąĄą╣ ąĮą░ą│čĆčāąĘą║ąĖ ąĀŌĆ▓. ą¤čĆąĖ čāą┐čĆčāą│ąŠą┐ą╗ą░čüčéąĖč湥čüą║ąŠą╝ ą┤ąĄč乊čĆą╝ąĖčĆąŠą▓ą░ąĮąĖąĖ ąøą¤ą× ąĘą░ą▓ąĖčüąĖą╝ąŠčüčéčī čāąČąĄ ąĮąĄ ą▒čāą┤ąĄčé čüą┐čĆą░ą▓ąĄą┤ą╗ąĖą▓ą░. ą×čåąĄąĮą║ą░ ą┤ą╗čÅ ą╝ą░ą║čüąĖą╝ą░ą╗čīąĮąŠą│ąŠ čüą╝ąĄčēąĄąĮąĖčÅ ą▓ąĮčāčéčĆąĄąĮąĮąĄą╣ čüč鹥ąĮą║ąĖ ąøą¤ą× ą║ čåąĄąĮčéčĆčā čüčéą▓ąŠą╗ą░ ą┤ą╗čÅ čāą┐čĆčāą│ąŠą┐ą╗ą░čüčéąĖč湥čüą║ąŠą│ąŠ čüą╗čāčćą░čÅ ą╝ąŠąČąĄčé ą▒čŗčéčī čüą┤ąĄą╗ą░ąĮą░ ą┐čāč鹥ą╝ ą▓ą▓ąĄą┤ąĄąĮąĖčÅ ą▓ ą┐čĆą░ą▓čāčÄ čćą░čüčéčī čāčĆą░ą▓ąĮąĄąĮąĖčÅ (17) ą╝ąĮąŠąČąĖč鹥ą╗čÅ ╬Š = 1 + 0,01╬┤u, ąĘą░ą▓ąĖčüčÅčēąĄą│ąŠ ąŠčé ą┐ą░čĆą░ą╝ąĄčéčĆą░ ╬┤u, ą║ąŠč鹊čĆčŗą╣ čĆą░čüčüčćąĖčéą░ąĮ čĆą░ąĮąĄąĄ ąĖ ą┐čĆąĖą▓ąĄą┤ąĄąĮ ą▓ čéą░ą▒ą╗ąĖčåąĄ.
ąĪą╗čāčćą░ą╣ ąŠą│čĆą░ąĮąĖč湥ąĮąĮąŠą╣ ą▓čŗčüąŠčéčŗ ąĘą░čģąŠą┤ą║ąĖ
ą¦ąĖčüą╗ąĄąĮąĮąŠąĄ čĆąĄčłąĄąĮąĖąĄ ąĘą░ą┤ą░čćąĖ ąŠ ą┤ą▓čāčģą╝ąĄčĆąĮąŠą╝ ąŠčüąĄčüąĖą╝ą╝ąĄčéčĆąĖčćąĮąŠą╝ ą┤ąĄč乊čĆą╝ąĖčĆąŠą▓ą░ąĮąĖąĖ ąøą¤ą× ą║ąŠąĮąĄčćąĮąŠą╣ ą▓čŗčüąŠčéčŗ ąĘą░čģąŠą┤ą║ąĖ ą┐čĆąĄą┤čüčéą░ą▓ą╗ąĄąĮąŠ ąĮą░ čĆąĖčü.4.
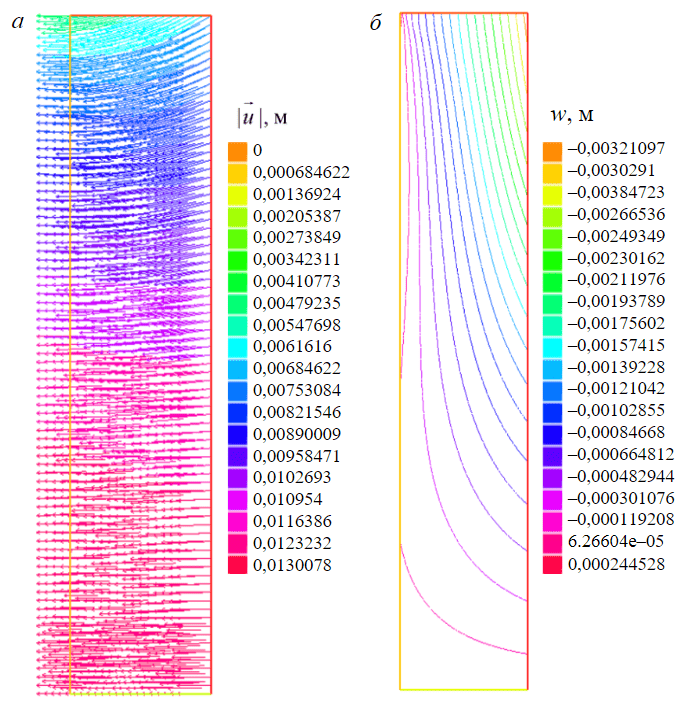
ąĀąĖčü.4. ą¦ąĖčüą╗ąĄąĮąĮąŠąĄ čĆąĄčłąĄąĮąĖąĄ ąĘą░ą┤ą░čćąĖ ąØąöąĪ ą▓ ąøą¤ą× ą┤ą╗čÅ ą▓č鹊čĆąŠą╣ čĆą░čüč湥čéąĮąŠą╣ čüčģąĄą╝čŗ: ą▓ąĄą║č鹊čĆąĮąŠąĄ ą┐ąŠą╗ąĄ ą┐ąŠą╗ąĮčŗčģ ą┐ąĄčĆąĄą╝ąĄčēąĄąĮąĖą╣ (ą░) ąĖ ą║ąŠąĮčéčāčĆąĮčŗąĄ ą╗ąĖąĮąĖąĖ ą▓ąĄčĆčéąĖą║ą░ą╗čīąĮčŗčģ ą┐ąĄčĆąĄą╝ąĄčēąĄąĮąĖą╣ (ą▒) ą▓ ą▓ąĄčĆčéąĖą║ą░ą╗čīąĮąŠą╝ čüąĄč湥ąĮąĖąĖ ąøą¤ą× ą▓čŗčüąŠč鹊ą╣ 5 ą╝
ąźą░čĆą░ą║č鹥čĆ ą┤ąĄč乊čĆą╝ąĖčĆąŠą▓ą░ąĮąĖčÅ ąøą¤ą× (čĆąĖčü.4) ą┐ąŠą║ą░ąĘčŗą▓ą░ąĄčé, čćč鹊 ą┐ąŠ ą░ą▒čüąŠą╗čÄčéąĮąŠą╣ ą▓ąĄą╗ąĖčćąĖąĮąĄ ą▓ąĄčĆčéąĖą║ą░ą╗čīąĮčŗąĄ ą┐ąĄčĆąĄą╝ąĄčēąĄąĮąĖčÅ ąĮą░ ą┐ąŠčĆčÅą┤ąŠą║ ąĮąĖąČąĄ čĆą░ą┤ąĖą░ą╗čīąĮčŗčģ ą┐ąĄčĆąĄą╝ąĄčēąĄąĮąĖą╣. ąÉ čĆą░ą┤ąĖą░ą╗čīąĮčŗąĄ ą┐ąĄčĆąĄą╝ąĄčēąĄąĮąĖčÅ čÅą▓ą╗čÅčÄčéčüčÅ čÅčĆą║ąŠ ą▓čŗčĆą░ąČąĄąĮąĮąŠą╣ čäčāąĮą║čåąĖąĄą╣ ą▓ąĄčĆčéąĖą║ą░ą╗čīąĮąŠą╣ ą║ąŠąŠčĆą┤ąĖąĮą░čéčŗ ŌĆō ą║ą░ą║ ą┤ą╗čÅ ą┐ąĄčĆą▓ąŠą│ąŠ ą▓ą░čĆąĖą░ąĮčéą░ čĆą░čüč湥čéąĮąŠą╣ čüčģąĄą╝čŗ (čĆąĖčü.5, ą░), čéą░ą║ ąĖ ą┤ą╗čÅ ą▓č鹊čĆąŠą│ąŠ (čĆąĖčü.5, ą▒). ąŁč鹊 čāą║ą░ąĘčŗą▓ą░ąĄčé ąĮą░ č鹊, čćč鹊 ą║ą░čüą░č鹥ą╗čīąĮąŠąĄ ąĮą░ą┐čĆčÅąČąĄąĮąĖąĄ Žärz Ōēł GŌłéu/Ōłéz čüčéą░ąĮąŠą▓ąĖčéčüčÅ ą▓ą░ąČąĮąĄą╣čłąĖą╝ čäą░ą║č鹊čĆąŠą╝, ą▓ąŠ ą╝ąĮąŠą│ąŠą╝ ąŠą┐čĆąĄą┤ąĄą╗čÅčÄčēąĖą╝ ąØąöąĪ ą▓ ąøą¤ą×, ą░ čéą░ą║ąČąĄ čĆą░ąĘą▓ąĖčéąĖąĄ ąĘąŠąĮčŗ ą┐ą╗ą░čüčéąĖč湥čüą║ąĖčģ ą┤ąĄč乊čĆą╝ą░čåąĖą╣.
ąÆąĄčĆčéąĖą║ą░ą╗čīąĮčŗąĄ ą┐ąĄčĆąĄą╝ąĄčēąĄąĮąĖčÅ ą╝ąĄąĮčÅčÄčéčüčÅ ą┐ąŠ ą▓čŗčüąŠč鹥 ąĮąĄąĘąĮą░čćąĖč鹥ą╗čīąĮąŠ, ąĘą░ ąĖčüą║ą╗čÄč湥ąĮąĖąĄą╝ ą╗ąŠą║ą░ą╗čīąĮčŗčģ ąŠą▒ą╗ą░čüč鹥ą╣ ąĮą░ ą▓ąĮąĄčłąĮąĄą╣ ąĖ ą▓ąĮčāčéčĆąĄąĮąĮąĄą╣ ą│čĆą░ąĮąĖčåą░čģ ąøą¤ą×. ą¤ąŠčŹč鹊ą╝čā ą┐ąĄčĆą▓čŗą╝ čüą╗ą░ą│ą░ąĄą╝čŗą╝ ą▓ čāčĆą░ą▓ąĮąĄąĮąĖąĖ (16) čćą░čüč鹊 ą┐čĆąĄąĮąĄą▒čĆąĄą│ą░čÄčé [26], č鹊ą│ą┤ą░
ą│ą┤ąĄ C(z) ŌĆō ąĮąĄą║ąŠč鹊čĆą░čÅ ąĮąĄąĖąĘą▓ąĄčüčéąĮą░čÅ čäčāąĮą║čåąĖčÅ ą║ąŠąŠčĆą┤ąĖąĮą░čéčŗ z.
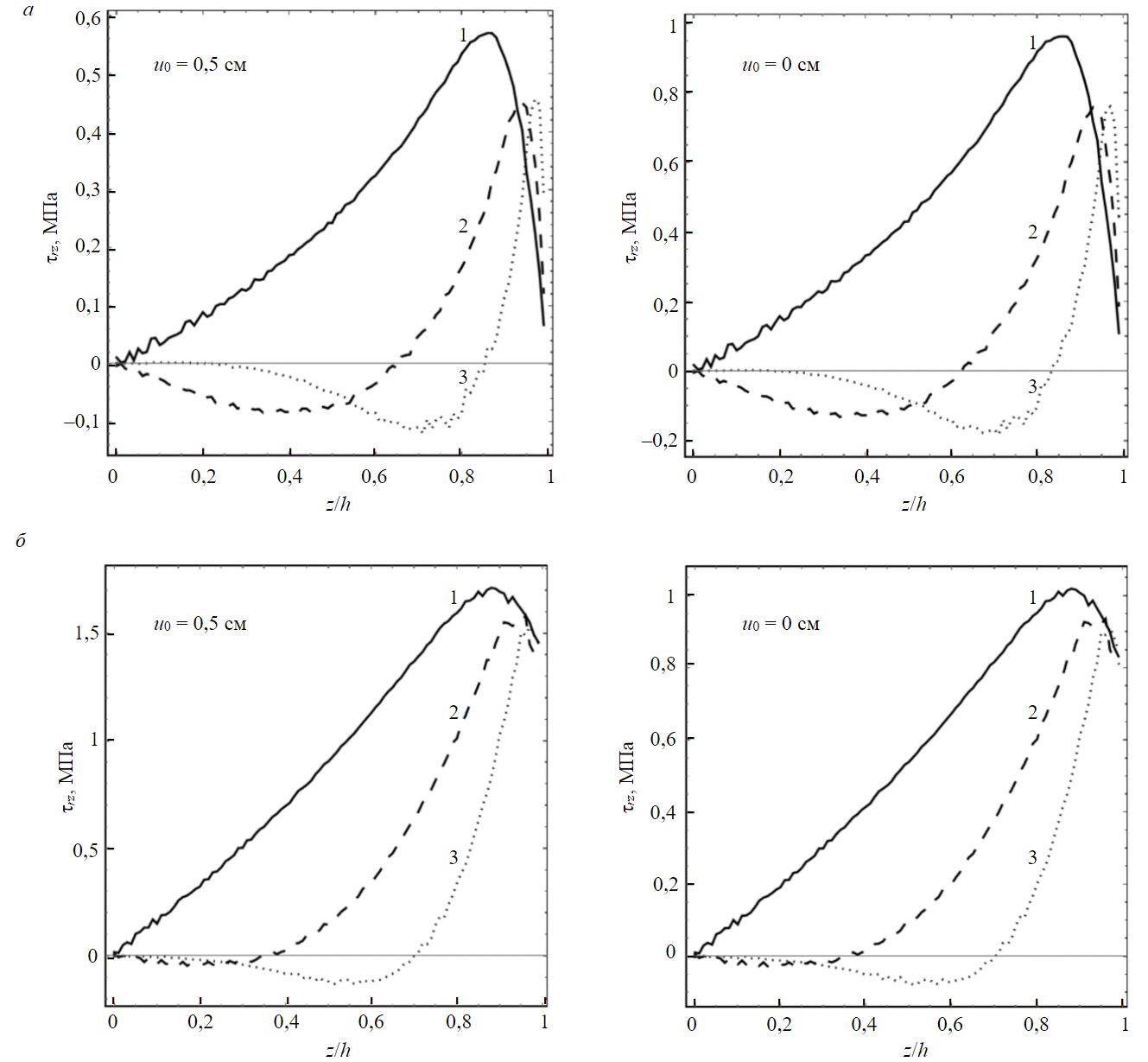
ąŚą░ą▓ąĖčüąĖą╝ąŠčüčéčī (18) ą▓ąĄčĆąĮą░ č鹊ą╗čīą║ąŠ ą┐čĆąĖą▒ą╗ąĖąČąĄąĮąĮąŠ, ą┐ąŠčüą║ąŠą╗čīą║čā ąĮą░ ą▓ąĮčāčéčĆąĄąĮąĮąĄą╣ ą│čĆą░ąĮąĖčåąĄ ąøą¤ą× ą║ą░čüą░č鹥ą╗čīąĮąŠąĄ ąĮą░ą┐čĆčÅąČąĄąĮąĖąĄ Žärz ą┤ąŠą╗ąČąĮąŠ ąŠą▒čĆą░čēą░čéčīčüčÅ ą▓ ąĮčāą╗čī. ąØą░ ą▓ąĮąĄčłąĮąĄą╣ ą│čĆą░ąĮąĖčåąĄ Žärz ą╝ąŠąČąĄčé ą║ą░ą║ ąŠą▒čĆą░čēą░čéčīčüčÅ ą▓ ąĮčāą╗čī, čéą░ą║ ąĖ ą▒čŗčéčī ąĮąĄ čĆą░ą▓ąĮčŗą╝ ąĮčāą╗čÄ ŌĆō ą▓ ąĘą░ą▓ąĖčüąĖą╝ąŠčüčéąĖ ąŠčé č鹊ą│ąŠ, ą║ą░ą║ ą▓ ą▓čŗą▒čĆą░ąĮąĮąŠą╣ čĆą░čüč湥čéąĮąŠą╣ čüčģąĄą╝ąĄ ą┐čĆąĖąĮčÅč鹊 čāčüą╗ąŠą▓ąĖąĄ ą║ąŠąĮčéą░ą║čéą░ ąĮąĄąĘą░ą╝ąŠčĆąŠąČąĄąĮąĮčŗčģ ą┐ąŠčĆąŠą┤ ąĖ ąøą¤ą×. ąÆ čĆą░čüčüą╝ą░čéčĆąĖą▓ą░ąĄą╝ąŠą╝ čüą╗čāčćą░ąĄ ą┐čĆąĖąĮčÅč鹊, čćč鹊 ą║ąŠąĮčéą░ą║čé ┬½čüą║ąŠą╗čīąĘčÅčēąĖą╣┬╗, ą░ ą┐ąŠč鹊ą╝čā ąĮą░ ą▓ąĮąĄčłąĮąĄą╣ ą│čĆą░ąĮąĖčåąĄ Žärz čéą░ą║ąČąĄ ą┤ąŠą╗ąČąĮąŠ ąŠą▒čĆą░čēą░čéčīčüčÅ ą▓ ąĮčāą╗čī.
ąÆąŠąĘąĮąĖą║ą░ąĄčé ą▓ąŠą┐čĆąŠčü, ą║ą░ą║ ąŠą┐čĆąĄą┤ąĄą╗ąĖčéčī čäčāąĮą║čåąĖčÄ ąĪ(z). ą¤ąŠ čĆąĄąĘčāą╗čīčéą░čéą░ą╝ čćąĖčüą╗ąĄąĮąĮąŠą│ąŠ ą╝ąŠą┤ąĄą╗ąĖčĆąŠą▓ą░ąĮąĖčÅ ą┤ą╗čÅ čüą╗čāčćą░čÅ ąĘą░ą┤ą░ąĮąĖčÅ ą▓ąĄčĆčéąĖą║ą░ą╗čīąĮąŠą╣ ąĮą░ą│čĆčāąĘą║ąĖ ąĮą░ ą▓ąĄčĆčģąĮąĄą╣ ą│čĆą░ąĮąĖčåąĄ ąøą¤ą× (čĆąĖčü.6, ą░) ąĘą░ą▓ąĖčüąĖą╝ąŠčüčéčī Žärz(z) ąĖą╝ąĄąĄčé čüą╗ąŠąČąĮčŗą╣ ąĮąĄą╗ąĖąĮąĄą╣ąĮčŗą╣ ąĖ ąĮąĄą╝ąŠąĮąŠč鹊ąĮąĮčŗą╣ čģą░čĆą░ą║č鹥čĆ. ąØą░ ą▓ąĄčĆčģąĮąĄą╣ ąĖ ąĮąĖąČąĮąĄą╣ ą│čĆą░ąĮąĖčåą░čģ ąøą¤ą× ą║ą░čüą░č鹥ą╗čīąĮąŠąĄ ąĮą░ą┐čĆčÅąČąĄąĮąĖąĄ ąŠą▒čĆą░čēą░ąĄčéčüčÅ ą▓ ąĮčāą╗čī, ą░ ą▓ąĮčāčéčĆąĖ ąøą¤ą× čäčāąĮą║čåąĖčÅ Žärz(z) ą╝ąŠąČąĄčé ąĖą╝ąĄčéčī ąŠą┤ąĖąĮ ąĖą╗ąĖ ą┤ą▓ą░ ą╗ąŠą║ą░ą╗čīąĮčŗčģ 菹║čüčéčĆąĄą╝čāą╝ą░. ą¤čĆąĖ čŹč鹊ą╝ ą┤ą░ąĮąĮą░čÅ čäčāąĮą║čåąĖčÅ čéą░ą║ąČąĄ čüčāčēąĄčüčéą▓ąĄąĮąĮąŠ ąĘą░ą▓ąĖčüąĖčé ąŠčé ą▓ąĄą╗ąĖčćąĖąĮčŗ u0 čüą╝ąĄčēąĄąĮąĖčÅ ą▓ąĮčāčéčĆąĄąĮąĮąĄą╣ čüč鹥ąĮą║ąĖ ąøą¤ą× čā ą▓ąĄčĆčģąĮąĄą│ąŠ č鹊čĆčåą░ ąøą¤ą×.
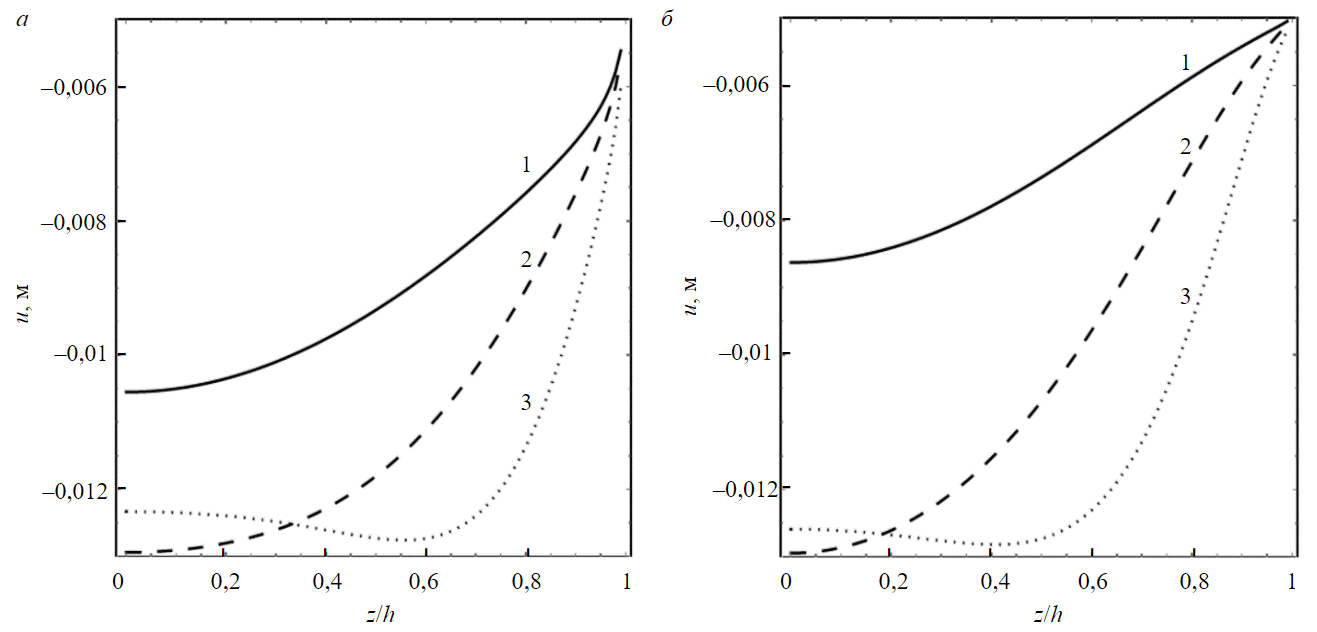
ąĀąĖčü.5. ąŚą░ą▓ąĖčüąĖą╝ąŠčüčéčī čĆą░ą┤ąĖą░ą╗čīąĮąŠą│ąŠ ą┐ąĄčĆąĄą╝ąĄčēąĄąĮąĖčÅ ąŠčé ą▓ąĄčĆčéąĖą║ą░ą╗čīąĮąŠą╣ ą║ąŠąŠčĆą┤ąĖąĮą░čéčŗ ąĮą░ ą▓ąĮčāčéčĆąĄąĮąĮąĄą╣ ą│čĆą░ąĮąĖčåąĄ ąøą¤ą× ą┤ą╗čÅ ą┐ąĄčĆą▓ąŠą╣ (ą░) ąĖ ą▓č鹊čĆąŠą╣ (ą▒) čĆą░čüč湥čéąĮčŗčģ čüčģąĄą╝
1 ŌĆō h = 2,5 ą╝; 2 ŌĆō h = 5 ą╝; 3 ŌĆō h =10 ą╝
ąĀąĖčü.6. ąŚą░ą▓ąĖčüąĖą╝ąŠčüčéčī ą║ą░čüą░č鹥ą╗čīąĮąŠą│ąŠ ąĮą░ą┐čĆčÅąČąĄąĮąĖčÅ Žärz ąŠčé ą▓ąĄčĆčéąĖą║ą░ą╗čīąĮąŠą╣ ą║ąŠąŠčĆą┤ąĖąĮą░čéčŗ ą┐čĆąĖ čĆą░ąĘą╗ąĖčćąĮčŗčģ ą▓čŗčüąŠčéą░čģ ąĘą░čģąŠą┤ą║ąĖ, čüčĆąĄą┤ąĖąĮąĮąŠąĄ čĆą░ą┤ąĖą░ą╗čīąĮąŠąĄ čüąĄč湥ąĮąĖąĄ ąøą¤ą×, čĆą░čüč湥čéąĮą░čÅ čüčģąĄą╝ą░ čü ą▓ąĄčĆčéąĖą║ą░ą╗čīąĮąŠą╣ ąĮą░ą│čĆčāąĘą║ąŠą╣ (ą░) ąĮą░ ą▓ąĄčĆčģąĮąĄą╝ č鹊čĆčåąĄ ąĖ čäąĖą║čüąĖčĆąŠą▓ą░ąĮąĮčŗą╝ąĖ ą┐ąĄčĆąĄą╝ąĄčēąĄąĮąĖčÅą╝ąĖ (ą▒)
ąōčĆą░ą┤ąĖąĄąĮčé ą║ą░čüą░č鹥ą╗čīąĮčŗčģ ąĮą░ą┐čĆčÅąČąĄąĮąĖą╣ ŌłéŽärz/Ōłéz, ą┐čĆąĖčüčāčéčüčéą▓čāčÄčēąĖą╣ ą▓ č乊čĆą╝čāą╗ąĄ (15), ąĘąĮą░ą║ąŠą┐ąĄčĆąĄą╝ąĄąĮąĄąĮ. ą×čüąŠą▒ąĄąĮąĮąŠ čÅčĆą║ąŠ čŹč鹊 ą┐čĆąŠčÅą▓ą╗čÅąĄčéčüčÅ ą┤ą╗čÅ čĆą░čüč湥čéąĮąŠą╣ čüčģąĄą╝čŗ čü ą▓ąĄčĆčéąĖą║ą░ą╗čīąĮąŠą╣ ąĮą░ą│čĆčāąĘą║ąŠą╣ (čĆąĖčü.6). ąÆą▒ą╗ąĖąĘąĖ ą▓ąĄčĆčģąĮąĄą│ąŠ č鹊čĆčåą░ ąøą¤ą× (z = h) ąŠąĮ ąĖą╝ąĄąĄčé ąŠčéčĆąĖčåą░č鹥ą╗čīąĮąŠąĄ ąĘąĮą░č湥ąĮąĖąĄ ąĖ ą╝ą░ą║čüąĖą╝ą░ą╗ąĄąĮ ą┐ąŠ ą╝ąŠą┤čāą╗čÄ, ą┐čĆąĖ z= 0,85-0,97h ą│čĆą░ą┤ąĖąĄąĮčé ąŠą▒čĆą░čēą░ąĄčéčüčÅ ą▓ ąĮčāą╗čī, ą░ ą┐čĆąĖ ą┤ą░ą╗čīąĮąĄą╣čłąĄą╝ čāą╝ąĄąĮčīčłąĄąĮąĖąĖ z ąŠąĮ ąĮą░ ąĮąĄą║ąŠč鹊čĆąŠą╝ ąŠčéčĆąĄąĘą║ąĄ čüąŠčģčĆą░ąĮčÅąĄčé ą┐ąŠą╗ąŠąČąĖč鹥ą╗čīąĮąŠąĄ ąĘąĮą░č湥ąĮąĖąĄ ąĖ čāą▒čŗą▓ą░ąĄčé ą┐ąŠ ą░ą▒čüąŠą╗čÄčéąĮąŠą╣ ą▓ąĄą╗ąĖčćąĖąĮąĄ, čéą░ą║ ą║ą░ą║ ą║čĆąĖą▓ą░čÅ Žärz(z) čüčéą░ąĮąŠą▓ąĖčéčüčÅ ą▒ąŠą╗ąĄąĄ ą┐ąŠą╗ąŠą│ąŠą╣. ąÆč鹊čĆąŠą╣ 菹║čüčéčĆąĄą╝čāą╝ (ąĄčüą╗ąĖ ąŠąĮ ąĄčüčéčī) ą┤ąŠčüčéąĖą│ą░ąĄčéčüčÅ ąĮą░ ą┐ąŠą╗ąŠą│ąŠą╝ čāčćą░čüčéą║ąĄ ą║čĆąĖą▓ąŠą╣ ąĖ ą┐ąŠč鹊ą╝čā ą▓čŗąĘčŗą▓ą░ąĄčé ą╝ąĄąĮčīčłąĖą╣ ąĖąĮč鹥čĆąĄčü. ą¤ąŠą┤ąŠą▒ąĮą░čÅ čüąĖčéčāą░čåąĖčÅ čüą║ą╗ą░ą┤čŗą▓ą░ąĄčéčüčÅ ą┤ą╗čÅ čĆą░čüč湥čéąĮąŠą╣ čüčģąĄą╝čŗ čü čäąĖą║čüąĖčĆąŠą▓ą░ąĮąĮčŗą╝ąĖ ą┐ąĄčĆąĄą╝ąĄčēąĄąĮąĖčÅą╝ąĖ ąĮą░ ą▓ąĄčĆčģąĮąĄą╝ č鹊čĆčåąĄ (čĆąĖčü.6, ą▒), ą┐čĆąĖ čŹč鹊ą╝ ą┤ą╗čÅ ą╝ą░ą╗čŗčģ ą▓čŗčüąŠčé ąĘą░čģąŠą┤ą║ąĖ ąĘą░ą▓ąĖčüąĖą╝ąŠčüčéčī ą║ą░čüą░č鹥ą╗čīąĮąŠą│ąŠ ąĮą░ą┐čĆčÅąČąĄąĮąĖčÅ ąŠčé ą▓ąĄčĆčéąĖą║ą░ą╗čīąĮąŠą╣ ą║ąŠąŠčĆą┤ąĖąĮą░čéčŗ z ą▒ą╗ąĖąĘą║ą░ ą║ ą╗ąĖąĮąĄą╣ąĮąŠą╣.
ąÆ čĆą░ą▒ąŠč鹥 [27] ą┤ą╗čÅ ą▓čŗą▓ąŠą┤ą░ č乊čĆą╝čāą╗čŗ č鹊ą╗čēąĖąĮčŗ ąøą¤ą× ą┐ąŠ ą║čĆąĖč鹥čĆąĖčÄ ą┐ąŠą╗ąĘčāč湥čüčéąĖ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ą╗ąŠčüčī ą┤ąŠą┐čāčēąĄąĮąĖąĄ ąŠ ą╗ąĖąĮąĄą╣ąĮąŠą╣ ąĘą░ą▓ąĖčüąĖą╝ąŠčüčéąĖ ą║ą░čüą░č鹥ą╗čīąĮąŠą│ąŠ ąĮą░ą┐čĆčÅąČąĄąĮąĖčÅ ąŠčé ą▓ąĄčĆčéąĖą║ą░ą╗čīąĮąŠą╣ ą║ąŠąŠčĆą┤ąĖąĮą░čéčŗ Žärz(z) = Az + B. ąøąĖąĮąĄą╣ąĮą░čÅ č乊čĆą╝ą░ ąĘą░ą▓ąĖčüąĖą╝ąŠčüčéąĖ ą┐čĆąĄą┤čüčéą░ą▓ą╗čÅąĄčé čüąŠą▒ąŠą╣ ą┐čĆąŠčüč鹊ą╣ ą┐ąŠą┤čģąŠą┤, čéčĆąĄą▒čāčÄčēąĖą╣ ą╝ąĖąĮąĖą╝ą░ą╗čīąĮąŠą│ąŠ čćąĖčüą╗ą░ ą┤ąŠą┐ąŠą╗ąĮąĖč鹥ą╗čīąĮčŗčģ čāčüą╗ąŠą▓ąĖą╣ ą┤ą╗čÅ ąŠą┐čĆąĄą┤ąĄą╗ąĄąĮąĖčÅ ąĮąĄąĖąĘą▓ąĄčüčéąĮčŗčģ ą║ąŠčŹčäčäąĖčåąĖąĄąĮč鹊ą▓ ąÉ ąĖ ąÆ. ąÜčĆąŠą╝ąĄ č鹊ą│ąŠ, čü čāč湥č鹊ą╝ čéą░ą║ąŠą╣ ąĘą░ą▓ąĖčüąĖą╝ąŠčüčéąĖ ą┐čĆąŠąĖąĘą▓ąŠą┤ąĮą░čÅ Žärz(z) ą┐ąŠ z ąŠčüčéą░ąĄčéčüčÅ ą┐ąŠčüč鹊čÅąĮąĮąŠą╣, ą░ ą┐ą░čĆą░ą╝ąĄčéčĆ z ąĖčüč湥ąĘą░ąĄčé ąĖąĘ čāčĆą░ą▓ąĮąĄąĮąĖčÅ (15), čćč鹊 čüčéą░ąĮąŠą▓ąĖčéčüčÅ čāą┤ąŠą▒ąĮčŗą╝ ą┐čĆąĖ č鹥ąŠčĆąĄčéąĖč湥čüą║ąŠą╝ ą░ąĮą░ą╗ąĖąĘąĄ.
ą¤čĆąĖ ą│čĆą░ąĮąĖčćąĮčŗčģ čāčüą╗ąŠą▓ąĖčÅčģ ąĮą░ ąĮąĖąČąĮąĄą╝ ąĖ ą▓ąĄčĆčģąĮąĄą╝ č鹊čĆčåą░čģ ąøą¤ą×
ą╗ąĖąĮąĄą╣ąĮą░čÅ čäčāąĮą║čåąĖčÅ ą║ą░čüą░č鹥ą╗čīąĮčŗčģ ąĮą░ą┐čĆčÅąČąĄąĮąĖą╣ ąŠčé z ą╝ąŠąČąĄčé ą▒čŗčéčī ą┐čĆąĄą┤čüčéą░ą▓ą╗ąĄąĮą░ ą▓ ą▓ąĖą┤ąĄ
ąÜąŠčŹčäčäąĖčåąĖąĄąĮčéą┐čĆąĖ z ą▓ ą╗ąĖąĮąĄą╣ąĮąŠą╣ ąĘą░ą▓ąĖčüąĖą╝ąŠčüčéąĖ Žärz(z) č乊čĆą╝čāą╗čŗ (21) ą┐ąŠą╗čāč湥ąĮ, ąĖčüčģąŠą┤čÅ ąĖąĘ čāčüą╗ąŠą▓ąĖčÅ ą╗ąĖąĮąĄą╣ąĮąŠą╣ ą▓ąĘą░ąĖą╝ąŠčüą▓čÅąĘąĖ Žärz, u*(r) ą▓ čāčĆą░ą▓ąĮąĄąĮąĖąĖ (20) čü ą╝ąŠą┤čāą╗ąĄą╝ G. ą¤čĆąĖ čŹč鹊ą╝ čĆą░ąĘą╝ąĄčĆąĮčŗą╣ ą│ąĄąŠą╝ąĄčéčĆąĖč湥čüą║ąĖą╣ ą┐ą░čĆą░ą╝ąĄčéčĆ (ah)ŌĆō1 ą┐ąŠą┤ąŠą▒čĆą░ąĮ čéą░ą║, čćč鹊ą▒čŗ ą┐ąŠą╗čāčćąĖčéčī ą┐čĆą░ą▓ąĖą╗čīąĮąŠąĄ ą░čüąĖą╝ą┐č鹊čéąĖč湥čüą║ąŠąĄ ą┐ąŠą▓ąĄą┤ąĄąĮąĖąĄ čĆąĄčłąĄąĮąĖčÅ čĆą░čüčüą╝ą░čéčĆąĖą▓ą░ąĄą╝ąŠą╣ ąĘą░ą┤ą░čćąĖ ą┐čĆąĖ ą╝ą░ą╗čŗčģ ąĘąĮą░č湥ąĮąĖčÅčģ h.
ąÆčŗčĆą░ąČąĄąĮąĖąĄ (21) ąĮą░čģąŠą┤ąĖčéčüčÅ ą▓ čģąŠčĆąŠčłąĄą╝ čüąŠąŠčéą▓ąĄčéčüčéą▓ąĖąĖ čü čāčüą╗ąŠą▓ąĖąĄą╝ (18), čāčüčéą░ąĮą░ą▓ą╗ąĖą▓ą░čÄčēąĖą╝ ąĘą░ą▓ąĖčüąĖą╝ąŠčüčéčī ą║ą░čüą░č鹥ą╗čīąĮąŠą│ąŠ ąĮą░ą┐čĆčÅąČąĄąĮąĖčÅ ąŠčé čĆą░ą┤ąĖą░ą╗čīąĮąŠą╣ ą║ąŠąŠčĆą┤ąĖąĮą░čéčŗ. ąĪ čāč湥č鹊ą╝ č乊čĆą╝čāą╗čŗ (21) čāčĆą░ą▓ąĮąĄąĮąĖąĄ (15) ą╝ąŠąČąĄčé ą▒čŗčéčī ąĘą░ą┐ąĖčüą░ąĮąŠ ą▓ čéą░ą║ąŠą╝ ą▓ąĖą┤ąĄ:
ąÆ čĆą░ą▒ąŠčéą░čģ [27, 37] čāčĆą░ą▓ąĮąĄąĮąĖąĄ (22) čĆąĄčłą░ą╗ąŠčüčī ą┐čāč鹥ą╝ ą┐ąŠą┤čüčéą░ąĮąŠą▓ą║ąĖ ą▓ ąĮąĄą│ąŠ ą▓čŗčĆą░ąČąĄąĮąĖčÅ ą┤ą╗čÅ Žā╬Ė ąĖąĘ ąĘą░ą║ąŠąĮą░ ą£ąŠčĆą░ ŌĆō ąÜčāą╗ąŠąĮą░ (8). ą¤ąŠą╗čāč湥ąĮąĮąŠąĄ ą┤ąĖčäč乥čĆąĄąĮčåąĖą░ą╗čīąĮąŠąĄ čāčĆą░ą▓ąĮąĄąĮąĖąĄ čüąŠą┤ąĄčƹȹ░ą╗ąŠ ąĄą┤ąĖąĮčüčéą▓ąĄąĮąĮčāčÄ ąĮąĄąĖąĘą▓ąĄčüčéąĮčāčÄ čäčāąĮą║čåąĖčÄ Žār ąĖ ą╝ąŠą│ą╗ąŠ ą▒čŗčéčī čĆąĄčłąĄąĮąŠ ą░ąĮą░ą╗ąĖčéąĖč湥čüą║ąĖ čü čāč湥č鹊ą╝ čāčüą╗ąŠą▓ąĖą╣ (9) ąĮą░ ą│čĆą░ąĮąĖčåą░čģ čĆą░čüč湥čéąĮąŠą╣ ąŠą▒ą╗ą░čüčéąĖ. ą×ą┤ąĮą░ą║ąŠ, ą┐čĆąĖąĮąĖą╝ą░čÅ ą▓ąŠ ą▓ąĮąĖą╝ą░ąĮąĖąĄ ąĮąĄąĮčāą╗ąĄą▓ąŠąĄ ą║ą░čüą░č鹥ą╗čīąĮąŠąĄ ąĮą░ą┐čĆčÅąČąĄąĮąĖąĄ Žärz, ąŠčüąĄą▓čŗąĄ ą║ąŠą╝ą┐ąŠąĮąĄąĮčéčŗ ąĮą░ą┐čĆčÅąČąĄąĮąĖą╣ ą▓ ąŠą▒čēąĄą╝ čüą╗čāčćą░ąĄ čāąČąĄ ąĮąĄ ą▒čāą┤čāčé čÅą▓ą╗čÅčéčīčüčÅ ą│ą╗ą░ą▓ąĮčŗą╝ąĖ ąĮą░ą┐čĆčÅąČąĄąĮąĖčÅą╝ąĖ. ąÉ ą▓ ąĘąŠąĮąĄ ą▓ąĄčĆčģąĮąĄą│ąŠ č鹊čĆčåą░ ąøą¤ą× čāą│ą╗ąŠą▓ąŠąĄ ąĮą░ą┐čĆčÅąČąĄąĮąĖąĄ čüčéą░ąĮąŠą▓ąĖčéčüčÅ ą▓č鹊čĆčŗą╝ ą│ą╗ą░ą▓ąĮčŗą╝ ąĮą░ą┐čĆčÅąČąĄąĮąĖąĄą╝ ąĖ, čüą╗ąĄą┤ąŠą▓ą░č鹥ą╗čīąĮąŠ, ąĮąĄ ą▓ą║ą╗čÄčćą░ąĄčéčüčÅ ą▓ ąŠą▒čēąĖą╣ ąĘą░ą║ąŠąĮ ą£ąŠčĆą░ ŌĆō ąÜčāą╗ąŠąĮą░, ą║ąŠč鹊čĆčŗą╣ ąĘą░ą┐ąĖčüčŗą▓ą░ąĄčéčüčÅ ą▓ ą▓ąĖą┤ąĄ:
ąÆ ąŠčéą╗ąĖčćąĖąĄ ąŠčé ąŠą▒ą╗ą░čüčéąĖ ą▓ąĄčĆčģąĮąĄą│ąŠ č鹊čĆčåą░ ąøą¤ą×, ą┤ą╗čÅ ą║ąŠč鹊čĆąŠą╣ ąĮąĄ čüčāčēąĄčüčéą▓čāąĄčé ą┐čĆąŠčüč鹊ą│ąŠ ą░ąĮą░ą╗ąĖčéąĖč湥čüą║ąŠą│ąŠ čĆąĄčłąĄąĮąĖčÅ, ą▓ ąŠą▒ą╗ą░čüčéąĖ ąĮąĖąČąĮąĄą│ąŠ č鹊čĆčåą░ ąøą¤ą× ą║ą░čüą░č鹥ą╗čīąĮąŠąĄ ąĮą░ą┐čĆčÅąČąĄąĮąĖąĄ čüčāčēąĄčüčéą▓ąĄąĮąĮąŠ ąĮąĖąČąĄ ą┤čĆčāą│ąĖčģ ą║ąŠą╝ą┐ąŠąĮąĄąĮčé č鹥ąĮąĘąŠčĆą░ ąĮą░ą┐čĆčÅąČąĄąĮąĖą╣, čāą│ą╗ąŠą▓ąŠąĄ ąĮą░ą┐čĆčÅąČąĄąĮąĖąĄ ą▓čŗčüčéčāą┐ą░ąĄčé ą▓ ą║ą░č湥čüčéą▓ąĄ ą┐ąĄčĆą▓ąŠą│ąŠ ą│ą╗ą░ą▓ąĮąŠą│ąŠ ąĮą░ą┐čĆčÅąČąĄąĮąĖčÅ Žā1. ąÆ čŹč鹊ą╝ čüą╗čāčćą░ąĄ čāčĆą░ą▓ąĮąĄąĮąĖąĄ (22) ąĖą╝ąĄąĄčé ą░ąĮą░ą╗ąĖčéąĖč湥čüą║ąŠąĄ čĆąĄčłąĄąĮąĖąĄ ą┤ą╗čÅ ą┐ąŠą╗čÅ ąĮą░ą┐čĆčÅąČąĄąĮąĖą╣ ą▓ čāčüą╗ąŠą▓ąĖčÅčģ ą┐čĆąĄą┤ąĄą╗čīąĮąŠą│ąŠ ąĮą░ą┐čĆčÅąČąĄąĮąĮąŠą│ąŠ čüąŠčüč鹊čÅąĮąĖčÅ, ą║ąŠą│ą┤ą░ ą▓ąŠ ą▓čüąĄą╝ ąŠą▒čŖąĄą╝ąĄ ą┐ąŠčĆąŠą┤čŗ ą▓čŗą┐ąŠą╗ąĮčÅąĄčéčüčÅ ąĘą░ą║ąŠąĮ ą£ąŠčĆą░ ŌĆō ąÜčāą╗ąŠąĮą░:
ąÆ č乊čĆą╝čāą╗ąĄ (25) ą▓ ą║ą░č湥čüčéą▓ąĄ ą┐ąĄčĆąĄą╝ąĄčēąĄąĮąĖčÅ ua ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ą╗ą░čüčī ąĘą░ą▓ąĖčüąĖą╝ąŠčüčéčī (17). ą¤čĆąĖ ą┐ąŠą┤čüčéą░ąĮąŠą▓ą║ąĄ čĆą░ą▓ąĄąĮčüčéą▓ (23) ąĖ (22) ą│ą╗ą░ą▓ąĮčŗąĄ ąĮą░ą┐čĆčÅąČąĄąĮąĖčÅ ąĘą░ą┐ąĖčüą░ąĮčŗ čüą╗ąĄą┤čāčÄčēąĖą╝ ąŠą▒čĆą░ąĘąŠą╝: Žā1 = Žā╬Ė, Žā3 = Žār. ąÜąŠčŹčäčäąĖčåąĖąĄąĮčé ╬Š Ōēź 1 ą▓ ą┤ą░ąĮąĮąŠą╝ čüą╗čāčćą░ąĄ čÅą▓ą╗čÅąĄčéčüčÅ ą┐ąŠą┐čĆą░ą▓ą║ąŠą╣, ą┐ąŠąĘą▓ąŠą╗čÅčÄčēąĄą╣ čāč湥čüčéčī ą▓ą╗ąĖčÅąĮąĖąĄ ą┐ą╗ą░čüčéąĖč湥čüą║ąĖčģ ą┤ąĄč乊čĆą╝ą░čåąĖą╣. ąĢą│ąŠ ąĘąĮą░č湥ąĮąĖąĄ ą╝ąŠąČąĄčé ą▒čŗčéčī ąŠą┐čĆąĄą┤ąĄą╗ąĄąĮąŠ ą┐ąŠ ą┤ą░ąĮąĮčŗą╝ čéą░ą▒ą╗ąĖčåčŗ ą╗ąĖą▒ąŠ čāčüčéą░ąĮąŠą▓ą╗ąĄąĮąŠ čĆą░ą▓ąĮčŗą╝ ąĄą┤ąĖąĮąĖčåąĄ ą┐čĆąĖ ą┐čĆąŠą▓ąĄą┤ąĄąĮąĖąĖ ą▓ąĄčĆčģąĮąĄą╣ ąŠčåąĄąĮą║ąĖ ą┤ą╗čÅ ąĮąĄąŠą▒čģąŠą┤ąĖą╝ąŠą╣ č鹊ą╗čēąĖąĮčŗ ąøą¤ą×. ąÆ čüą╗čāčćą░ąĄ, ąĄčüą╗ąĖ ą▓ čāčĆą░ą▓ąĮąĄąĮąĖąĖ (24) ą┐čĆąĖąĮčÅčéčī r= b ąĖ Žār = ąĀ ąĖ ą▓čŗą▓ąĄčüčéąĖ ąĖąĘ ą┐ąŠą╗čāčćąĖą▓čłąĄą│ąŠčüčÅ ą▓čŗčĆą░ąČąĄąĮąĖčÅ ą▓ąĄą╗ąĖčćąĖąĮčā ąĢ = b ŌĆō a, ą┐ąŠą╗čāčćąĖčéčüčÅ čüą╗ąĄą┤čāčÄčēą░čÅ č乊čĆą╝čāą╗ą░:
ążąŠčĆą╝čāą╗ą░ (26) čüą┐čĆą░ą▓ąĄą┤ą╗ąĖą▓ą░ ą┤ą╗čÅ ąŠą▒ą╗ą░čüčéąĖ ąøą¤ą×, ą│ą┤ąĄ ą║ą░čüą░č鹥ą╗čīąĮčŗąĄ ąĮą░ą┐čĆčÅąČąĄąĮąĖčÅ ąĮąĖąČąĄ ąĮąŠčĆą╝ą░ą╗čīąĮčŗčģ ą║ąŠą╝ą┐ąŠąĮąĄąĮčé č鹥ąĮąĘąŠčĆą░ ąĮą░ą┐čĆčÅąČąĄąĮąĖą╣, čé.ąĄ. ą▓ąŠ ą▓čüąĄą╝ ąŠą▒čŖąĄą╝ąĄ ąøą¤ą× ąĘą░ ąĖčüą║ą╗čÄč湥ąĮąĖąĄą╝ ąŠą▒ą╗ą░čüčéąĖ ą▓ąĄčĆčģąĮąĄą│ąŠ č鹊čĆčåą░ ąøą¤ą×. ą¤čĆąĖą╝ąĄąĮąĄąĮąĖąĄ čŹč鹊ą╣ č乊čĆą╝čāą╗čŗ ąŠą▒ąŠčüąĮąŠą▓ą░ąĮąŠ č鹊ą╗čīą║ąŠ ą▓ č鹊ą╝ čüą╗čāčćą░ąĄ, ąĄčüą╗ąĖ ąŠą▒ą╗ą░čüčéčī ą▓ąĄčĆčģąĮąĄą│ąŠ č鹊čĆčåą░ ąøą¤ą× ąĮąĄ čÅą▓ą╗čÅąĄčéčüčÅ ąĮą░ąĖą▒ąŠą╗ąĄąĄ ąŠą┐ą░čüąĮąŠą╣ čü č鹊čćą║ąĖ ąĘčĆąĄąĮąĖčÅ ą┐čĆąĄą┤ąĄą╗čīąĮčŗčģ ąĮą░ą┐čĆčÅąČąĄąĮąĖą╣ ą▓ ąĮąĄą┐ąŠą┤ą║čĆąĄą┐ą╗ąĄąĮąĮąŠą╝ čāčćą░čüčéą║ąĄ ąøą¤ą×.
ąŚą░čĆąŠąČą┤ąĄąĮąĖąĄ ąĘąŠąĮčŗ ą┐ą╗ą░čüčéąĖč湥čüą║ąĖčģ ąĮą░ą┐čĆčÅąČąĄąĮąĖą╣ ą▓ ąøą¤ą× čü ąŠą│čĆą░ąĮąĖč湥ąĮąĮąŠą╣ ą▓čŗčüąŠč鹊ą╣ ąĘą░čģąŠą┤ą║ąĖ ą┐čĆąŠąĖčüčģąŠą┤ąĖčé ą▓ ą┐ąĄčĆą▓čāčÄ ąŠč湥čĆąĄą┤čī ąĮą░ ą▓ąĄčĆčģąĮąĄą╝ č鹊čĆčåąĄ ą▓ą▒ą╗ąĖąĘąĖ ą▓ąĮčāčéčĆąĄąĮąĮąĄą╣ ą│čĆą░ąĮąĖčåčŗ ąøą¤ą×, ą┐ąŠčüą║ąŠą╗čīą║čā čĆą░ą┤ąĖą░ą╗čīąĮčŗąĄ ąĮą░ą┐čĆčÅąČąĄąĮąĖčÅ ą▓ čŹč鹊ą╣ ąŠą▒ą╗ą░čüčéąĖ ą╝ąĖąĮąĖą╝ą░ą╗čīąĮčŗ (ąĖąĘ-ąĘą░ čāčüą╗ąŠą▓ąĖčÅ ąŠčéčüčāčéčüčéą▓ąĖčÅ ąĮą░ą│čĆčāąĘą║ąĖ ąĮą░ ą│čĆą░ąĮąĖčåąĄ r = a), ą░ ą▓ąĄčĆčéąĖą║ą░ą╗čīąĮčŗąĄ ą╝ą░ą║čüąĖą╝ą░ą╗čīąĮčŗ ąĖ čüąŠčüčéą░ą▓ą╗čÅčÄčé ą▓ąĄą╗ąĖčćąĖąĮčā ąŠą║ąŠą╗ąŠ q. ą¤čĆąĖ čŹč鹊ą╝ ą▓ ą┤ą░ą╗čīąĮąĄą╣čłąĄą╝ ąĘą░čĆąŠąČą┤ąĄąĮąĖąĄ ąĖ čĆą░ąĘą▓ąĖčéąĖąĄ ąĘąŠąĮčŗ ą┐ą╗ą░čüčéąĖč湥čüą║ąĖčģ ą┤ąĄč乊čĆą╝ą░čåąĖą╣ ą┐čĆąŠąĖčüčģąŠą┤ąĖčé ą▓ ą┐ąŠą╗ąĮąŠą╝ ąŠą▒čŖąĄą╝ąĄ ąøą¤ą×, ą▓ą║ą╗čÄčćą░čÅ čéą░ą║ąČąĄ ąŠą▒ą╗ą░čüčéčī ąĮąĖąČąĮąĄą│ąŠ č鹊čĆčåą░ ąøą¤ą×, ąĖ ąĖą╝ąĄąĮąĮąŠ ą┤ą╗čÅ ąĮąĄąĄ ą▒čāą┤ąĄčé čĆą░ąĮčīčłąĄ ą┤ąŠčüčéąĖą│ąĮčāč鹊 čāčüą╗ąŠą▓ąĖąĄ ą┐čĆąĄą┤ąĄą╗čīąĮąŠą│ąŠ čĆą░ą▓ąĮąŠą▓ąĄčüąĖčÅ ą┐čĆąĖ čĆą░čüą┐čĆąŠčüčéčĆą░ąĮąĄąĮąĖąĖ ąĘąŠąĮčŗ ą┐ą╗ą░čüčéąĖč湥čüą║ąĖčģ ą┤ąĄč乊čĆą╝ą░čåąĖą╣ ą┐ąŠ ą▓čüąĄą╣ č鹊ą╗čēąĖąĮąĄ ąøą¤ą×. ą¤čĆąĖ čŹč鹊ą╝ ą▓ ąŠą▒ą╗ą░čüčéąĖ ą▓ą▒ą╗ąĖąĘąĖ ą▓ąĄčĆčģąĮąĄą│ąŠ č鹊čĆčåą░ ąĖ ą▓ąĮąĄčłąĮąĄą╣ ą│čĆą░ąĮąĖčåčŗ ąøą¤ą× ąĘąŠąĮą░ ą┐ą╗ą░čüčéąĖč湥čüą║ąĖčģ ą┤ąĄč乊čĆą╝ą░čåąĖą╣ ąĮąĄ ą▒čāą┤ąĄčé ą┤ąŠčüčéąĖą│ąĮčāčéą░ ąĖąĘ-ąĘą░ ąŠčüąŠą▒ąĄąĮąĮąŠčüč鹥ą╣ ąĘą░ą┤ą░ąĮąĖčÅ ą│čĆą░ąĮąĖčćąĮčŗčģ čāčüą╗ąŠą▓ąĖą╣, ą║ąŠč鹊čĆčŗąĄ čäą░ą║čéąĖč湥čüą║ąĖ ąŠą┐čĆąĄą┤ąĄą╗čÅčÄčé ą┐ąŠą╗ąĄ ąĮą░ą┐čĆčÅąČąĄąĮąĖą╣: ą║ą░čüą░č鹥ą╗čīąĮčŗąĄ ąĮą░ą┐čĆčÅąČąĄąĮąĖčÅ ąŠą║ą░ąČčāčéčüčÅ ą╝ą░ą╗čŗ, čĆą░ą┤ąĖą░ą╗čīąĮčŗąĄ ąĮą░ą┐čĆčÅąČąĄąĮąĖčÅ ą▒čāą┤čāčé ąĖą╝ąĄčéčī ąĘąĮą░č湥ąĮąĖąĄ ąŠą║ąŠą╗ąŠ ąĀ, ą░ ą▓ąĄčĆčéąĖą║ą░ą╗čīąĮčŗąĄ ŌĆō ąŠą║ąŠą╗ąŠ q. ąĢčüą╗ąĖ ą┐čĆąĖąĮčÅčéčī ą▓ čĆą░čüč湥čé čüąŠąŠčéąĮąŠčłąĄąĮąĖąĄ P ąĖ q, ą║ąŠč鹊čĆąŠąĄ čüą╗ąĄą┤čāąĄčé ąĖąĘ ą║ą╗ą░čüčüąĖč湥čüą║ąŠą╣ č乊čĆą╝čāą╗čŗ ąÉ.ąØ.ąöąĖąĮąĮąĖą║ą░ ą┤ą╗čÅ ą┤ą░ą▓ą╗ąĄąĮąĖčÅ ą▒ąŠą║ąŠą▓ąŠą│ąŠ čĆą░čüą┐ąŠčĆą░ ą┐ąŠčĆąŠą┤ [38], ą░ čéą░ą║ąČąĄ ąĮąĄą║ąŠč鹊čĆąŠą│ąŠ ąĘą░ą┤ą░ąĮąĮąŠą│ąŠ ą│ąĖą┤čĆąŠčüčéą░čéąĖč湥čüą║ąŠą│ąŠ ą┤ą░ą▓ą╗ąĄąĮąĖčÅ čüąŠ čüč鹊čĆąŠąĮčŗ ą┐ąŠą┤ąĘąĄą╝ąĮčŗčģ ą▓ąŠą┤ ą▓ ą┐ąŠčĆąŠą▓ąŠą╝ ą┐čĆąŠčüčéčĆą░ąĮčüčéą▓ąĄ ą┐ąŠčĆąŠą┤,
ą│ą┤ąĄ ╬Į ŌĆō ą║ąŠčŹčäčäąĖčåąĖąĄąĮčé ą¤čāą░čüčüąŠąĮą░ ąĮąĄąĘą░ą╝ąŠčĆąŠąČąĄąĮąĮčŗčģ ą┐ąŠčĆąŠą┤, ąŠą║čĆčāąČą░čÄčēąĖčģ ąøą¤ą×; PhŌĆō ą│ąĖą┤čĆąŠčüčéą░čéąĖč湥čüą║ąŠąĄ ą┤ą░ą▓ą╗ąĄąĮąĖąĄ ą┐ąŠčĆąŠą▓čŗčģ ą▓ąŠą┤, ą¤ą░.
ąĢčüą╗ąĖ ą┐ąŠą┤čüčéą░ą▓ąĖčéčī čāčĆą░ą▓ąĮąĄąĮąĖąĄ (27) ą▓ ą║ą░č湥čüčéą▓ąĄ čéčĆąĄčéčīąĄą│ąŠ ą│ą╗ą░ą▓ąĮąŠą│ąŠ ąĮą░ą┐čĆčÅąČąĄąĮąĖčÅ ą▓ ąĘą░ą║ąŠąĮ ą£ąŠčĆą░ ŌĆō ąÜčāą╗ąŠąĮą░ (23), č鹊 čü čāč湥č鹊ą╝ Žā1 = q ą┐ąŠčüą╗ąĄ ą┐čĆąĄąŠą▒čĆą░ąĘąŠą▓ą░ąĮąĖčÅ ą┐ąŠą╗čāčćąĖčéčüčÅ ąĮąĄčĆą░ą▓ąĄąĮčüčéą▓ąŠ
ąöą╗čÅ čĆą░čüčüą╝ą░čéčĆąĖą▓ą░ąĄą╝čŗčģ čéąĖą┐ąŠą▓ ą┐ąŠčĆąŠą┤ ąĖąĘ čéą░ą▒ą╗ąĖčåčŗ ąĖ ą│ą╗čāą▒ąĖąĮ ąĖčģ ąĘą░ą╗ąĄą│ą░ąĮąĖčÅ ąĮąĄčĆą░ą▓ąĄąĮčüčéą▓ąŠ (28) čüą┐čĆą░ą▓ąĄą┤ą╗ąĖą▓ąŠ ą▓ čłąĖčĆąŠą║ąŠą╝ ą┤ąĖą░ą┐ą░ąĘąŠąĮąĄ ą▓ąŠąĘą╝ąŠąČąĮčŗčģ ąĘąĮą░č湥ąĮąĖą╣ ╬Į 0[0,35; 0,5] ą┤ą░ąČąĄ ą┐čĆąĖ ąĮčāą╗ąĄą▓ąŠą╝ ą┐ą░čĆą░ą╝ąĄčéčĆąĄ Ph.
ą¤čĆąĖ ą▒ąŠą╗čīčłąĖčģ ąĘąĮą░č湥ąĮąĖčÅčģ ą▓čŗčüąŠčéčŗ ąĘą░čģąŠą┤ą║ąĖ h č乊čĆą╝čāą╗ą░ (26) ą┐čĆąĖąĮąĖą╝ą░ąĄčé ą▓ąĖą┤ ą║ą╗ą░čüčüąĖč湥čüą║ąŠą╣ č乊čĆą╝čāą╗čŗ (1), ą┐ąŠčŹč鹊ą╝čā ą▓ą░ąČąĮčŗą╝ čÅą▓ą╗čÅąĄčéčüčÅ ąŠą┐čĆąĄą┤ąĄą╗ąĄąĮąĖąĄ ą║čĆąĖčéąĖč湥čüą║ąŠą│ąŠ ąĘąĮą░č湥ąĮąĖčÅ h, ą┐čĆąĖ ą║ąŠč鹊čĆąŠą╝ ą┤ąŠą┐ąŠą╗ąĮąĖč鹥ą╗čīąĮąŠąĄ čüą╗ą░ą│ą░ąĄą╝ąŠąĄ (26) čüčéą░ąĮąŠą▓ąĖčéčüčÅ ąĮąĄąĘąĮą░čćąĖč鹥ą╗čīąĮčŗą╝, čé.ąĄ. ą┤ą╗čÅ čĆą░čüč湥čéą░ č鹊ą╗čēąĖąĮčŗ ąøą¤ą× čü ą┐čĆąĄą┤ą┐ąŠą╗ąŠąČąĄąĮąĖąĄą╝ ąŠ ąĮąĄąŠą│čĆą░ąĮąĖč湥ąĮąĮąŠą╣ ą▓čŗčüąŠč鹥 ąĘą░čģąŠą┤ą║ąĖ ą╝ąŠąČąĮąŠ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░čéčī č乊čĆą╝čāą╗čā (1).
ąÆ čĆąĄąĘčāą╗čīčéą░č鹥 čüąĄčĆąĖąĖ čćąĖčüą╗ąĄąĮąĮčŗčģ čĆą░čüč湥č鹊ą▓ ąŠą┐čĆąĄą┤ąĄą╗ąĄąĮčŗ ąĘą░ą▓ąĖčüąĖą╝ąŠčüčéąĖ č鹊ą╗čēąĖąĮčŗ ąøą¤ą× ą┐ąŠ č乊čĆą╝čāą╗ąĄ (26) ąŠčé h ą┤ą╗čÅ č湥čéčŗčĆąĄčģ čĆą░ąĘą╗ąĖčćąĮčŗčģ čéąĖą┐ąŠą▓ ą┐ąŠčĆąŠą┤, ą┐čĆąĖą▓ąĄą┤ąĄąĮąĮčŗčģ ą▓ čéą░ą▒ą╗ąĖčåąĄ. ą¤čĆąĄą┤ą┐ąŠą╗ą░ą│ą░ąĄčéčüčÅ, čćč鹊 ╬Š = 1, ╬Į = 0,35, čćąĖčüą╗ąĄąĮąĮąŠ čĆą░čüčüčćąĖčéą░ąĮąĮčŗąĄ ą║čĆąĖą▓čŗąĄ E(h) ą┐čĆąĄą┤čüčéą░ą▓ą╗ąĄąĮčŗ ąĮą░ čĆąĖčü.7.
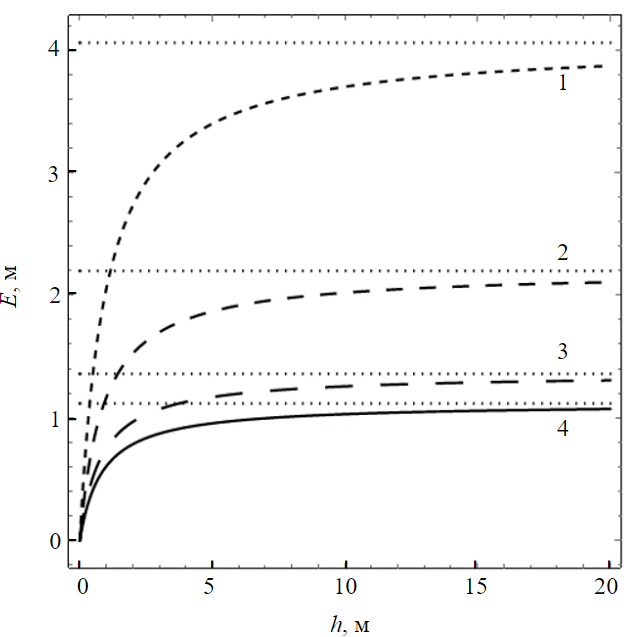
ąĀąĖčü.7. ąŚą░ą▓ąĖčüąĖą╝ąŠčüčéąĖ č鹊ą╗čēąĖąĮčŗ ąĢ ąŠčé ą▓čŗčüąŠčéčŗ ąĘą░čģąŠą┤ą║ąĖ h ą┤ą╗čÅ č湥čéčŗčĆąĄčģ čĆą░čüčüą╝ą░čéčĆąĖą▓ą░ąĄą╝čŗčģ čéąĖą┐ąŠą▓ ą┐ąŠčĆąŠą┤ 1 ŌĆō ą░ą╗ąĄą▓čĆąĖčé; 2 ŌĆō čüčāą┐ąĄčüčī; 3 ŌĆō ą╝ąĄą╗; 4 ŌĆō ą│ą╗ąĖąĮą░
ąØą░ čĆąĖčü.7 č鹊čćą║ą░ą╝ąĖ ąŠą▒ąŠąĘąĮą░č湥ąĮčŗ ą│ąŠčĆąĖąĘąŠąĮčéą░ą╗čīąĮčŗąĄ ą░čüąĖą╝ą┐č鹊čéčŗ, ą║ąŠč鹊čĆčŗąĄ ą┐ąŠą╗čāč湥ąĮčŗ ą▓ čĆąĄąĘčāą╗čīčéą░č鹥 čĆą░čüč湥čéą░ č鹊ą╗čēąĖąĮčŗ ąøą¤ą× ą┐ąŠ č乊čĆą╝čāą╗ąĄ (1), čé.ąĄ. ą▓ čüąĖčéčāą░čåąĖąĖ, ą║ąŠą│ą┤ą░ h ąĮąĄąŠą│čĆą░ąĮąĖč湥ąĮąĮąŠ ą▓ąĄą╗ąĖą║ąŠ. ąÜą░ą║ ą▓ąĖą┤ąĮąŠ ąĖąĘ čĆąĖčü.7, čāąČąĄ ą┐čĆąĖ ą▓čŗčüąŠč鹥 ąĘą░čģąŠą┤ą║ąĖ 9 ą╝ čĆą░ąĘą╗ąĖčćąĖčÅ ą╝ąĄąČą┤čā č乊čĆą╝čāą╗ą░ą╝ąĖ (1) ąĖ (26) čüąŠčüčéą░ą▓ą╗čÅčÄčé ą╝ąĄąĮąĄąĄ 10 %. ą¤čĆąĖ ą▓čŗčüąŠč鹥 ąĘą░čģąŠą┤ą║ąĖ 4 ą╝ čŹčéąĖ čĆą░ąĘą╗ąĖčćąĖčÅ ą╗ąĄąČą░čé ą▓ ą┤ąĖą░ą┐ą░ąĘąŠąĮąĄ ąŠčé 16 ą┤ąŠ 20 %.
ąĪčģąŠąČąĖą╣ ą┐ąŠ ą╝ąĄč鹊ą┤ąŠą╗ąŠą│ąĖąĖ ą░ąĮą░ą╗ąĖąĘ ą▒čŗą╗ ą┐čĆąŠą▓ąĄą┤ąĄąĮ ą▓ čĆą░ą▒ąŠč鹥 [8], ą│ą┤ąĄ čĆą░čüčüą╝ą░čéčĆąĖą▓ą░ą╗čüčÅ čüą╗čāčćą░ą╣ ąŠą┐čĆąĄą┤ąĄą╗ąĄąĮąĖčÅ ua ą▓ ą▓čŗčĆą░ąČąĄąĮąĖąĖ (22) ąĮąĄ ąĮą░ ąŠčüąĮąŠą▓ąĄ čĆąĄčłąĄąĮąĖčÅ čāą┐čĆčāą│ąŠą╣ ąĘą░ą┤ą░čćąĖ (15), ą░ ąĖčüčģąŠą┤čÅ ąĖąĘ ą┐čĆąĄą┤ąĄą╗čīąĮąŠ ą┤ąŠą┐čāčüčéąĖą╝čŗčģ čüą╝ąĄčēąĄąĮąĖą╣ ą▓ąĮčāčéčĆąĄąĮąĮąĄą╣ čüč鹥ąĮą║ąĖ ąøą¤ą×, čćč鹊 ą┐čĆąĖą▓ąĄą╗ąŠ ą║ ą║čĆąĖčéąĖč湥čüą║ąĖą╝ ąĘąĮą░č湥ąĮąĖčÅą╝ ą▓čŗčüąŠčéčŗ ąĘą░čģąŠą┤ą║ąĖ, ą▓ ąĮąĄčüą║ąŠą╗čīą║ąŠ čĆą░ąĘ ą┐čĆąĄą▓čŗčłą░čÄčēąĖą╝ čĆąĄąĘčāą╗čīčéą░čéčŗ ą┤ą░ąĮąĮąŠą│ąŠ ąĖčüčüą╗ąĄą┤ąŠą▓ą░ąĮąĖčÅ. ąóą░ą║ąĖą╝ ąŠą▒čĆą░ąĘąŠą╝, ą┐čĆąĄą┤ą╗ąŠąČąĄąĮąĮčŗą╣ ą┐ąŠą┤čģąŠą┤ ą╝ąŠąČąĄčé čĆą░čüčüą╝ą░čéčĆąĖą▓ą░čéčīčüčÅ ą║ą░ą║ čāč鹊čćąĮąĄąĮąĖąĄ ą┐čĆąĄą┤čŗą┤čāčēąĖčģ ąĖčüčüą╗ąĄą┤ąŠą▓ą░ąĮąĖą╣.
ą×čüąŠą▒ąĄąĮąĮąŠčüčéčī ą┐čĆąĄą┤ą╗ąŠąČąĄąĮąĮąŠą╣ č乊čĆą╝čāą╗čŗ (26) ą┤ą╗čÅ čĆą░čüč湥čéą░ čéčĆąĄą▒čāąĄą╝ąŠą╣ č鹊ą╗čēąĖąĮčŗ ąøą¤ą× čüą▓čÅąĘą░ąĮą░ čü č鹥ą╝, čćč鹊 ą┐čĆąĖ čüčéčĆąĄą╝ą╗ąĄąĮąĖąĖ h ą║ ą▒ąĄčüą║ąŠąĮąĄčćąĮąŠčüčéąĖ č鹊ą╗čēąĖąĮą░ ąøą¤ą× ą▓ č乊čĆą╝čāą╗ąĄ (26) ąĖą╝ąĄąĄčé ą░čüąĖą╝ą┐č鹊čéčā, ą▓ č鹊 ą▓čĆąĄą╝čÅ ą║ą░ą║ ą▓ ą║ą╗ą░čüčüąĖč湥čüą║ąĖčģ č乊čĆą╝čāą╗ą░čģ ąĪ.ąĪ.ąÆčÅą╗ąŠą▓ą░ ą┤ą╗čÅ č鹊ą╗čēąĖąĮ ą╗ąĄą┤ąŠą┐ąŠčĆąŠą┤ąĮąŠą│ąŠ čåąĖą╗ąĖąĮą┤čĆą░ ą┐ąŠ ą║čĆąĖč鹥čĆąĖčÅą╝ ą┐čĆąĄą┤ąĄą╗čīąĮčŗčģ ąĮą░ą┐čĆčÅąČąĄąĮąĖą╣ (3), ą░ čéą░ą║ąČąĄ ą┐čĆąĄą┤ąĄą╗čīąĮčŗčģ ą┤ąĄč乊čĆą╝ą░čåąĖą╣ [20, 27] ąŠčéčüčāčéčüčéą▓čāąĄčé čéą░ą║ąŠąĄ ą░čüąĖą╝ą┐č鹊čéąĖč湥čüą║ąŠąĄ ą┐ąŠą▓ąĄą┤ąĄąĮąĖąĄ, ą░ čüą░ą╝ą░ č鹊ą╗čēąĖąĮą░ čüčéčĆąĄą╝ąĖčéčüčÅ ą║ ą▒ąĄčüą║ąŠąĮąĄčćąĮąŠčüčéąĖ ą┐čĆąĖ hŌåÆ+Ōł×. ąŚą┤ąĄčüčī ąĮąĄčé ą┐čĆąŠčéąĖą▓ąŠčĆąĄčćąĖčÅ, ą┐ąŠčüą║ąŠą╗čīą║čā č乊čĆą╝čāą╗ą░ ąĪ.ąĪ.ąÆčÅą╗ąŠą▓ą░ ą┤ą╗čÅ č鹊ą╗čēąĖąĮčŗ ąøą¤ą× ą┐ąŠ ą║čĆąĖč鹥čĆąĖčÄ ą┐čĆąĄą┤ąĄą╗čīąĮčŗčģ ą┤ąĄč乊čĆą╝ą░čåąĖą╣ ą▓čŗą▓ąŠą┤ąĖą╗ą░čüčī ą┤ą╗čÅ ą╝ą░ą╗čŗčģ ą▓čŗčüąŠčé ąĘą░čģąŠą┤ą║ąĖ ąĖ ąĮąĄ ą┐čĆąĖą╝ąĄąĮąĖą╝ą░ ą┤ą╗čÅ čüą╗čāčćą░čÅ ą▒ąŠą╗čīčłąĖčģ ą▓čŗčüąŠčé ąĘą░čģąŠą┤ą║ąĖ, čćč鹊 čüą╗ąĄą┤čāąĄčé ą║ą░ą║ ąĖąĘ ą░ąĮą░ą╗ąĖąĘą░, ą┐čĆąŠą▓ąĄą┤ąĄąĮąĮąŠą│ąŠ ą▓ čüčéą░čéčīąĄ [20], čéą░ą║ ąĖ ąĖąĘ ą┤ąŠą┐čāčēąĄąĮąĖą╣, ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĮčŗčģ ą▓ čĆą░ą▒ąŠč鹥 [27] ą┐čĆąĖ ą▓čŗą▓ąŠą┤ąĄ ą║ą╗ą░čüčüąĖč湥čüą║ąŠą╣ č乊čĆą╝čāą╗čŗ. ąĪčāčēąĄčüčéą▓ąŠą▓ą░ąĮąĖąĄ ą░čüąĖą╝ą┐č鹊čéčŗ ą┐čĆąĖ čüčéčĆąĄą╝ą╗ąĄąĮąĖąĖ h ą║ ą▒ąĄčüą║ąŠąĮąĄčćąĮąŠčüčéąĖ ą╗ąŠą│ąĖčćąĮąŠ ą┐čĆąĖ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĖ ą┤ąŠą┐čāčēąĄąĮąĖčÅ ąŠ ą┐čĆąĄą┤ąĄą╗čīąĮąŠą╝ čĆą░ą▓ąĮąŠą▓ąĄčüąĮąŠą╝ čüąŠčüč鹊čÅąĮąĖąĖ ą║ąŠąĮčüčéčĆčāą║čåąĖąĖ ąĖ ąĘą░ą╝ąŠčĆąŠąČąĄąĮąĮčŗčģ ą┐ąŠčĆąŠą┤, ą║ą░ą║ ą▓ ą┤ą░ąĮąĮąŠą╣ čĆą░ą▒ąŠč鹥. ąŁč鹊ą│ąŠ ąĮąĄ ą┤ąĄą╗ą░ą╗ąŠčüčī ą┐čĆąĖ ą▓čŗą▓ąŠą┤ąĄ č乊čĆą╝čāą╗čŗ ą┤ą╗čÅ čĆą░čüč湥čéą░ ą╝ąĖąĮąĖą╝ą░ą╗čīąĮąŠą╣ č鹊ą╗čēąĖąĮčŗ ąøą¤ą× ą┐ąŠ ą║čĆąĖč鹥čĆąĖčÄ ą┐čĆąĄą┤ąĄą╗čīąĮčŗčģ ą┤ąĄč乊čĆą╝ą░čåąĖą╣ ą▓ čĆą░ą▒ąŠč鹥 [27].
ą¤čĆąĄą┤čüčéą░ą▓ą╗čÅąĄčé ąĖąĮč鹥čĆąĄčü čĆą░čüčüą╝ąŠčéčĆąĄąĮąĖąĄ ą┤čĆčāą│ąŠą│ąŠ ą┐čĆąĄą┤ąĄą╗čīąĮąŠą│ąŠ čüą╗čāčćą░čÅ ŌĆō ą║ąŠą│ą┤ą░ h čüčéčĆąĄą╝ąĖčéčüčÅ ą║ ąĮčāą╗čÄ. ąÆ čāčüą╗ąŠą▓ąĖčÅčģ ą╝ą░ą╗čŗčģ h ą┐čĆąĄą┤ą╗ąŠąČąĄąĮąĮčāčÄ č乊čĆą╝čāą╗čā (26) ą╝ąŠąČąĮąŠ ą┐čĆąĄą┤čüčéą░ą▓ąĖčéčī ą▓ ą▓ąĖą┤ąĄ ą╗ąĖąĮąĄą╣ąĮąŠą╣ čäčāąĮą║čåąĖąĖ ąŠčé h. ąöą╗čÅ čŹč鹊ą│ąŠ ąĮąĄąŠą▒čģąŠą┤ąĖą╝ąŠ čĆą░ąĘą╗ąŠąČąĖčéčī č乊čĆą╝čāą╗čā (26) ą▓ čĆčÅą┤ ąóąĄą╣ą╗ąŠčĆą░ ą▓ ąŠą║čĆąĄčüčéąĮąŠčüčéąĖ h = 0 čü čüąŠčģčĆą░ąĮąĄąĮąĖąĄą╝ čćą╗ąĄąĮąŠą▓ ą┤ąŠ ą╗ąĖąĮąĄą╣ąĮąŠą│ąŠ ą▓ą║ą╗čÄčćąĖč鹥ą╗čīąĮąŠ:
ąÆčŗčĆą░ąČąĄąĮąĖąĄ (29) ą┤ą░ąĄčé ą║ą░č湥čüčéą▓ąĄąĮąĮąŠ ąŠą┤ąĖąĮą░ą║ąŠą▓čāčÄ ąĘą░ą▓ąĖčüąĖą╝ąŠčüčéčī E = f (P, h) ąŠčé ąŠčüąĮąŠą▓ąĮčŗčģ ą┐ą░čĆą░ą╝ąĄčéčĆąŠą▓ ąĘą░ą┤ą░čćąĖ, ąŠą┤ąĮą░ą║ąŠ ąĖą╝ąĄąĄčéčüčÅ ą╝ąĮąŠąČąĄčüčéą▓ąŠ ąŠčéą╗ąĖčćąĖą╣ ą▓ ą┤ąĄčéą░ą╗čÅčģ. ąĢčüą╗ąĖ ą┤ąŠą┐čāčüčéąĖčéčī, čćč鹊 č乊čĆą╝čāą╗ą░ (3) ą┐čĆąĄą┤čüčéą░ą▓ąĖčé ą║ąŠčĆčĆąĄą║čéąĮčŗą╣ ą┐čĆąŠą│ąĮąŠąĘ ą┐ąŠ č鹊ą╗čēąĖąĮą░ą╝ ąøą¤ą× ą┐čĆąĖ ą╝ą░ą╗čŗčģ h, č鹊 ą┐čĆąĖ ą┐ąŠą╝ąŠčēąĖ čāčĆą░ą▓ąĮąĄąĮąĖčÅ (29) ą╝ąŠąČąĮąŠ ąŠą┐čĆąĄą┤ąĄą╗ąĖčéčī ą║ąŠčŹčäčäąĖčåąĖąĄąĮčé ╬Š čéą░ą║ąĖą╝ ąŠą▒čĆą░ąĘąŠą╝, čćč鹊ą▒čŗ ą▓čŗą┐ąŠą╗ąĮčÅą╗ąŠčüčī čĆą░ą▓ąĄąĮčüčéą▓ąŠ č鹊ą╗čēąĖąĮ ąøą¤ą×, čĆą░čüčüčćąĖčéą░ąĮąĮčŗčģ ą┐ąŠ č乊čĆą╝čāą╗ą░ą╝ (29) ąĖ (3). ąÆ čĆąĄąĘčāą╗čīčéą░č鹥 ą▓čŗą▓ąŠą┤čÅčéčüčÅ ą▓čŗčĆą░ąČąĄąĮąĖčÅ:
ą¤ąŠą╗čāč湥ąĮąĮą░čÅ č乊čĆą╝čāą╗ą░ (30) ą┤ą╗čÅ čĆą░čüč湥čéą░ č鹊ą╗čēąĖąĮčŗ ąøą¤ą× ą▓čŗą▓ąĄą┤ąĄąĮą░ čü čāč湥č鹊ą╝ ╬øŌĆŠ = 2Ctan(ŽĆ/4 + Žå/2) = ŽāčüąČ [24]. ą×ąĮą░ čģąŠčĆąŠčłąŠ čüąŠą│ą╗ą░čüčāąĄčéčüčÅ čü č乊čĆą╝čāą╗ą░ą╝ąĖ (1) ąĖ (3) ąĪ.ąĪ.ąÆčÅą╗ąŠą▓ą░ ą┤ą╗čÅ ąŠą▒ąŠąĖčģ ą┐čĆąĄą┤ąĄą╗čīąĮčŗčģ čüą╗čāčćą░ąĄą▓ ą┐ąŠ ą▓čŗčüąŠč鹥 ąĘą░čģąŠą┤ą║ąĖ. ą¤ąŠą╝ąĖą╝ąŠ čŹč鹊ą│ąŠ, ą┐čĆąĄąĖą╝čāčēąĄčüčéą▓ąŠą╝ č乊čĆą╝čāą╗čŗ (30) ą┐ąŠ čüčĆą░ą▓ąĮąĄąĮąĖčÄ čü čāčĆą░ą▓ąĮąĄąĮąĖąĄą╝ (26) čÅą▓ą╗čÅąĄčéčüčÅ ąŠčéčüčāčéčüčéą▓ąĖąĄ ą┤ąŠą┐ąŠą╗ąĮąĖč鹥ą╗čīąĮčŗčģ ą║ąŠčŹčäčäąĖčåąĖąĄąĮč鹊ą▓, čģą░čĆą░ą║č鹥čĆąĖąĘčāčÄčēąĖčģ čäąĖąĘąĖą║ąŠ-ą╝ąĄčģą░ąĮąĖč湥čüą║ąĖąĄ čüą▓ąŠą╣čüčéą▓ą░ ąĘą░ą╝ąŠčĆąŠąČąĄąĮąĮčŗčģ ą┐ąŠčĆąŠą┤ ╬Į ąĖ čģą░čĆą░ą║č鹥čĆ ą┐ą╗ą░čüčéąĖč湥čüą║ąĖčģ ą┤ąĄč乊čĆą╝ą░čåąĖą╣ ╬Š. ąÜąŠčŹčäčäąĖčåąĖąĄąĮčé ╬Š ą▓ čĆą░ą▓ąĄąĮčüčéą▓ąĄ (30) ąĖą╝ąĄąĄčé čüčāčēąĄčüčéą▓ąĄąĮąĮąŠ ą▒ąŠą╗ąĄąĄ ą▓čŗčüąŠą║ąŠąĄ ąĘąĮą░č湥ąĮąĖąĄ, č湥ą╝ ą┐ąŠ čĆąĄąĘčāą╗čīčéą░čéą░ą╝ čćąĖčüą╗ąĄąĮąĮčŗčģ čĆą░čüč湥č鹊ą▓ ąĖąĘ čéą░ą▒ą╗ąĖčåčŗ.
ąŚą░ą║ą╗čÄč湥ąĮąĖąĄ
ą×čüąĮąŠą▓ąĮčŗą╝ čĆąĄąĘčāą╗čīčéą░č鹊ą╝ ąĖčüčüą╗ąĄą┤ąŠą▓ą░ąĮąĖčÅ čÅą▓ą╗čÅąĄčéčüčÅ ą┐ąŠą╗čāč湥ąĮąĖąĄ č乊čĆą╝čāą╗čŗ čĆą░čüč湥čéą░ čéčĆąĄą▒čāąĄą╝ąŠą╣ č鹊ą╗čēąĖąĮčŗ ą╗ąĄą┤ąŠą┐ąŠčĆąŠą┤ąĮąŠą│ąŠ ąŠą│čĆą░ąČą┤ąĄąĮąĖčÅ čü čāč湥č鹊ą╝ ą║ąŠąĮąĄčćąĮąŠčüčéąĖ ą▓čŗčüąŠčéčŗ ąĘą░čģąŠą┤ą║ąĖ ąĖ ąŠą▒čēąĄą┐čĆąĖąĮčÅč鹊ą│ąŠ ą║čĆąĖč鹥čĆąĖčÅ ą┐čĆąŠčćąĮąŠčüčéąĖ ą£ąŠčĆą░ ŌĆō ąÜčāą╗ąŠąĮą░ ą┤ą╗čÅ ąĘą░ą╝ąŠčĆąŠąČąĄąĮąĮčŗčģ ą│ąŠčĆąĮčŗčģ ą┐ąŠčĆąŠą┤. ąŻč湥čé ą║ąŠąĮąĄčćąĮąŠčüčéąĖ ą▓čŗčüąŠčéčŗ ąĘą░čģąŠą┤ą║ąĖ ąŠčüąŠą▒ąĄąĮąĮąŠ ą▓ą░ąČąĄąĮ ą▓ čāčüą╗ąŠą▓ąĖčÅčģ čüčéčĆąŠąĖč鹥ą╗čīčüčéą▓ą░ čłą░čģčéąĮčŗčģ čüčéą▓ąŠą╗ąŠą▓ ą║ą░ą╗ąĖą╣ąĮčŗčģ čĆčāą┤ąĮąĖą║ąŠą▓ čü ą┐čĆąĖą╝ąĄąĮąĄąĮąĖąĄą╝ ąĖčüą║čāčüčüčéą▓ąĄąĮąĮąŠą│ąŠ ąĘą░ą╝ąŠčĆą░ąČąĖą▓ą░ąĮąĖčÅ ąĖ čüąŠą▓ą╝ąĄčēąĄąĮąĮąŠą╣ č鹥čģąĮąŠą╗ąŠą│ąĖč湥čüą║ąŠą╣ čüčģąĄą╝čŗ ą┐čĆąŠčģąŠą┤ą║ąĖ ąĖ ą║čĆąĄą┐ą╗ąĄąĮąĖčÅ [39, 40].
ąśčüčģąŠą┤čÅ ąĖąĘ ą┐čĆąŠą▓ąĄą┤ąĄąĮąĮčŗčģ čĆą░ąĮąĄąĄ ąĖčüčüą╗ąĄą┤ąŠą▓ą░ąĮąĖą╣ ąŠ ą▓ą╗ąĖčÅąĮąĖąĖ ąĮą░ą┐čĆčÅąČąĄąĮąĮąŠ-ą┤ąĄč乊čĆą╝ąĖčĆąŠą▓ą░ąĮąĮąŠą│ąŠ čüąŠčüč鹊čÅąĮąĖčÅ ąŠą║čĆčāąČą░čÄčēąĖčģ ą┐ąŠčĆąŠą┤ ąĖ ąĮąĄčĆą░ą▓ąĮąŠą╝ąĄčĆąĮąŠčüčéąĖ ą┐ąŠą╗čÅ č鹥ą╝ą┐ąĄčĆą░čéčāčĆ ąĮą░ čéčĆąĄą▒čāąĄą╝čāčÄ č鹊ą╗čēąĖąĮčā ą╗ąĄą┤ąŠą┐ąŠčĆąŠą┤ąĮąŠą│ąŠ ąŠą│čĆą░ąČą┤ąĄąĮąĖčÅ [13, 14, 28], č乊čĆą╝čāą╗ą░ ą╝ąŠąČąĄčé ą▒čŗčéčī ąŠą▒ąŠą▒čēąĄąĮą░ ą┤ą╗čÅ čāč湥čéą░ čŹčéąĖčģ čäą░ą║č鹊čĆąŠą▓. ąöą░ąĮąĮą░čÅ ąĘą░ą┤ą░čćą░ čÅą▓ą╗čÅąĄčéčüčÅ ą┐čĆąĄą┤ą╝ąĄč鹊ą╝ ą┤ą░ą╗čīąĮąĄą╣čłąĖčģ ąĖčüčüą╗ąĄą┤ąŠą▓ą░ąĮąĖą╣ ą░ą▓č鹊čĆąŠą▓.
ą¤čĆąŠčćąĮąŠčüčéąĮąŠą╣ čäą░ą║č鹊čĆ ąĘą░ą╝ąŠčĆąŠąČąĄąĮąĮčŗčģ ą┐ąŠčĆąŠą┤, čĆą░čüčüą╝ąŠčéčĆąĄąĮąĮčŗą╣ ą▓ čüčéą░čéčīąĄ, čćą░čēąĄ ą▓čüąĄą│ąŠ čÅą▓ą╗čÅąĄčéčüčÅ ąŠą┐čĆąĄą┤ąĄą╗čÅčÄčēąĖą╝ ą┤ą╗čÅ ąŠčéąĮąŠčüąĖč鹥ą╗čīąĮąŠ ąĮąĄą│ą╗čāą▒ąŠą║ąŠ ąĘą░ą╗ąĄą│ą░čÄčēąĖčģ čüą╗ąŠąĄą▓ ą┐ąŠčĆąŠą┤ (ą┤ąŠ ą│ą╗čāą▒ąĖąĮčŗ 100-150 ą╝). ą¤čĆąĖ čŹč鹊ą╝ ą┤ą╗čÅ ą▒ąŠą╗ąĄąĄ ą│ą╗čāą▒ąŠą║ąĖčģ čüą╗ąŠąĄą▓ ą┐ąŠčĆąŠą┤ ą┐ąŠą╝ąĖą╝ąŠ čāčüą╗ąŠą▓ąĖčÅ ą┐čĆąŠčćąĮąŠčüčéąĖ ąĘą░ą╝ąŠčĆąŠąČąĄąĮąĮčŗčģ ą│ąŠčĆąĮčŗčģ ą┐ąŠčĆąŠą┤ ą▓ą░ąČąĮąŠ čāčćąĖčéčŗą▓ą░čéčī čäą░ą║č鹊čĆ ą┐ąŠą╗ąĘčāč湥čüčéąĖ ąĖ ąĖčüčüą╗ąĄą┤ąŠą▓ą░čéčī ą┐čĆąĄą┤ąĄą╗čīąĮąŠąĄ ą┤ąĄč乊čĆą╝ąĖčĆąŠą▓ą░ąĮąĮąŠąĄ čüąŠčüč鹊čÅąĮąĖąĄ ą┐ąŠčĆąŠą┤. ą¤ąŠčŹč鹊ą╝čā čüčéą░čéąĖč湥čüą║ąĖą╣ (ą│ąĄąŠą╝ąĄčģą░ąĮąĖč湥čüą║ąĖą╣) čĆą░čüč湥čé čéą░ą║ąČąĄ ą┤ąŠą╗ąČąĄąĮ ą▓ą║ą╗čÄčćą░čéčī ą▓ čüąĄą▒čÅ čĆą░čüč湥čé č鹊ą╗čēąĖąĮčŗ ą╗ąĄą┤ąŠą┐ąŠčĆąŠą┤ąĮąŠą│ąŠ čåąĖą╗ąĖąĮą┤čĆą░ ą┐ąŠ ą║čĆąĖč鹥čĆąĖčÄ ą┐ąŠą╗ąĘčāč湥čüčéąĖ, ąĮą░ą┐čĆąĖą╝ąĄčĆ ą▓ čüąŠąŠčéą▓ąĄčéčüčéą▓ąĖąĖ čü ą╝ąĄč鹊ą┤ąĖą║ąŠą╣ ąĖ č乊čĆą╝čāą╗ą░ą╝ąĖ, ąŠą┐ąĖčüą░ąĮąĮčŗą╝ąĖ ą▓ čĆą░ą▒ąŠč鹥 [27].
ąøąĖč鹥čĆą░čéčāčĆą░
- ą©čāą┐ą╗ąĖą║ ą£.ąØ. ąÉąĮą░ą╗ąĖąĘ čüą┐ąĄčåąĖą░ą╗čīąĮčŗčģ čüą┐ąŠčüąŠą▒ąŠą▓ čüčéčĆąŠąĖč鹥ą╗čīčüčéą▓ą░ ą┐ąŠą┤ąĘąĄą╝ąĮčŗčģ čüąŠąŠčĆčāąČąĄąĮąĖą╣ ą▓ ą│ąŠčĆąŠą┤čüą║ąĖčģ čāčüą╗ąŠą▓ąĖčÅčģ // ąōąŠčĆąĮčŗą╣ ąĖąĮč乊čĆą╝ą░čåąĖąŠąĮąĮąŠ-ą░ąĮą░ą╗ąĖčéąĖč湥čüą║ąĖą╣ ą▒čÄą╗ą╗ąĄč鹥ąĮčī. 2014. Ōä¢ S1. ąĪ. 523-546.
- Ehringhausen N., Schweppe G., te Kamp L., Akinshin I. Numerical Simulation of Shaft Sinking Using the Artificial Freezing Method // Mining Report. 2021. Vol. 157. Iss. 4. P. 350-359.
- ąæą░čĆčÅčģ ąÉ.ąÉ., ąĢą▓čüąĄąĄą▓ ąÉ.ąÆ. ąøąĖą║ą▓ąĖą┤ą░čåąĖčÅ ą║ą░ą╗ąĖą╣ąĮčŗčģ čĆčāą┤ąĮąĖą║ąŠą▓ ąĖ čüąŠą╗čÅąĮčŗčģ čłą░čģčé: ąŠą▒ąĘąŠčĆ ąĖ ą░ąĮą░ą╗ąĖąĘ ą┐čĆąŠą▒ą╗ąĄą╝čŗ // ąōąŠčĆąĮčŗą╣ ąĖąĮč乊čĆą╝ą░čåąĖąŠąĮąĮąŠ-ą░ąĮą░ą╗ąĖčéąĖč湥čüą║ąĖą╣ ą▒čÄą╗ą╗ąĄč鹥ąĮčī. 2019. Ōä¢ 9. ąĪ. 5-29. DOI: 10.25018/0236-1493-2019-09-0-5-29
- ą×ą╗čīčģąŠą▓ąĖą║ąŠą▓ ą«.ą¤. ąÜčĆąĄą┐čī ą║ą░ą┐ąĖčéą░ą╗čīąĮčŗčģ ą▓čŗčĆą░ą▒ąŠč鹊ą║ ą║ą░ą╗ąĖą╣ąĮčŗčģ ąĖ čüąŠą╗čÅąĮčŗčģ čĆčāą┤ąĮąĖą║ąŠą▓. ą£.: ąØąĄą┤čĆą░, 1984. 238 čü.
- ąĪąĄą╝ąĖąĮ ą£.ąÉ., ąæčĆąŠą▓ą║ą░ ąō.ą¤., ą¤čāą│ąĖąĮ ąÉ.ąÆ. ąĖ ą┤čĆ. ąśčüčüą╗ąĄą┤ąŠą▓ą░ąĮąĖąĄ ą▓ą╗ąĖčÅąĮąĖčÅ ąĮąĄąŠą┤ąĮąŠčĆąŠą┤ąĮąŠčüčéąĖ ą┐ąŠą╗čÅ č鹥ą╝ą┐ąĄčĆą░čéčāčĆ ąĮą░ ą┐čĆąŠčćąĮąŠčüčéčī ą╗ąĄą┤ąŠą┐ąŠčĆąŠą┤ąĮčŗčģ ąŠą│čĆą░ąČą┤ąĄąĮąĖą╣ čüčéą▓ąŠą╗ąŠą▓ čłą░čģčé // ąōąŠčĆąĮčŗą╣ ąĖąĮč乊čĆą╝ą░čåąĖąŠąĮąĮąŠ-ą░ąĮą░ą╗ąĖčéąĖč湥čüą║ąĖą╣ ą▒čÄą╗ą╗ąĄč鹥ąĮčī. 2021. Ōä¢ 9. ąĪ. 79-93. DOI: 10.25018/0236_1493_2021_9_0_79
- ąÜą░ąĘąĖą║ą░ąĄą▓ ąö.ą£., ąĪąĄčĆą│ąĄąĄą▓ ąĪ.ąÆ. ąöąĖą░ą│ąĮąŠčüčéąĖą║ą░ ąĖ ą╝ąŠąĮąĖč鹊čĆąĖąĮą│ ąĮą░ą┐čĆčÅąČąĄąĮąĮąŠą│ąŠ čüąŠčüč鹊čÅąĮąĖčÅ ą║čĆąĄą┐ąĖ ą▓ąĄčĆčéąĖą║ą░ą╗čīąĮčŗčģ čüčéą▓ąŠą╗ąŠą▓. ą£.: ąōąŠčĆąĮą░čÅ ą║ąĮąĖą│ą░, 2011. 244 čü.
- Song Zhang, Zurun Yue, Xiangzhong Lu et al. Model test and numerical simulation of foundation pit constructions using the combined artificial ground freezing method // Cold Regions Science and Technology. 2023. Vol. 205. Ōä¢ 103700. DOI: 10.1016/j.coldregions.2022.103700
- ąĪąĄą╝ąĖąĮ ą£.ąÉ., ąøąĄą▓ąĖąĮ ąø.ą«. ą£ąĄč鹊ą┤čŗ čĆą░čüč湥čéą░ ąĖčüą║čāčüčüčéą▓ąĄąĮąĮąŠą│ąŠ ąĘą░ą╝ąŠčĆą░ąČąĖą▓ą░ąĮąĖčÅ ą┐ąŠčĆąŠą┤ ą┐čĆąĖ čüčéčĆąŠąĖč鹥ą╗čīčüčéą▓ąĄ čłą░čģčéąĮčŗčģ čüčéą▓ąŠą╗ąŠą▓. ą£.: ąØą░čāčćąĮčŗą╣ ą╝ąĖčĆ, 2021. 152 čü.
- ąÜąŠą▓čĆąĖąČąĮčŗčģ ąÉ.ą£., ąŻčüąŠą╗čīčåąĄą▓ą░ ą×.ą£., ąÜąŠą▓čĆąĖąČąĮčŗčģ ąĪ.ąÉ. ąĖ ą┤čĆ. ąśčüčüą╗ąĄą┤ąŠą▓ą░ąĮąĖąĄ ą┐čĆąŠčćąĮąŠčüčéąĖ ą░ąĮąĖąĘąŠčéčĆąŠą┐ąĮčŗčģ ą│ąŠčĆąĮčŗčģ ą┐ąŠčĆąŠą┤ ą▓ čāčüą╗ąŠą▓ąĖčÅčģ ąŠčüąĄą▓ąŠą│ąŠ čüąČą░čéąĖčÅ čü ą▒ąŠą║ąŠą▓čŗą╝ ą┤ą░ą▓ą╗ąĄąĮąĖąĄą╝ // ążąĖąĘąĖą║ąŠ-č鹥čģąĮąĖč湥čüą║ąĖąĄ ą┐čĆąŠą▒ą╗ąĄą╝čŗ čĆą░ąĘčĆą░ą▒ąŠčéą║ąĖ ą┐ąŠą╗ąĄąĘąĮčŗčģ ąĖčüą║ąŠą┐ą░ąĄą╝čŗčģ. 2017. Ōä¢ 5. ąĪ. 37-43. DOI: 10.15372/FTPRPI20170505
- ąøąĄą▓ąĖąĮ ąø.ą«., ąĪąĄą╝ąĖąĮ ą£.ąÉ., ą¤ą╗ąĄčģąŠą▓ ą×.ąÉ. ąĪčĆą░ą▓ąĮąĖč鹥ą╗čīąĮčŗą╣ ą░ąĮą░ą╗ąĖąĘ čüčāčēąĄčüčéą▓čāčÄčēąĖčģ ą╝ąĄč鹊ą┤ąŠą▓ čĆą░čüč湥čéą░ č鹊ą╗čēąĖąĮčŗ ą╗ąĄą┤ąŠą┐ąŠčĆąŠą┤ąĮąŠą│ąŠ ąŠą│čĆą░ąČą┤ąĄąĮąĖčÅ čüčéčĆąŠčÅčēąĖčģčüčÅ čłą░čģčéąĮčŗčģ čüčéą▓ąŠą╗ąŠą▓ // ąÆąĄčüčéąĮąĖą║ ą¤ąØąśą¤ąŻ. ąĪčéčĆąŠąĖč鹥ą╗čīčüčéą▓ąŠ ąĖ ą░čĆčģąĖč鹥ą║čéčāčĆą░. 2018. ąó. 9. Ōä¢. 4. ąĪ. 93-103. DOI: 10.15593/2224-9826/2018.4.09
- Chenchen Hu, Zhijiang Yang, Tao Han, Weihao Yang. Calculation Method of the Design Thickness of a Frozen Wall with Its Inner Edge Radially Incompletely Unloaded // Applied Sciences. 2023. Vol. 13. Iss. 23. Ōä¢ 12650. DOI: 10.3390/app132312650
- Sanger F.J., Sayles F.H. Thermal and rheological computations for artificially frozen ground construction // Engineering Geology. 1979. Vol. 13. Iss. 1-4. P. 311-337. DOI: 10.1016/0013-7952(79)90040-1
- Yang Wei-hao, Du Zi-bo, Yang Zhi-jiang, Bo Dong-liang. Plastic design theory of frozen soil wall based on interaction between frozen soil wall and surrounding rock // Chinese Journal of Geotechnical Engineering. 2013. Vol. 35. Iss. 10. P. 1857-1862.
- Bo Zhang, Weihao Yang, Baosheng Wang. Plastic Design Theory of Frozen Wall Thickness in an Ultradeep Soil Layer Considering Large Deformation Characteristics // Mathematical Problems in Engineering. 2018. Vol. 2018. Ōä¢ 8513413. DOI: 10.1155/2018/8513413
- Akhtar S., Li B. Numerical Analysis of Pipeline Uplift Resistance in Frozen Clay Soil Considering Hybrid Tensile-Shear Yield Behaviors // International Journal of Geosynthetics and Ground Engineering. 2020. Vol. 6. Iss. 4. Ōä¢ 47. DOI: 10.1007/s40891-020-00228-9
- Xingyan Liu, Enlong Liu. Application of new twin-shear unified strength criterion to frozen soil // Cold Regions Science and Technology. 2019. Vol. 167. Ōä¢ 102857. DOI: 10.1016/j.coldregions.2019.102857
- Jilin Qi, Wei Ma. A new criterion for strength of frozen sand under quick triaxial compression considering effect of confining pressure // Acta Geotechnica. 2007. Vol. 2. Iss. 3. P. 221-226. DOI: 10.1007/s11440-007-0034-z
- Pouragha M., Jebeli M., Glade R. Failure of partially saturated frozen soils: A micromechanical analysis // Cold Regions Science and Technology. 2023. Vol. 210. Ōä¢ 103842. DOI: 10.1016/j.coldregions.2023.103842
- Dongwei Li, Xin Yang, Junhao Chen. A study of Triaxial creep test and yield criterion of artificial frozen soil under unloading stress paths // Cold Regions Science and Technology. 2017. Vol. 141. P. 163-170.
- Kostina A., Zhelnin M., Plekhov O. et al. An Applicability of VyalovŌĆÖs equations to ice wall strength estimation // Frattura ed Integrit├Ā Strutturale. 2020. Vol. 14 (53). P. 394-405. DOI: 10.3221/igf-esis.53.30
- Feng Hou, Yuanming Lai, Enlong Liu et al. A creep constitutive model for frozen soils with different contents of coarse grains // Cold Regions Science and Technology. 2018. Vol. 145. P. 119-126. DOI: 10.1016/j.coldregions.2017.10.013
- Li Dong-Wei, Fan Ju-Hong, Wang Ren-He. Research on visco-elastic-plastic creep model of artificially frozen soil under high confining pressures // Cold Regions Science and Technology. 2011. Vol. 65. Iss. 2. P. 219-225. DOI: 10.1016/j.coldregions.2010.08.006
- Nishimura S., Gens A., Oliverlla S., Jardine R.J. THM-coupled finite element analysis of frozen soil: formulation and application // G├®otechnique. 2009. Vol. 59. Iss. 3. P. 159-171. DOI: 10.1680/geot.2009.59.3.159
- Kostina A., Zhelnin M., Plekhov O. et al. Creep behavior of ice-soil retaining structure during shaft sinking // Procedia Structural Integrity. 2018. Vol. 13. P. 1273-1278. DOI: 10.1016/j.prostr.2018.12.260
- Vyalov S.S., Zaretsky Yu.K., Gorodetsky S.E. Stability of Mine Workings in Frozen Soils // Developments in Geotechnical Engineering. 1979. Vol. 26. P. 339-351. DOI: 10.1016/B978-0-444-41782-4.50031-2
- Zhelnin M., Kostina A., Plekhov O. et al. Numerical analysis of application limits of VyalovŌĆÖs formula for an ice-soil wall thickness // Frattura ed Integrit├Ā Strutturale. 2019. Vol. 13 (49). P. 156-166. DOI: 10.3221/IGF-ESIS.49.17
- ąÆčÅą╗ąŠą▓ ąĪ.ąĪ. ą¤čĆąŠčćąĮąŠčüčéčī ąĖ ą┐ąŠą╗ąĘčāč湥čüčéčī ą╝ąĄčƹʹ╗čŗčģ ą│čĆčāąĮč鹊ą▓ ąĖ čĆą░čüč湥čéčŗ ą╗ąĄą┤ąŠą│čĆčāąĮč鹊ą▓čŗčģ ąŠą│čĆą░ąČą┤ąĄąĮąĖą╣. ą£.: ąśąĘą┤-ą▓ąŠ ąÉą║ą░ą┤ąĄą╝ąĖąĖ ąĮą░čāą║ ąĪąĪąĪąĀ, 1962. 254 čü.
- Semin M. Calculation of frozen wall thickness considering the non-uniform distribution of the strength properties // Procedia Structural Integrity. 2021. Vol. 32. P. 180-186. DOI: 10.1016/j.prostr.2021.09.026
- Bekele Y.W., Kyokawa H., Kvarving A.M. et al. Isogeometric analysis of THM coupled processes in ground freezing // Computers and Geotechnics. 2017. Vol. 88. P. 129-145. DOI: 10.1016/j.compgeo.2017.02.020
- Tounsi H., Rouabhi A., Jahangir E. Thermo-hydro-mechanical modeling of artificial ground freezing taking into account the salinity of the saturating fluid // Computers and Geotechnics. 2020. Vol. 119. Ōä¢ 103382. DOI: 10.1016/j.compgeo.2019.103382
- Vallier F., Mitani Y., Boulon M. et al. A Shear Model Accounting Scale Effect in Rock Joints Behavior // Rock Mechanics and Rock Engineering. 2010. Vol. 43. Iss. 5. P. 581-595. DOI: 10.1007/s00603-009-0074-9
- Huabei Liu. Unified sand modeling using associated or non-associated flow rule // Mechanics Research Communications. 2013. Vol. 50. P. 63-70. DOI: 10.1016/j.mechrescom.2013.04.003
- Shi Z., Buscarnera G., Finno R.J. Simulation of cyclic strength degradation of natural clays via bounding surface model with hybrid flow rule // International Journal for Numerical and Analytical Methods in Geomechanics. 2018. Vol. 42. Iss. 14. P. 1719-1740. DOI: 10.1002/nag.2813
- ąÜą░čĆąĄą▓ ąÆ.ąś., ąÜąŠą▓ą░ą╗ąĄąĮą║ąŠ ą«.ąż., ąŻčüčéąĖąĮąŠą▓ ąÜ.ąæ. ą£ąŠą┤ąĄą╗ąĖčĆąŠą▓ą░ąĮąĖąĄ ą┤ąĄč乊čĆą╝ąĖčĆąŠą▓ą░ąĮąĖčÅ ąĖ čĆą░ąĘčĆčāčłąĄąĮąĖčÅ ą░ąĮąĖąĘąŠčéčĆąŠą┐ąĮčŗčģ ą┐ąŠčĆąŠą┤ ą▓ą▒ą╗ąĖąĘąĖ ą│ąŠčĆąĖąĘąŠąĮčéą░ą╗čīąĮąŠą╣ čüą║ą▓ą░ąČąĖąĮčŗ // ążąĖąĘąĖą║ąŠ-č鹥čģąĮąĖč湥čüą║ąĖąĄ ą┐čĆąŠą▒ą╗ąĄą╝čŗ čĆą░ąĘčĆą░ą▒ąŠčéą║ąĖ ą┐ąŠą╗ąĄąĘąĮčŗčģ ąĖčüą║ąŠą┐ą░ąĄą╝čŗčģ. 2017. Ōä¢ 3. ąĪ. 12-21.
- ąæąĄąĘą╝ą░č鹥čĆąĮčŗčģ ąÉ.ąÆ., ą×čäčĆąĖčģč鹥čĆ ąÆ.ąō. ą»ą▓ą╗ąĄąĮąĖąĄ ą┤ąĖą╗ą░čéą░ąĮčüąĖąĖ ąĖ ąĄą│ąŠ ą▓ą╗ąĖčÅąĮąĖąĄ ąĮą░ čģą░čĆą░ą║č鹥čĆ ą┤ąĄč乊čĆą╝ąĖčĆąŠą▓ą░ąĮąĖčÅ ą│čĆčāąĮč鹊ą▓ ą┐ąŠą┤ ąĮą░ą│čĆčāąĘą║ąŠą╣ // MasterŌĆÖs Journal. 2017. Ōä¢ 2. ąĪ. 85-90.
- Junchen Zhou, Keyong Wang, Peichao Li. Hybrid fundamental solution based finite element method for axisymmetric potential problems with arbitrary boundary conditions // Computers & Structures. 2019. Vol. 212. P. 72-85. DOI: 10.1016/j.compstruc.2018.10.012
- ąØą░čüąŠąĮąŠą▓ ąś.ąö., ą©čāą┐ą╗ąĖą║ ą£.ąØ. ąŚą░ą║ąŠąĮąŠą╝ąĄčĆąĮąŠčüčéąĖ č乊čĆą╝ąĖčĆąŠą▓ą░ąĮąĖčÅ ą╗ąĄą┤ąŠą┐ąŠčĆąŠą┤ąĮčŗčģ ąŠą│čĆą░ąČą┤ąĄąĮąĖą╣ ą┐čĆąĖ čüąŠąŠčĆčāąČąĄąĮąĖąĖ čüčéą▓ąŠą╗ąŠą▓ čłą░čģčé. ą£.: ąØąĄą┤čĆą░, 1976. 237 čü.
- ą×ą╗ąŠą▓čÅąĮąĮčŗą╣ ąÉ.ąō. ąæąŠą║ąŠą▓ąŠą╣ čĆą░čüą┐ąŠčĆ ą▓ ą╝ą░čüčüąĖą▓ąĄ ą│ąŠčĆąĮčŗčģ ą┐ąŠčĆąŠą┤ // ąŚą░ą┐ąĖčüą║ąĖ ąōąŠčĆąĮąŠą│ąŠ ąĖąĮčüčéąĖčéčāčéą░. 2010. ąó. 185. ąĪ. 141-147.
- ą£ąĖčłąĄą┤č湥ąĮą║ąŠ ąÉ.ąÉ. ą× ąĮąĄąŠą▒čģąŠą┤ąĖą╝ąŠčüčéąĖ ą┐čĆąĖą╝ąĄąĮąĄąĮąĖčÅ ąĖąĮąĮąŠą▓ą░čåąĖąŠąĮąĮąŠą╣ ą║ąŠąĮčüčéčĆčāą║čåąĖąĖ čćčāą│čāąĮąĮąŠą╣ ą║čĆąĄą┐ąĖ ą┐čĆąĖ čüčéčĆąŠąĖč鹥ą╗čīčüčéą▓ąĄ ą▓ąĄčĆčéąĖą║ą░ą╗čīąĮčŗčģ čłą░čģčéąĮčŗčģ čüčéą▓ąŠą╗ąŠą▓ ą│ą╗čāą▒ąĖąĮąŠą╣ ą▒ąŠą╗ąĄąĄ 500 ą╝ // ą£ą░čĆą║čłąĄą╣ą┤ąĄčĆąĖčÅ ąĖ ąĮąĄą┤čĆąŠą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄ. 2017. Ōä¢ 4 (90). ąĪ. 37-39.
- Semin M., Golovatyi I., Levin L., Pugin A. Enhancing efficiency in the control of artificial ground freezing for shaft construction: A case study of the Darasinsky potash mine // Cleaner Engineering and Technology. 2024. Vol. 18. Ōä¢ 100710. DOI: 10.1016/j.clet.2023.100710
