Методология моделирования нелинейных геомеханических процессов в блочных и слоистых горных массивах на моделях из эквивалентных материалов
Аннотация
Цель исследований – разработка методологии, повышающей достоверность воспроизведения и исследования на моделях из эквивалентных материалов сложных нелинейных процессов деформирования и разрушения структурированных горных массивов под влиянием подземных горных работ для обеспечения более точного прогноза возникновения опасных явлений и оценки их последствий. Разработаны новые подходы к критериям подобия, базирующиеся на основополагающих законах термодинамики; новые типы эквивалентных материалов, удовлетворяющих этим критериям; системы формирования различных начальных и граничных условий, регулируемых с помощью специально разработанных компьютерных программ; новые технические средства более надежного определения напряжений в моделях; новые методы решения обратных геомеханических задач при отсутствии необходимых исходных натурных данных. С использованием разработанной методологии решен ряд сложных нелинейных задач, связанных с оценками колебательного характера изменения опорного давления при динамических процессах обрушения кровли; диапазонов изменения частоты процессов при деформировании и разрушении элементов массива, диапазонов изменения их ускорений; параметров сдвижений с нарушением сплошности массива под влиянием горных работ: секущих трещин, отслоений, зияющих пустот, учет которых необходим для оценки опасности формирования сплошных водопроводящих каналов в водозащитной толще.
Введение
В мировой практике разработки месторождений твердых полезных ископаемых накоплен значительный потенциал управления геомеханическими процессами, т.е. целенаправленного изменения напряженно-деформированного состояния (НДС) массива горных пород с целью обеспечения эффективности и безопасности горного производства. Результаты анализа практического опыта разработки месторождений твердых полезных ископаемых показали, что существует много примеров разрушения горных выработок, снижения безопасности горных работ и экономической эффективности горного производства, увеличения потерь полезного ископаемого, техногенных и экологических катастроф [9, 10, 14].
Возникновение таких аварийных ситуаций предопределено недостаточной полнотой современных научных знаний о физической сущности масштабных нелинейных геомеханических процессов, протекающих в областях массива горных пород, недоступных для прямых измерений при постоянно изменяющихся параметрах техногенных трещин (расслоения, секущих), блочных структур, а также нелинейных параметров сдвижений и горного давления по мере развития подземных горных работ [34]. Существенное влияние на вероятность аварийных ситуаций в последние 20-25 лет оказывают также резкое повышение интенсивности очистных работ, связанное с использованием высокопроизводительного очистного и проходческого оборудования и, как следствие, – качественные изменения геомеханических процессов.
Практический опыт использования различных методов исследований НДС реальных блочных и слоистых горных массивов показывает, что большими потенциальными возможностями для исследования подобных нелинейных процессов в различных горнотехнических ситуациях и получения не только качественных, но и количественных характеристик обладает метод моделирования на моделях из эквивалентных материалов (ЭМ). С использованием данного метода, предложенного Г.Н.Кузнецовым, и получившим практическое воплощение как в его работах, так и в исследованиях М.Ф.Шклярского, М.Н.Будько, М.С.Злотникова Ф.П.Глушихина, А.А.Борисова, В.П.Зубова, был решен ряд задач, имеющих важное научное и практическое значение, установлены основные качественные зависимости параметров НДС горного массива от геологических и горнотехнических факторов. В работах Ф.П.Глушихина, М.В.Курлени, В.Н.Ревы, М.А.Розенбаума, Г.Л.Фисенко, Е.И.Шемякина, М.Ф.Шклярского установлено «явление зональной дезинтеграции горных пород вокруг подземных выработок» [34]. Этот метод, основанный на базе критериев подобия Г.Н.Кузнецова, получил распространение более чем в 30 странах мира: Германии, Китае, Франции и др. В последнее время метод наиболее часто применяется в Китае при решении различных геомеханических задач. Например, решение проблем разработки глубоко залегающих месторождений [24, 29], исследование процессов динамических сдвижений при разработке полезных ископаемых [25, 28, 30], влияния трещиноватости кровли на параметры мульды сдвижений [31-33], дисперсного состава материалов на их деформационные характеристики [26], процессов разрушения целиков [27].
Постановка проблемы
Современный уровень развития метода моделирования на ЭМ не позволяет в полной мере обеспечить раскрытие его потенциальных возможностей для более достоверного воспроизведения и надежного исследования глубинных, сложных динамических процессов трансформации различных структур и физических полей при подземной разработке твердых полезных ископаемых. Многолетние исследования, выполненные во ВНИМИ и Санкт-Петербургском горном университете, показали, что решение этой важной задачи возможно только при разработке новой методологии исследований, базирующейся на более универсальных критериях подобия, разработке соответствующих им типов ЭМ и технических решений, обеспечивающих подобие начальных и граничных условий для моделируемой области массива, воспроизведение различных видов горных работ, а также исследование комплекса физических полей, динамических и энергообменных процессов.
Основы моделирования на ЭМ
Основы современных научных представлений о существовании подобных физических явлений были заложены в середине 19 в. В работах Ж.Бертрана, Рэлея, Т.А.Афанасьевой-Эренфест, Ж.Букингема, А.Федермана были установлены фундаментальные признаки подобия физических явлений, основывающиеся на анализе размерностей, теореме Ньютона о динамическом подобии, связи числа безразмерных комплексов с числом размерных величин их составляющих. Дальнейшее развитие теория подобия получила в работах М.В.Кирпичева, Л.И.Седова, П.К.Кондакова, а применение этой теории применительно к исследованию геомеханических процессов – в работах Г.Н.Кузнецова, А.А.Борисова и других исследователей [8, 23, 34].
Ключевыми элементами теории подобия являются связанные между собой константы подобия, величины которых определяются основными физическими законами. Выведенное еще Ж.Бертраном математическое выражение для инварианта динамического подобия основывалось на общем понятии динамического подобия, высказанном Ньютоном, поэтому это математическое выражение называют обычно «законом подобия Ньютона». В работах Г.Н.Кузнецова приводится математический вывод этого закона [8], основанного на обеспечении геометрического, кинематического и динамического подобия, который в конечной форме может быть выражен в виде уравнения:
где P,t, ρ,l,a – сила, время, плотность, размер элемента, ускорение; м и н– индексы, соответствующие модели и натуре; idem– обозначение числа Ньютона; inv – некоторое безразмерное число (определяющий критерий подобия).
В дальнейшем делается предположение, что «деформации и разрушения породы происходят в результате действия сил тяжести» и вывод, что aм = aн = g = const, после чего для выбора эквивалентных материалов определяется их характеристика N, имеющая размерность «сила, деленная на площадь» [8]. В этом случае:
Данное уравнение и соответствующие ему критерии подобия используются в неизменном виде практически во всех работах при использовании данного метода [2, 18, 23]. На основании этих критериев подбираются типы ЭМ [3, 15, 19], определяются параметры технических устройств и стендов для обеспечения начальных и граничных условий в исследуемой области массива [16, 17]. Из подобранных типов ЭМ изготавливаются модели горных массивов [11, 12], моделируются различные типы горных работ, исследуются процессы деформирования и разрушения горных пород [1, 4, 22], осуществляется взаимное тестирование методов численного и физического моделирования [13, 17].
Разработка новой методологии моделирования на ЭМ
Выведенное Г.Н.Кузнецовым соотношение относится к любому однородному по «плотности» и «изотропности» элементу горного массива в форме куба с размерами, позволяющими считать его квазиоднородным. В отличие от сделанных Г.Н.Кузнецовым предположений будем считать, что в первом приближении основными силами, определяющими геомеханические процессы, являются не только силы тяжести, но и силы реакции или внутренние напряжения в элементе массива, определяемые наличием как гравитационных, так и тектонических сил, под воздействием которых в породах может происходить перераспределение различных видов энергии. От баланса этих видов энергии может существенно зависеть развитие процессов деформирования и разрушения горных пород под действием как природных, так и техногенных факторов.
Для учета всего комплекса этих физических величин была разработана новая методология на базе общего закона сохранения энергии или 1-го закона термодинамики [34]:
где dU – изменение внутренней энергии тела; TdS – внешняя тепловая энергия, SdT – генерирование тепловой энергии системой, например, при окислительных процессах; ∑Xidxi – работа внешних сил; ∑xidXi – работа, совершаемая горным массивом.
Применительно к исследованию геомеханических процессов при отсутствии поступления внешней тепловой энергии для обеспечения их подобия в модели необходимо обеспечить пропорциональность всех основных составляющих энергетического баланса в модели, идентичную натуре при условии наличия некоторого «эталона» энергетической составляющей.
Учитывая, что любой моделируемый элемент и его модель находятся в едином гравитационном поле Земли, за этот эталон может быть принята их потенциальная энергия W = mgh. Определим другие составляющие энергетического баланса: кинетическая Wкин = mν2/2; упругая Wупр = σεV/2; тепловая Wтепл = cmΔT, где m, h, σ, ε, ν, V, c, ΔT – масса, высота, напряжение, относительная деформация, скорость, объем, удельная теплоемкость, изменение температуры. Преобразуем данные выражения в систему уравнений для переходных множителей всех составляющих энергетического баланса (αWi) с учетом переходных множителей αρ, αl, αε, ασ, αE, αΔT, αα αc, (для плотностей, линейных размеров, относительных деформаций, напряжений, модулей деформаций, приращения тепловой энергии, ускорений, удельных теплоемкостей) и перейдем от величин энергий к их удельным составляющим: Wiуд = Wi/V, где индекс i соответствует любой из составляющих энергетического баланса,
Очевидно, что для обеспечения пропорциональности всех составляющих система равенств может быть выполнена, если одновременно будет выполнена новая система равенств:
Для выполнения этой системы необходимо:
Для обеспечения постоянства линейного масштаба моделирования при всех деформациях в модели необходимо, чтобы и приращения линейных размеров были связаны с этим же масштабом αl, что равносильно выполнению требования αε = 1. Тогда αE = αραl; ασ = αεαE = αραl.
Таким образом, пропорциональность первых трех составляющих системы уравнений αWпот = αWкин = αWупр = αραl обеспечивается при условии αE = ασ = αραl.
Пропорциональность четвертой, тепловой составляющей системы уравнений может быть обеспечена при условии αΔT = αl/αc (тогда αWтепл = αραl). Доказательство возможности обеспечения этого условия можно найти в условии обеспечения энергетического баланса при переходе потенциальной энергии W = mgh полностью в тепловую: mgh = cmΔT, а также кинетической – в тепловую: mv2/2 = cmΔT, откуда из любого из уравнений легко определяется αΔT = αl/αc.
Таким образом, для, обеспечения подобия динамических процессов, связанных с преобразованием различных видов энергии, необходимо обеспечить подбор искусственных материалов при одновременном выполнении двух условий: αE = αραl; ασ = αραl. При этом обеспечивается равенство переходных множителей для всех составляющих энергетического баланса:
При единовременном выполнении этих условий все переходные множители для модулей деформаций, напряжений и всех составляющих энергетического баланса принимают одинаковое значение – форму единого условия подобия αi = αραl = const.
Масштаб времени для динамических процессов, протекающих с ускорением α, определяется из уравнения l = αt2/2:αt = (l)0,5. При этом все относительные деформации элементов массива и их ускорения в натуре и модели имеют идентичные значения.
В общем случае необходимо подобие более полных зависимостей:
В частном случае, при учете только сил тяжести критерий подобия принимает известный вид в форме, представленной Г.Н.Кузнецовым: Nм/γмlм = Nн/γнlн = idem.
Разработка новых типов ЭМ и системы формирования граничных условий
С учетом единого условия подобия был проведен сравнительный анализ параметров различных типов горных пород и различных типов ЭМ. Для этого были рассмотрены результаты наиболее распространенных видов испытаний образцов горных пород в условиях одноосного сжатия, а определение их параметров производилось на основе подобия максимально накопленной удельной упругой энергии:
Этот критерий был использован для разработки ЭМ с физико-механическими параметрами, обеспечивающими выполнение условий подобия для самого широкого круга типов горных пород.
В результате проведенного анализа были установлены зависимости максимальной удельной энергии различных типов горных пород и ЭМ от прочности на одноосное сжатие. На рис.1 приведены зависимости Wудм от Rсж, полученные по результатам испытаний, проведенных различными авторами [22], более 500 образцов 20 основных типов горных пород. Величина Wудм рассчитывалась по результатам стандартных программ испытаний [8, 34]:
С учетом критериев подобия идентичные параметры ЭМ были пересчитаны на натурные условия и перенесены на общее поле результатов натурных испытаний. В результате проведенных испытаний более чем 10 типов ЭМ и расчетов были установлены только три типа ЭМ и их параметры, которые в наибольшей степени удовлетворяли критериям подобия, но при этом позволяли воспроизводить практически все типы горных пород. На рис.2 представлены характеристики одного из этих типов пород, позволяющих при варьировании рецептуры адекватно воспроизводить большинство типов горных пород в широком диапазоне масштабов моделирования.
При необходимости более точного воспроизведения динамических процессов и наличии необходимых результатов испытания горных пород требуется воспроизведение всей кривой деформирования в координатах σ-ε в до- и запредельной области.
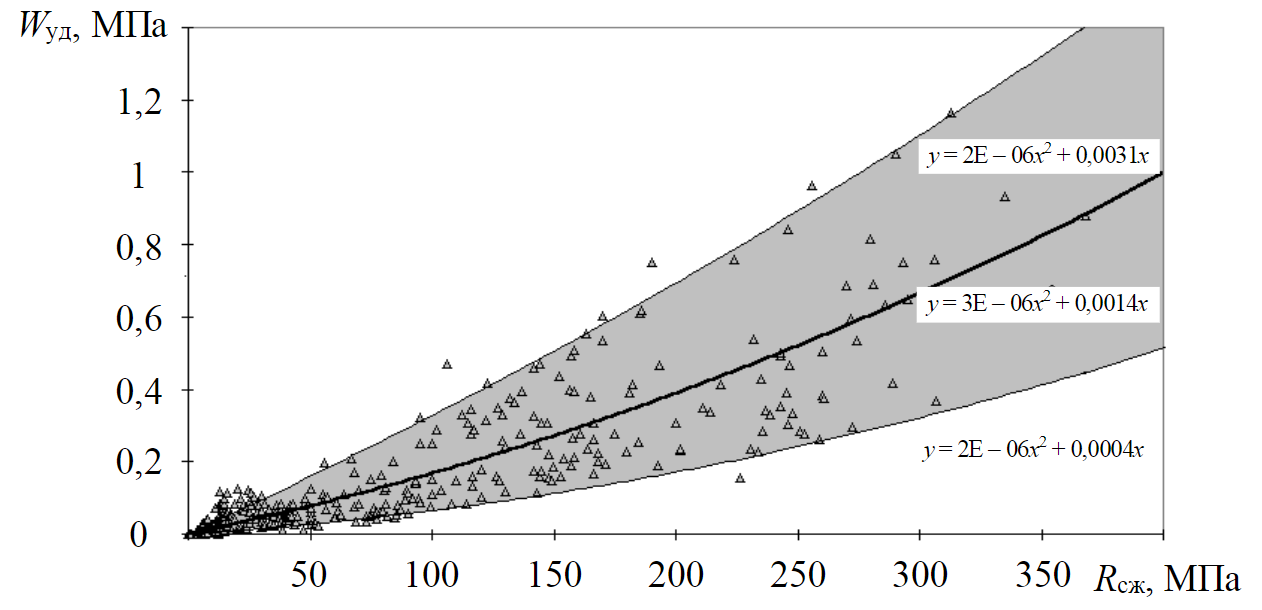
Рис.1. Зависимости Wуд от Rсж для различных типов горных пород
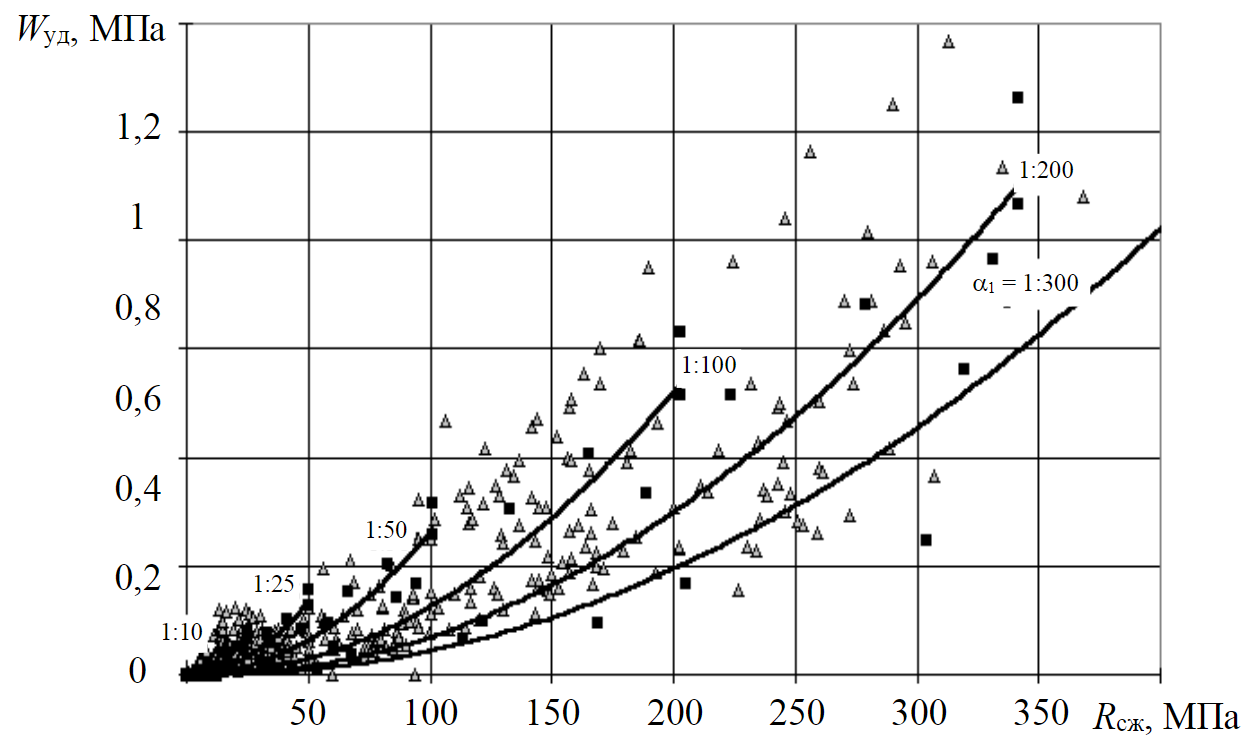
Рис.2. Зависимости Wуд от Rсж для ЭМ на основе смолы ДЭГ-1,пересчитанные на натурные условия
Для расширения диапазона формирования различных граничных условий на границах области моделируемого объекта во ВНИМИ и НЦ Горного университета была разработана, изготовлена и налажена специальная автоматизированная система, представляющая собой комплекс из 32 управляемых силовых нагружающих элементов с суммарным усилием 96 000 Н, позволяющих с помощью специального программного обеспечения формировать на границе модели в общем случае неоднородные эпюры – от режимов заданных нагрузок до режимов заданных деформаций. Результаты проверки показали, что программа и оборудование стендов обеспечивают формирование заданных эпюр в ручном, пошаговом и автоматическом режиме и их поддержание в режиме саморегулирования заданных нагрузок и заданных деформаций в диапазоне масштабов моделирования от 1:20 до 1:1000 практически для всего диапазона моделируемых горных пород.
Методы исследования моделей
Для повышения надежности результатов моделирования и расширения области применения метода ЭМ, помимо обеспечения подобия параметров ЭМ и граничных условий, важным является получение достоверной информации о параметрах различных физических и геофизических полей. Многомерная информация о протекающих в модели процессах может быть использована либо для дешифровки результатов исследований, полученных в натурных условиях, либо для получения новых данных, которые очень сложно или практически невозможно получить в производственных условиях. Среди этих полей можно выделить поля напряжений, деформаций, тепловые поля, акустическую и электромагнитную индукцию, анализ которых позволяет получить более полную информацию о глубинных процессах, протекающих в «теле» модели, которые коррелируют с процессами, протекающими в горных массивах вследствие схожести физической природы горных пород и ЭМ. Очевидно, что необходимыми элементами такой информационно-измерительной системы (ИИС) являются датчики соответствующих физических величин и устройства для их «опроса» и регистрации как в квазистатических, так и динамических режимах.
В состав ИИС вошел целый ряд стандартных датчиков физических величин и систем, удовлетворяющих самым высоким современным требованиям по чувствительности, точности, частотному диапазону, скорости регистрации и т.п. [20], однако для получения важнейшей информации о параметрах напряжений в блочных и слоистых массивах потребовалось разработать специальные, совершенно новые миниатюрные датчики напряжений для их прямого определения в «теле» различных блочных систем, так как существующие крупногабаритные датчики, применяемые для исследования геомеханических задач в моделях из ЭМ, не обеспечивали получение надежной информации или существенно искажали развитие изучаемых процессов.
Для решения этого вопроса были проанализированы результаты теоретических и экспериментальных исследований, полученных Д.С.Барановым, Л.Н.Фомицей, Б.Б.Тимофеевым, Г.В.Рыковым и др. [6, 8] в расширенном списке научных дисциплин за рамками тематики горной геомеханики при определении напряжений в различных типах материалах. В результате была сформирована система неравенств, обеспечивающих определение как статических, так и динамических напряжений, с помощью некоторых универсальных одиночных датчиков во всем диапазоне деформационных параметров дискретных сред (EЭМ = 10-4000 МПа), одним из главных параметров которых является приведенный модуль деформации Eд, при условии минимизации искажений, вносимых датчиком в исследуемое поле напряжений (отношение толщины датчика к его диаметру < 0,1-0,15), максимально возможное удаление места расположения чувствительного элемента от искажающих поле напряжений краев датчика (dчэ/d < 0,6-0,7), но при уменьшении разброса его показаний, обусловленных «зернистостью среды» (dчэ > 10dз). При соблюдении этих ограничений была поставлена задача определения максимально возможной величины Ед, обеспечивающей превышение величины EЭМ, при которой систематическая погрешность измерений не могла превышать 5 %, что обеспечивало возможность применения датчика во всех типах ЭМ.
Для расчета Eд была предложена новая расчетная методика, реализованная на ФОРТРАНЕ на основе усреднения по рабочим поверхностям датчика их относительных деформаций и учитывающая специфику активных, информативных составляющих чувствительных элементов при воздействии конечного распределенного давления р [6, 7].
С учетом рассмотренных ограничений при предварительном выборе материала корпуса датчика из стеклотекстолита и чувствительного элемента на основе кремниевой мембраны было определено значение Едmax ≈ 13000 МПа. Максимальный размер датчика 14-15 мм, минимальный 1,4-1,5 мм, что позволяет его использовать при исследовании напряжений в слоистых и блочных структурах горных массивах практически во всех используемых масштабах моделирования, при условии, что их размеры составляют не более 25-50 % от минимальных размеров отдельных блоков [6, 7].
После определения геометрических и деформационных параметров датчика была разработана окончательная конструкция миниатюрного датчика на базе кремниевого интегрального тензомодуля мембранного типа, установленного в корпусе определенной формы из стеклотекстолита с близкими к кремнию коэффициентами линейного расширения для минимизации влияния изменения температуры на его показания. На датчик были получены авторские свидетельства № 1208486 и 17778566.
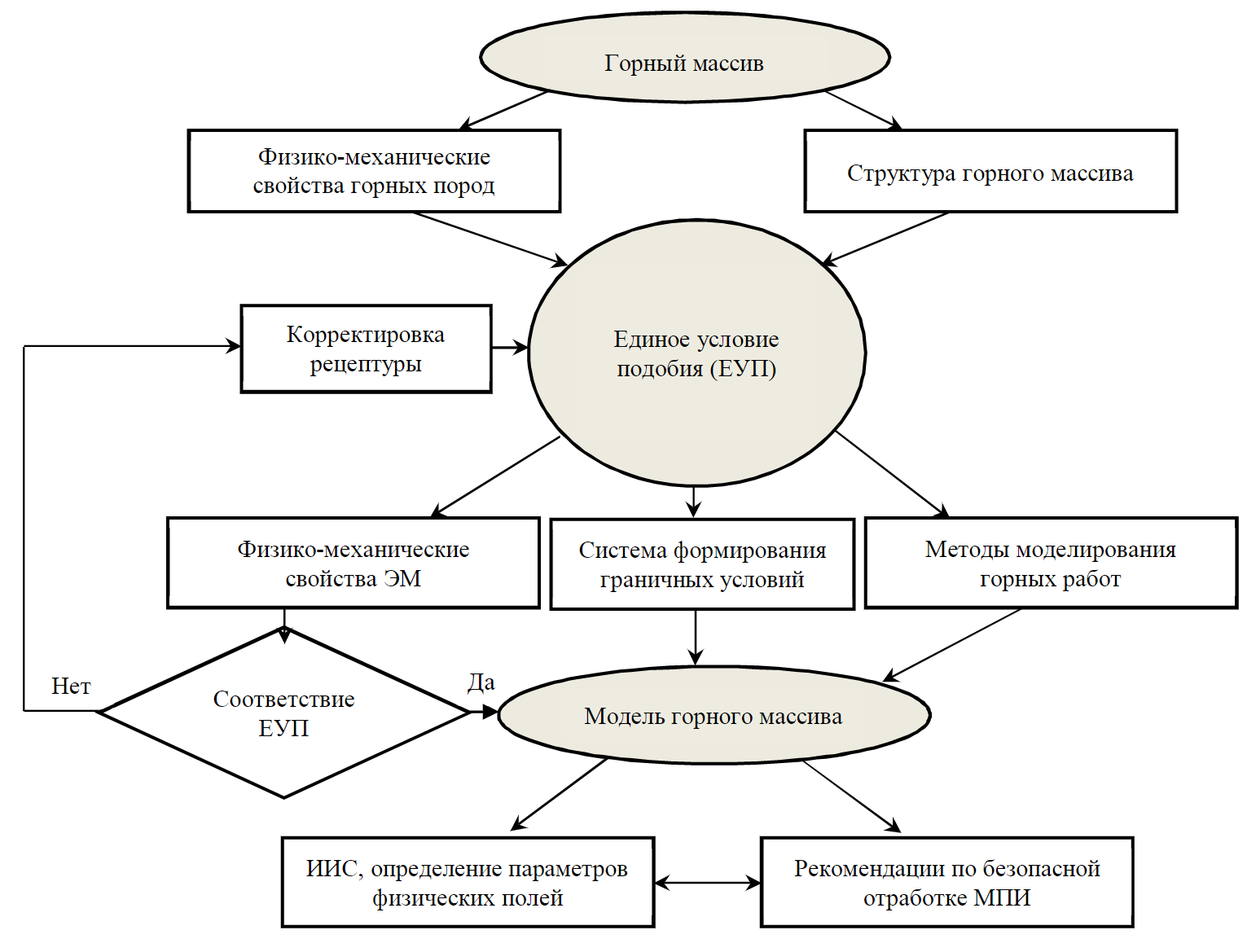
Рис.3. Принципиальная схема структуры предлагаемой методологии моделирования нелинейных геомеханических процессов на моделях из эквивалентных материалов
Проведенные экспериментальные исследования позволили определить области надежного определения напряжений при воздействии всех основных информативных и неинформативных влияющих факторов (размеры блока или толщина слоя, температура среды, контактные условия, неоднородность ЭМ, фактическое отношение модулей деформаций датчика и ЭМ, деформации пластичности и ползучести, спектры частот исследуемых напряжений).
Разработанный комплекс новых подходов к моделированию на ЭМ представляет собой совокупность теоретических и технических решений или новую методологию моделирования, схематично представленную на рис.3.
Разработанная методология была применена при изучении НДС в типовых блочных и слоистых массивах при подземной разработке полезных ископаемых (табл.1), а также при ее апробации в ходе исследования нелинейных геомеханических процессов, связанных с изменением во времени и пространстве параметров секущих трещин, отслоений, «зияющих пустот», блочных структур при разработке ряда крупных месторождений полезных ископаемых в РФ (табл.2). В табл.1, 2 приняты следующие обозначения: Kσ, Kτm – коэффициенты концентрации нормальных σ и максимальных касательных напряжений τm; ЭМ и ОЧМ – модели из эквивалентных и оптически чувствительных материалов; L или l – размеры блоков. Полученные результаты позволили получить новую информацию о глубинных процессах в горных массивах, позволяющую повысить надежность прогнозирования опасных геомеханических явлений. Более подробные данные о результатах проведенных исследований приведены в работах [7, 20, 21]. Проведена оценка достоверности (абсолютной или относительной погрешности) моделируемых или исследуемых погрешностей: размеров блока (±0,02-0,2 м) при масштабе от 1:20 до 1:200; физико-механических свойств (±5-6 %); напряжений (±6-10 %); относительных деформаций (±0,5-1 %); составляющих энергетического баланса (±12-15 %).
Таблица 1
Исследование на физических моделях закономерностей изменения НДС
|
Типовые структуры |
Методы исследований |
Исследуемые параметры |
Результаты исследований |
|
Одиночные тектонические разломы |
ЭМ, ОЧМ |
σ, τmKσ, Kτm
|
При моделировании на ОЧМ «опасного» одиночного разлома в однородном массиве с гладким плотно сжатым сместителем под углом 45° наблюдался перепад прироста τm от 20 до 60 %, при разрыве сплошности – до 80 %, в слоистом массиве при схожих диапазонах перепада τm – закономерности с резкой неоднородностью. При моделировании на ЭМ в слоистом массиве наблюдались более плавные изменения Kσ от 15 до 50 %, при моделировании приближения очистного забоя к сместителю – дополнительное увеличение максимального значения Kσ на 70 %. |
|
Пересечение двух разломов |
ЭМ |
σ, Kσ |
При моделировании последовательного прохождения очистной выработки через зону пересечения разломов под углом 45° наблюдалось значительное перераспределения напряжений относительно исходного Kσ0 (до прохождения выработки) и увеличение максимума Kσ с 5,5 до 8,0. |
|
Блочно-иерархический массив |
ЭМ |
σ |
При исследовании горного массива, представляющего иерархически соподчиненные блоки IV-VI рангов, вложенные друг в друга с соотношением размеров, равным трем, установлено, что Kσ с увеличением глубины уменьшается, но в центре блоков, с ростом средневзвешенного коэффициента трения по границам блока увеличивается, характер распределения Kσ зависит от места расположения в более крупных блоках. Под влиянием очистных горных работ происходит существенное перераспределение напряжений, отличающееся от известных закономерностей в слоистом массиве большими величинами Kσ и размерами зон влияния выработок, а также нелинейными откликами массива даже на слабые техногенные воздействия. |
|
Слоисто-блочные структуры |
ЭМ |
σ, lбл |
В слоистом горном массиве под влиянием горных работ происходят процессы, для оценки которых требуется проведение вероятностно-статистического анализа. Анализ позволил выделить детерминированные (средние) размеры блоков при вторичных осадках и их стохастические характеристики, а также сложные стохастические закономерности распределения напряжений внутри самих блоков с перепадами Kσ от 0,7 до 3,8, что стало возможным только после применения миниатюрных датчиков МДГ-3, не влияющих на развитие рассмотренных процессов. |
Таблица 2
Апробация новой методологии моделирования на ЭМ при исследовании геомеханических процессов в блочных и слоистых массивах при подземной разработке угольных и рудных месторождений
|
Месторождение |
Цель исследований |
Новые методики исследований на моделях из ЭМ |
Применяемые методы компьютерного моделирования |
Разброс результатов исследований различными методами |
Достигнутые результаты |
|
АО «Воркута-уголь» |
Установление параметров нарушения сплошности массива при отработке сближенных пластов двумя и более лавами |
Разработка новых методов моделирования очистных работ по падению и вкрест простиранию угольных пластов |
– |
– |
Установлены закономерности формирования систем секущих трещин, отслоений, зияющих пустот в двух взаимно перпендикулярных сечениях слоистого горного массива при отработке сближенных пластов двумя и более лавами с учетом развития процессов во времени после завершения очистных работ в лавах. |
|
ОАО «СУЭК-Кузбасс» |
Комплексная оцен-ка изменения параметров физических полей при динамических обрушениях кровли |
Применение комплекса новых датчиков, ИИС и оптических регистрирующих устройств, практический метод оценки составляющих энергетического баланса |
– |
– |
Доказана возможность локации очагов разрушения элементов модели, установлен факт существенного изменения частот колебания элементов массива и их ускорений при обрушении основной кровли, установлен колебательный характер изменения напряжений в зонах опорного давления, характеризуемый динамическим изменением максимума напряжений и его перемещением относительно поверхности обнажения, определены параметры отдельных составляющих энергетического баланса. |
|
ПАО «Уралкалий» |
Оценка опасности нарушения сплошности водозащитной толщи и определение параметров нарушенности на потенциально опасных участках |
Воспроизведение соотношений Rсж/Rр в широких пределах, решение обратной геомеханической задачи исследования процессов сдвижений при наличии надежных исходных данных только о ФМС горных пород и параметров мульды сдвижений дневной поверхности |
– |
– |
В условиях сложности или невозможности получения надежных исходных данных о характере деформирования и разрушения элементов систем разработки продуктивных пластов при оценке опасности прорыва в рудник вод или соляных растворов [5] разработана общая методика решения обратных задач методами моделирования на ЭМ при наличии натурных данных о развитии мульды сдвижений во времени путем воспроизведения на моделях процессов сдвижений от горизонтов продуктивных пластов до дневной поверхности для выявления возможности образования сплошных водопроводящих каналов и механизма их формирования. |
|
Яковлевское месторождение КМА |
Прогноз сохранности предохранительного целика с учетом отработки заходками с увеличенными параметрами |
Решение геомеханической задачи на двух разномасштабных моделях для учета влияния изменения технологии отработки продуктивных пластов на процессы сдвижений, а также обратной геомеханической задачи на основе данных о мульдах сдвижений на горизонте продуктивных пластов и дневной поверхности |
Программный комплекс RS2 Rocscience |
10-15 % |
Разработана методика физического моделирования, позволяющая исследовать процессы сдвижений и оценивать параметры наклонов и кривизны мульды на различных горизонтах – от защитного целика (рудной потолочины) до земной поверхности с учетом изменения технологии разработки рудного месторождения. Установлено, что экстремальные значения кривизны потолочины и верхней границы защитного целика не превышают критических значений, при которых возможно образование водопроводящих трещин. |
|
Коробковское месторождение железистыхкварцитов |
Обоснование порядка разработки месторождения |
Моделирование ФМС горного массива с учетом коэффициента структурного ослабления при различном порядке отработки горизонтов и определение параметров НДС и процессов сдвижений |
Simulia Abaqus3DEC |
10-20 % |
Установлен рекомендуемый порядок отработки месторождения, при котором вертикальные осадки дневной поверхности не превышают допустимых пределов. |
|
Рудник «Известняки» Норильского промрайона |
Разработки рекомендаций по выбору параметров конструктивных элементов системы разработки и способов поддержания кровли |
Моделирование НДС в элементах системы разработки при варьировании ее параметров |
Программный комплекс «Press3D Ural» |
5-15 % |
Методы и средства физического моделирования на эквивалентных материалах позволили воспроизвести камерно-столбовую систему разработки при ведении очистных работ с формированием вентиляционных окон для проветривания выработок за счет общешахтной депрессии, оценить неоднородность нагружений целиков, определить коэффициент запаса устойчивости |
Заключение
- Изложены научно обоснованные принципы обеспечения подобия при воспроизведении и исследовании на моделях из эквивалентных материалов динамических геомеханических процессов при подземной разработке твердых полезных ископаемых в блочных и слоистых массивах на основе универсального единого условия подобия напряжений, деформаций и основных составляющих энергетического баланса.
- Разработаны новые типы ЭМ, удовлетворяющие комплексному критерию подобия и позволяющие моделировать различные структуры блочных и слоистых массивов.
- Доказано, что использование разработанной системы автоматизированного управления обеспечивает воспроизведение изменения различных видов напряженно-деформированного состояния на границе исследуемой области массива, обусловленных природными или техногенными факторами, в широком диапазоне функциональных параметров – режимах заданных нагрузок, деформаций или смешанных режимах.
- Разработаны научные основы определения как квазистатических, так и динамических напряжений на основе созданных средств измерений в отдельных разномасштабных структурированных областях массива, при подвижках в блочно-иерархических массивах, а также при эволюции структурных параметров массивов под влиянием горных работ.
- Установлены закономерности развития динамических процессов деформирования, разрушения и перемещения отдельных структурированных элементов массива в широком диапазоне скоростей и ускорений под влиянием сил гравитации и накопленной в них упругой энергии, что позволяет учитывать динамические параметры физических и геофизических полей при оценке возможных опасных последствий динамических явлений.
- Установлены детерминированные (средние) размеры блоков при вторичных осадках и их стохастические характеристики, а также сложные стохастические закономерности распределения напряжений внутри самих блоков с перепадами коэффициентов концентраций напряжений в них от 0,7 до 3,8.
- Установлено, что величина нормальных напряжений в центре иерархически соподчиненные блоков IV, V и VI ранга, вложенных друг в друга с соотношением размеров, равным трем, уменьшается при увеличении глубины залегания и увеличивается при увеличении средневзвешенного трения по границам.
- Доказана эффективность применения разработанной методики решения на моделях из эквивалентных материалов обратных геомеханических задач с целью воспроизведения известной динамики изменения дневной мульды сдвижений для получения данных о параметрах сдвижений и нарушений сплошности в массиве на различных горизонтах.
- Установлены закономерности формирования системы водопроводящих трещин и отслоений в массиве горных пород при отработке продуктивных пластов калийных месторождений, дана оценка условий образования сквозных водопроводящих каналов.
- Дана оценка достоверности применения метода моделирования на эквивалентных материалах при моделировании динамических геомеханических процессов в зависимости от точности воспроизведения геометрических параметров структур массива, физико-механических характеристик горных пород, начальных и граничных условий, а также точности определения параметров физических полей в самой модели.
Литература
- Бадтиев Б.П. Исследования на моделях из эквивалентных материалов эффективности способов борьбы с пучением путем изменения формы поперечного сечения выработок / Б.П.Бадтиев, И.А.Сальвассер, С.В.Кузьмин // Маркшейдерский вестник. 2015. № 4 (107). С. 51-55.
- Басов В.В. Исследование характера деформирования эквивалентного материала для тестирования численной модели прогноза устойчивости сопряжений горных выработок / В.В.Басов, С.В.Риб, В.Н.Фрянов // Известия Тульского государственного университета. Науки о Земле. 2017. Вып. 2. С. 134-145.
- Басов В.В. Подбор эквивалентного материала для физического моделирования геомеханических процессов в окрестности подготовительных выработок угольных шахт / В.В.Басов, С.В.Риб // Вестник Сибирского государственного индустриального университета. 2016. № 4 (18). С. 32-35.
- Басов В.В. Характер распределения деформаций при физическом моделировании углепородного массива в окрестности сопряжений горных выработок // Вестник Забайкальского государственного университета. 2017. Т. 23. № 8. С. 25-32. DOI: 10.21209/2227-9245-2017-23-8-25-32
- Гусев В.Н. Определение параметров зоны водопроводящих трещин через горизонтальные деформации подрабатываемой толщи / В.Н.Гусев, Д.А.Илюхин, А.Г.Алексенко // Записки Горного института. 2013. Т. 204. С. 69-73.
- Зуев Б.Ю. Определение статических и динамических напряжений в физических моделях слоистых и блочных породных массивов / Б.Ю.Зуев, В.П.Зубов, А.Д.Смычник // Горный журнал. 2019. № 7. С. 61-66. DOI: 10.17580/gzh.2019.07.02
- Зуев Б.Ю. Разработка методов и технических средств определения статических и динамических напряжений в физических моделях слоистых и блочно-иерархических горных массивах // Горный информационно-аналитический бюллетень. 2014. № 4. С. 351-355.
- Зуев Б.Ю. Физическое моделирование геомеханических процессов в блочно-иерархических массивах на основе единого комплексного условия подобия // Горный информационно-аналитический бюллетень. 2014. № 4. C. 356-360.
- Зубов В.П. Применяемые технологии и актуальные проблемы ресурсосбережения при подземной разработке пластовых месторождений полезных ископаемых // Горный журнал. 2018. № 6. С. 77-83. DOI: 10.17580/gzh.2018.06.16
- Зубов В.П. Снижение рисков затопления калийных рудников при прорывах в горные выработки подземных вод / В.П.Зубов, А.Д.Смычник // Записки Горного института. 2015. Т. 215. С. 29-37.
- Кузьмин С.В. Разработка способа охраны подготовительных выработок с помощью компенсационных полостей при отработке мощных пологих угольных пластов: Автореф. дис. … канд. техн. наук. СПб: Санкт-Петербургский горный университет, 2017. 19 с.
- Манько А.В. О создании модели расчета трещиноватых скальных массивов при тектонических нагрузках методом эквивалентных материалов / А.В.Манько, С.В.Влад // Инженерный вестник Дона. 2015. № 2-2 (36). C. 87.
- Неверов А.А. Сравнительный анализ численного и физического моделирования напряженно-деформированного состояния массива горных пород / А.А.Неверов, С.А.Неверов, С.Ю.Васичев // Вестник Кузбасского государственного технического университета. 2013. № 4 (98). С. 14-22.
- Повышение безопасности рудников при отработке Верхнекамского месторождения калийно-магниевых солей / В.П.Зубов, Е.Р.Ковальский, С.В.Антонов, В.В.Пачгин // Горный информационно-аналитический бюллетень. 2019. № 5. C. 22-33. DOI: 1025018/0236-1493-2019-05-0-22-33
- Развитие систем моделирования и проектирования горных машин в КузГТУ и КарГТУ Российской Федерации и Казахстана / Г.Д.Буялич, Г.С.Жетесова, К.М.Бейсембаев, Н.С.Малыбаев // Международный журнал прикладных и фундаментальных исследований. 2016. № 5. Ч. 1. С. 8-13.
- Риб С.В. Лабораторный стенд для определения деформаций горных пород в окрестности выработки на пластах сложного строения // Наукоемкие технологии разработки и использования минеральных ресурсов. Вып. 3. Новокузнецк: Сибирский государственный индустриальный университет, 2017. С. 155-157.
- Риб С.В. Разработка комплексного метода исследования геомеханических процессов при интеграции численного и физического моделирования / С.В.Риб, Ю.М.Говорухин // Известия Тульского государственного университета. Науки о Земле. 2018. Вып. 2. С. 363-378.
- Риб С.В. Физическое моделирование геомеханических процессов в окрестности горной выработки / С.В.Риб, В.В.Басов // Вестник Сибирского государственного университета. 2017. № 4 (22). С. 45-50.
- Сергиенко А.И. Исследование поведения породного массива на моделях из эквивалентных материалов / А.И.Сергиенко, Ю.С.Мостыка // Геотехнології і охорона праці у гірничій промисловості збірник матеріалів: VII регіональної науково-практичної конференції. Красноармейск: KIIДонНТУ, 2015. C. 76-82.
- Физическое моделирование динамических явлений при подземной разработке полезных ископаемых / Б.Ю.Зуев, С.В.Цирель, Р.С.Истомин, М.Е.Мельницкая // Горный информационно-аналитический бюллетень. 2015. S60-2. С. 117-127.
- Физическое моделирование формирования зон разрушения в области влияния очистных горных работ // Инновационные направления в проектировании горнодобывающих предприятий: геологическое обеспечение проектирования и сопровождения горных работ: Сборник научных трудов / Б.Ю.Зуев, Н.В.Кротов, Р.С.Истомин, М.Е.Мельницкая, А.А.Вьюников. СПб: Санкт-Петербургский горный университет, 2017. С. 412-417.
- Хоменко О.Е. Лабораторные исследования зонального структурирования массива вокруг горных выработок / О.Е.Хоменко, М.Н.Кононенко, А.П.Дронов // Физико-технические проблемы горного производства. 2016. Вып.18. С. 103-110.
- Хозяйкина Н.В. Обрушение пород кровли в лавах пологопадающих угольных пластов. Днепропетровск: Нацiональний гiрничий университет, 2012. 126 с.
- A Novel Longwall Mining Layout Approach for Extraction of Deep Coal Deposits / Pengfei Wang, Jingli Zhao, Yoginder P. Chugh, Zhiqiang Wang // Minerals. 2017. Vol. 7. Iss. 4. № 60. DOI: 10.3390/min7040060
- Comprehensive Study of Strata Movement Behavior in Mining a Longwall Top Coal Caving Panel of a Composite Coal Seam with Partings / Hongtao Liu, Linfeng Guo, Guangming Cao, Xidong Zhao et al. // Applied sciences. 2020. Vol. 10. Iss. 10. № 5311. DOI:10.3390/app10155311
- Effect of Sand Particle Size on Microstructure and Mechanical Properties of Gypsum-Cemented Similar Materials / Weiming Guan, Qi Qi, Zhiyi Zhang, Senlin Nan // Materials. 2020. Vol. 13. Iss. 3. № 765. DOI: 10.3390/ma13030765
- Experimental Investigation of the Progressive Failure of Multiple Pillar-Roof System / Zilong Zhou, Lu Chen, Xin Cai et al. // Rock Mechanics and Rock Engineering. 2018. Vol. 51. P. 1629-1636. DOI: 10.1007/s00603-018-1441-1
- Gaofeng Song. Evaluation of the face advance rate on ground control in the open face area associated with mining operations in Western China / Gaofeng Song, Zhenwei Wang, Kuo Ding // Journal of Geophysics and Engineering. 2020. Vol. 17. Iss. 2. P. 390-398. DOI: 10.1093/jge/gxz124
- Ground cracks development and characteristics of strata movement under fast excavation: a case study at Bulianta coal mine, China / Yuankun Xu, Kan Wu, Liang Li et al. // Bulletin of Engineering Geology and the Environment. 2017. Vol. 78. P. 325-340. DOI: 10.1007/s10064-017-1047-y
- Kan Wu. Experimental research on dynamic movement in strata overlying coal mines using similar material modeling / Kan Wu, Gong-Lin Cheng, Da Wei Zhou // Arabian Journal of Geosciences. 2015. Vol. 8. P. 6521-6534. DOI: 10.1007/s12517-014-1685-3
- Physical and numerical investigation of bedding adhesion strength on stratified rock roof fracture with longwall coal mining / Mighe Ju, Dapeng Wang, Jingcheng Shi et al. // Geomechanics and Geophysics for Geo-Energy and Geo-Resources. 2021. Vol. 7. № 24. DOI: 10.1007/s40948-020-00209-2
- Three-Dimensional Physical and Numerical Modelling of Fracturing and Deformation Behaviour of Mining-Induced Rock Slopes / Guoxiang Yang, Anthony K. Leung, Nengxiong Xu et al. // Applied sciences. 2019. Vol. 9. Iss. 7. № 1360. DOI: 10.3390/app9071360
- Wan-rong Liu. Experimental and Numerical Study of Rock Stratum Movement Characteristics in Longwall Mining // Hindawi, Shock and Vibration. 2019. Vol. 2019. № 5041536. DOI: 10.1155/2019/5041536
- Zuev B.Yu. Application prospects for models of equivalent materials in studies of geomechanical processes in underground mining of solid minerals / B.Yu.Zuev, V.P.Zubov, A.S.Fedorov // Eurasian mining. 2019. №1. P. 8-12.
