Физико-математическая модель разрушения горных пород  зубом фрезерной установки

С. А. Шемякин; Е. А. Шишкин

doi:10.31897/PMI.2021.5.3

Том 251

Страницы:

639-647

Скачать том:

RUS ENG

Научная статья

Геотехнология и инженерная геология

Физико-математическая модель разрушения горных пород зубом фрезерной установки

Авторы:

С. А. Шемякин¹

Е. А. Шишкин²

Об авторах

1 — д-р техн. наук профессор Тихоокеанский государственный университет ▪ Orcid ▪ Elibrary ▪ Scopus
2 — канд. техн. наук доцент Тихоокеанский государственный университет ▪ Orcid ▪ Elibrary ▪ Scopus

Дата отправки:

2021-03-05

Дата принятия:

2021-10-18

Дата публикации:

2021-10-29

Аннотация

В результате анализа работ по разрушению пород резцами фрезерных установок установлено, что существующие разработки не дают возможности перейти к выводу расчетных зависимостей для определения сопротивлений разрушению, либо могут быть использованы только в предварительных расчетах параметров известных по конструкции фрезерных установок. Для устранения указанных недостатков была разработана комбинированная физико-математическая модель процесса взаимодействия одиночного резца со сферическим наконечником с породой. Рассмотрение физической картины действия сил и напряжений со стороны резца со сферическими наконечниками на отделяющийся элемент породы в предельном состоянии позволило аналитически описать составляющие полного сопротивления, являющиеся математической частью физико-математической модели разрушения пород резцами. Получены аналитические зависимости для определения касательной и нормальной составляющих сопротивления разрушению пород средней крепости. Проведена проверка адекватности физико-математической модели физическому процессу разрушения пород различной крепости резцом на универсальном стенде как в полевых, так и в лабораторных условиях. Техническая оценка результатов экспериментальных исследований подтверждает достоверность разработанной физико-математической модели.

Ключевые слова:

горные породы фрезерные установки процесс разрушения резцы сопротивление разрушению физико-математическая модель стенд

10.31897/PMI.2021.5.3

Введение

Большим достижением в развитии безвзрывных технологий открытых и подземных горных ра-бот является создание фрезерных установок и комбайнов, способных разрабатывать достаточно крепкие породы с прочностью на сжатие 50-80 МПа и более [11, 13]. В случае разработки поро-ды с коэффициентом крепости по шкале М.М.Протодьяконова до ƒ = 2, фрезы оснащают клиновидными зубьями (рис.1, а), поскольку при большей крепости их режущие кромки обламываются и инструмент начинает работать неэффективно [9]. При разрушении породы с коэффициентом крепости больше ƒ = 2, резцы (рис. 1, б) со сферическим наконечником [8, 10]. В настоящее время производители фрезерных установок и комбайнов оснащают рабочие органы машин резцами данного типа [23]. Это обусловлено рядом преимуществ сферических резцов в сравнении с клиновидными, среди которых повышенная глубина резания, симметричный износ, высокая надежность [24, 27, 41].

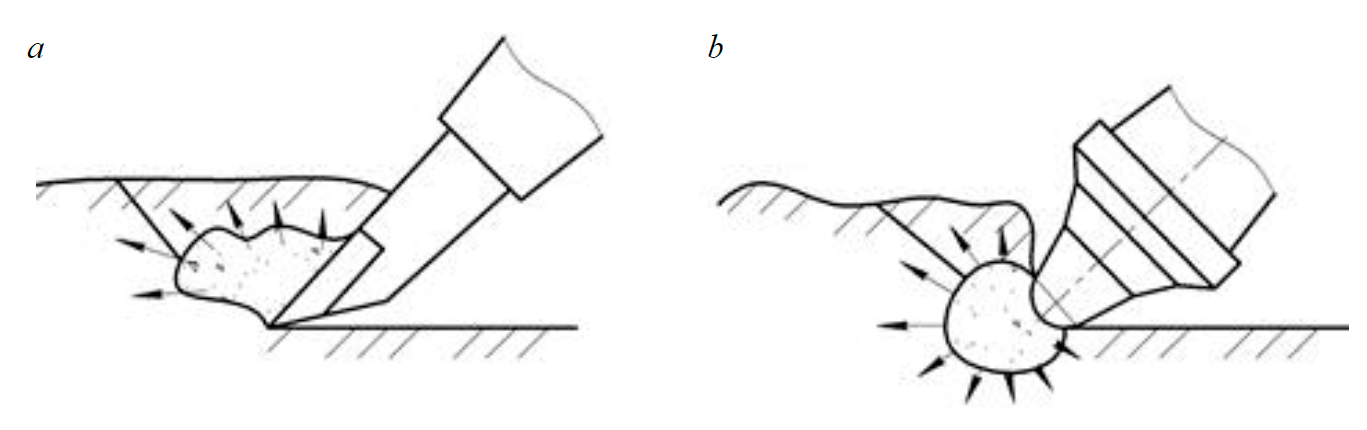
Рис.1. Схема взаимодействия клиновидного резца с породой (а) и сферическим наконечником с крепкой породой (б)

Процессу разрушения клиновидным зубом мерзлых и талых мелкозернистых пород, в том числе с крупнообломочными включениями, посвящено большое число научных работ [2-4]. Существуют физико-математические модели [16, 19, 40] и надежные по точности расчетные зависимости для определения сопротивления разрушению [17, 18, 39].

Процесс взаимодействия резца со сферическим наконечником с породой сложен и мало изучен. Существуют научные разработки по моделированию процесса разрушения пород рез-цами со сферическим наконечником на основе методов конечных элементов [14, 22, 28, 30], дискретных элементов [34, 35, 37], конечных разностей [36]. Эти разработки позволяют пред-ставить распространение напряжений внутри породы от давления резца, однако не дают воз-можности перейти к выводу расчетных зависимостей для определения сопротивлений разруше-нию и к расчету необходимого крутящего момента на фрезерном рабочем органе и потребной мощности на приводе фрезы, а также всей машины в целом.

Определенный интерес представляет концепция определения параметров фрезерной уста-новки на основе корреляционных связей между прочностью породы на одноосевое сжатие и со-противление разрушению [33, 38], а также потребной мощностью и расходом топлива [14, 26]. Такой метод может быть использован в предварительных расчетах параметров известных по конструкции фрезерных установок, но при создании новых типов машин требуются уточненные зависимости для определения сопротивлений разрушению отдельным резцом, а, следовательно, и потребного момента на фрезе, потребной мощности и т.д.

Есть попытки моделирования процесса работы фрезерных рабочих органов с математиче-ской точки зрения [12, 32] без рассмотрения физической сущности разрушения породы резцом со сферическим наконечником. Однако, полученные уравнения для определения крутящих мо-ментов на фрезе [6, 7] без указания прочностных характеристик разрабатываемой резцами по-роды практического применения не имеют.

Определенное практическое значение имеют экспериментальные исследования процесса разрушения резцами со сферическим наконечником, проведенные в Австралии [29, 31], а также в институте угля СО РАН и Кузбасском государственном техническом университете [1].

Полученные в результате экспериментов регрессионные уравнения дают возможность определять сопротивление разрушению для ограниченного числа пород, на которых проводи-лись опыты.ми со сферическим наконечником, проведенные в Австралии [29, 31], а также в институте угля СО РАН и Кузбасском государственном техническом университете [1].

Следует отметить математическую модель разрушения горной породы, имеющую модифи-цированный вариант, учитывающий износ резца [21]. Модель позволяет определять значение усилия резания на радиальном резце при разрушении различных типов горных пород. Удовле-творительная сходимость результатов экспериментальных исследований с результатами теоре-тического моделирования позволяют сделать вывод об адекватности модели. Однако предлага-емая модель имеет ряд допущений: горная масса считается однородной изотропной средой, не учитывается взаимное влияние соседних резцов на процесс разрушения горной массы (т.е. шаг резания).

Известна модель взаимодействия резца, оснащенного сферическим наконечником, с поро-дой, позволяющая определять значение максимального сопротивления породы разрушению [20]. Несмотря на удовлетворительную сходимость результатов моделирования [25], в предла-гаемой модели не учитывается трение, неизбежно возникающее между резцом и породой. Кро-ме этого, при разработке модели принято упрощение о равномерности распределения давления по площадке контакта режущего инструмента и породы, что не позволяет учесть упругую со-ставляющую процесса разрушения.

Значительный вклад в исследование процесса разрушения горной породы внесли В.В.Нескромных и К.Н.Борисов [5], которые разработали схему разрушения-скалывания поро-ды резцом бурового долота, а также выявили роль ядра смятия на касательную составляющую сопротивления разрушению и предложили упрощенную зависимость для ее определения через напряжения скола. При всей важности выполненной работы следует отметить, что в механике деформируемого твердого тела не употребляют понятия напряжения скола. Известны напряже-ния сжатия, растяжения, сдвига и смятия. Как и чем определять напряжения скола на практике – неизвестно. Кроме того, эти исследователи не учитывают сопротивления, связанные с продви-жением ядра смятия в массиве породы, а также трение по площадке затупления [5]. В полной мере применить схему (физико-математическую модель) разрушения-скалывания к резцам со сферическим наконечником затруднительно, поскольку по конструктивным признакам эти рез-цы существенно отличаются друг от друга.

Анализ научных источников свидетельствует об актуальности разработки комбинирован-ной физико-математической модели процесса взаимодействия с породой одиночного резца со сферическим наконечником.

Методология

Наблюдения во время многочисленных и длительных экспериментальных исследований в Тихоокеанском государственном университете процесса разрушения мерзлых мелкозернистых, сланцевых пород, а также бетона резцами с наконечниками клиновидной и сферической формы показывают, что дно прорези, оставляемой резцом, имеет всегда гладкую поверхность, а отделяемые куски (элементы) породы – неровную (рваную). Неровность поверх-ности отделяемых элементов породы свидетельствует о том, что в конечном итоге отделение идет за счет напряжений разрыва. Перед резцом в нижней части прорези формируется ядро смятия, ко-торое оказывает давление на вышележащий слой породы и вызывает отделение элементов по-роды тогда, когда наступает предельное состояние. В предельном состоянии давление со сто-роны ядра смятия на вышележащий слой породы равно сопротивлению отделения верхнего слоя. На рис.2 изображена схема предельного состояния взаимодействия с породой резца со сферическим наконечником в момент отделения верхнего слоя. Это изображение и есть физиче-ская модель процесса разрушения породы.

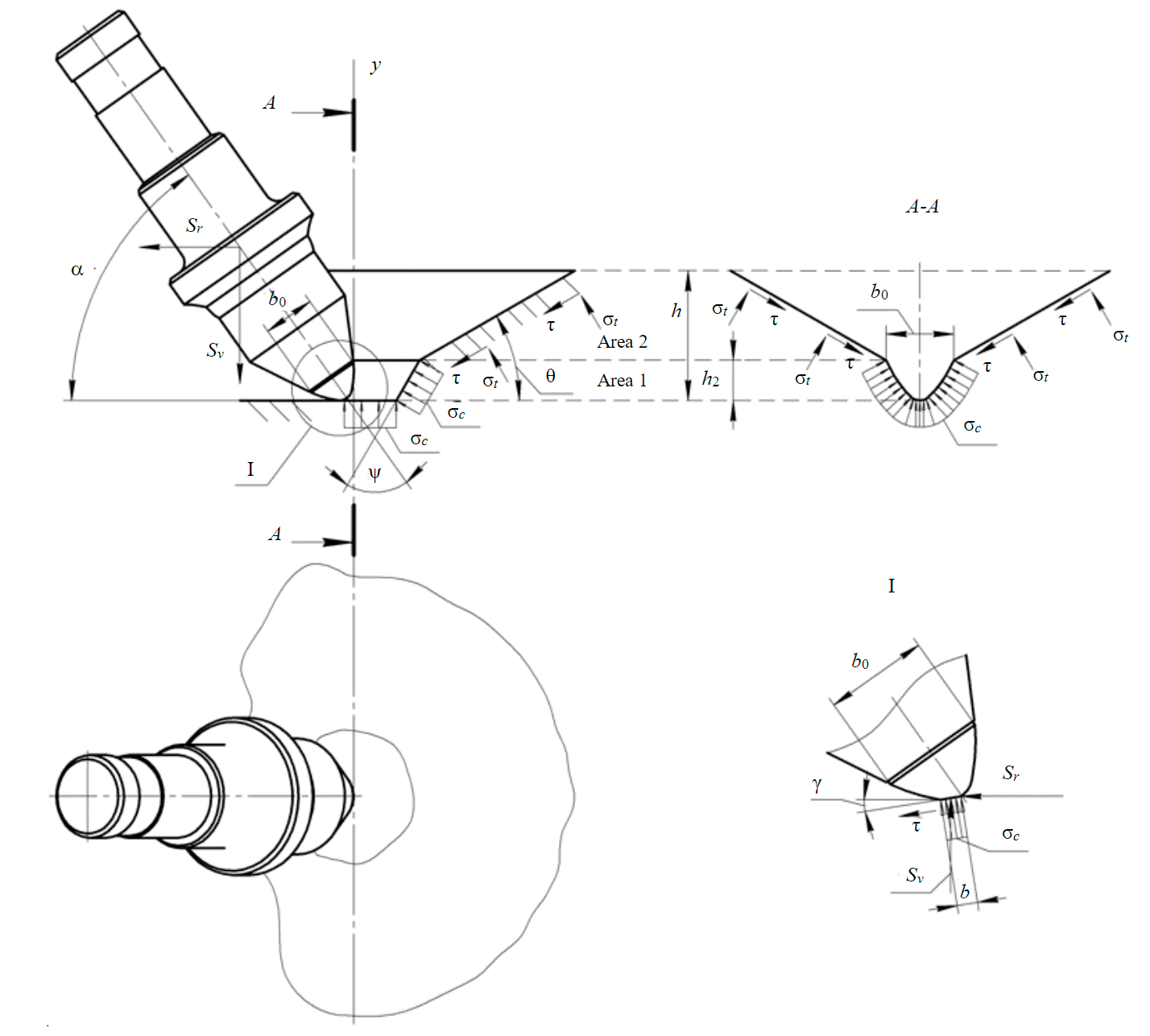
Рис.2. Физическая картина действия сил и напряжений со стороны резца на отделяющийся элемент породы в предельном состоянии

Целесообразно эту схему разбить на две области. Первая область – это поверхность, огра-ниченная ядром смятия. Высота этой области h₂, ширина ограничена боковыми поверхностями сферического наконечника, а внизу основанием ядра смятия. Первая область изображена на рис.3, а, вторая – область отделения – на рис.3, б.

Рассмотрение приведенной на рис.3 физической модели процесса разрушения позволяет приступить к аналитическому определению составляющих полного сопротивления, а именно к математической части общей комбинированной модели.

Горизонтальная составляющая сопротивления разрушению есть сумма горизонтальных со-ставляющих в первой и второй области прорези:

S_{h} = S_{h 1} + S_{h 2} . (1)

Нормальная составляющая представляет собой

S_{υ} = S_{υ 1} + S_{υ 2} . (2)

В свою очередь,

S_{h 1} = S_{x 1} + T_{1} + S_{h}^{m}, (3)

где S_x1 горизонтальная составляющая давления на лобовую поверхность ядра уплотнения.

Если выделить на лобовой поверхности ядра уплотнения полукруглую полосу шириной dt, то действующая перпендикулярно к элементарной площадке dF₁ сила будет равна

d S = σ_{c} d F_{1} = σ_{c} d t r d ρ . (4)

Horizontal projection

d S_{x 1} = σ_{c} d t r d ρ c o s α_{2} . (5)

Полное давление на лобовую поверхность ядра уплотнения

S_{x 1} = σ_{c} l 2 \int_{0}^{π / 2} c o s ρ d ρ \int_{r 1}^{r 2} r d r c o s α_{2}; (6)

учитывая, что h₂/l = cosaα₂, l = h₂/cosα₂, после интегрирования

S_{x 1} = σ_{c} h_{2} (r_{2} - r_{1}) . (7)

Сила трения ядра уплотнения по нижней грани

T_{1} = σ_{c} \frac{π r_{1}^{2}}{2} f, (8)

где ƒ – коэффициент трения породы о породу; r₁ – радиус ядра уплотнения по нижней его грани.

Касательная составляющая силы трения резца на площадке затупления (рис.3, а)

S_{r}^{m} = \frac{σ_{c} π b^{2} s i n (γ+μ)}{4 c o s μ}, (9)

где μ угол трения породы о сталь; b – диаметр площадки затупления.

Нормальная составляющая в области 2

S_{υ 1} = S_{y 1} + S_{t} + S_{b}^{m}, (10)

где S_y₁ – сила давления сминающих напряжений на лобовую грань ядра уплотнения; S_t – сила давления сминающих напряжений на торцевую грань ядра уплотнения; $S_{b}^{m}$ ; – нормальная составляющая силы трения о площадку износа;

S_{y 1} = S_{x 1} tg α_{2} = σ_{c} h_{2} (r_{2} - r_{1}) tg α_{2}; (11)

S_{t} = σ_{c} F = σ_{c} \frac{π r_{1}^{2}}{2}, (12)

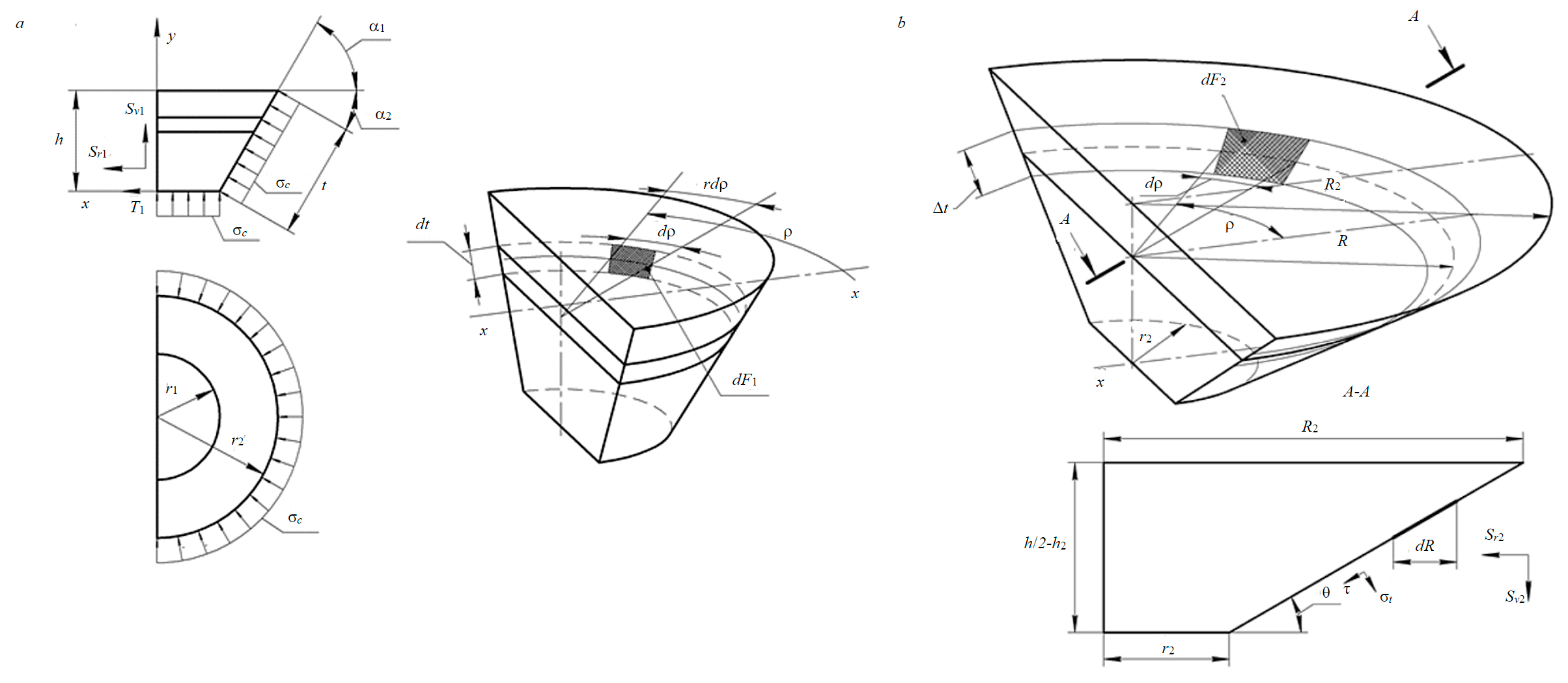
Рис.3. Схемы действия сил и напряжений в предельном состоянии на отделяемый элемент породы: а – область ядра смятия; б – область отрыва

$F = π r_{1} / 2$ ; – площадь торцевой грани ядра уплотнения;

S_{b}^{m} = \frac{σ_{c} π b^{2} cos (δ_{1} + μ)}{4 cos μ} . (13)

Касательная составляющая сопротивления разрушению в области 2 (см. рис.2) может быть определена путем интегрирования нормальных σ и касательных τ напряжений. Область породы 2 представляет собой половину усеченного конуса. Высота усеченного конуса равна h – h₂, а угол наклона поверхности отделения θ (рис.3, б). Если выделить на поверхности отделения радиусом R полосу шириной dl, а на полосе обозначить бесконечно малую полосу dF = dldrR, то усилия на эту элементарную площадку будут равны: в горизонтальном направлении

d S_{r 2} = - σ_{t} R \frac{d R}{c o s θ} d ρ s i n θ c o s ρ + τ R \frac{d R}{c o s θ} d ρ c o s θ c o s ρ, (14)

в вертикальном направлении

d S_{b 2} = - σ_{t} R \frac{d R}{c o s θ} d ρ c o s θ c o s ρ - τ R \frac{d R}{c o s θ} d ρ s i n θ s i n ρ . (15)

После интегрирования уравнений (14) и (15) по dr и dR получим

S_{r 2} = (\frac{τ cosθ - σ_{t} sinθ}{cosθ}) \int_{0}^{π / 2} \int_{r_{2}}^{R_{2}} cosρ R d ρ d R = ({τ-σ}_{t} tgθ) {2 sinρ|}_{0}^{π / 2} {\frac{R^{2}}{2}|}_{r_{2}}^{R_{2}}; (16)

S_{b 2} = - (τtgθ + σ_{t}) {\cdot 2 sinρ|}_{0}^{π / 2} {\frac{R^{2}}{2}|}_{r_{2}}^{R_{2}} . (17)

Если принять допущение, что r₂ = b₀/2, где b₀ – диаметр резца в месте установки твердосплавного наконечника, то

R_{2} = \frac{b_{0}}{2} + \frac{h - h_{2}}{tgθ} . (18)

После подстановки в (16) и (17) пределов интегрирования получим

S_{r 2} = ({τ-σ}_{t} tgθ) [\frac{h - h_{2}}{{tg}^{2} θ} (b_{0} tgθ + h - h_{2})]; (19)

S_{b 2} = - (τtgθ + σ_{t}) [\frac{h - h_{2}}{{tg}^{2} θ} (b_{0} tgθ + h - h_{2})] . (20)

Путем сложения составляющих сопротивлений в областях 1 и 2, а также сопротивлений, связанных с затуплением, определяются расчетные зависимости полного сопротивления разру-шению породы резцом со сферическим наконечником. Таким образом

S_{r} = σ_{c} [h_{2} (r_{2} - r_{1}) + \frac{π r_{1}^{2}}{2} f + \frac{π b^{2} sin (γ+μ)}{4 cosμ}] - (τ - σ_{t} tgθ) [\frac{h - h_{2}}{{tg}^{2} θ} (b_{0} tgθ + h - h_{2})]; (21)

S_{b} = σ_{c} [h_{2} (r_{2} - r_{1}) t g α_{2} + \frac{π r_{1}^{2}}{2} + \frac{{πb}^{2} cos (δ_{1} +μ)}{4cosμ}] - (τ tgθ + σ_{t}) [\frac{h - h_{2}}{{tg}^{2} θ} (b_{0} tgθ + h - h_{2})] . (22)

Рис.4. Стенд для разрушения пород 1 – насосная станция; 2 – гидрораспределитель; 3 – тяговый гидроцилиндр; 4 – направляющие балки; 5 – опорные стойки; 6 – тензометрическая тележка; 7 – резец; 8 – блок породы; 9 – блок тензометрической аппаратуры

С целью проверки функциональных зависимостей (21), (22), составляющих основу разработанной физико-математической модели, на сходимость с экспериментальными значениями были проведены опыты по разрушению резцами фрезерного комбайна Wirtgen 2600SM некоторых пород и материалов – мерзлый песок, относящийся по шкале М. М.Протодьяконова к VI категории с коэффициентом крепости 2; сланец средней крепости V категории с коэффициентом крепости 4; бетон с прочностью на сжатие 60 МПа и плотностью 2320 кг/м³. Разрушение проводилось на универсальном стенде (рис.4) как в полевых, так и в лабораторных условиях. Опыты по разрушению сланцевых пород осуществлялись непосредственно в карьере, при этом стенд агрегатировался с трактором.

При испытании пород на срез со сжатием и растяжение косвенным методом диаметрально-го сжатия использовались образцы высотой 100 мм и диаметром 71,4 мм. Напряжения смятия определялось путем вдавливания в породу стального пуансона с помощью универсальной ис-пытательной машины УММ-50 (ГОСТ 7855-61).

Стенд для разрушения пород работает следующим образом. По направляющим в балках 4 перемещается тензометрическая тележка 6, несущая рабочий орган 7. Разрушение породы 8 происходит послойно. Толщина стружки изменяют при помощи винтового устройства. Кон-струкцией стенда предусмотрена постановка его на лыжи и сцепка с тяговой машиной. Это дает возможность проводить эксперименты в полевых условиях.

В ходе экспериментальных исследований определялись параметры оставляемой резцом прорези: угол развала θ [15], углы α₁, α₂, высота h₂, а также размеры r₁ и r₂, определяющие форму ядра уплотнения. Выполнить такие замеры на крепких породах достаточно просто, поскольку ядра уплотнения часто отделяются вместе с областью отрыва, а вид и цвет ядер уплотнения значительно отличаются от породы в области отрыва.

Обработка зафиксированных максимальных значений составляющих сопротивлений разрушению по осциллограммам S_r и S_b вполне согласуется с результатами расчета по зависимостям (21), (22) разработанной математической модели процесса разрушения пород резцами фрезерных комбайнов. Результаты расчета, полученные по зависимостям (21), (22), отличаются от экспериментальных не более, чем на 12-13 %, что свидетельствует о правильности принятых исходных положений при разработке физико-математической модели.

Заключение

Разработанная физико-математическая модель процесса разрушения горных пород одиночным резцом со сферическим наконечником и полученные аналитические зависимости для определения касательной и нормальной составляющих сопротивления разрушению дают обоснованную возможность при известной крепости породы, количестве резцов и их траектории движения по забою вычислять крутящие моменты на рабочих органах фрезерных установок, потребную мощность на их привод и, следовательно, фактическую производительность.

Литература

Герике П.Б. Поиск инструмента для механического разрушения прочных породных массивов / П.Б.Герике, Б.Л.Герике // Горный информационно-аналитический бюллетень. 2012. № S2. С. 241-265. URL: https://elibrary.ru/item.asp?id=21571762
Зайцев В.И. Эффективность использования долот PDС / В.И.Зайцев, А.В.Карпиков, В.В.Че // Науки о Земле и недропользование. 2014. № 5 (48). С. 58-66. URL: http://journals.istu.edu/nzn/journals/2014/05/articles/06
Инновационные подходы к конструированию высокоэффективного породоразрушающего инструмента / А.Я.Третьяк, В.В.Попов, А.Н.Гроссу, К.А.Борисов // Горный информационно-аналитический бюллетень. 2017. № 8. С. 217-222. DOI: 10.25018/0236-1493-2017-8-0-225-230
Катанов Б.А. Использование стержневых резцов как разрушающего инструмента пород средней крепости / Б.А.Катанов, В.Г.Внуков // Вестник Кузбасского государственного технического университета. 2004. № 6.1. С. 29-33. URL: https://vestnik.kuzstu.ru/index.php?page=article&id=1450
Нескромных В.В. Аналитическое исследование процесса резания-скалывания горной породы долотом с резцами PDC / В.В.Нескромных, К.И.Борисов // Известия Томского политехнического университета. 2013. Т. 323. № 1. С. 191-195. URL: http://izvestiya.tpu.ru/archive/article/view/1061
Остановский А.А. Теоретические аспекты адаптивного процесса резания горных пород / А.А.Остановский, М.А.Васин // Горный информационно-аналитический бюллетень. 2014. № 2. С. 198-203. URL: https://elibrary.ru/item.asp?id=21192457
Попов С.Н. Алгоритм расчета энергии контактного взаимодействия режущего инструмента баровой машины в условиях изнашивания с закрепленным абразивом / С.Н.Попов, С.В.Андриенко // Новые материалы и технологии в металлургии и машиностроении. 2013. № 2. С. 138-146. DOI: 10.15588/.v0i2.99623 (на украинском).
Прокопенко С.А. Перспективные конструкции резцов для повышения сортности добываемого шахтами угля // Уголь. 2017. № 4. С. 29-31. DOI: 10.18796/0041-5790-2017-4-29-31
Прокопенко С.А. Повышение эффективности разрушения горных пород спаренной работой резцов с разными наконечниками / С.А.Прокопенко, М.Чехлар // Уголь. 2018. № 11. С. 18-21. DOI: 10.18796/0041-5790-2018-11-18-21
ПрокопенкоС.А. Эволюция конструкции резцов для шахтных комбайнов / С.А.Прокопенко, В.С.Лудзиш // Горная промышленность. 2015. № 2 (120). С. 65. URL: https://mining-media.ru/ru/article/podzemmash/8560-evolyutsiya-konstruktsii-reztsov-dlya-shakhtnykh-kombajnov
Пути развития теории разрушения углей и горных пород резцовым инструментом / А.Б.Жабин, А.В.Поляков, Е.А.Аверин и др. // Уголь. 2019. № 9. С. 24-28. DOI: 10.18796/0041-5790-2019-9-24-28
Пушмин П.С. Особенности механизма разрушения твердой горной породы алмазным породоразрушающим инструментом / П.С.Пушмин, Г.Р.Романов // Науки о Земле и недропользование. 2014. № 5 (48). С. 67-72. URL: http://journals.istu.edu/nzn/journals/2014/05/articles/07
Состояние научных исследований в области разрушения горных пород резцовым инструментом на рубеже веков / А.Б.Жабин, А.В.Поляков, Е.А.Аверин, В.И.Сарычев // Известия Тульского государственного университета. Науки о Земле. 2018. № 1. С. 230-247. DOI:10.24410/px6n-5y37
Сысоев Н.И. Применение метода конечных элементов для определения конструктивных параметров буровых резцов / Н.И.Сысоев, Чу Ким Хунг // Известия высших учебных заведений. Северо-Кавказский регион. Технические науки. 2015. № 4 (185). С. 73-80. DOI: 10.17213/0321-2653-2015-4-73-80
Чебан А. Ю. Экспериментальные исследования процесса разрушения породы резцами фрезерного рабочего органа // Вестник ТОГУ. 2012. № 1 (24). С.125-128. URL: https://pnu.edu.ru/vestnik/pub/articles/1663
Шемякин С.А. Аналитические теории определения сопротивлений резанию (рыхлению) мерзлых пород и их применение в практике расчета землеройной техники: монография / С.А.Шемякин, Е.А.Шишкин. Хабаровск: Изд-во Тихоокеанского государственного университета, 2014. 143 с.
Шемякин С.А. Определение сопротивления резанию мерзлых пород глубокоблокированным (щелевым) способом / С.А.Шемякин, А.Ю.Чебан // Горное оборудование и электромеханика. 2015. № 6 (115). С. 39-44.
Шемякин С.А. Технико-технологические решения разработки мерзлых пород в горном деле и строительстве: Монография / С.А.Шемякин, Ю.А.Гамоля, А.Ю.Чебан. Хабаровск: Изд-во Дальневосточного государственного университета путей сообщения, 2017. 188 с.
A theoretical model for estimating the peak cutting force of conical picks / X.Li, S.Wang, S.Ge et al. // Experimental Mechanics. 2018. Vol. 58. P. 709-720. DOI: 10.1007/s11340-017-0372-1
Bao R.H. Estimating the peak indentation force of the edge chipping of rocks using single point-attack pick // Rock mechanics and rock engineering. 2011. Vol. 44. P. 339-347. DOI: 10.1007/s00603-010-0133-2
Bilgin N. Effect of replacing disc cutters with chisel tools on performance of a TBM in difficult ground conditions / N.Bilgin, H.Copur, C.Balci // Tunnelling and underground space technology. 2012. Vol. 27. Iss. 1. P. 41-51. DOI: 10.1016/j.tust.2011.06.006
Carbonell J.M. Modelling of tunnelling processes and rock cutting tool wear with the particle finite element method (PFEM) / J.M.Carbonell, E.Onate, B.Suarez // Computational mechanics. 2013. Vol. 52. P. 607-629. DOI: 10.1007/s00466-013-0835-x
Dewangan S. Wear assessment of conical pick used in coal cutting operation / S.Dewangan, S.Chattopadhyaya, S.Hloch // Rock mechanics and rock engineering. 2015. Vol. 48. P. 2129-2139. DOI: 10.1007/s00603-014-0680-z
Dominant rock properties affecting the performance of conical picks and the comparison of some experimental and theoretical results / N.Bilgin, M.A.Demircin, H.Copur et al. // International journal of rock mechanics and mining sciences. 2006. Vol. 43. Iss. 1. P. 139-156. DOI: 10.1016/j.ijrmms.2005.04.009
Goktan N. A semi-empirical approach to cutting force prediction for point-attach picks / R.M.Goktan, N.Gunes // Journal of the southern African institute of mining and metallurgy. 2005. Vol. 105. Iss. 4. P. 257-263. URL: https://hdl.handle.net/10520/AJA0038223X_3043
Gunes Yilmaz N. Rock cuttability assessment using the concept of hybrid dynamic hardness (HDH) / N.Gunes Yilmaz, D.Tumac, R.M.Goktan // Bulletin of engineering geology and the environment. 2015. Vol. 74. P. 1363-1374. DOI: 10.1007/s10064-014-0692-7
Khair A.W. Research and innovations for continuous miner’s cutting head for efficient cutting process of rock/coal // In Proceedings of the 17th International mining congress and exhibition of Turkey, 19-22 June 2001, Ankara, Turkey. Chamber of Mining Engineers of Turkey, 2001. Vol. 17. P. 45-55. URL: https://www.maden.org.tr/resimler/ekler/52d2c9ecfe079e5_ek.pdf
Li H.S. Numerical simulation on interaction stress analysis of rock with conical picks / H.S.Li, S.Y.Liu, P.P.Xu // Tunnelling and Underground Space Technology. 2019. Vol. 85. P. 231-242. DOI: 10.1016/j.tust.2018.12.014
Li X. Hard rock cutting with SMARTCUT technology / X.Li, B.Tiryaki, P.W.Cleary // Conference: 22nd World mining congress and expo, 11-16 September 2011, Istanbul, Turkey. Chamber of Mining Engineers of Turkey, 2011. P. 725-732. DOI: 10.13140/2.1.4381.0885
Research on strength of roadheader conical picks based on finite element analysis / X. Li, Y.Lv, Q.Zeng, J.Wang // Open mechanical engineering journal. 2015. Vol. 9. P. 521-526. DOI: 10.2174/1874155X01509010521
Linear rock cutting with SMART*CUT picks / W.Shao, X.Sheng Li, Y.Sun, H.Huang // Applied mechanics and materials. 2013. Vol. 477-478. P. 1378-1384. DOI: 10.4028/www.scientific.net/AMM.477-478.1378
Mechatronic model of continuous miner cutting drum driveline / A.Mezyk, W.Klein, M.Fice et al. // Mechatronics. 2015. Vol. 37. P. 12-20. DOI: 10.1016/j.mechatronics.2015.11.004
Prakash A. A new rock cuttability index for predicting key performance indicators of surface miners / A.Prakash, M.Vemavarapu, K.B.Singh // International journal of rock mechanics and mining sciences. 2015. Vol. 77. P. 339-347. DOI: 10.1016/j.ijrmms.2015.04.016
Prediction of tool forces in rock cutting using discrete element method / Z.Qianqian, H.Zhennan, Z.Mengqi, Z.Jianguang // Electronic journal of geotechnical engineering. 2015. Vol. 20(5). P. 1607-1625. URL: https://web.archive.org/web/20180428025710id_/http://www.ejge.com/2015/Ppr2015.0182ma.pdf
Discrete element modelling of rock cutting / J.Rojek, E.Oñate, C.Labra, H.Kargl // Particle-based methods. 2011. P. 247-267. DOI: 10.1007/978-94-007-0735-1_10
Su O. Modeling of cutting forces acting on a conical pick / O.Su, N.A.Akcin, L.te Kamp // Proceeding of EURO: TUN 2009 II International conference on computational methods in tunneling, 9-11 September 2009, Bochum, Germany. Aedificatio Publishers, 2009. P. 1-8. URL: https://www.researchgate.net/profile/Okan-Su/publication/272337906_Modeling_of_cutting_forces_acting_on_a_conical_pick/links/57630bec08ae192f513e3e6f/Modeling-of-cutting-forces-acting-on-a-conical-pick.pdf
Su O. Numerical simulation of rock cutting using the discrete element method / O.Su, N.Ali Akcin // International journal of rock mechanics and mining sciences. 2011. Vol. 48. Iss. 3. P. 434-442. DOI: 10.1016/j.ijrmms.2010.08.012
Wang S. Analysis of rockburst triggered by hard rock fragmentation using a conical pick under high uniaxial stress / S.Wang, L.Huang, X.Li // Tunnelling and Underground Space Technology. 2020 Vol. 96. № 103195. DOI: 10.1016/j.tust.2019.103195
Wang X. Specific energy analysis of rock cutting based on fracture mechanics: a case study using a conical pick on sandstone / X.Wang, O.Su // Engineering fracture mechanics. 2019. Vol. 213. P. 197-205. DOI: 10.1016/j.engfracmech.2019.04.010
Yasar S. Predictive plots for conical pick performance using mechanical and elastoplastic properties of rocks // Journal of rock mechanics and geotechnical engineering. 2020. Vol. 12. Iss. 5. P. 1027-1035. DOI: 10.1016/j.jrmge.2019.12.020
Yilmaz N.G. Prediction of radial bit cutting force in high-strength rocks using multiple linear regression analysis / N.G.Yilmaz, M.Yurdakul, R.M.Goktan // International journal of rock mechanics and mining sciences. 2007. Vol. 44. Iss. 6. P. 962-970. DOI: 10.1016/j.ijrmms.2007.02.0