Динамическое моделирование промышленного цикла кристаллизации гиббсита
- 1 — канд. техн. наук начальник отдела РУСАЛ Инженерно-технологический центр ▪ Orcid ▪ Elibrary ▪ Scopus
- 2 — д-р техн. наук профессор Санкт-Петербургский горный университет ▪ Orcid ▪ Elibrary ▪ Scopus ▪ ResearcherID
Аннотация
Модель популяционного баланса критически важна для улучшения способа массовой кристаллизации гидроксида алюминия и повышения качества управления промышленными нитками декомпозиции. В работе представлена обновленная модель популяционного баланса, которая может использоваться для моделирования декомпозиции в промышленном масштабе. Процессы рождения с распространением и разрушением частиц рассмотрены в качестве неотъемлемых составляющих декомпозиции наряду с вторичным зародышеобразованием, ростом и агломерацией частиц. Принципиальным отличием предложенной системы уравнений стала возможность воспроизведения ею колебательного процесса, возникающего в циклах декомпозиции в результате циклического изменения качества затравочной поверхности. Показана возможность возникновения в такой системе автоколебаний без внешнего воздействия. Улучшенная модель настроена и проверена с помощью архивных промышленных данных. Продемонстрировано точное совпадение рассчитанной динамики изменения фракционного состава гидроксида алюминия с практическими данными при моделировании промышленного цикла декомпозиции с оборотом затравки.
Введение
Теория массовой кристаллизации гидроксида алюминия из пересыщенного алюминатного раствора на затравке широко представлена в литературе. В зависимости от состава раствора, температуры и присутствия модификаторов роста или добавок кристаллизация гидроксида алюминия может протекать в форме байерита, гиббсита, бемита и аморфной фазы. В условиях байеровского процесса формирование кристаллов гидроксида алюминия занимает от нескольких дней до нескольких месяцев. Промышленная декомпозиция протекает при разных температурах и пересыщениях в батарее декомпозеров.
Известны уравнения, описывающие скорость линейного роста кристаллов, их агломерацию, вторичное зародышеобразование и разрушение [11, 19, 21, 27]. Широко применяется уравнение популяционного баланса кристаллов в процессе декомпозиции, для решения которого предложено несколько способов [4, 10, 14]. Для циклов декомпозиции созданы надежные математические описания аппаратов: классификаторов, гидроциклонов, фильтров, мешалок [18, 20, 22]. Усилиями программистов из этого набора формул легко формируется единая система уравнений, решаемая методами моделирования химико-технологических систем [24, 25]. Предложены методы настройки уравнения популяционного баланса и его составляющих, выполнено много модельных исследований для условий периодического и полупериодического опытов без оборота затравки [9, 13, 16]. Однако перечисленные методы ограниченно применимы для описания результатов промышленной декомпозиции с оборотом затравки и прогнозирования ее развития в динамике. Проблема в том, что известные модели роста, агломерации и зародышеобразования чрезмерно консервативны. При их использовании в результатах моделирования наблюдается быстрое затухание колебаний с выходом на стационарное состояние, что не совпадает с заводскими наблюдениями [5].
В данной работе объяснены причины возникновения динамических волн изменения фракционного состава и продуктивности раствора и предпринята попытка доработки уравнений модели популяционного баланса, чтобы с их помощью появилась возможность моделирования динамических изменений в промышленных циклах декомпозиции с оборотом затравки гидроксида алюминия.
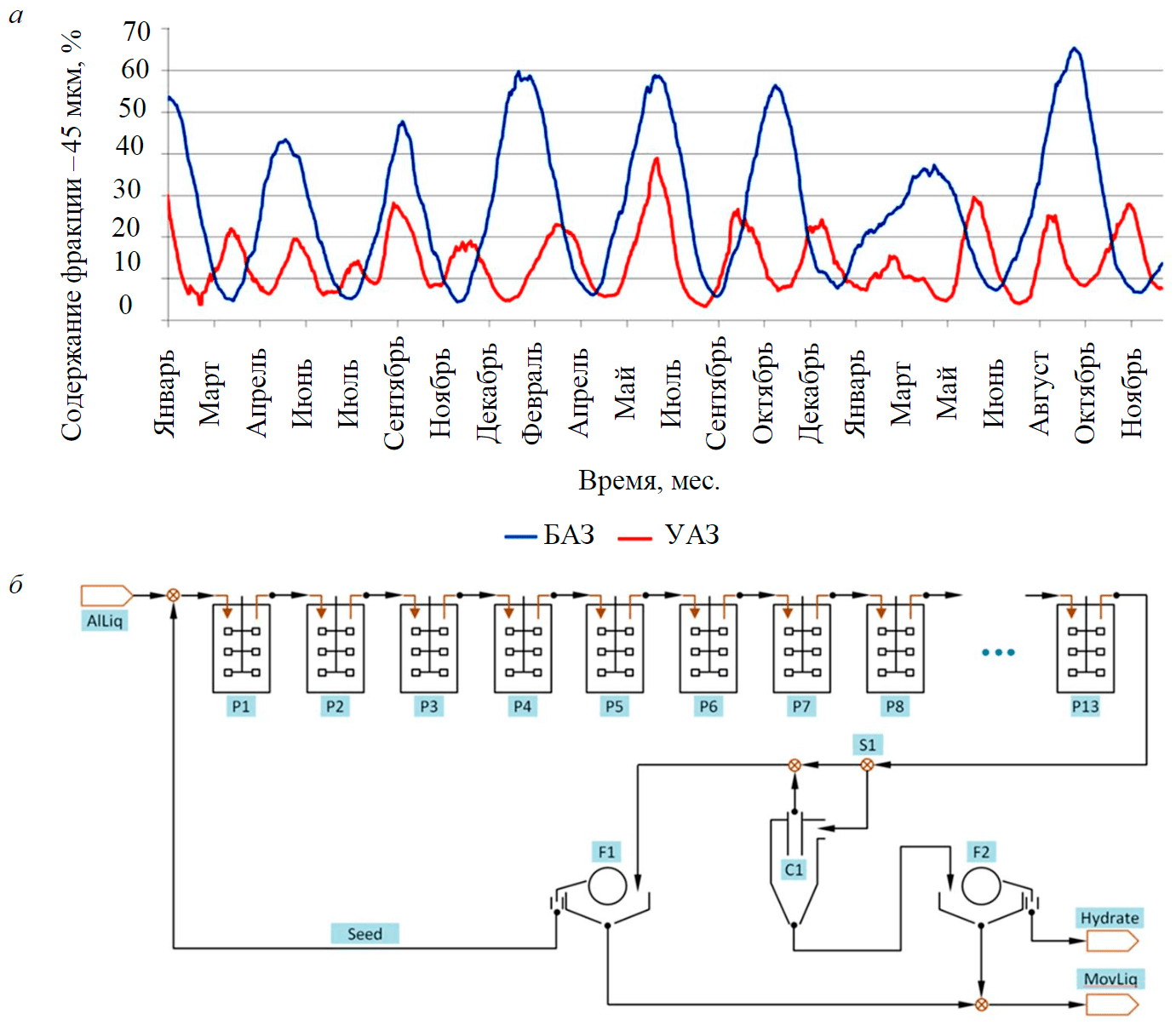
Рис.1. Изменение содержания класса –45 мкм в затравке ниток декомпозиции Богословского и Уральского алюминиевых заводов в течение 3 лет (а), принципиальная схема нитки разложения алюминатного раствора на УАЗе (б)
Методология
Промышленные данные. Характерным примером значительной нестабильности свойств затравки и продуктивности раствора являются системы, не имеющие условий для активной агломерации мелких кристаллов при декомпозиции. Колебательный процесс в таких системах принимает опасные масштабы и в определенные периоды создает угрозу получения глинозема, крупность которого не соответствует сертификату.
Промышленные данные (рис.1, а) характеризуют режим работы участков декомпозиции двух глиноземных заводов, расположенных в РФ: Уральского (УАЗ) и Богословского (БАЗ) алюминиевых заводов. На графике показана динамика изменения содержания фракции –45 мкм и явно прослеживаются регулярные колебания фракционного состава с периодом 2-3 мес. на БАЗ и 1-2 мес. на УАЗ. Амплитуда наблюдаемых осцилляций изменяется, их период достаточно регулярен, и наступление очередного экстремума представляется неизбежным.
Оба предприятия перерабатывают бемит-диаспоровые бокситы, используют среднетемпературное выщелачивание без подслащения. Алюминатный раствор поступает на декомпозицию с концентрацией каустической щелочи 240-260 г/л по Na2CO3 и разлагается при начальном отношении A/C = 0,55-0,57 до 0,28-0,31. Агломерация мелкой затравки происходит малоэффективно, поэтому управление режимом декомпозиции сводится к изменению температуры головного и хвостового декомпозеров, а также (для УАЗа) – к смене конусов продукционных гидроциклонов.
Одной из важнейших задач при таком подходе к управлению является оценка наилучшего момента и уровня воздействия, чтобы управление происходило в противофазе к естественному ходу процесса и было адекватно по величине.
Посредством стандартных методов (микроскопных наблюдений и лазерного анализа размера частиц) удается зафиксировать уже начавшееся укрупнение или измельчение. Попытки действовать на упреждение еще до появления инструментальных признаков начала измельчения или укрупнения на практике нередко заканчивались потерей контроля над процессом. В этом случае пики содержания класса –45 мкм в конце фазы укрупнения достигали 1-3 %, а в фазе измельчения доходили до 60-70 %. В моменты значительного укрупнения производительность участка могла снижаться в 1,5 раза.
Наблюдения за изменением содержания отдельных классов частиц, производительностью, составом раствора, температурным и концентрационным режимом декомпозиции на УАЗ и БАЗ ведутся на протяжении 15 лет, параметры процесса фиксируются ежедневно. Они составляют достаточный объем данных для изучения кристаллизации гиббсита в промышленных условиях и проверки методов моделирования. Значительные колебания, зафиксированные в ходе наблюдений, оказались крайне полезны для исследования.
В качестве основного объекта исследований выбран передел декомпозиции на УАЗе. Завод имеет несколько ниток декомпозиции разного объема, но принципиальная схема их устройства одинакова (рис.1, б). Декомпозиция раствора протекает в одну стадию. В качестве классификаторов применяются батареи гидроциклонов. Классификации подвергается только часть потока пульпы с целью выделения из нее крупных классов. Продукционный гидрат, представленный песками гидроциклонов, фильтруется вакуумными фильтрами и направляется на промывку. Основная часть потока пульпы из последнего декомпозера, байпасом минуя гидроциклоны, совместно с их сливом направляется на узел затравочной фильтрации.
Модель популяционного баланса. Базовыми уравнениями, использованными в исследовании, стали уравнения популяционного и материального балансов, которые связывают степень разложения алюминатного раствора с изменением характеристик семейства кристаллов гидроксида алюминия [21]:
где ni – число частиц в i-м классе; Li – размер i-го класса, м; $\frac{\delta n_i}{\delta t}$ – скорость изменения числа частиц в классе размера u во времени в единице объема пульпы, 1/(м4∙с); G – линейная скорость роста кристаллов, м/с; Bi, Di – скорость появления и исчезновения частиц в i-м классе в результате их создания и перехода между классами соответственно, 1/(м4∙с); A – концентрация Al2O3 в растворе, г/л; M[Al2O3], M[Al(OH)3] молярная масса Al2O3 и Al(OH)3 соответственно, кг/моль; ρА – плотность гидроксида алюминия, кг/м3.
Модели роста и агломерации. Уравнения (1)-(2) решаются совместно с использующимися в подобных исследованиях выражениями скорости линейного роста и агломерации кристаллов:
- модель скорости линейного роста частиц, независимой от размера частиц [27],
где k0 – предэкспоненциальный множитель константы скорости линейного роста; Eact – энергия активации реакции, Дж/моль; T – температура, К; Aeq – равновесная концентрация глинозема в растворе, г/л; z1 – показатель степени при пересыщении; С – концентрация каустической щелочи Na2CO3, г/л;
- модель агломерации с функцией вероятности, зависимой от размера частиц, может быть сформулирована для каждого класса частиц следующим образом [11, 15]:
где v,u – координаты класса частиц в дисперсии; n – количество частиц в единице объема; β(v,u) – функция, выражающая вероятность агломерации частиц размера v и u (ядро агломерации); kc – коэффициент пропорциональности в модели агломерации; β4 – поправка, учитывающая условия агитации в декомпозере.
Первое слагаемое в формуле (4) описывает прирост частиц внутри рассматриваемого класса v за счет агломерации частиц меньших классов (0-v), а второе слагаемое отвечает за уменьшение числа частиц в рассматриваемом классе за счет связывания в агломераты с частицами других классов.
Модель вторичного зародышеобразования. Скорость вторичного зародышеобразования (1/м3∙с) чаще всего рассчитывают при постоянной скорости образования зародышей на единицу поверхности раздела фаз [19]:
где kn – настраиваемая константа скорости зародышеобразования, 1/(м3с); Ssl – площадь поверхности раздела фаз в единице объема пульпы, 1/м; z2 – показатель степени при пересыщении, причем в работе [19] z2 = 2.
Модель разрушения. Разрушение частиц обычно связывают с их истиранием и раскалыванием. Истирание приводит к незначительному изменению размера исходной частицы и образованию новых частиц размера, близкого к размеру зародышей. В этом понимании истирание эквивалентно контактному зародышеобразованию. Под разрушением понимается только акт раскалывания частицы с образованием двух новых одинаковых частиц – бинарное разрушение. Функция разрушения может быть записана подобно модели агломерации для каждого класса частиц [3]:
где ϑ(t, u) – функция вероятности разрушения частиц в классе u; первое слагаемое в правой части уравнения (7) отвечает за появление частиц класса u при разрушении более крупных частиц, а второе слагаемое – за разрушение частиц класса u.
Упрощение уравнения (7) для бинарного разрушения дает
Вероятность разрушения частиц может быть выражена степенной зависимостью [23]
где kb и p – настраиваемые константы, через которые учитывается соотношение сдвиговых сил в жидкости и внутренних сил сцепления в частицах; ϒ – скорость сдвига, с–1; $\overline{m}$ – нормализованный первый момент популяции кристаллов в единице объема, 1/м2.
Модель гидроциклона. Для замыкания материального баланса декомпозиции по контуру классификации затравки применена модель гидроциклона, предложенная Нагесварарао [20]. С ее помощью определяется классификационный размер гидроциклона:
где KD0 – коэффициент коррекции d50; Dc, Di, Do, Du – диаметр циклона, входа, трубы слива гидроциклона и песковой насадки соответственно, м; Lc – длина цилиндрической части гидроциклона, м; H – гидравлический уклон, м; θ – центральный угол конусной части гидроциклона, градус; λ – коэффициент равнопадаемости при стесненном падении по хиндереру, рассчитывающийся по формуле
где CV – объемная доля твердой фазы в пульпе на входе в гидроциклон.
Расчет доли жидкости, выходящей через конус гидроциклона, выполняется по формуле:
где Kw0 – коэффициент коррекции.
Фракционная эффективность улавливания частиц рассчитывалась по уравнению Уайтена [2]:
где α, ω, ω* – настраиваемые константы.
Природа осцилляций. Существуют разные объяснения регулярных колебаний фракционного состава в циклах декомпозиции с оборотом затравки. Одни исследователи указывают на хаотичность процесса и фрактальное строение частиц [28], другие связывают колебания с классификаторами гидрата, которые способны вызывать осцилляции фракционного состава вследствие накопления в них гидроксида алюминия, количество которого сопоставимо с массой твердого, находящегося в декомпозерах [6]. Данный случай, известный в теории автоматизированного управления как транспортное запаздывание, при определенных условиях способен вызывать колебания в системе, в том числе незатухающие. Однако это не объясняет возникновение сильного колебательного процесса в циклах кристаллизации УАЗа, где классификаторы затравки не применяются, и БАЗа, где классификация гидроксида алюминия отсутствует совсем.
В условиях промышленного предприятия изменения фракционного состава также вызываются пульсациями расхода, концентрацией и модулем алюминатного раствора, содержанием растворенных в нем примесей [12], изменением суточной температуры окружающего воздуха, плановыми ремонтами и остановками, большим числом других хаотических факторов. Тем не менее, ни один из них не способен объяснить периодичность, регулярность и амплитуду основной моды колебаний, наблюдаемых на рис.1, а.
Частой рекомендацией по управлению процессом зародышеобразования является контроль и поддержание стабильного отношения абсолютного пересыщения к полной поверхности затравки DС/Ssl [26]. Проведенный статистический анализ промышленных данных УАЗа и БАЗа показал, что корреляционная связь между скоростью изменения фракционного состава и отношением пересыщения к полной поверхности затравки ΔС/Ssl крайне слаба (коэффициент детерминации R2 менее 0,1). Поэтому для указанных заводов рекомендация не актуальна.
В качестве рабочей гипотезы о природе осцилляций в данном исследовании сделано предположение, что источник возбуждения самой длинной волны изменения фракционного состава имеет естественную природу и связан со свойствами поверхности затравки. Это допущение соответствует общепризнанным представлениям о том, что моментом начала активного выхода зародышей в раствор является снижение численной плотности центров линейного роста на поверхности кристалла [7].
Модель рождения с распространением. Согласно теории кристаллизации процессы роста и зародышеобразования имеют общее начало, заключающееся в адсорбции молекулы на поверхности частицы с частичной потерей сольватной оболочки (рис.2, а). Первичное закрепление молекулы происходит на плоской, энергетически наименее выгодной поверхности частицы (рис.2, б). Затем происходит миграция сорбированной молекулы по поверхности, сопровождающаяся преодолением энергетических барьеров 3 и 5 в более выгодные места закрепления 4 и 6 [7].
В случае невозможности преодоления пути 3 созревание зародыша с присоединением к нему новых молекул будет происходить на плоской поверхности, при этом связь данной группы молекул с основой наименее прочна, и последующий отрыв такого зародыша под действием внешней механической силы наиболее вероятен.
С учетом приведенного механизма процесс адсорбции первичных зародышей на поверхности затравки не зависит от качества поверхности и определяется только ее площадью, коэффициентом диффузии, толщиной диффузионного слоя и пересыщением раствора. Толщину диффузионного слоя можно считать условно постоянной при неизменной скорости агитации. Коэффициент диффузии по формуле Стокса – Эйнштейна зависит от температуры, но учитывать его влияние отдельно не требуется, поскольку в ходе настройки показателя степени при пересыщении это влияние в первом приближении может быть учтено. Таким образом, для расчета скорости адсорбции первичных зародышей на поверхности затравки без доработки можно использовать уравнение (6), предложенное для вторичного зародышеобразования.
Энергетические затраты на преодоление первичным зародышем путей 3 и 5 (рис.2, а, б) характеризуют вероятность его перехода в раствор. В случае сокращения этих путей, в первую очередь за счет образования агломератов, повышающих фрактальность поверхности и приводящих к появлению у кристалла множественных точек роста, вероятность закрепления первичных зародышей на поверхности затравки растет, а обратная ей вероятность выхода вторичных зародышей в раствор снижается.
По мере укрупнения и идеализации формы частицы эти пути удлиняются, закрепление зародыша в точках роста родительской частицы ухудшается, у него появляется больше шансов сформировать собственный центр роста и в виде вторичного зародыша выйти в раствор.
Рождение с распространением предлагается описывать как двустадийный процесс, в ходе которого первичный зародыш образуется на поверхности, а затем срастается с частицей при наличии рядом с местом закрепления подходящих вакансий (рис.2, в). Скорость процесса пропорциональна произведению двух вероятностей: вероятности абсорбции первичного зародыша на поверхности затравки и вероятности его прочного соединения с поверхностью. С учетом этого выражение для скорости рождения с распространением примет такой вид:
или
где k1 – безразмерный коэффициент, учитывающий прочие факторы; Nv/Ne = nv – число доступных вакансий для одного зародыша; µi=nv/Sf – численная плотность доступных вакансий на единице поверхности частицы, 1/м2; $\sum_i(S_{fi}\mu_i)$ – средняя вакантность поверхности во всей популяции частиц.
Численная плотность доступных вакансий µi является выражением качества затравочной поверхности.
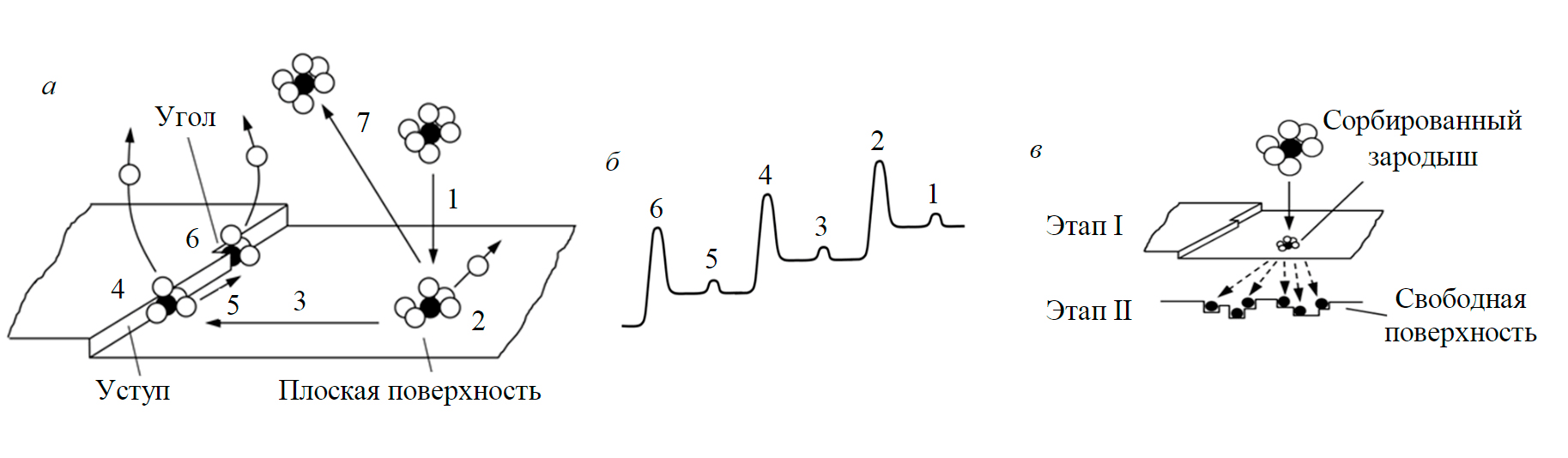
Рис.2. Энергетика роста кристаллов из раствора: движение сольватированной молекулы растворенного вещества (а); whereсоответствующие изменения энергии для каждого преобразования [8] (б); последовательность связывания зародышей whereс поверхностью в результате рождения с распространением(в)
Она снижается в результате длительного роста частицы и возрастает в ходе агломерации. Следовательно, для популяции частиц, в которой преобладают агломераты, она будет больше, чем для популяции, в которой доля агломератов незначительна. Таким образом можно связать долю агломератов с численной плотностью вакансий. Чтобы не оперировать абсолютными значениями числа вакансий, необходимо перейти к относительным величинам:
где µa и µg – численная плотность доступных вакансий у агломератов и ростовых частиц соответственно, 1/м2; fa и fg – доля агломератов и ростовых частиц соответственно; $\mu_a/\mu_g=\mu^- $ – величина, выражающая превышение вероятности связи зародыша с поверхностью у агломерата по сравнению с ростовой частицей.
Если принять, что величина постоянна, то выражение (15) для скорости процесса рождения с распространением с учетом формулы (16) можно переписать в таком виде:
где ks = k1μg – настраиваемая константа.
Доля агломератов fa – понятие условное, так как одна и та же частица может быть только что сформированным агломератом двух частиц или агломератом, который длительное время продолжал свой рост как единая частица. Для единства подхода предлагается принять правило, что частицы делятся на агломераты и не агломераты в момент их перехода между классами. Это позволит на каждой итерации вычислений при появлении в классе новых частиц фиксировать их тип и рассчитывать новую долю агломератов в классе. Если частица в рассмотренном классе возникла в результате зародышеобразования, линейного роста или разрушения, она относится к обычным частицам; если ее появление связано с актом агломерации – причисляется к агломератам.
Обсуждение
Обновленная модель зародышеобразования. Принимая во внимание конкуренцию между процессами вторичного зародышеобразования и рождения с распространением, с учетом формул (6) и (17), выражение для скорости выхода зародышей в раствор можно сформулировать в таком виде:
или
где B0 – число зародышей, поступивших в раствор,1/(м3×с); BM – полная скорость зародышеобразования на поверхности частицы, рассчитываемая по формуле (6),1/(м3×с); BS – скорость процесса рождения с распространением, 1/(м3×с); BM/BD – отношение скоростей процессов вторичного зародышеобразования на поверхности частицы и рождения с распространением.
Параметры kn, ks и в формуле (19) подбираются при настройке модели в динамическом режиме, воспроизводя реально возникающие осцилляции фракционного состава.
Обновленная модель разрушения. В уравнении (8) была принята бинарная схема разрушения частиц. Чтобы в условиях этой схемы учесть возможность многократных последовательных разрушений, необходимо ввести функцию вероятности разрушения для частиц разных фракций. В этом качестве в исследовании была использована функция Гаусса, пик которой соответствует размеру наиболее разрушаемых частиц,
где F(u) – интенсивность разрушения частиц класса u, 1/(м3×с); – размер наиболее разрушаемых частиц, м.
В присутствии большого количества примесей послойный линейный рост частиц затруднен, что ведет к образованию частиц неправильной формы и отростков, плохо связанных с основой и склонных к скалыванию. Такие частицы появляются в период активной агломерации, особенно если она происходит при низких температурах. Подобно модели рождения с распространением, для учета интенсивности разрушения частиц в каждом классе можно также использовать долю агломератов fa(t, u). При дополнении уравнения вероятности разрушения частиц (9) новыми свойствами получается равенство
Таким образом, предлагаемая улучшенная модель разрушения состоит из уравнений (8), (20) и (21).
Признаки колебательного процесса. Представленные уравнения, включающие модель агломерации (4)-(5), улучшенную модель зародышеобразования (19) и улучшенную модель разрушения (8), (20) и (21), могут быть упрощены и сгруппированы в отдельную подсистему обыкновенных дифференциальных уравнений:
где
где $ N^{.}_{g.n},N^{.}_{g.a}, N^{.}_{g.b}$ – члены, выражающие скорость изменения числа ростовых частиц в результате зародышеобразования, агломерации и разрушения соответственно; $N^{.}_{g.b},N^{.}_{a.a}, N^{.}_{a.b}$ – члены, выражающие скорость изменения числа агломератов в результате зародышеобразования, агломерации и разрушения соответственно; $N_{g}(t),N_{a}(t)$ – число ростовых частиц и агломератов соответственно; $f_a=N_a(t)/[N_g(t)+N_a(t)]$ – доля агломератов в популяции; $N_g(t)+ N_a(t)$ – упрощение для полной поверхности частиц Ssl из формулы (19); $k_{n1}, k_{n2}, \phi, k_{ga},k_{gg},k_{aa}, k_{b}$ – постоянные коэффициенты.
Система уравнений (22)-(27) решается при начальных условиях $ dN_g(0)=n_g$ и $ dN_a(0)=n_a$. Из системы уравнений были исключены источники и стоки массы, свойства раствора приняты неизменными, рост частиц не учитывается. При этих условиях появляется возможность исследовать систему на предмет автоколебаний только относительно свойств затравочной поверхности.
С определенным набором значений (например kn1 = 0,07; kn2 = 0,8; φ = 3,33; kga = 8×10–4, kgg = 6×10–3; kgg = 8×10–4; kb = 0,001; ng = 0,01; na = 0,01) при решении системы уравнений (22)-(27) появляются незатухающие автоколебания (рис.3). При иных сочетаниях параметров колебательный процесс может прийти к стационарному состоянию. С исключением из системы любого слагаемого автоколебания прекращаются.
Структура системы уравнений (22)-(27) близка к известной модели «хищник – жертва» Лотки – Вольтерры [17], только в ходе декомпозиции конкуренция происходит между ростовыми частицами и агломератами в результате процессов вторичного зародышеобразования, рождения с распространением, агломерации и разрушения.
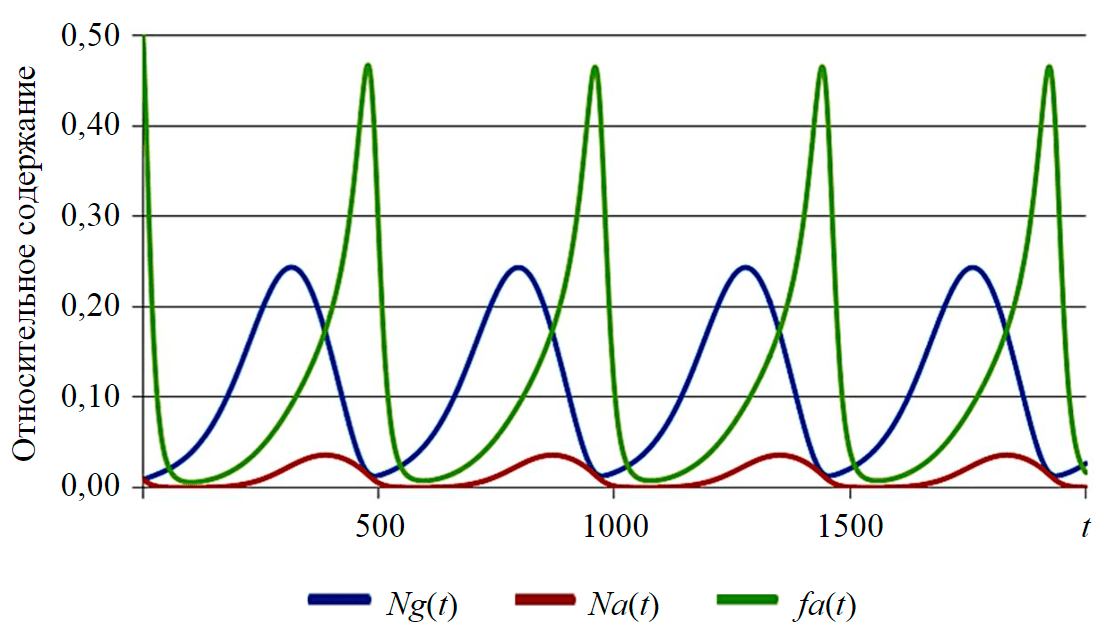
Рис.3. Автоколебательный процесс при декомпозиции в замкнутой системе Ng(t) – ростовые частицы; Na(t) – агломераты; fa(t) – доля агломератов
Численное моделирование. Численное моделирование выполнено в программе PrecipExpert, в которую была интегрирована разработанная модель [1]. Программа позволяет создавать схемы промышленной декомпозиции из отдельных блоков, размещая их на рабочем листе и соединяя в требуемой последовательности. Решение системы уравнений популяционного баланса производится дискретным методом [10, 14].
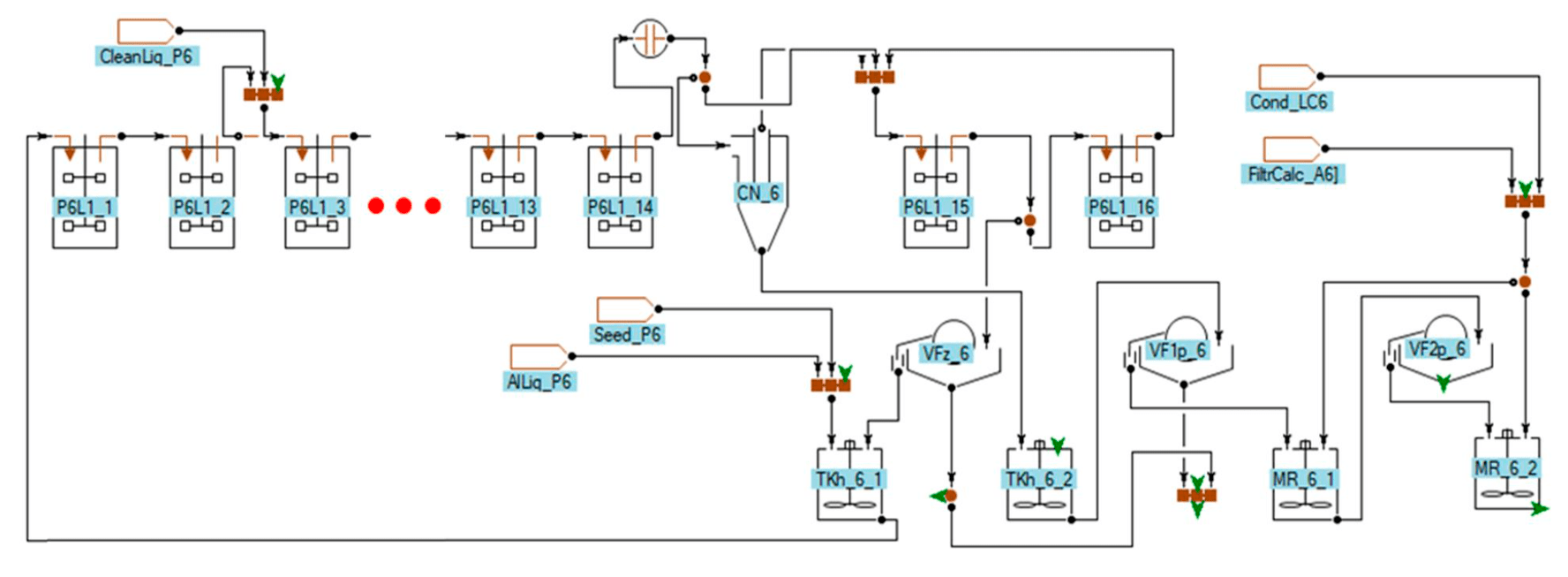
Рис.4. Схема промышленной нитки декомпозиции, использованная при моделировании
Практические расчеты были выполнены для схемы декомпозиции, изображенной на рис.4. Она состоит из 16 декомпозеров P6L1_1-P6L1_16 объемом 3500 м3, батареи гидроциклонов CN_6, фильтра затравки VFz_6, фильтра для отделения продукции VF1p_6, фильтра первой ступени промывки VF2p_6 и мешалок. Подача алюминатного раствора и собственной затравки происходит в мешалку TKh_6_1, сюда же поступает поток затравки с другой нитки декомпозиции. Дополнительно учтен поток раствора и мелкодисперсного гидроксида алюминия CleanLiq_P6, образующийся при химической чистке декомпозеров.
Для настройки и прогнозирования были выбраны разные периоды работы нитки декомпозиции. Исходные данные были взяты из архивной базы данных предприятия и дополнительных отчетов, они динамически загружались в модель. Обновление исходных данных происходило один раз в сутки, использовались значения, усредненные за сутки. Подготовка исходных данных состояла только в отсечении сильных выбросов, сглаживание данных не применялось. В составе исходных данных в модель загружались следующие параметры: расход и состав алюминатного раствора, концентрация твердого в головном декомпозере, температура в декомпозерах, количество работающих гидроциклонов, диаметры конусных насадок гидроциклонов, поток дополнительной затравки с другой нитки декомпозиции, объемы и составы растворов, вводимые после чистки декомпозеров.
Данные о фракционном составе гидроксида алюминия были переданы в динамический расчет лишь однажды – при его старте. За этим следовал непродолжительный период самонастройки модели. Во все остальное время фракционный состав гидроксида алюминия в каждом декомпозере и узле вычислялся моделью так же, как и состав растворов во всех промежуточных и выходных потоках.
Решение системы уравнений популяционного баланса выполнялось на сетке, состоящей из 30 классов:
Период обмена потоками между аппаратами (внешняя транспортная задача) составлял 10 мин, модель популяционного баланса решалась с временным шагом 150 с. Время выполнения одного динамического расчета продолжительностью 1,5 года составляло около 8 часов на CPU с производительностью 133 гигафлопса.
Настройка модели выполнена в два этапа. На первом этапе в стационарных условиях подобраны коэффициенты моделей роста, агломерации и разрушения при средних значениях всех входных параметров. В модели роста (3) параметр k0 настроен так, чтобы расчетный модуль маточного раствора при выходе процесса на стационарное состояние соответствовал среднему значению за период наблюдений. Аналогично средние значения по содержанию классов частиц –1, –5, –20, –45 мкм настроены подбором коэффициентов kс в формуле (5), δ в формуле (20), kb и p в формуле (21). Содержания наиболее крупных классов +100 и +125 мкм были настроены путем изменения параметров гидроциклона и кривой фракционной эффективности улавливания частиц (10)-(13).
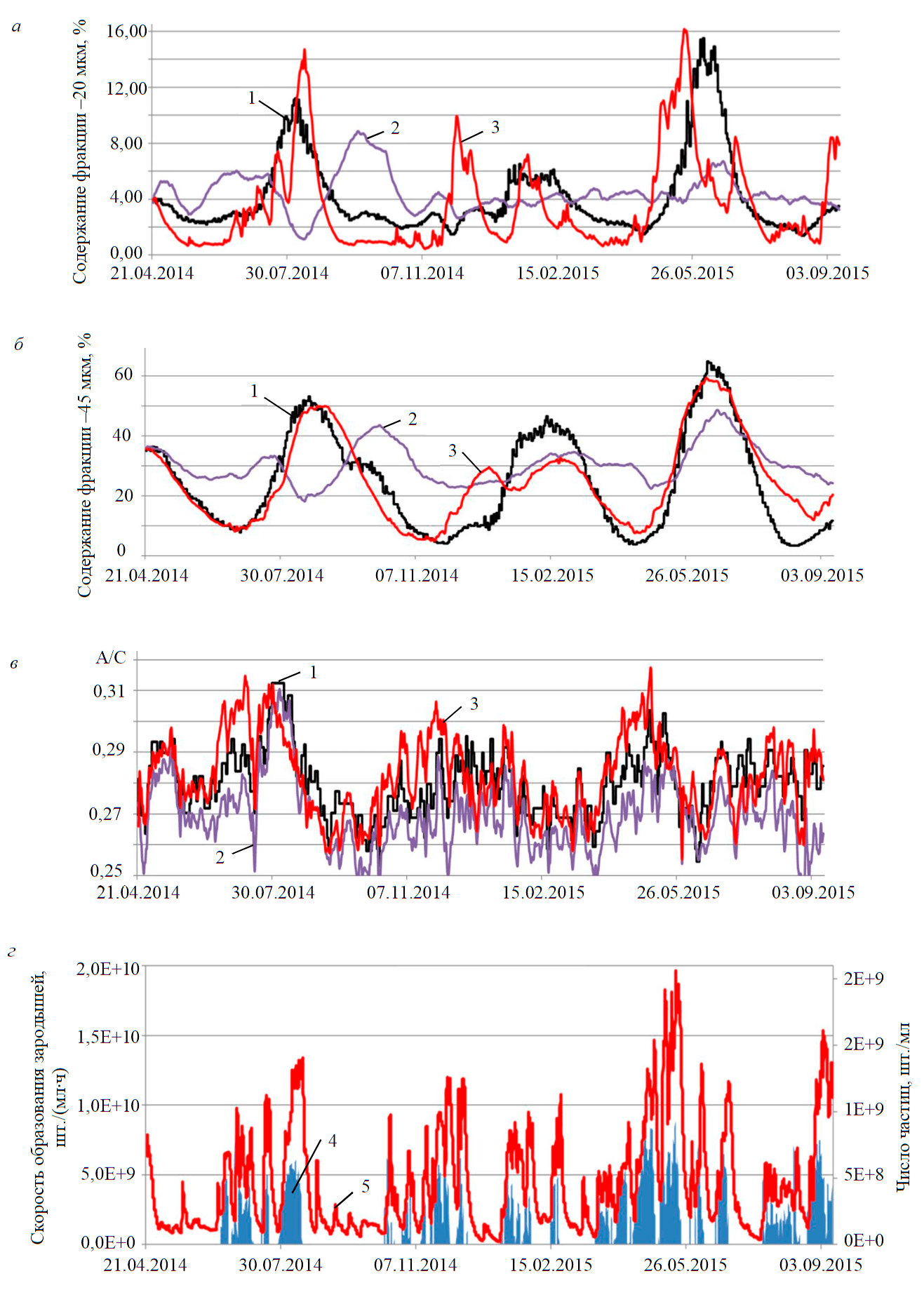
Рис.5. Результаты моделирования промышленного цикла декомпозиции гидроксида алюминия в динамическом режиме: содержание класса –20 мкм (а); –45 мкм (б) в хвостовом декомпозере; молярное отношение A/C оборотного раствора (в); рассчитанная скорость вторичного зародышеобразования и популяция кристаллов в объеме пульпы (г) 1 – эксперимент; 2 – исходная модель; 3 – улучшенная модель; 4 – скорость образования зародышей; 5 – число частиц
Второй этап настройки модели заключался в подборе коэффициентов kn, ks и в формуле (19) в динамическом режиме. Выполнялось несколько параллельных расчетов с разными значениями коэффициентов. Оптимальные значения коэффициентов найдены в результате сопоставления расчетных кривых изменения содержания классов с производственными данными. Для количественных оценок качества симуляций использовался метод наименьших квадратов. По результатам настройки получен следующий набор значений коэффициентов модели: kn = 330; Eact = 6,32×105; z1 = 4; ks = 0,61; kb = 0,95; p = 1; μ- = 3,33; δ= 2,5; kn = 1×1014; z2 = 2; ks = 12.
Качественная настройка была выполнена и для исходной модели, в которой зародышеобразование описывалось формулой (6), а разрушение – формулами (8) и (9).
Результаты
Исходная модель популяционного баланса декомпозиции и она же с предложенными доработками – заменой модели зародышеобразования (6) на (19), модели разрушения (9) на (21) с дополнением в виде уравнения (20) – были решены при одних и тех же начальных условиях и переменных среды. Продолжительность периода симуляции составила 17 месяцев. За это время зарегистрировано три полных цикла изменения фракционного состава.
Рассчитанная по моделям динамика изменения двух наиболее важных классов частиц –20 и –45 мкм в сравнении с производственными данными представлена на рис.5, а, б. В рассмотренный период времени помимо трех явных максимумов и четырех минимумов в содержании основных фракций наблюдалось большое число мелких колебаний, которые объясняются изменением внешних факторов. Эти факторы существенно отразились на результатах обоих расчетов. Прогноз, построенный исходной моделью, неудовлетворителен. Расчетная и фактическая волны не совпадают по фазе, а амплитуда спрогнозированных колебаний меньше фактической примерно в 2 раза. Обновленной моделью динамика изменения фракционного состава воспроизведена значительно более качественно. Для практического применения важно, что обновленная модель достаточно точно предсказывает моменты наступления пиков крупности и их амплитуду. В таблице представлена подробная статистика качества симуляций.
Качество симуляций
|
Параметр |
Исходная модель |
Улучшенная модель |
||
|
Коэффициент корреляции |
СКО, % |
Коэффициент корреляции |
СКО, % |
|
|
Отклонение по величине пиковых содержаний класса –45 мкм: |
|
|
|
|
|
фаза укрупнения |
–0,21 |
17,5 |
0,65 |
1,55 |
|
фаза измельчения |
0,55 |
19,7 |
0,97 |
7,75 |
|
Содержание фракции, мкм: |
|
|
|
|
|
–5 |
0,06 |
0,82 |
0,14 |
0,94 |
|
–10 |
–0,10 |
0,69 |
0,27 |
1,21 |
|
–20 |
–0,02 |
2,37 |
0,53 |
2,24 |
|
–30 |
0,16 |
7,00 |
0,80 |
3,47 |
|
–45 |
0,21 |
14,0 |
0,78 |
6,06 |
|
–63 |
0,60 |
17,1 |
0,85 |
9,22 |
|
+100 |
0,55 |
9,6 |
0,80 |
6,85 |
|
+125 |
0,58 |
4,95 |
0,83 |
4,24 |
|
A/C маточного раствора |
0,86 |
0,011 |
0,68 |
0,008 |
Отклонение по дате пика фазы укрупнения – 3 сут., фазы измельчения – 7 сут.
Заметные расхождения между расчетом по новdой модели и практикой в содержании фракции –45 мкм в январе и сентябре 2015 г. объясняются тем, что перед этими двумя периодами на систему было оказано сильное внешнее воздействие – концентрация затравки в пульпе в течение 1-2 дней была резко снижена с 820-850 до 450-500 г/л. После этого в процесс вводилась мелкая затравка с другого участка декомпозиции, которая по условию задачи не содержит агломератов. Модель отреагировала на эти воздействия последовательным снижением скорости разрушения частиц, повышением содержания агломератов, ростом вторичного зародышеобразования и, как следствие, сокращением выхода в раствор новых зародышей (рис.5, г).
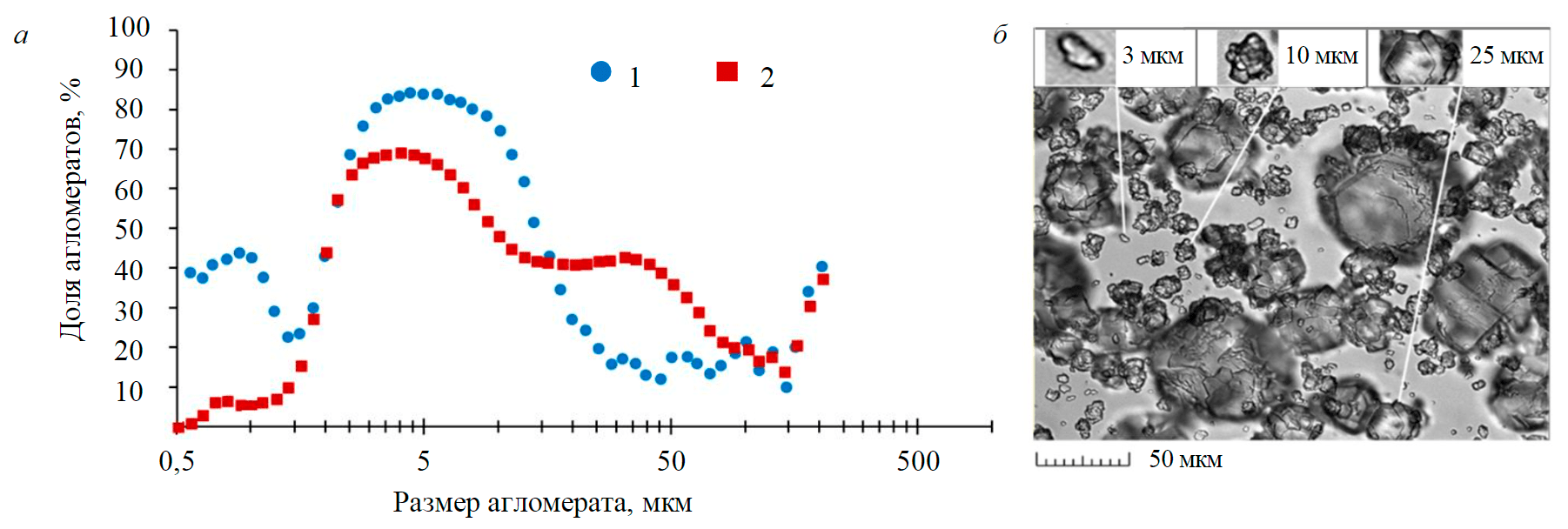
Рис.6. Доля агломератов в популяции кристаллов в зависимости от размера частиц: а – результаты расчета; whereб – микрофотография Содержание фракции –45 мкм: 1 – минимальное; 2 – максимальное
После неудачного результата моделирования, пришедшегося на январь 2015 г., новая модель самостоятельно выправилась, продемонстрировав наличие следующего максимума по содержанию фракции –45 мкм в феврале и минимума в апреле 2015 г.
Наиболее точное совпадение результатов расчетов с наблюдениями достигнуто для отношения A/C в маточном растворе (рис.5, в). Сильный шум на этом графике объясняется колебаниями состава и расхода алюминатного раствора, поступлением затравки с других участков, а наблюдаемая волна связана с изменением удельной поверхности собственной затравки.
Согласно результатам моделирования, больше всего агломератов содержится в диапазоне размеров 0,5-1,0 и 4-16 мкм (рис.6, а). Наличие первого пика совпадает с представлениями о том, что частицы размером 0-2 мкм демонстрируют ускоренный рост по сравнению с остальной популяцией [7]. Постоянное присутствие второго пика зафиксировано с помощью микроскопии, которая подтвердила, что частицы размером около 10 мкм отличаются ярко выраженной фрактальностью (рис.6, б).
Согласно результатам моделирования, доля агломератов в классах частиц непостоянна и подвержена таким же колебаниям, как и другие свойства популяции частиц. В периоды укрупнения затравки агломераты также укрупняются, что приводит к исчезновению первого пика в их содержании. В периоды измельчения затравки доля агломератов в мелких классах частиц увеличивается (рис.6, а).
Улучшенная модель в результате с проведенной настройкой обладает хорошей прогнозирующей способностью для содержания крупных классов частиц – коэффициент корреляции находится в диапазоне 0,78-0,85, среднеквадратичное отклонение, например для класса –45 мкм, составляет 6 %. По мере уменьшения размера частиц точность предсказания снижается. Для управления процессом декомпозиции критически важно, что с использованием новой модели достигнута приемлемая точность предсказания координат очередной точки перегиба у кривой изменения содержания класса –45 мкм (см. таблицу).
Выводы
- На основании проведенного исследования можно заключить, что процесс рождения с распространением является одной из форм развития популяции частиц в ходе разложения алюминатного раствора при низкой температуре. Он управляется активностью затравки, набирая скорость одновременно с агломерацией и замедляясь по мере снижения доли агломератов в популяции. Рождение с распространением является блокирующим процессом, препятствующим выходу вторичных зародышей в раствор.
- Конкуренция процессов вторичного зародышеобразования, агломерации и разрушения частиц придает им свойства колебательной системы. Эти колебания устойчивы и при определенных условиях могут стать незатухающими.
- Для определения реперных точек и фазы колебаний, скорости возбуждающих их процессов можно ввести новое свойство популяции – долю частиц в классах, представленную агломератами.
- Отсутствие в уравнениях (6) и (9), которые выражают интенсивность образования зародышей и разрушения частиц, параметров, характеризующих качество затравочной поверхности, ограничивает их применимость циклами кристаллизации, в которых предусмотрена агломерация мелкой затравки при высоких температурах. Контролируемая агломерация дает возможность снабжать второй этап декомпозиции активной затравкой и регулировать численность популяции агломератов. При этом существенно уменьшается амплитуда и период колебаний фракционного состава и продуктивности раствора. В циклах одноэтапной декомпозиции при низких температурах поддерживать постоянную активность поверхности затравки не удается, и это необходимо учитывать при математическом моделировании.
- Представленные обновленные модели процессов зародышеобразования, рождения с распространением и разрушения не могут в полной мере объяснить все изменения фракционного состава, наблюдаемые в процессе декомпозиции, как и имеющаяся архивная информация о процессе не раскрывает всей изменчивости его внешних условий. Тем не менее, представленные результаты расчетов продемонстрировали, что модель весьма корректно воспроизводит фазу, амплитуду и период основной моды колебаний.
Литература
- Golubev B.О., Chistyakov D.G. Patent N 2019661712 RF. PrecipExpert computer program. Publ. 05.09.2019 (in Russian).
- Altun O., Benzer H. Selection and mathematical modelling of high efficiency air classifiers. Powder technology. 2014. Vol. 264, p. 1-8. DOI: 10.1016/j.powtec.2014.05.013
- Balakin B.S., Hoffmann A.C., Kosinski P. Population Balance Model for Nucleation, Growth, Aggregation, and Breakage of Hydrate Particles in Turbulent Flow. American Institute of chemical Engineering Journal. 2010. Vol. 56. Iss. 8, p. 2052-2062. DOI: 10.1002/aic.12122
- Bekker A.V., Livk I. An Implicit FEM Solution of a PBE Model of Gibbsite Crystallization with Constant and Nonlinear Kinetics. Industrial & Engineering Chemistry Research. 2011. Vol. 50. Iss. 8, p. 4641-4652. DOI: 10.1021/ie1019326
- Bekker A.V., Li T.S., Livk I. Dynamic response of a plant-scale gibbsite precipitation circuit. Hydrometallurgy. 2016. Vol. 170, p. 24-33. DOI: 10.1016/j.hydromet.2016.06.002
- Bekker A.V., Li T.S., Livk I. Understanding oscillatory behaviour of gibbsite precipitation circuits. Chemical engineering research and design. 2015. Vol. 101, p. 113-124. DOI: 10.1016/j.cherd.2015.07.006
- Dirksen J.A., Ring T.A. Fundamentals of crystallization kinetic effects on particle size distributions and morphology. Chemical Engineering Science. 1991. Vol. 46. Iss. 10, p. 2389-2427. DOI: 10.1016/0009-2509(91)80035-W
- Elwell D., Schell H.J. Crystall Growth from High-temperature Solutions. London: Academic Press, 1975, p. 634. DOI: 10.1107/S0021889876012612
- Farhadi F., Babaheidary M.B. Mechanism and estimation of Al(OH)3 crystal growth. Journal of Crystal Growth. 2002. Vol. 234. Iss. 4, p. 721-730. DOI: 10.1016/S0022-0248(01)01763-8
- Hounslow M.J. A Discretized Population Balance for Continuous Systems at Steady State. American Institute of chemical Engineering Journal. 1990. Vol. 36. Iss. 1, p. 106-116. DOI: 10.1002/aic.690360113
- Anashkin V.S., Teslia V.G., Kuznetcov I.A. et al. Influence of impurities on grain size distribution and morphology of aluminium hydroxide at the precipitation technology. 15th international symposium of ICSOBA “Aluminium Industry within World Economy: Problems and Trends of Development”, 15-18 June 2004, St. Petersburg, Russia. ICSOBA, 2004, p. 148-154.
- Ilievski D., Livk I. An agglomeration efficiency model for gibbsite precipitationin a turbulently stirred vessel. Chemical Engeneering Science. 2006. Vol. 61. Iss. 6, p. 2010-2022. DOI: 10.1016/j.ces.2005.10.051
- Li T.S., Rohl A.L., Ilievski D. Modelling non-stationary precipitation systems: sources of error and their propagation. Chemical Engineering Science. 2000. Vol. 55. Iss. 24, p. 6037-6047. DOI: 10.1016/S0009-2509(00)00210-4
- Litster J.D., Smit D.J., Hounslow M.J. Adjustable Discretized Population Balance for Growth and Aggregation. American Institute of chemical Engineering Journal. 1995. Vol. 41. Iss. 3, p. 591-603. DOI: 10.1002/aic.690410317
- Livk I., Ilievski D. A macroscopic agglomeration kernel model for gibbsite precipitation in turbulent and laminar flows. Chemical Engineering Science. 2007. Vol. 62. Iss. 14, p. 3787-3797. DOI: 10.1016/j.ces.2007.03.030
- Livk I., Pohar C., Ilievski D. Estimation of Batch Precipitation Kinetics by a Simplified Differential Method. American Institute of chemical Engineering Journal. 1999. Vol. 45. Iss. 7, p. 1593. DOI: 10.1002/aic.690450721
- Lotka A.J. Elements of Physical Biology. Baltimore: Williams and Wilkins Co., 1925, p. 495.
- Lynch A.J. Mineral Crushing and Grinding Circuits: Their Simulation, Optimisation, Design and Control. Amsterdam: Elsevier Scientific Publishing Company. 1977, p. 342.
- Misra C. The Precipitation of Bayer Aluminium Trihydroxide: PhD Thesis. University of Queensland. Brisbane, Queensland, Australia, 1970, p. 236.
- Nageswararao K., Wiseman D.M., Napier-Munn T.J. Two empirical hydrocyclone models revisited. Mineral Engineering. 2014. Vol. 17. Iss. 5, p. 671-687. DOI: 10.1016/j.mineng.2004.01.017
- Ramkrishna D. Population balances. Theory and Applications to Particulate Systems in Engineering. London: Academic Press, 2000, p. 355. URL:https://www.sciencedirect.com/book/9780125769709/population-balances#book-info (date of access 01.12.2020).
- Simulating Comminution and Classification Circuits with JKSimMet. 6 June 2020. URL:http://jktech.com.au/jksimmet (date of access 01.12.2020).
- Spicer P.T., Pratsinis S.E. Coagulation and fragmentation: universal steady-stateparticle-sizedistribution. American Institute of chemical Engineering Journal. 1996. Vol. 42. Iss. 6, p. 1612-1620. DOI: 10.1002/aic.690420612
- Stephenson R. Equivalence of Growth Rate and Yield Methods. Proceedings of 35th International ICSOBA Conference, 2-5 October 2017, Hamburg, Germany. ICSOBA, 2017. Vol. 46, p. 313-318.
- SysCAD – Innovative Software for Plant Simulation. 6 June 2020. URL: https://help.syscad.net/index.php/Precipitation3 (date of access 01.12.2020).
- Tachamper O. Improvements by the new Alusuisse process for producing coarse aluminium hydrate in the Bayer process // Light metals.Warrendale, Pennsylvania. TMS (The Minerals, Metals & Materials Society). Springer, 2016, p. 534-540. DOI: 10.1007/978-3-319-48176-0_74
- White E.T., Bateman S.H. Effect of caustic concentration on the growth rate of Al(OH)3 particles. Light Metals. Warrendale, Pennsylvania. TMS (The Minerals, Metals & Materials Society). Springer, 1988, p. 157-162.
- Yin J., Chen Q., Yin Zh., Zhang J. Study on the oscillation phenomena of particle size distribution during the seeded agglomeration of the sodium aluminate liquors. Aluminum Committee at the 135th TMS annual meeting, 12-16 March, 2006, San Antonio, Texas, USA. P. 173-176. URL: https://www.tib.eu/en/search/id/TIBKAT%3A526000430/Light-metals-2006-proceedings-of-the-technical/ (date of access 01.12.2020).
