Development of viscoelastic systems and technologies for isolating water-bearing horizons with abnormal formation pressures during oil and gas wells drilling
- 1 — Dr.Habil. professor Saint Petersburg Mining University ▪ Orcid ▪ Elibrary ▪ Scopus ▪ ResearcherID
- 2 — postgraduate student Saint Petersburg Mining University ▪ Orcid
- 3 — Dr.Habil. Rector Grozny State Oil Technical University named after academician M.D. Millionshchikov ▪ Orcid
Abstract
Article provides a brief overview of the complications arising during the construction of oil and gas wells in conditions of abnormally high and abnormally low formation pressures. Technological properties of the solutions used to eliminate emergency situations when drilling wells in the intervals of catastrophic absorption and influx of formation fluid have been investigated. A technology for isolating water influx in intervals of excess formation pressure has been developed. The technology is based on the use of a special device that provides control of the hydrodynamic pressure in the annular space of the well. An experiment was carried out to determine the injection time of a viscoelastic system depending on its rheology, rock properties and technological parameters of the isolation process. A mathematical model based on the use of a special device is presented. The model allows determining the penetration depth of a viscoelastic system to block water-bearing horizons to prevent interformation crossflows and water breakthrough into production wells.
Introduction. Drilling of oil and gas wells is accompanied by high risks associated with complications, such as sticking of the drilling string and casing in the borehole, cavings and collapses of unstable rocks, absorption of drilling process fluids and fluid influx [1, 12]. Analysis of the investigations' results for emergency situations showed that more than 30 % are losses of drilling and cementing fluids, as well as gas, oil and water influx (GOWI) at various stages of well construction [5-7].
Most of the gas and gas condensate fields are at a late stage of development and are characterized by low formation pressures, among them – Alberta, Denver, Dneprovsko-Donetsky, Predappalachsky, San Huan, Severo-Predkarpatsky, Sunliao, Shivu and other oil and gas basins of the world. Such oil and gas provinces in the Russian Federation as Timan-Pechora, Leno-Tunguska, West Siberian, Volga-Ural can also be named [10, 24]. Further development of fields is ensured by drilling additional production and injection wells and is carried out using technologies aimed at reducing the risks of fluid sorptions [21, 23].
Oil and gas fields, characterized by increased and abnormally high formation pressures, are quite widespread. Among them are the deposits in Europe (Adriatic-Ionian, Aquitaine, Vienna-Moravian, Rhein, Pannonian oil and gas basins, etc., most of the shelf of the North Sea), North America (shelf of the western and eastern coasts, Mackenzie delta region ), most of the US states (the Gulf of Mexico region), South America (the shelf of the west coast of Colombia, Peru, Ecuador, the shelf of the east coast of Brazil, Venezuela, Guyana), Africa (Algeria, Morocco, Nigeria, the Nile delta region, the Algerian-Libyan oil and gas basin), in western and northern Australia, Papua New Guinea, on the territory of the Indonesian archipelago, on the island of Taiwan, in Japan (on the island of Honshu), in the fields of the South China Sea, the Persian Gulf, almost all oil and gas basins and provinces of the Russian Federation [2, 17, 25].
The construction and operation of wells in such conditions may be accompanied by an increased likelihood of formation fluid influx. They can lead to both open blowing during drilling and interformation crossflows during operation. High-pressure formations in addition to oil and gas can contain brines, both weak and highly concentrated. Their presence may cause problems associated with the coagulation of the drilling mud, fallout of salts into the wellbore and a decrease in its crossflow section, sticking and breakage of the drilling tool [1]. One of the problems for abnormally high formation pressures (AHFP) is a decrease in the ratio of absorption and hydraulic fracturing pressures to the formation pressure compared to the conditions of normal and abnormally low formation pressures (ALFP). This leads to a decrease in the “working window”, within which the equivalent circulation density of the solution can vary, and to an increase in the likelihood of drilling technological and cementing fluid absorption [3, 19, 30].
High quality sealing of oil and gas wells and reduction of interformation crossflows remains the most important condition for their effective use as long-term structures [8, 28]. Sealing devices used in this case should allow for accident-free carrying out of various works in the well and ensure the fulfillment of technical, environmental and economic requirements [4].
There are many methods and techniques for blocking water-producing formations during repair and isolation works and express repairs to restore the structural integrity of fluid producing wells [13 - 15, 18]. The technologies used to isolate formations with abnormal pressures during well drilling are not effective, since they require additional tripping operations [26]. In this regard, the development of technology, technical tools and compositions of process fluids for isolation of formations with abnormal pressures without stopping the drilling process is relevant [32]. Scientific and technical research and development in this area will reduce the timing of drilling operations in the well and ensure its long-term and accident-free operation.
Methodology and discussion. To carry out the drilling process in the conditions of abnormally low pressure and abnormally high pressure, lightweight drilling fluids are used, including foam systems and gel-forming compounds (VES) [29]. Preparation of three-phase foams and gel-forming compositions was carried out according to the method described by N.I.Slyusarev [11]. Study of the kinetics of foam destruction was carried out within 30 minutes from the moment of its preparation.
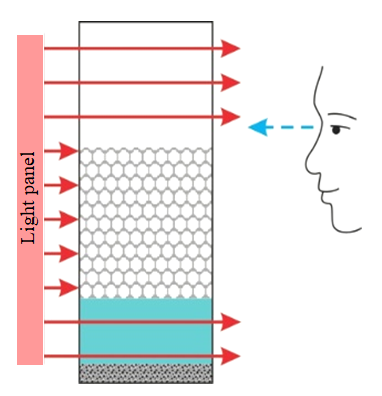
Measuring of foams was carried out according to the method of the Max Planсk Institute for Colloids and Surfaces [16], Principle of the method is the determination of the change in the height of the liquid and foam column and is as follows: a glass with three-phase foam was located between the light source and the observer (Fig.1), through equal time intervals (every 300 s) a change in the height of the liquid and foam column was observed.
The research methodology for three-phase foam and gel-forming composition is similar, since both fluids are non-Newtonian and can change their volume depending on the conditions and nature of use. Developed composition of the three-phase foam decreases in volume at high pressure and temperature, while effectively blocking formations with abnormally low formation pressure and high temperature, but does not solve the problem of blocking formations with water influxes at AHFP.
Density and rheological properties of the developed compositions were studied according to GOST 33213-2014 on standard laboratory equipment: OFITE HPHT viscometer (model 1100), OFITE HPHT Dynamic filter press, 35SA viscometer (FANN), lever scales in a FANN 140 case [20, 27]. All experimental investigations were carried out in the laboratory of drilling fluids at the Department of Well Drilling in Saint Petersburg Mining University.
Nine compositions were selected as the investigated blocking three-phase foams for ALFP. Concentration of surfactants, stabilizing and structure-forming components were varied. Table 1 shows the component compositions of the investigated solutions.
Table 1
Composition of the investigated solutions
| Reagents | Solutions, % | ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| Biopolymer | 2,6 | 1,5 | 1,5 | 0,5 | 0,3 | 0,3 | 0,4 | 0,3 | 0,3 |
| Surfactant | 0,1 | 0,1 | 0,1 | 0,1 | 0,06 | 0,1 | 0,1 | 0,08 | 0,04 |
| Weighting agent | 2,0 | 2,0 | 2,0 | 1,0 | 3,0 | 2,0 | 2,0 | 2,0 | 3,5 |
| pH regulator | 0,06 | 0,06 | 0,06 | 0,06 | 0,06 | 0,06 | 0,06 | 0,06 | 0,06 |
| Bactericide | 0,05 | 0,05 | 0,05 | 0,05 | 0,05 | 0,05 | 0,05 | 0,05 | 0,05 |
During the research, it was not possible to determine the conditional viscosity of the compositions 1-4, therefore, further work on them was not carried out. Compositions of the solutions are stable, but not flowing. High relative viscosity of these kill fluids can affect the pump performance.
Dynamic viscosity measurements were carried out at different shear rates for compositions 5-9. Indicators of dynamic viscosity are close enough for all compositions, however, the stability turned out to be acceptable only for compositions 7 and 9 (no more than 20 kg/m3), compositions 5, 6 and 8 separated and showed rather low stability values, which is unacceptable.
Table 2 shows the results of the research for determining the ultimate dynamic shear stress of blocking three-phase foams under standard conditions and reservoir temperature of 900 [31].
Table 2
Results of determining the ultimate dynamic shear stress of blocking three-phase foams
| Properties | Solutions | ||||
| 5 | 6 | 7 | 8 | 9 | |
| Plastic viscosity, mPa•s | 12 | 12 | 6 | 11 | 4 |
| Dynamic shear stress, Pa | 18,24 | 18,24 | 19,2 | 12,48 | 22,08 |
Compositions 7 and 9 are considered for filtration assessment, since the study of other compositions was impractical due to the relatively high values of plastic viscosity. To ensure blocking of a permeable formation, the compositions must have nonzero filtration, however, increased values (more than 10 cm3/30 min) can lead to global penetration into the horizon and increased consumption of blocking solutions. Therefore, the obtained filtration values of the solutions (Table 3) are satisfactory and can be recommended for use at ALFP.
Table 3
Filtration results for solutions 7 and 9
| Properties | Solutions | ||
| 7 | 9 | ||
| Test temperature, 0С | 20 | 20 | 90 |
| Filtration, cm3/30 min | 8,8 | 8 | 8 |
| Filter cake thickness, mm | 1,6 | 1,6 | 1,8 |
Table 3 shows that the filtration of the two selected solutions of three-phase foams satisfies the requirements for the blocking composition at ALFP, and solution 9 is stable when the test temperature changes.
Investigations of the gel-forming composition included the determination of the solution filtration, physical, mechanical and rheological parameters. Table 4 presents the results of these investigations for VES of various concentrations.
Table 4
Table 4 Physical, mechanical and rheological properties of liquids based on polymer composition «SPMI-7»
| Investigated properties | Solution base | ||||
| Technical water at CSPMI-7 = 0,625 % | Technical water at CSPMI-7 = 1,25 % | Technical water at CSPMI-7 = 2,5 % | Technical water at CSPMI-7 = 5,0 % | Drilling mud at CSPMI-7 = 1,25 % | |
| Demsity \(\ \rho\), kg/m3 | 1,0 | 1,0 | 0,95 | 0,97 | 1,02 |
| Conditional viscosity Т, с | 25 | 250 | None | None | None |
| Static filtration Ф, cm3/30 min | >500 | >500 | Possible water loss (~8 ml) | Possible water loss | Possible water loss |
| Static shear stress after 10 s and 10 min of rest, SSS1/10, dPa | 2/2 | 5/5 | 33/30 | 114/100 | 39/48 |
| Dynamic shear stress \(\ \tau_{0}\), Pa | 0 | 0 | 20,87 | 356,44 | 91,5 |
| Plastic viscosity \(\ \eta_{пл}\), mPa s | 31,74 | 79 | 113 | 39,7 | 58,16 |
| Time for formation of an immobile structure (structuring time), min | – | – | Instant | Instant | – |
| Flowability, sm | >25 | >25 | None | None | 11,25 |
| Plastic durability Pт, Pa | 0 | 0 | 0 | 0 | 0 |
| pH | – | – | – | – | – |
When 2.5-5 % “SPMI-7” polymer is added to distilled water, the mixture is crosslinked and there is no filtration. In mineralized water, the “SPMI-7” polymer does not turn into a gel and filters well. For pumping the solution, the maximum permissible concentration of the polymer “SPMI-7” in solutions is 1.25 %. The beginning of the polymer crosslinking process begins at a concentration of 0.625, which will allow blocking the water producing horizons.
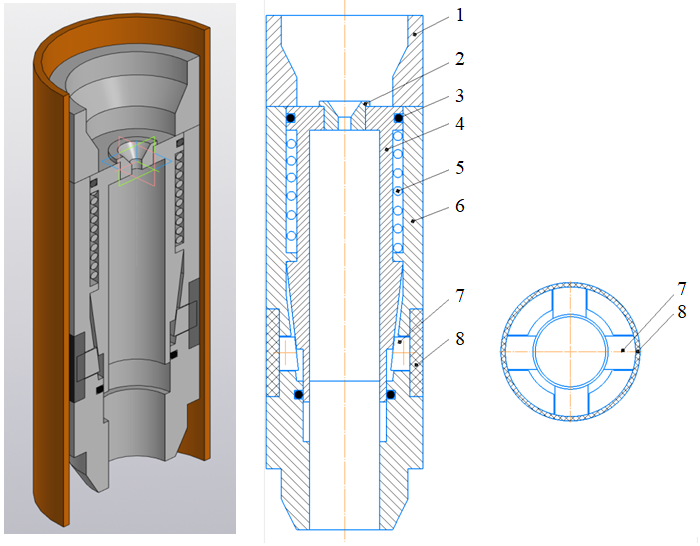
Technical equipment. To implement the technology of the formation isolation without stopping of drilling, it is proposed to use the developed VES composition – process fluid with the addition of the “SPMI-7” polymer solution and a borehole hydraulic packer [9].
The operation principle of a hydraulic packer is based on decreasing (increasing) the annular gap by creating pressure in the annulus.
The device works as follows. Under the effect of the hydraulic pressure of the solution through the sub 1 on the nozzle 2, the piston 4 moves with the sliding of the sealing ring 3 along frame 6 with the simultaneous compression of spring 5, leading to the movement of plates 7 and the expansion of cuff 8 until the stop of piston 4 at the lowest point of frame 6 (Fig.2).
Developed VES composition together with a pressure-regulating device allows isolating formations with abnormally high pressure without stopping the drilling process, as well as carrying out repair and isolation work in the operating wells.
Modeling the isolation process of water-producing formations. For verification of experimental investigations to determine the isolation of water-producing horizons, mathematical modeling (computational experiment) was carried out. It allows application of Darcy's law together with the equations of continuity, pore fluid state and volumetric force [31].
Geometric conditions of the surface must be taken into account in the mathematical model of the injection process for any fluid. They include characteristics of the porous medium, properties of the fluids and physical laws of the fluid behavior in the porous medium. Mixture model is a macroscopic two-phase flow model, in many ways similar to the bubble flow model. It tracks the average phase concentration, or volume fraction, and solves a single pulse equation for the mixture velocity. The model is suitable for mixtures of solid particles or liquid droplets immersed in liquid.
It is convenient to write the geometric conditions of the surface by setting the equations for the connection of classical Cartesian coordinates with polar coordinates, where the pole is the center of the circular sector formed by the half of the pipe under consideration (in the X-Y section), because then everything will be reduced to specifying the radius.
Simulation of fluid flow in free and porous media uses the Navier – Stokes equation to describe the flow in open areas and the Brinkman equation to describe the flow in porous media:
where \(\ \rho\) – fluid density, kg/m3; \(\ \epsilon_{p}\) – formation matrix porosity (dimensionless number between 0 and 1); Qm – volume of fluid passing through the reservoir, kg/(m3∙s).
Darcy's Law states that the velocity field is determined by the pressure gradient, fluid viscosity and porous medium permeability:
where u – Darcy velocity vector, m/s; k – porous medium permeability, m2; μ – fluid dynamic viscosity, Pa∙s; \(\ \nabla \) – nabla operator – symbolic vector replacing gradient symbol; р – fluid pressure, Pa.
Permeability k is the resistance to flow over a representative volume of solid grains and pores. The fields u and p are determined both in free flow regions and in porous regions. This means that the pore pressure is continuous at the interface between the free flow region and the porous region. Continuity is ensured between the fluid velocity in free flow and the Darcy velocity in the porous region. The continuity of u and p implies a break in stresses at the interface between the free-flow region and the porous region. The difference corresponds to the stress absorbed by the rigid porous matrix, which is an implicit consequence in the formulations of the Navier – Stokes and Brinkman equations.
Applying the theory of single-phase flow, the interface between fluid flows based on the Navier – Stokes equations, we use the formula
Linear material of volumetric force is specified by the force F in the right side of the Navier-Stokes or Brinkman equations, depending on whether the node of porous matrix properties is active for the fluid. Then it is used to include gravity effects in the model. Theory of boundary conditions for the walls of the medium should be noted there. Sliding condition assumes that there are no viscous effects on the sliding wall and, therefore, the boundary layer does not develop. From a modeling point of view, this is a reasonable approximation if the important effect of the wall is to prevent the fluid from leaving the area. Boundary condition is a combination of the Neumann condition. Mathematically, this restriction can be formulated as follows:
where n – normal vector; K – Lagrange multipliers.
Term “no penetration” has the priority over Neumann part of the condition, and therefore the expression is equivalent to
and shows that there is no flow through the boundary and no viscous stress in the tangential direction.
For a moving wall with translational velocity utr, u in equations (4) - (5) is replaced by the relative velocity urel = utr – u.
For a turbulent flow, the turbulence variables generally obey the homogeneous Neumann conditions. For example, \(\ \nabla kn=0 \),
Equation (6) describes Darcy's law in a porous medium and models the flow of fluid through intervals in a porous medium. Equations (5), (6) can be used to simulate low-velocity flows or media where the permeability and porosity are very small and the pressure gradient is the main driving force, and the flow mainly depends on the frictional resistance inside the pores. Darcy's Law can be used for stationary and time-dependent analyzes.
If considering a linear material of fluid medium in the modeling programming, fluid and matrix properties, boundary conditions (no flow), and initial fluid values are added.
For a porous medium, the global transfer of pulse by shear stresses in a liquid is often insignificant. Pore walls impede the transfer of pulse between the liquid occupying different pores. General alternative approach is to homogenize porous and fluid media into a single medium.
Laws (5), (6) are the equations of continuity for laminar flow. Porous reservoir model is also described by the continuity equation.
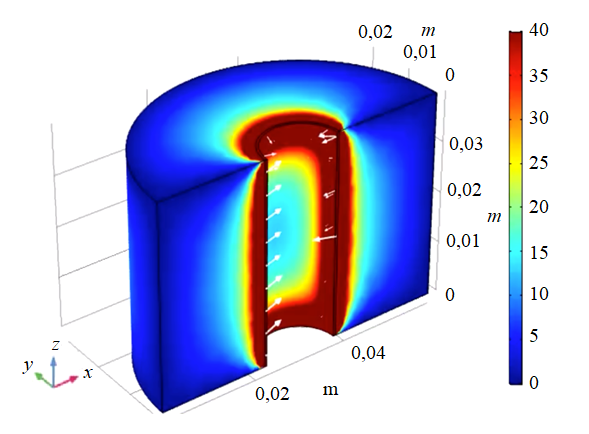
Visualization of the VES injection process is carried out using the COMSOL Multiphysics® (Fig.3-5). Equations of connection for classical Cartesian coordinates with polar coordinates are used, where the pole is the center of the circle sector formed by the considered half of the pipe.
Liquid material was selected to be used to input fluid properties and movement characteristics to model fluid flow through intervals in a porous medium. Interface is used to simulate low-velocity flows or media where the permeability and porosity are very small and the pressure gradient is the main driving force, and the flow mainly depends on the frictional resistance inside the pores.
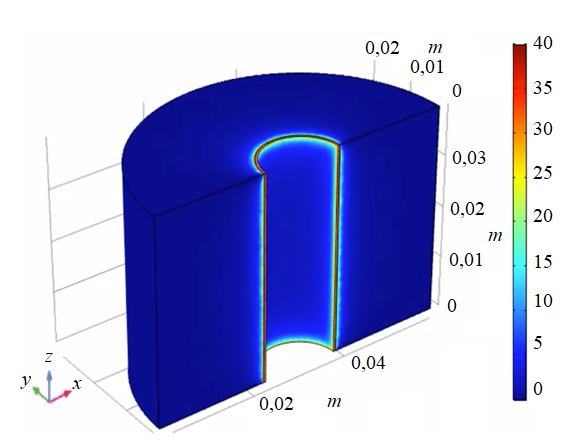
Figure 3 shows the visualization of the formation fluid flow into the well during drilling of water-producing horizons.
It is necessary to isolate water-producing horizons during drilling-in. Injection of the developed isolating fluid (VES) using a hydromechanical packer will limit water influx into the well. (fig.2).
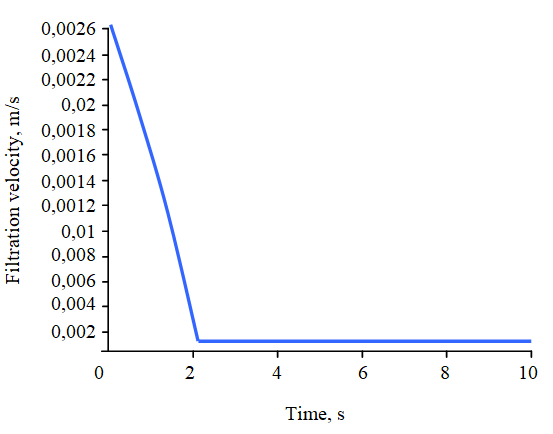
Graph in fig.5 does not go to zero, since the formation is temporarily blocked by a non-solidifying VES. In 2 seconds after the VES injection, the blocking of the penetrating horizons occurs.
Conclusion. As a result of drilling wells in oil and gas areas, a reliable, durable isolated channel that connects the productive horizon to the day surface must be created.
Developed foams for creating a blocking screen in ALFP are stable and are not destructed with deepening of the borehole bottom, which is confirmed by the presented laboratory investigations. Ground calcium carbonate gives stability to the three-phase foam.
Developed VES composition together with the proposed device – a pressure regulator will allow isolating formations with ALFP without stopping the drilling process, as well as carrying out repair and isolation work in the operating well stock. According to the research results of pumping the solution, the maximum permissible concentration of the “SPMI-7” polymer in solutions is 1.25 %. Beginning of the polymer crosslinking process starts at a concentration of 0.625 %, which will block the water-producing horizons. Application of isolation technology using the proposed equipment at a constant drilling speed, with a change in the effective viscosity and simultaneous adjustment of the gap in the annular space will ensure the isolation of a water-saturated reservoir.
Darcy's Law, together with the equations of continuity and state for a pore fluid, provides a complete mathematical model suitable for a variety of applications connected with pore flows where pressure gradient is the main driving force.