Метод оптимизации, основанный на концепции удельной механической энергии, для повышения производительности бурения: пример практического применения
- 1 — научный сотрудник Технологический университет Саханд ▪ Orcid
- 2 — канд. техн. наук доцент Технологический университет Саханд ▪ Orcid
Аннотация
В течение многих лет в буровой промышленности предпринимались попытки повысить производительность бурения и снизить затраты. Производительность бурения можно оценить, сравнив приложенную энергию, т.е. удельную механическую энергию, с прочностью горной породы. Удельная механическая энергия определяется как энергия, необходимая для разрушения единицы объема горной породы. С годами эта концепция совершенствовалась, и исследователи предлагали различные модели. Удельная механическая энергия напрямую влияет на производительность бурения, поскольку избыточная энергия может привести к вибрации бурильной колонны и износу долота. В исследовании создана база данных путем сбора информации о бурении и материалах каротажа свиты Асмари на одном из нефтяных месторождений Ирана. Рассмотрены различные формы удельной энергии для разработки соответствующей модели на основе условий эксплуатации и буримого пласта. Кроме того, рассчитана ограниченная прочность породы на сжатие в изучаемой скважине. Исследования показали, что разработанная модель удельной энергии выдает реалистичные значения энергии, поскольку включает все соответствующие параметры, с результативным значением, близким к прочности горной породы. На основе сравнения удельной механической энергии с ограниченной прочностью на сжатие были определены оптимальные буровые параметры: диапазон нагрузки на долото от 22,24 до 44,48 кН, диапазон расхода бурового раствора от 0,027 до 0,029 м3/с, диапазон крутящего момента от 2522 до 3091 Н·м и диапазон скорости вращения от 160 до 180 об/мин. Также в исследуемой скважине была обнаружена зона неэффективного бурения, где приложенная энергия, избыточная по сравнению с прочностью породы, привела к повреждению бурового долота и значительному снижению скорости проходки. Результаты подчеркнули важность оценки производительности бурения в процессе работы, когда экономически и технически осуществимое решение можно принять путем сравнения поверхностной энергии на входе с прочностью породы.
Введение
Целью оптимизации бурения является достижение баланса между приложенной поверхностной энергией и энергией, требуемой для разрушения горных пород, поскольку часть приложенной энергии с поверхности обычно теряется из-за вибраций и колебаний в бурильной колонне и не вносит вклад в процесс разрушения горных пород. Поэтому были проведены различные исследования и эксперименты для минимизации нежелательных форм приложенной энергии и установления баланса между приложенной и требуемой энергиями [1, 2].
Впервые анализ применяемой в процессе бурения поверхностной энергии провел Р.Тил в 1965 г. В исследовании была введена механическая удельная энергия (МУЭ) как энергия, необходимая для разрушения и бурения единицы объема породы. Эта первоначальная модель включала два компонента – осевую силу, связанную с нагрузкой бурильной колонны на долото, и крутящий момент, создаваемый вращением бурильной колонны [3]. В последующих исследованиях первоначальная модель была оптимизирована и изменена с учетом различных эксплуатационных и геологических условий в процессе бурения [4]. В современных работах, посвященных МУЭ, в первоначальную модель Р.Тила включают влияние различных параметров, таких как механические свойства породы, эксплуатационные параметры и характеристики бурового раствора [5-7].
В 1960-2000 гг. в ранних моделях МУЭ, таких как модели Тила и Рабии, учитывались только влияние поверхностных параметров и факторы, связанные с буровой установкой. В этот период, как правило, не принималось во внимание влияние гидравлических параметров бурового раствора и характеристик пласта. Эти модели были в первую очередь направлены на упрощение анализа движения бурильной колонны и игнорировали износ долота или реологические свойства бурового раствора. Современные исследования показали значимость реологических свойств бурового раствора для производительности бурения [8, 9].
Все изменило влияние технологического прогресса и усложнение буровых работ после 2000-х гг. [5, 10, 11]. В начале 2000-х гг. исследователи пытались улучшить модели МУЭ и изучить влияние дополнительных факторов. Например, модели, предложенные Дюпри и Кедерицем, применяли концепции механической производительности и предела прочности породы на сжатие (ППС), что является значительным достижением в развитии моделей МУЭ. Однако последующие исследования показали, что ППС породы не может полностью отражать влияние ее свойств на удельную энергию. На величину МУЭ влияют и другие параметры, такие как литологический состав, прочность на сдвиг, твердость и пористость [5, 12, 13].
С конца 2000-х гг. исследователи сосредоточились на интеграции в модели МУЭ гидравлических буровых параметров. Например, гидравлические параметры считались значимым фактором в моделях, предложенных М.Арментой и К.Моханом. Интеграция гидравлических параметров позволила получить более подробную информацию о характеристиках бурового раствора и их влиянии на МУЭ. Это не только повысило точность моделей, но и улучшило их прогностическую способность и адаптивность к различным буровым условиям [14-16]. В более современных моделях [17-19] учитывалось влияние почти всех поверхностных параметров, связанных с гидравликой буровой установки и бурового раствора. Кроме того, эти модели учитывали влияние наклона скважины и, в случае применения забойных двигателей, влияние параметров двигателя. Забойные двигатели показали оптимальную производительность бурения в вертикальных и наклонно-направленных скважинах [20, 21].
Если МУЭ чрезмерно высока, это может привести к вибрации бурильной колонны, разрушению долота, снижению скорости проходки и в конечном итоге к износу и усталости оборудования [22]. Согласно предыдущим исследованиям, минимальная прилагаемая МУЭ должна быть равна ППС породы [3, 23, 24]. В некоторых исследованиях оптимизации бурения использовалась концепция МУЭ. Ф.Е.Дюпри и др. [11] обнаружили, что если отношение МУЭ к объему породы остается постоянным или относительно постоянным, буровое долото работает с максимальной производительностью. Авторы также продемонстрировали, что если МУЭ остается стабильной при увеличении нагрузки на долото, производительность долота эффективна. Однако если МУЭ непостоянна и увеличивается, это указывает на то, что долото неэффективно и бурение отклонилось от эффективной зоны.
М.Армента [12] продемонстрировал, что бурение неэффективно, когда удельная энергия увеличивается, а скорость проходки уменьшается. Согласно его выводам, удельная энергия увеличивается, когда нагрузка на долото превышает определенный порог. Он также определил границу между эффективными и неэффективными буровыми работами.
Н.Рафатян и др. [13] экспериментально исследовали изменение МУЭ во время бурения долотами с синтетическими алмазами. Результаты показали, что даже небольшой рост ограничивающего давления значительно увеличивает энергию, необходимую для разрушения как проницаемых, так и непроницаемых пород, что потенциально снижает производительность бурения. Исследование показало, что рост МУЭ гораздо более выражен в диапазоне ограничивающего давления 0-1,034 МПа по сравнению с диапазоном 1,034-6,55 МПа.
И.Д.Томсон и Р.Матур [14] улучшили производительность в проекте глубоководного бурения, отслеживая и анализируя данные МУЭ поверхности и скважины и объединяя их с параметрами бурения с применением забойного двигателя. Поскольку бурильная колонна часто испытывает вибрации, когда долото перемещается из мягкого пласта в пласт более сложного строения, для прогнозирования этих переходных зон авторы использовали буровые данные в реальном времени и мониторинг МУЭ. Таким образом буровая бригада могла быстро ввести данные для корректировки параметров и эффективного бурения.
С.Хаммоутен [15] оптимизировал буровые операции, сравнив МУЭ и прочность на одноосное сжатие (ПОС). Он вычислил, что коэффициент механической производительности для долот с синтетическими алмазами составляет от 0,26 до 0,64. Этот коэффициент производительности использовался для оптимизации конструкции долота и улучшения процесса разрушения горных пород, гарантируя, что такие факторы, как внезапные подземные изменения пласта, неоднородность пласта и вибрации, не будут угрожать производительности бурения.
Б.М.Мохаммади и др. [19] исследовали влияние геомеханических параметров на изменения удельной энергии на одном из нефтяных месторождений на юго-западе Ирана. Сначала они собрали геологические, каротажные, буровые, керновые и поровые данные из разных скважин для построения одномерной геомеханической модели. Затем с помощью многомерной регрессионной модели для установления связи между удельной энергией и влияющими на нее параметрами исследователи обнаружили, что такие параметры, как ПОС, угол внутреннего трения и скорость потока, входят в число наиболее значимых факторов, влияющих на удельную энергию.
С.Менанд и К.Миллс [25] обнаружили, что по МУЭ нельзя оценить эффективность бурения. Они представили новый метод, объединяющий МУЭ с показателем энергии бурения, чтобы лучше определить причины неэффективности бурения. Предметные исследования показали, что отношение МУЭ к энергии бурения может помочь обнаружить конкретные проблемы и неэффективное бурение, например скачкообразную подачу и износ долота.
В.Рамба и др. [26] провели исследование оптимизации буровых параметров и увеличения скорости проходки в разведочной скважине. Контролируя построенные графики МУЭ и скорости проходки, они определили зоны эффективного и неэффективного бурения. Аналогичным образом, изучая графики удельной энергии и скорости проходки, ученые рассчитали оптимальный требуемый расход бурового раствора. Внедрив оптимизированные буровые параметры, они добились снижения приложенной энергии на 75 %.
Фактором, влияющим на изменение значения МУЭ, является конструкция долота. К.Сюн и др. [16] исследовали влияние глубины, угла и скорости резания жала поликристаллического алмазного долота на изменения МУЭ. Результаты показали, что МУЭ значительно уменьшается с увеличением глубины резания, а скорость резания оказывает незначительное влияние на значе-ние МУЭ.
Как видно, в разных исследованиях для оптимизации бурения используются различные модели МУЭ с определенными изменениями, и универсальной модели МУЭ не существует. В данном исследовании собраны геологические, каротажные и буровые данные из скважины континентального месторождения, и различные модели МУЭ исследованы на основе фактических данных. Предложено измененное уравнение для изучаемого месторождения. Измененная модель МУЭ применялась для обнаружения зон неэффективного бурения, с этого времени можно вносить необходимые изменения в управляемые буровые параметры для оптимизации буровых операций.
Методы
Целью буровых работ является разрушение и фрагментация горных пород подземных пластов. В ходе этого процесса за счет приложения энергии с поверхности происходят преобразование единицы объема горной породы в более мелкие куски разного размера и разрушение горной породы. Поэтому простым определением МУЭ можно считать отношение подводимой энергии к единице объема разрушенной горной породы [3, 13]:
МУЭ можно определить как энергию, необходимую для бурения единицы объема породы [3]. Приложенная поверхностная энергия может включать осевые, гидравлические и крутящие компоненты. Принимая во внимание эти компоненты, определение МУЭ можно выразить более полно следующим образом [2, 18]:
Уравнение (1) применялось в измененном виде в различных моделях с введением разных эксплуатационных и геологических условий бурового процесса. Первая модель была представлена Р.Тилом (1965) как энергия, необходимая для разрушения, удаления и бурения единицы объема породы. Она состояла из двух частей – приложенной осевой и вращательной энергий и имела следующий вид [3]:
где et – приложенная осевая энергия; er – вращательная энергия.
Рассмотрев эти типы энергий, Р.Тил представил модель следующим образом:
где Плд – площадь долота; СВ – скорость вращения; КМ – крутящий момент; СП – скорость проходки; ННД – нагрузка на долото.
Пессье и Фир провели эксперименты на моделируемой буровой установке и рассмотрели крутящий момент на долоте в качестве основного входного параметра для расчета МУЭ. Исследователи отметили, что крутящий момент на поверхности, зарегистрированный во время бурения, не соответствует фактическому крутящему моменту на долоте. Поэтому они ввели коэффициент трения скольжения, характерный для долота, как функцию отношения крутящего момента на поверхности, приложенного к нагрузке на долото, и диаметра долота. Коэффициент трения скольжения может оценить крутящий момент на долоте, когда измерения крутящего момента под поверхностью недоступны [24]. Учитывая коэффициент трения скольжения, МУЭ можно рассчитать следующим образом:
где µд – коэффициент трения скольжения долота; дмд – диаметр долота, согласно исследованию М.Арменты [12], дмд = 0,25 для шарошечных долот, дмд = 0,5 для долот, армированных поликристаллическими алмазами.
Ф.Дюпри и др. [27] подчеркнули важность мониторинга МУЭ для оптимизации бурового процесса. На основе изучения производительности долота по полевым данным исследователи предположили максимальную производительность долота 40 % при среднем значении 35 % независимо от типа долота и внесли изменения в модель МУЭ. Результаты показали, что значения МУЭ из следующей формулы примерно равны ограниченной прочности породы на сжатие:
М.Армента [12], рассматривая влияние гидравлической энергии бурового раствора в модели МУЭ, ввел понятие удельной энергии бурения:
где λ – гидравлический коэффициент долота, зависящий от диаметра долота; ГМд – гидравлическая мощность долота.
Коэффициент гидравлической мощности долота можно определить по размеру долота, используемого во время бурения [12]. В средних и мягких породах гидравлическая энергия бурового раствора может ослабить пласт до того, как долото коснется его [18]. К.Мохан и др. [2, 18], рассматривая воздействие гидравлической силы бурового раствора, ввели понятие удельной гидромеханической энергии (УГМЭ) как силы действующей на долото, равной и противоположной воздействию жидкости на пласт:
где ННДэ – эффективная нагрузка на долото; ΔДд – перепад давления на долоте; η – коэффициент снижения энергии; Р – расход бурового раствора.
О.Олорунтоби и др. [7] раскритиковали модель УГМЭ и подчеркнули отсутствие нормального градиента порового давления и эквивалентной циркуляционной плотности бурового раствора (ПБР) в расчете МУЭ. В связи с этим они предложили расширить модель УГМЭ следующим образом:
где НГПД – нормальный градиент порового давления; ЭЦП – эквивалентная циркуляционная плотность бурового раствора; ПБР – плотность бурового раствора; СПП – суммарная площадь потока сопел; МЛП – межлопастная площадь как пространство, где скапливается буровой шлам.
Основное применение концепции МУЭ – оптимизация энергии бурения с точки зрения приложенной поверхностной энергии [4]. Производительность буровых работ можно воспроизвести путем изучения отношения приложенной МУЭ к ППС [10, 23, 24]. Приложение избыточной энергии может привести к многочисленным проблемам, включая вибрации в бурильной колонне, повышенный износ долота и снижение скорости проходки. Поэтому баланс приложенной МУЭ и ППС породы имеет решающее значение для обеспечения оптимальной производительности бурения [28]. Исследования показали, что использование ПОС вместо ППС породы не дает верных результатов. Если бурение рассматривается в атмосферных условиях, значение МУЭ коррелирует с ПОС породы. Однако в реальных условиях бурения значение МУЭ приближается к ППС породы и, как правило, намного выше, чем ПОС породы. Поэтому оптимальные условия для буровых работ достигаются, когда вся энергия идет на разрушение горной породы, без заметных потерь энергии или неэффективного бурения [4, 17, 29], а прочность горной породы служит эталонным параметром для расчета энергии, затраченной на бурение [18, 19, 30]. Исходя из этого, механическую производительность буровых работ можно представить следующим образом:
Обычно, когда МУЭ приближается к пределу прочности породы на сжатие, механическая производительность увеличивается [23, 24, 27]. Одна из широко распространенных формул в механике горных пород для расчета ППС выведена на основе принципа Терцаги и критерия Мора – Кулона [10]:
где φ – угол внутреннего трения породы; ∆Д – дифференциальное давление между давлением бурового раствора и поровым давлением.
Для расчета ПОС на основе литологического состава пород предлагаются различные эмпирические формулы. В табл.1 показано несколько общих формул расчета ПОС для карбонатных, известняковых и доломитовых пород.
Таблица 1
Уравнения для расчета ПОС горных пород [31-33]
|
Литологический состав пласта |
Исследователи |
Уравнение |
Требуемые параметры |
|
Карбонат |
Режевский, Новик (1971) |
|
Пористость |
|
Известняк |
Милитцер, Столл (1973) |
|
Скорость продольных волн |
|
Голубев, Рабинович (1976) |
|
||
|
Карбонат |
Сарда и др. (1993) |
|
Пористость |
|
Фаркухар и др. (1994) |
|
||
|
Известняк, доломит, мергель, песчаник, гематит, туф, диабаз |
Кристарас и др. (1997) |
|
Скорость продольных волн |
|
Карбонат |
Эдиманн и др. (1998) |
|
Пористость |
|
Ясар и др. (2004) |
|
Скорость продольных волн |
|
|
Известняк, доломит |
Чантдун и др. (2006) |
|
Время распространения продольных волн |
|
Карбонат |
|
||
|
Известняк |
|
Динамический модуль Юнга |
|
|
Доломит |
|
||
|
Карбонат |
|
Пористость |
|
|
|
|||
|
Известняк |
Амин и др. (2007) |
|
|
|
Доломит |
|
||
|
Карбонатная порода с прослоями сланца |
Афсари и др. (2010) |
|
Статический модуль Юнга |
|
Карбонат |
Амани и др. (2013) |
|
Время распространения продольных волн |
|
|
Время распространения продольных волн и пористость |
||
|
Карбонат |
Наджиби и др. (2015) |
|
Статический модуль Юнга |
|
|
Динамический модуль Юнга |
||
|
|
Скорость продольных волн |
Как показано в табл.1, модуль Юнга требуется для расчета ПОС во многих уравнениях. Кроме того, согласно уравнению (7), для расчета ППС требуется угол внутреннего трения. В табл.2 представлены общие эмпирические соотношения для расчета модуля Юнга и угла внутреннего трения [34-36].
Таблица 2
Эмпирические уравнения для расчета модуля Юнга [34-36] и угла внутреннего трения [37-39]
|
Литологический состав пласта |
Исследователи |
Уравнение |
Требуемые параметры |
|
Расчет модуля Юнга |
|||
|
Карбонат
|
Эйсса и др. (1988) |
|
Динамический модуль Юнга |
|
|
Динамический модуль Юнга, плотность |
||
|
Эдиманн и др. (1998) |
|
Пористость |
|
|
Доломит |
Амин и др. (2007) |
|
|
|
Известняк |
|
||
|
Общий |
Фьяер и др. (2008) |
|
Плотность, скорость продольных волн, скорость поперечных волн |
|
Карбонат |
Афсари и др. (2010) |
|
Динамический модуль Юнга |
|
Асмари и Сарвак |
Наджиби и др. (2015) |
|
|
|
|
Скорость продольных волн |
||
|
Расчет угла внутреннего трения |
|||
|
Известняк |
Эдиманн (1998) |
|
Пористость |
|
Карбонат |
Арчер и др. (2012) |
|
Пористость, объем сланца |
В рамках настоящего исследования сначала были собраны и обработаны данные, а также разработана оптимальная модель МУЭ для изучаемого месторождения, затем определены зоны неэффективного бурения путем сравнения МУЭ с ППС породы. Кроме того, проанализированы соотношения между различными буровыми параметрами для формирования выводов об оптимизации управляемых переменных бурения.
Необходимые буровые данные были собраны и обработаны на первом этапе. Затем буровые данные были использованы в оптимальной модели МУЭ. Кроме того, данные, полученные из петрофизических журналов, были извлечены и обработаны с помощью программного обеспечения Geolog. После внесения необходимых исправлений в исходные журнальные данные они были сгруппированы и классифицированы для оценки ППС. Наконец, мы сравнили рассчитанные значения МУЭ и ППС, чтобы сделать вывод о производительности бурового процесса.
Месторождение, рассматриваемое в настоящем исследовании – одно из крупнейших континентальных нефтяных месторождений Ирана. Оно расположено в юго-западной части страны, общая глубина 4130 м. Данные для исследования были извлечены из отчетов по одной из скважин – ежедневных отчетов по бурению, журналов проб бурового раствора, буровых и петрофизических журналов.
В исследуемой скважине данные каротажа доступны только по разрезу коллектора свиты Асмари, т.е. в диапазоне глубин от 3840 до 4100 м. Поэтому исследование ограничено этим диапазоном глубин, поскольку для расчета ППС необходимы данные каротажа. Свита Асмари, как основной коллектор на месторождении, подразделяется на шесть отдельных слоев, в основном состоящих из доломитовых карбонатов, сланца и мергеля.
После сбора буровых данных был проведен их статистический анализ для лучшего понимания и выявления выбросов и неинформативных значений. В табл.3 представлены результаты описательной статистики буровых параметров.
Таблица 3
Описательный статистический анализ буровых параметров
|
Статистические показатели |
ННД, кН |
КМ, кН·м |
СВ, об/мин |
СП, м/ч |
Р, м3/с |
ПБР, кг/м3 |
|
Среднее значение |
7702,5 |
1949,6 |
160,6 |
10,8 |
458,2 |
9 |
|
Медиана |
7204,5 |
2032,2 |
176,2 |
10,6 |
456 |
9,1 |
|
Мода |
0 |
0 |
0 |
15,6 |
0 |
9,1 |
|
Стандартное отклонение |
3425,5 |
325 |
35,9 |
6,7 |
18,8 |
0,2 |
|
Дисперсия |
11733791,8 |
105650 |
1291,1 |
44,8 |
353,1 |
0,03 |
|
Минимум |
1719,4 |
942,7 |
55,4 |
1,6 |
368,3 |
7,5 |
|
Максимум |
22642,1 |
2539,3 |
185,6 |
95,1 |
511,3 |
9,5 |
Каротажные данные также собирались и сортировались в программном обеспечении Geolog. Особенности данных исследуемой скважины по типам каротажа (верхняя глубина каротажа 3840 м; нижняя глубина – 4115 м; шаг каротажа 0,1 м): CALI – диаметр скважины; PE – фотоэлектрический фактор; HDRS – глубинное сопротивление; HMRS – среднее удельное сопротивление; NPHI – нейтронный каротаж; RHOB – плотность; DRHO – исправленная плотность; POTA – калий; THOR – торий; URAN – уран; SGR – гамма-каротаж с элементами тория и калия; CGR – гамма-каротаж с элементами тория, калия и урана; GR – гамма-каротаж; DT – время пробега продольной волны.
Буровые и каротажные данные обычно собирают с помощью специальных датчиков, поэтому в них могут быть ошибки, т.е. значения, которые следует удалить из базы данных. Например, из-за осевых колебаний бурильной колонны могут быть зарегистрированы значения ННД, намного превышающие допустимый предел (учитывая ограничения, связанные с размером и типом долота и длиной бурильной колонны). Важно удалить такие выбросы из базы данных. Выбросы – наблюдения, которые численно далеки от других данных наблюдений. Для этого существует несколько методов. В настоящем исследовании для удаления статистических выбросов был применен метод диаграммы размаха («ящик с усами»). Диаграмма размаха – очень полезный инструмент для анализа данных, обеспечивающий графическое представление распределения данных, позволяющий интуитивно сравнивать статистические параметры. Эта диаграмма позволяет наглядно увидеть дисперсию и асимметрию данных. Кроме того, диаграмма размаха дает возможность идентифицировать области с более высокой или низкой концентрацией данных [40, 41]. При рассмотрении диаграммы размаха точки, находящиеся за пределами нижней и верхней граничных линий, определяются как выбросы.
В данном исследовании с использованием буровых и каротажных данных были рассчитаны и сопоставлены общепринятые модели МУЭ – Тила, Пессье и Фира, Дюпри и Кедерица, УЭБ и УГМЭ. Согласно модели Тила, на МУЭ влияют такие параметры, как нагрузка на долото, площадь долота, скорость вращения, крутящий момент и скорость проходки. В модели Пессье и Фира МУЭ рассчитывалась с использованием стандартного значения коэффициента трения скольжения, предложенного М.Арментой, для типов долот, используемых в исследуемой скважине. Исходя из этого, для интервалов глубины, где использовались штыревые долота, рассматривалось значение коэффициента трения 0,25, а для интервалов, где использовались долота с поликристаллическими алмазными резцами, применялось значение коэффициента трения 0,5.
В уточненной модели Дюпри и Кедерица МУЭ рассчитывалась по уравнению (4). В модель в качестве важного параметра была включена механическая производительность бурения, равная 0,35, в соответствии с предложением Дюпри и Кедерица. Однако можно рекомендовать применение других значений в различных геологических и эксплуатационных условиях.
Для расчета УЭБ использовалась формула (5) [10, 11, 15], представленная М.Арментой, в которой в дополнение к буровым параметрам, упомянутым в первоначальной модели Тила, удельная энергия бурения зависит от других критически важных параметров, которые игнорировались в предыдущих моделях, а именно от расхода и веса бурового раствора. Кроме того, коэффициент влияния гидравлики долота был определен как 0,018 [12].
Полная модель УГМЭ была рассчитана с использованием уравнения (6). Эта модель включает все энергетические компоненты – осевую, вращательную и гидравлическую энергии бурового раствора. Помимо буровых параметров в модель также были введены градиент порового давления и эквивалентная плотность циркуляции.
Что касается литологического состава исследуемой свиты, для оценки механических и прочностных свойств породы был использован набор эмпирических уравнений (табл.4). Эти уравнения также применялись для расчета скоростей продольных и поперечных волн. Литологический состав свиты Асмари был определен с помощью сводного графика нейтронной плотности (рис.1), где нижняя (плотность 2,6 г/см3), средняя (плотность 2,71 г/см3) и верхняя линии (плотность 2,87 г/см3) относятся к песчанику, известняку и доломиту соответственно. Программное обеспечение Geolog определяет и строит эти линии с помощью инструмента нейтронного каротажа (Dual Spaced Neutron II), который применялся в исследуемой скважине. Учитывая распределение точек между линиями плотности известняка и доломита, литологический состав свиты Асмари попадает в карбонатную группу, что указывает на сочетание известняка и доломита.
Таблица 4
Эмпирические уравнения для определения механических и прочностных свойств горных пород [34, 35, 38]
|
Параметр |
Уравнение |
Исследователи |
|
Угол внутреннего трения |
|
Арчер и Расули (2012) |
|
Скорость продольных волн |
|
– |
|
Скорость поперечных волн |
|
Кастанья (1985) |
|
Динамический модуль Юнга |
|
Фьяер и др. (2008) |
|
Статический модуль Юнга |
|
Наджиби и др. (2015) |
|
Неограниченная прочность на сжатие |
|
Наджиби и др. (2015) |
|
Ограниченная прочность на сжатие |
|
Кайседо и др. (2005) |
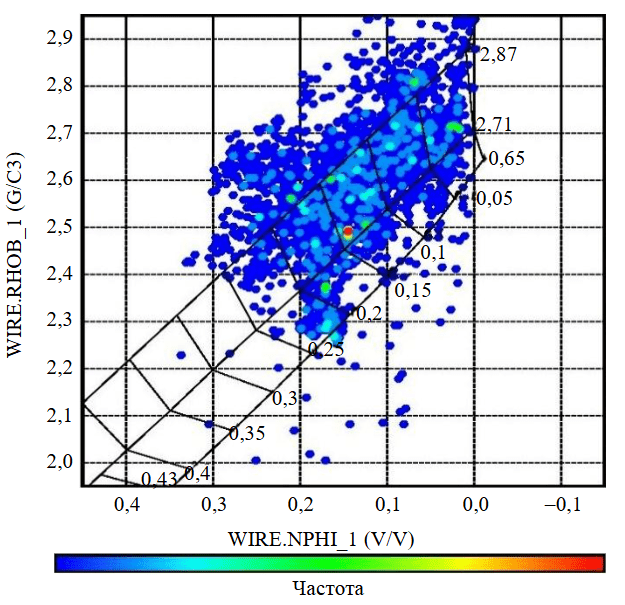
Рис.1. Зависимость нейтронной плотности от литологического состава
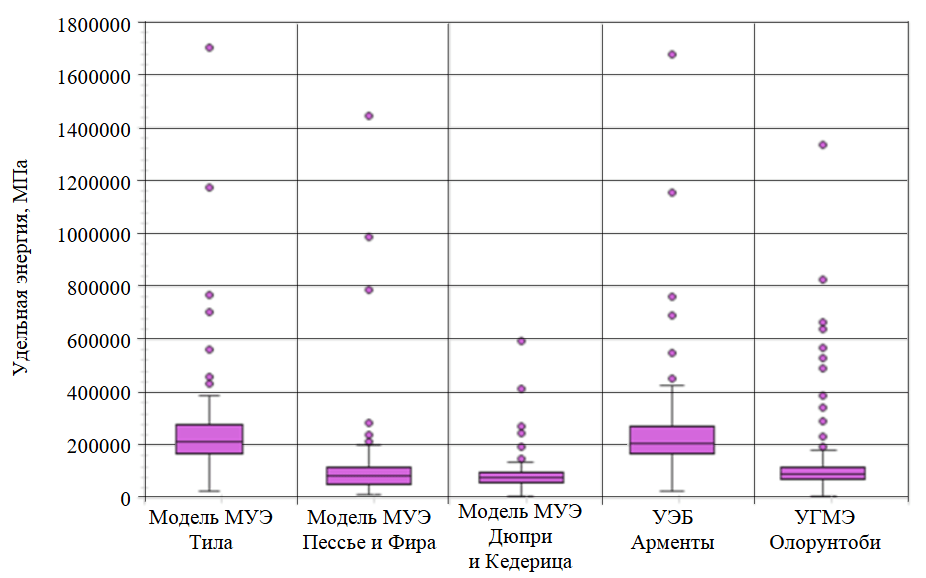
Рис.2. Статистические выбросы для моделей МУЭ
Обсуждение
Когда МУЭ приближается к ППС породы, она находится в оптимальном диапазоне, что указывает на корректный выбор управляемых параметров бурения. В данном разделе представлен подробный анализ собранных данных с особым вниманием к оценке значений МУЭ и их изменению с глубиной. Такое всестороннее понимание буровых условий имело решающее значение для эффективности операций. Затем путем сравнения расчетных значений МУЭ по стволу скважины и их оптимального значения (равного ППС породы) были определены зоны неэффективного бурения. После этого была проанализирована связь между МУЭ, скоростью проходки и другими буровыми параметрами для более точного описания буровых условий в исследуемой скважине.
После сбора буровых данных модели МУЭ были рассчитаны с использованием уравнений (2)-(6), а затем по методу диаграммы размаха были удалены выбросы. На рис.2 показана диаграмма размаха для выявления выбросов в рассчитанных значениях МУЭ. Точки данных, расположенные значительно выше или значительно ниже диаграммы, являются выбросами. Согласно рис.2, наибольшее количество выбросов было в моделях МУЭ, рассчитанных по Тилю, Пессье и Фиру, а также УЭБ. В табл.5 приведены верхняя и нижняя границы, первый и третий квартили, общее количество точек и точки выбросов для моделей МУЭ.
Таблица 5
Нижние и верхние границы для моделей МУЭ и количество выбросов, МПа
|
Характеристика |
Модель МУЭ |
||||
|
Тила |
Пессье и Фир |
Дюпри и Кедериц |
УЭБ |
УГМЭ |
|
|
Первый квартиль |
171132,9 |
55558,7 |
59896,5 |
167835,2 |
72126,8 |
|
Третий квартиль |
275714,1 |
118843,4 |
96499,9 |
271835,4 |
119711 |
|
Нижняя граница |
14261,1 |
39368,3 |
4991,4 |
11834,9 |
750,5 |
|
Верхняя граница |
432585,9 |
213770,5 |
151405,1 |
427835,7 |
191087,4 |
|
Всего точек |
261 |
261 |
261 |
261 |
261 |
|
Точек выбросов |
12 |
7 |
12 |
11 |
30 |
|
Оставшиеся точки |
249 |
254 |
249 |
250 |
231 |
Изменения МУЭ в зависимости от глубины нанесены на график (рис.3) как с удалением выбросов, так и без него. Из графика видно, что значения МУЭ из моделей Тила и УЭБ очень близки друг к другу, почти полностью совпадая. В моделях Пессье и Фира, Дюпри и Кедерица, а также УГМЭ значения МУЭ более низкие, что указывает на лучшие условия.
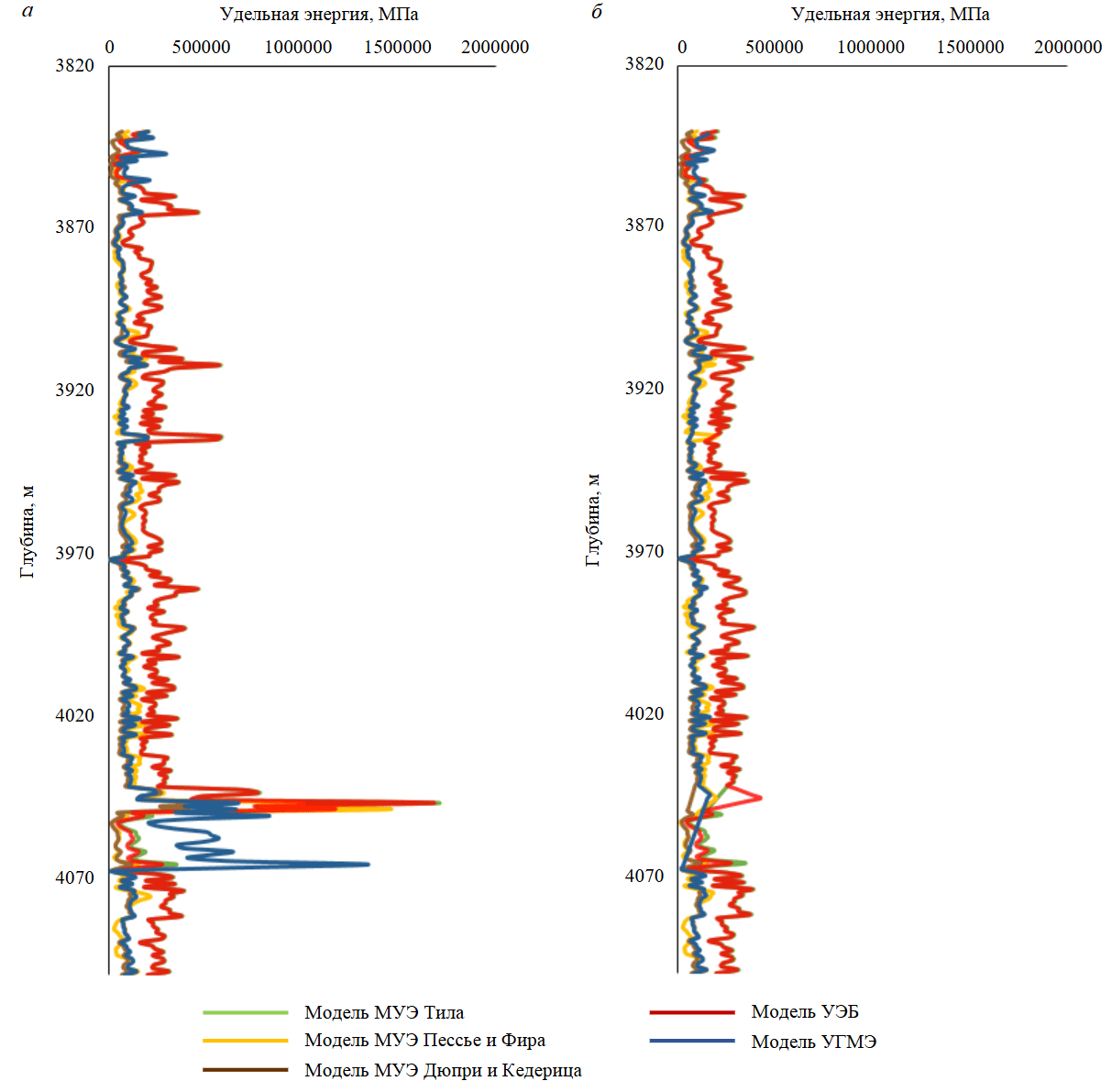
Рис.3. МУЭ в зависимости от глубины: а – с выбросами; б – выбросы удалены
Модель УГМЭ включает все компоненты энергии, т.е. осевую, вращательную и гидравлическую энергии, обеспечивая более точное представление приложенной поверхностной энергии по сравнению с другими моделями. С другой стороны, как видно на рис.3, модель Дюпри и Кедерица обеспечивает лучшее представление МУЭ по сравнению с другими моделями благодаря коэффициенту механической производительности. Поэтому в данном исследовании предложена следующая комбинация этих двух моделей для расчета МУЭ в исследуемой скважине:
МУГМЭ, разработанная в данном исследовании, это специальная модель МУЭ, которая учитывает как влияние механической производительности, так и факторы гидравлической энергии. МУГМЭ имеет наименьшее возможное значение по сравнению с другими моделями МУЭ, обеспечивая оптимальное представление приложенной поверхностной энергии. На рис.4 показаны неограниченная и ограниченная прочности породы на сжатие (рис.4, а), статический и динамический модуль Юнга (рис.4, б), скорости сдвиговых и продольных волн (рис.4, в), угол внутреннего трения (рис.4, г). ППС сравнивается с МУГМЭ для определения зон, где бурение считается неэффективным.
После определения значений МУГМЭ и ППС породы эти значения были нанесены на график вместе с другими буровыми параметрами свиты Асмари для сравнения значений удельной энергии с диаграммой прочности породы на сжатие с целью выявления проблемных зон (рис.5). На определенных глубинах в скважине буровые параметры претерпели резкие изменения, и влияние этих изменений на МУГМЭ весьма заметно. В диапазоне глубин от 4043 до 4068 м скорость бурения снизилась, что сопровождалось снижением скорости вращения и крутящего момента и увеличением скорости расхода буровой жидкости. В частности, скорость бурения снизилась от 2,7 до 0,3 м/ч, скорость вращения снизилась от 180 до 70 об/мин, а крутящий момент упал от 2711 до 1627 Н·м, в то время как расход буровой жидкости увеличился от 0,028 до 0,031 м3/с. Эта зона обозначена серым цветом. В данном диапазоне глубин удельная энергия внезапно увеличилась по сравнению с прочностью породы на сжатие, что сопровождалось снижением скорости проходки. Поэтому зона была определена как проблемная.
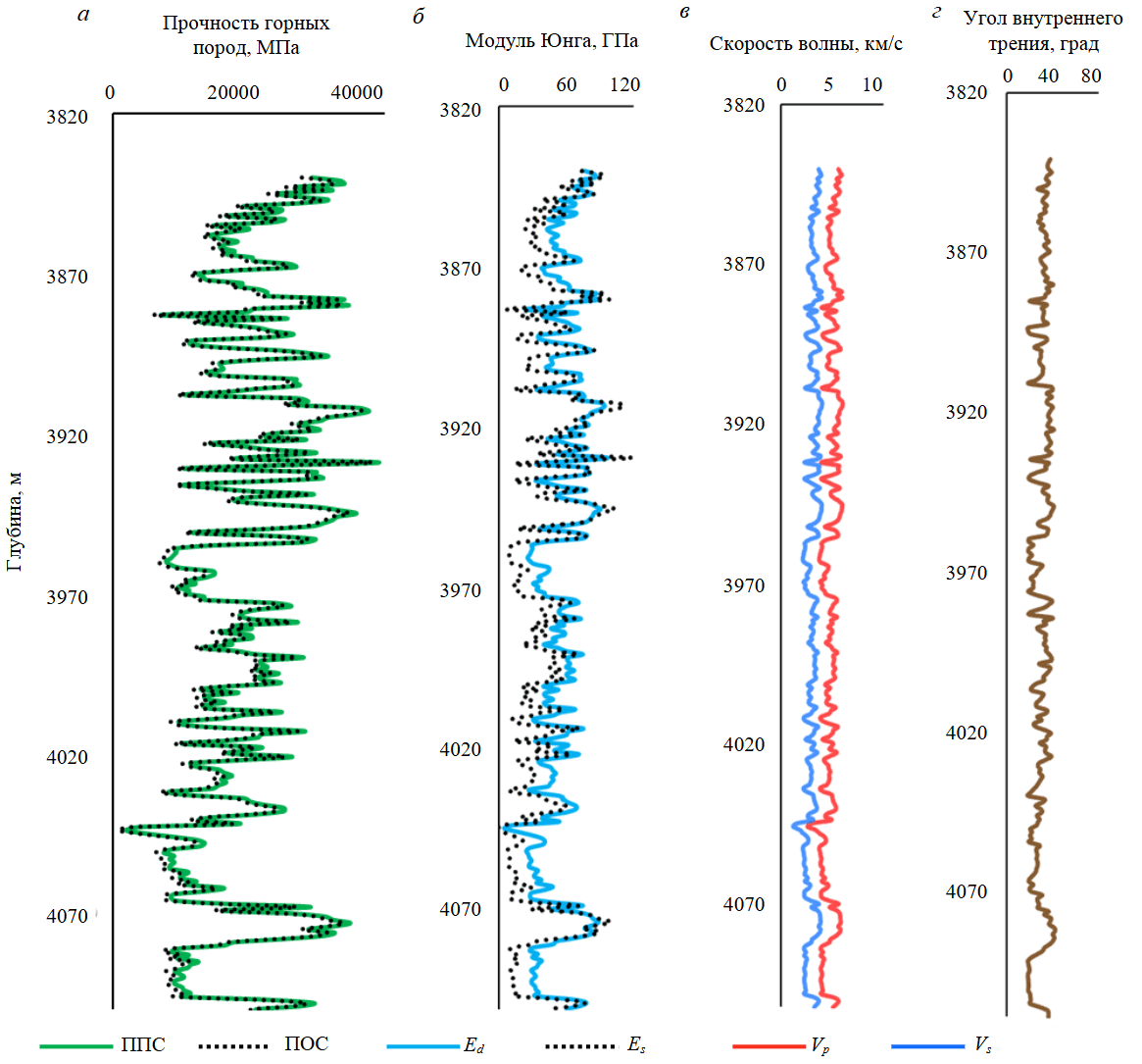
Рис.4. Механические и прочностные свойства горных пород в исследуемой скважине
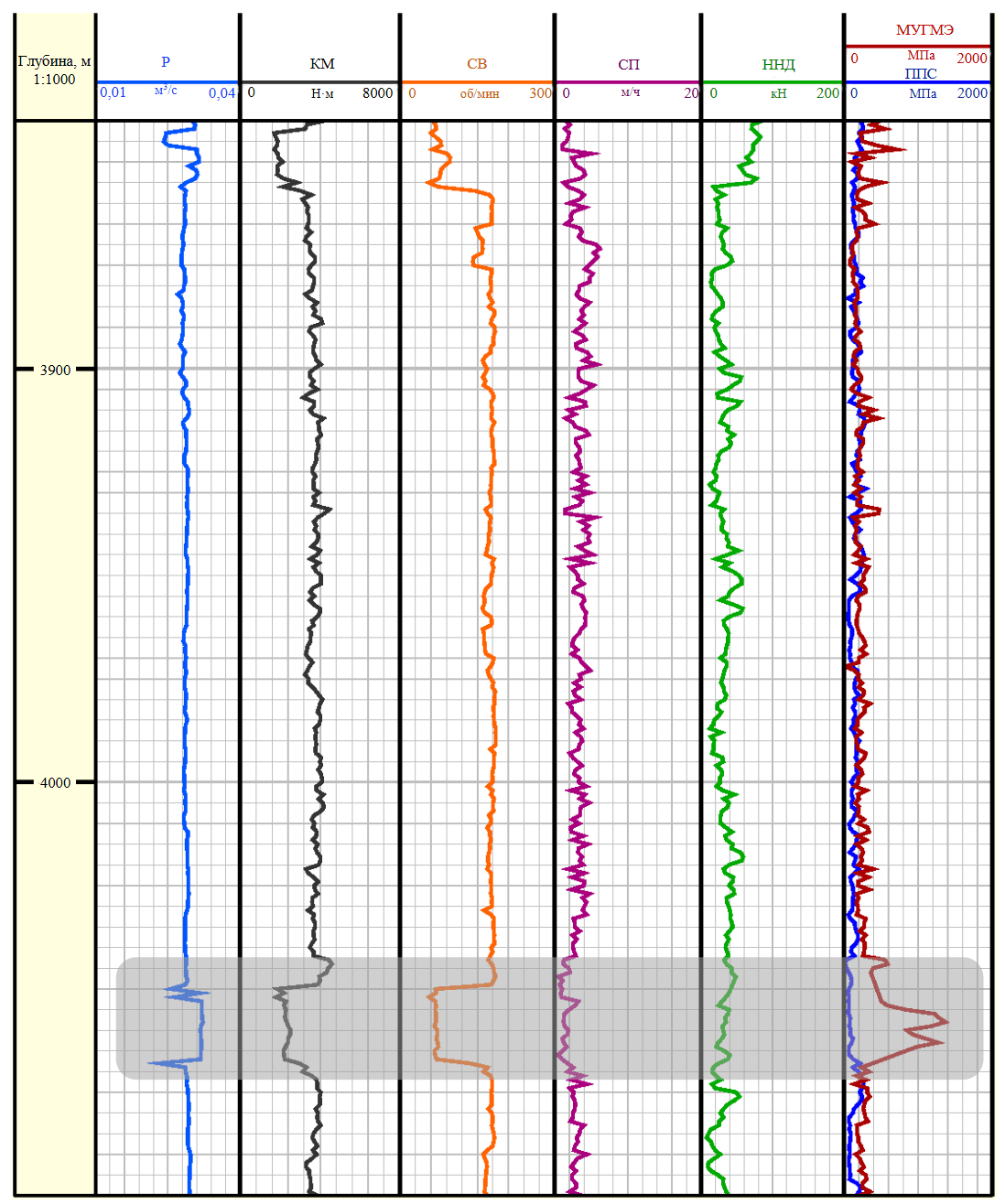
Рис.5. Оценка и анализ МУЭ и ППС породы в исследуемой скважине
Для детального анализа наблюдаемых результатов были изучены отчеты по бурению для этого диапазона глубин. Отмечалось, что из-за чрезмерно приложенной энергии, превышающей прочность горной породы, буровое долото получило значительные повреждения: семь резцов долота с поликристаллическими алмазными элементами были потеряны, а десять резцов сломаны. При эффективных буровых операциях вся приложенная поверхностная энергия расходуется на разрушения горной породы, т.е. увеличение поверхностной энергии должно приводить к увеличению скорости проходки. В противном случае это означает, что приложенная энергия была потрачена впустую на вибрации, колебания и износ бурового долота.
Для дальнейшего анализа исследуемой скважины была изучена связь управляемых буровых параметров со скоростью проходки и МУГМЭ. На рис.6 показано изменение скорости проходки в зависимости от нагрузки на долото и частоты вращения. В эффективном бурении при увеличении нагрузки на долото осевое усилие на долото должно увеличивать скорость проходки до достижения порогового значения нагрузки. Однако из рис.6 видно, что увеличение нагрузки на долото не привело к значительному увеличению скорости проходки, а в какой-то момент скорость проходки даже снизилась. Следовательно, увеличение нагрузки на долото в этой скважине не способствовало повышению производительности бурения и привело к большему износу долота. Серым цветом обозначена проблемная зона, где увеличение нагрузки на долото от 26 до 35 кН приводит к снижению скорости проходки.
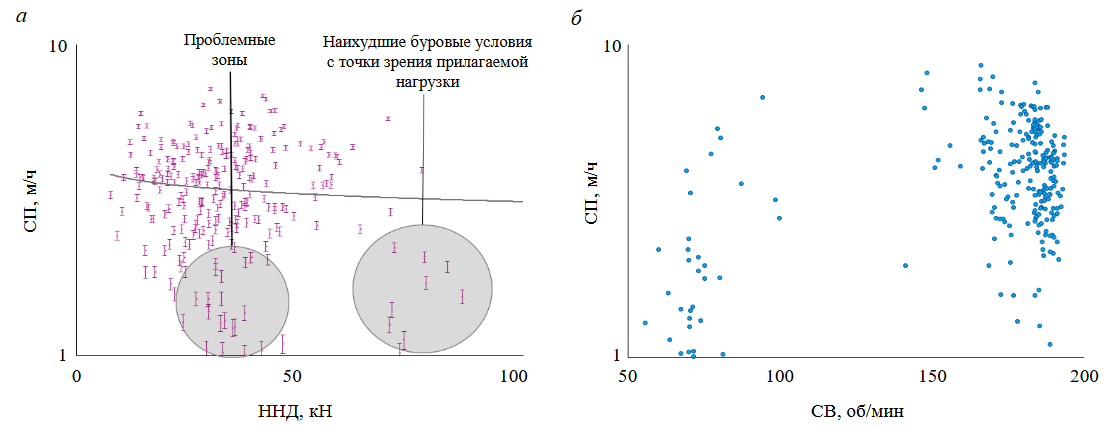
Рис.6. Скорость проходки в зависимости от нагрузки на долото (а) и частоты вращения (б)
В оптимизированных операциях между скоростью вращения бурильной колонны и скоростью проходки должна быть прямая связь. Однако, как видно из рис.6, в исследуемой скважине нет существенной связи между скоростью вращения и скоростью проходки. Увеличение скорости вращения может привести к существенному приложению энергии, проявляющемуся в виде вибраций в бурильной колонне. Это может повлечь повреждение долота, увеличение крутящего момента и повышение удельной механической энергии, в конечном итоге не обеспечивая оптимальных буровых условий. Для определения оптимальной скорости вращения нагрузка на долото должна поддерживаться постоянной при изменении скорости вращения. Наблюдая за изменениями скорости проходки и МУЭ, можно определить оптимальную скорость вращения, где ее увеличение сопровождается заметным увеличением скорости проходки.
Другим управляемым параметром, влияющим на скорость проходки и МУЭ, является расход бурового раствора, закачиваемого в скважину. Буровой раствор с оптимальным расходом способствует удалению шлама из-под долота, его транспортировке из скважины на поверхность и увеличению скорости проходки. В исследуемой скважине расход оставался относительно постоянным на уровне около 0,028-0,029 м3/с.
На рис.7, a показаны МУГМЭ и ППС породы при различных скоростях проходки, на основании которых были определены зоны эффективного и неэффективного бурения в исследуемой скважине. Верхняя левая часть рисунка соответствует зоне неэффективного бурения, где приложенная поверхностная энергия намного выше, чем ППС породы. Это означает, что увеличение энергии не привело к увеличению скорости проходки. Нижний правый угол рисунка соответствует эффективной зоне бурения, где МУГМЭ ближе к ППС породы. Это означает, что увеличение потребляемой энергии привело к увеличению скорости проходки. Между ними находится переходная зона от неэффективного к эффективному бурению.
Рис.7, б иллюстрирует связь между скоростью проходки и нагрузкой на долото. В диапазоне от 22,24 до 44,48 кH ННД скорость проходки приближается примерно к 6,1 м/ч. При этой скорости проходки МУГМЭ падает ниже 344,73 МПа. Это обоснованный результат, поскольку значение МУГМЭ ближе к ППС породы, что подразумевает эффективность буровых операций.
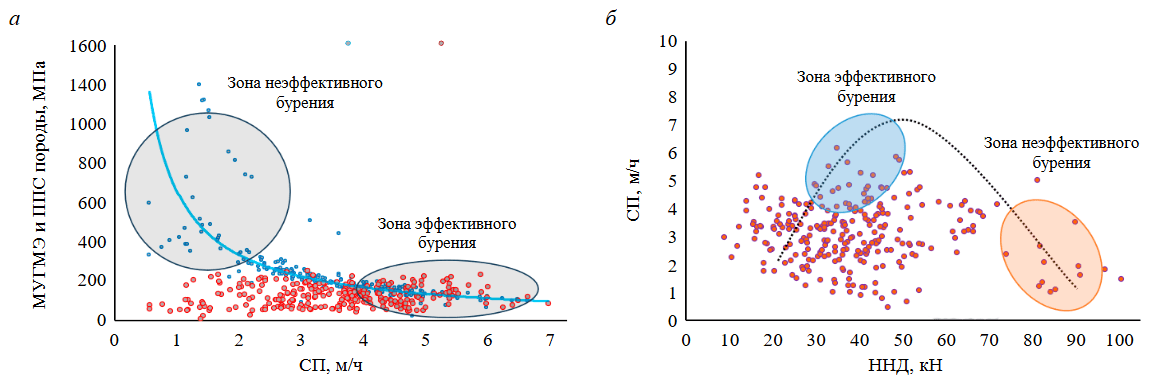
Рис.7. Сравнение МУГМЭ и ППС со скоростью проходки (а) и скорости проходки с ННД (б) с определением зон эффективного и неэффективного бурения
При анализе взаимосвязи между буровыми параметрами можно сделать вывод, что оптимальные диапазоны для нагрузки на долото, расхода бурового раствора, крутящего момента и скорости вращения составляют от 22,24 до 44,48 кH, от 0,027 до 0,029 м3/с, от 2522 до 3091 Н·м и от 160 до 180 об/мин соответственно. Оптимальные значения были выбраны таким образом, чтобы минимизировать МУГМЭ, сохраняя при этом скорость проходки. Также в исследуемой скважине была выявлена зона неэффективного бурения, где приложение избыточной поверхностной энергии по сравнению с прочностью породы привело к повреждению бурового долота.
Заключение
Оптимизация бурового процесса важна, поскольку снижает общую стоимость скважины. Существует несколько подходов к оптимизации бурения, в данной работе рассматривается концепция удельной механической энергии. При использовании реальных полевых данных были проверены некоторые общепринятые модели МУЭ и разработана новая модель МУЭ. Сравнение значений МУЭ из новой модели с прочностью горных пород может привести к повышению производительности бурения. На базе проведенных исследований можно сделать следующие основные выводы:
- Разработана измененная модель МУЭ для исследуемой скважины. По сравнению с предыдущими моделями измененная модель дает значения удельной энергии ближе к ППС. Измененная модель учитывает влияние таких параметров как нагрузка на долото, скорость проходки, расход бурового раствора и коэффициент механической производительности.
- В исследуемой скважине рассчитанное оптимальное значение МУГМЭ составило менее 206,84 МПа, так как в этом диапазоне глубин значения удельной механической энергии были близки к прочности породы пласта.
- Оптимальные диапазоны нагрузки на долото, расхода бурового раствора, крутящего момента и скорости вращения были определены как 22,24-44,48 кH, 0,027-0,029 м3/с, 2522-3091 Н·м и 160-180 об/мин соответственно. С применением оптимизированных значений получено снижение МУГМЭ, при котором скорость проходки достигает 4,57-6,1 м/ч.
- Применение высокой нагрузки на долото, т.е. свыше 66,72 кH, значительно снижает скорость проходки (до 1,52 м/ч). При этом МУЭ выходит за пределы оптимального диапазона, превышая 344,73 МПа. Это происходит потому, что применение повышенных значений нагрузки на долото приводит к его износу, вызывающему снижение скорости проходки.
Литература
- Weiqiang Song, Huidong Mu, Wenjuan Ji et al. Evaluation and optimization of drilling efficiency while drilling based on improved rock-breaking specific energy model of bit // Geomechanics and Geophysics for Geo-Energy and Geo-Resources. 2024. Vol. 10. Iss. 1. № 174. DOI: 10.1007/s40948-024-00872-9
- Kunshin A., Dvoynikov M., Timashev E., Starikov V. Development of Monitoring and Forecasting Technology Energy Efficiency of Well Drilling Using Mechanical Specific Energy // Energies. 2022. Vol. 15. Iss. 19. № 7408. DOI: 10.3390/en15197408
- Mantegazini D.Z., Nascimento A., Dornelas V.F. et al. Analysis and Multi-Objective Optimization of the Rate of Penetration and Mechanical Specific Energy: A Case Study Applied to a Carbonate Hard Rock Reservoir Based on a Drill Rate Test Using Play-Back Methodology // Applied Sciences. 2024. Vol. 14. Iss. 6. № 2234. DOI: 10.3390/app14062234
- Khalilidermani M., Knez D. A Survey of Application of Mechanical Specific Energy in Petroleum and Space Drilling // Energies. 2022. Vol. 15. Iss. 9. № 3162. DOI: 10.3390/en15093162
- Mohammadi Behboud M., Ramezanzadeh A., Tokhmechi B. et al. Estimation of geomechanical rock characteristics from specific energy data using combination of wavelet transform with ANFIS-PSO algorithm // Journal of Petroleum Exploration and Production Technology. 2023. Vol. 13. Iss. 8. P. 1715-1740. DOI: 10.1007/s13202-023-01644-z
- Oloruntobi O., Butt S. Energy-based formation pressure prediction // Journal of Petroleum Science and Engineering. 2019. Vol. 173. P. 955-964. DOI: 10.1016/j.petrol.2018.10.060
- Oloruntobi O., Butt S. Application of specific energy for lithology identification // Journal of Petroleum Science and Engineering. 2020. Vol. 184. № 106402. DOI: 10.1016/j.petrol.2019.106402
- Leusheva E.L. Evaluation of Possible Application of Powder Made from Fallen Tree Leaves as a Drilling Mud Additive // International Journal of Engineering – Transactions B: Applications. 2024. Vol. 37. Iss. 8. P. 1592-1599. DOI: 10.5829/ije.2024.37.08b.12
- Leusheva E., Brovkina N., Morenov V. Investigation of Non-Linear Rheological Characteristics of Barite-Free Drilling Fluids // Fluids. 2021. Vol. 6. Iss. 9. № 327. DOI: 10.3390/fluids6090327
- Zamanzadeh Talkhouncheh M., Davoodi S., Wood D.A. et al. Robust Machine Learning Predictive Models for Real-Time Determination of Confined Compressive Strength of Rock Using Mudlogging Data // Rock Mechanics and Rock Engineering. 2024. Vol. 57. Iss. 9. P. 6881-6907. DOI: 10.1007/s00603-024-03859-w
- Dupriest F.E., Witt J.W., Remmert S.M. Maximizing ROP With Real-Time Analysis of Digital Data and MSE // International Petroleum Technology Conference, 21-23 November 2005, Doha, Qatar. OnePetro, 2005. № IPTC-10607-MS. DOI: 10.2523/IPTC-10607-MS
- Armenta M. Identifying Inefficient Drilling Conditions Using Drilling-Specific Energy // SPE Annual Technical Conference and Exhibition, 21-24 September 2008, Denver, CO, USA. OnePetro, 2008. № SPE-116667-MS. DOI: 10.2118/116667-MS
- Rafatian N., Miska S., Ledgerwood L.W. et al. Experimental Study of MSE of a Single PDC Cutter Interacting With Rock Under Simulated Pressurized Conditions // SPE Drilling & Completion. 2010. Vol. 25. Iss. 1. P. 10-18. DOI: 10.2118/119302-PA
- Thomson I.J., Mathur R. The Use of Downhole Drilling Parameters Combined With Surface and Downhole Mechanical Specific Energy Data Helped Identify Under-Reamer Dysfunctions in GoM Deepwater Projects // SPE Deepwater Drilling and Completions Conference, 5-6 October 2010, Galveston, TX, USA. OnePetro, 2010. № SPE-137139-MS. DOI: 10.2118/137139-MS
- Hammoutene C., Bits S. FEA Modelled MSE/UCS Values Optimise PDC Design for Entire Hole Section // North Africa Technical Conference and Exhibition, 20-22 February 2012, Cairo, Egypt. OnePetro, 2012. DOI: 10.2118/149372-MS
- Chao Xiong, Zhong-Wei Huang, Huai-Zhong Shi et al. Performances of a Stinger PDC cutter breaking granite: Cutting force and mechanical specific energy in single cutter tests // Petroleum Science. 2023. Vol. 20. Iss. 2. P. 1087-1103. DOI: 10.1016/j.petsci.2022.10.006
- Xuyue Chen, Xu Du, Chengkai Weng et al. A real-time drilling parameters optimization method for offshore large-scale cluster extended reach drilling based on intelligent optimization algorithm and machine learning // Ocean Engineering. 2024. Vol. 291. № 116375. DOI: 10.1016/j.oceaneng.2023.116375
- Mohan K., Adil F., Samuel R. Comprehensive Hydromechanical Specific Energy Calculation for Drilling Efficiency // Journal of Energy Resources Technology. 2015. Vol. 137. Iss. 1. № 012904. DOI: 10.1115/1.4028272
- Mohammadi Behboud M., Ramezanzadeh A., Tokhmechi B. Studying empirical correlation between drilling specific energy and geo-mechanical parameters in an oil field in SW Iran // Journal of Mining and Environment. 2017. Vol. 8. Iss. 3. P. 393-401. DOI: 10.22044/jme.2016.689
- Dvoynikov M., Kunshin A., Blinov P., Morozov V. Development of Mathematical Model for Controlling Drilling Parameters with Screw Downhole Motor // International Journal of Engineering – Transactions B: Applications. 2020. Vol. 33. Iss. 7. P. 1423-1430. DOI: 10.5829/ije.2020.33.07a.30
- Литвиненко В.С., Двойников М.В. Методика определения параметров режима бурения наклонно прямолинейных участков скважины винтовыми забойными двигателями // Записки Горного института. 2020. Т. 241. С. 105-112. DOI: 10.31897/PMI.2020.1.105
- Jinbo Song, Jianlong Wang, Bingqing Li et al. Real-Time Drilling Parameter Optimization Model Based on the Constrained Bayesian Method // Energies. 2022. Vol. 15. Iss. 21. № 8030. DOI: 10.3390/en15218030
- Khoshouei M., Bagherpour R. Measurement, prediction, and modeling of the drilling specific energy by soft rock properties during the drilling operation // Measurement. 2023. Vol. 222. № 113679. DOI: 10.1016/j.measurement.2023.113679
- Yavari H., Fazaelizadeh M., Aadnoy B.S. et al. An approach for optimization of controllable drilling parameters for motorized bottom hole assembly in a specific formation // Results in Engineering. 2023. Vol. 20. № 101548. DOI: 10.1016/j.rineng.2023.101548
- Menand S., Mills K. Use of Mechanical Specific Energy Calculation in Real-Time to Better Detect Vibrations and Bit Wear While Drilling // AADE National Technical Conference and Exhibition, 11-12 April 2017, Houston, TX, USA. American Association of Drilling Engineers, 2017. № AADE-17-NTCE-033.
- Ramba V., Selvaraju S., Subbiah S. et al. Optimization of drilling parameters using improved play-back methodology // Journal of Petroleum Science and Engineering. 2021. Vol. 206. № 108991. DOI: 10.1016/j.petrol.2021.108991
- Dupriest F., Lai S., Behounek M. et al. Standardization of Mechanical Specific Energy Equations and Nomenclature // SPE Drilling & Completion. 2023. Vol. 38. Iss. 1. P. 73-89. DOI: 10.2118/208777-PA
- Xuyue Chen, Deli Gao, Boyun Guo, Yongcun Feng. Real-time optimization of drilling parameters based on mechanical specific energy for rotating drilling with positive displacement motor in the hard formation // Journal of Natural Gas Science and Engineering. 2016. Vol. 35. Part A. P. 686-694. DOI: 10.1016/j.jngse.2016.09.019
- Song Deng, Shuo Yang, Yudie Chi et al. Bit optimization method for rotary impact drilling based on specific energy model // Journal of Petroleum Science and Engineering. 2022. Vol. 218. № 110977. DOI: 10.1016/j.petrol.2022.110977
- Kuilin Huang, Yingxin Yang, Gao Li et al. Torsion and vibration reduction mechanism of roller PDC hybrid bit // Journal of Petroleum Science and Engineering. 2022. Vol. 208. Part B. № 109491. DOI: 10.1016/j.petrol.2021.109491
- Verma A.K., Deb D., Dey A.C. et al. Development of one dimensional geomechanical model for a tight gas reservoir // Scientific Reports. 2021. Vol. 11. № 21433. DOI: 10.1038/s41598-021-00860-z
- Ye Liu, Shuming Liu, Jiafeng Zhang, Jie Cao. Real-time estimation of geomechanical characteristics using drilling parameter data and LWD // Geoenergy Science and Engineering. 2025. Vol. 244. № 213450. DOI: 10.1016/j.geoen.2024.213450
- Shijie Shen, Yanfang Gao, Lichun Jia. A Comparison of the Relationship between Dynamic and Static Rock Mechanical Parameters // Applied Sciences. 2024. Vol. 14. Iss. 11. № 4487. DOI: 10.3390/app14114487
- Abdul Aziz Q.A., Awadh S.M., Al-Mimar H.S. Estimation of Rock Mechanical Properties of the Hartha Formation and their Relationship to Porosity Using Well-Log Data // Iraqi Geological Journal. 2024. Vol. 57. № 1A. P. 34-44. DOI: 10.46717/igj.57.1A.4ms-2024-1-15
- Daraei A., Sharifi F., Qader D.N. et al. Prediction of the static elastic modulus of limestone using downhole seismic test in Asmari formation // Acta Geophysica. 2024. Vol. 72. Iss. 1. P. 247-255. DOI: 10.1007/s11600-023-01109-1
- Davarpanah S.M., Ván P., Vásárhelyi B. Investigation of the relationship between dynamic and static deformation moduli of rocks // Geomechanics and Geophysics for Geo-Energy and Geo-Resources. 2020. Vol. 6. Iss. 1. № 29. DOI: 10.1007/s40948-020-00155-z
- Almalikee H.S. Predicting Rock Mechanical Properties from Wireline Logs in Rumaila Oilfield, Southern Iraq // American Journal of Geophysics, Geochemistry and Geosystems. 2019. Vol. 5. № 2. P. 69-77.
- Zixu Wang, Junhong Huang, Yanglong Chen et al. Dynamic mechanical properties of different types of rocks under impact loading // Scientific Reports. 2023. Vol. 13. № 19147. DOI: 10.1038/s41598-023-46444-x
- Shahani N.M., Ullah B., Shah K.S. et al. Predicting Angle of Internal Friction and Cohesion of Rocks Based on Machine Learning Algorithms // Mathematics. 2022. Vol. 10. Iss. 20. № 3875. DOI: 10.3390/math10203875
- Rakhi, Gupta B., Lamba S.S. An efficient local outlier detection approach using kernel density estimation // Franklin Open. 2024. Vol. 8. № 100162. DOI: 10.1016/j.fraope.2024.100162
- Cangussu N., Milheiro-Oliveira P., Matos A.M. et al. Comparison of outlier detection approaches for compressive strength of cement-based mortars // Journal of Building Engineering. 2024. Vol. 95. № 110276. DOI: 10.1016/j.jobe.2024.110276
