Determination of the tangential component of cutting resistance during frozen sedimentary rock cutting using blocked, deeply blocked and cell cutting methods
- 1 — Ph.D., Dr.Sci. Professor Pacific National University ▪ Orcid
- 2 — Ph.D. Associate Professor Pacific National University ▪ Orcid ▪ Elibrary ▪ Scopus
Abstract
Due to the insufficient accuracy of existing studies of frozen sedimentary rock cutting process for practical calculations, the article solves the problem of determining the tangential component cutting resistance for blocked, deep blocked and cell cutting, which are currently the most commonly used methods in earthmoving equipment. The cutting tool and rock mass force interaction is considered from the point of view of the emerging stresses, which act on the separated chip element. The analytical dependences for determining the tangential component of cutting resistance were obtained. The numerical explanation of the choice of cell cutting in relation to blocked and deeply blocked cutting is given. For all three methods of cutting, under equal geometrical parameters of the cutting tool and the physical and mechanical properties of the frozen rock, the numerical value of the tangential component of cutting resistance is obtained. The comparison of the cutting resistance estimated values has shown that cell cutting requires relatively less energy and is preferred during the process of frozen sedimentary rock excavation. During field and laboratory investigations with the use of a multi-purpose cutting stand, a sufficient convergence of the analytical statements with the physics of frozen sedimentary rock cutting process was established. The results of the research allow a more reasonable approach to the adjustment of existing methods for determining the required tractive force and power for the drive of an excavation machine, and, therefore, to the actual efficiency and profitability of work.
Introduction
Most of the surface layer of the Russian Federation territory is covered with sedimentary rocks (clays, loams, sandy loams, sands), which are in a frost or permafrost state for 6-8 months a year due to the mountain climatic conditions [1]. Mining companies use a localized or major blast in order to destruct the frozen rock in quarry during winter [2]. Taking into consideration all costs of drilling and blasting operations, including the cost of explosives, storage buildings and their security, the transportation, the cost of the blasting and drilling equipment, the maintenance of explosives technicians and drillers, the downtime of the mining equipment while anticipating the blast and waiting for the explosion cloud dissipation, the estimated cost of a frozen rock layer destruction is rather high [3]. The increase in the cost of explosives and, in a number of instances, difficulties in their acquisition has led to the attempts to reject the drilling and blasting method. The other way is to use special machines, which work on the principle of mechanical destruction, specifically of loosening (cutting) [4, 5]. This category includes attached rippers on industrial tractors, excavators with milling equipment, ditch excavators (rotary or chain), surface miners, drilling machines, etc. [6, 7]. The mechanical method is not associated with conducting significant preparation works and makes it possible to use a number of mining machines designed primarily for the excavation of thawed rock along with the special earthmoving machines. The mechanical method of frozen rock excavation, which works on the cutting principle, predominates in the construction and mining industries [8, 9].
For more than seventy years, a pleiad of Russian scientists has been conducting research in the field of frozen rock cutting and excavating resistance [10, 11]. The studies by N.G.Dombrovsky, A.N.Zelenin, V.V.Abeshaus, M.I.Galperin, V.I.Balovnev, Yu.A.Vetrov, etc. have given a certain material for understanding the regular patterns of frozen rock cutting. However, the knowledge of the frozen rock cutting process still does not meet the current requirements of the industry when creating new equipment. The dependences for determining the rock cutting resistance are of an empirical nature and do not take the physics and the essence of cutting method into consideration [12-14]. There are discrepancies in determining the influence of rock hardness upon the cutting resistance [15]. The results of calculation using known empirical dependences of the cutting force tangential component represent a considerable divergence of values, while the maximum value exceeds the minimum value by 4.8 times [16-18].
The fundamental difference of the proposed method for determining the frozen sedimentary rock cutting resistance lies in its analytical nature with the further experimental verification of the results for the major cutting methods applied in practice: blocked, deeply blocked and cell cutting.
Methodology
The purpose of the study is to develop the analytical dependences for determining the tangential component of resistance to blocked, deeply blocked and cell cutting. The comparison of the numerical values of the cutting resistance tangential component for the given cutting methods, under equal geometrical parameters of the cutting tool and the frozen rock type, will allow determining the most effective rock excavation method from the point of view of energy intensity.
The scheme of blocked cutting is shown in Fig.1 [19]. During blocked cutting the separated chip elements have a complex shape (Fig.2) [19].
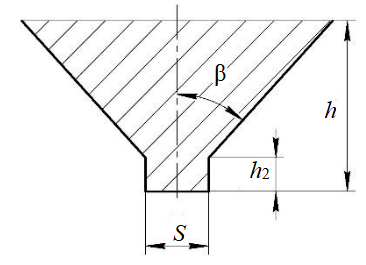
Fig.1. The scheme of slot section during the process of blocked cutting β – camber angle; S – cutting tool width; h – slot depth; h2 – slot bottom depth
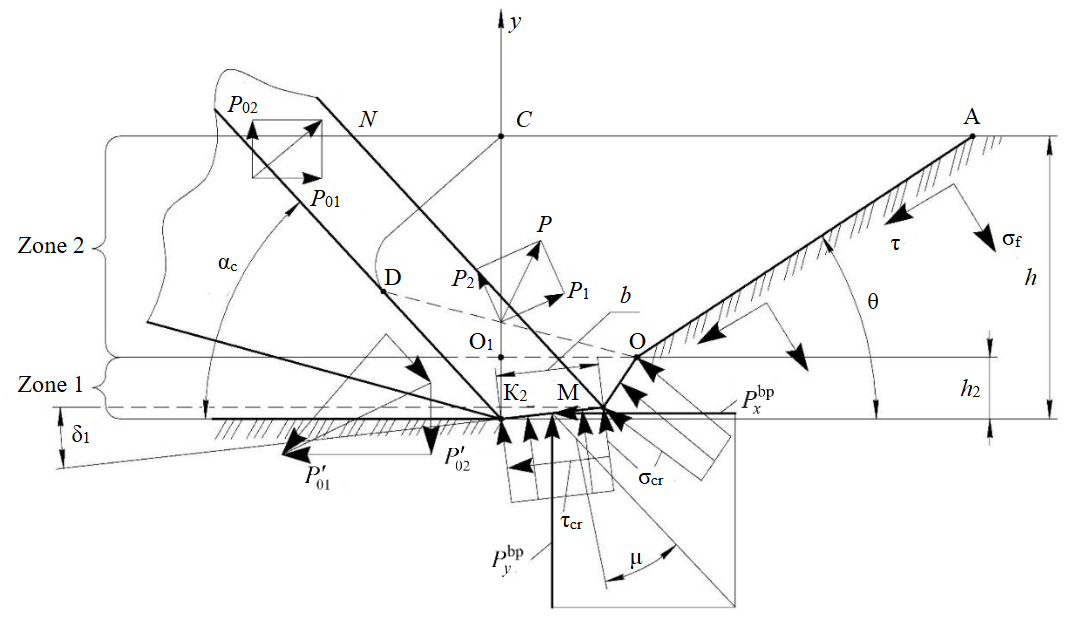
Fig.2. The calculation scheme of blocked cutting
With small assumptions, the chip element has a shape of a truncated cone half [20-22] with the depth (h – h2), bound by the surface ODC. The cutting tangential component Р01 can be determined while studying the chip element limit state before separation from the main rock mass [23]. The parameters of the cutting tool are: cutting angle αc, cutting edge angle 180°. Fracture stresses σf act normally on the separation surface, and shearing stresses τ act tangentially to the surface [24]. The stiff core is formed in the lower part (area h2S), therefore, the rock is crushed by the stresses σcr [25, 26].
This method considers cutting with teeth, in which the slot dimensions h, S, αc, h2 can vary in a wide range. The cutting was performed on coherent and incoherent frozen sedimentary rocks (loams and sand respectfully), which is taken into consideration in the dependences σf, τ, and σcr. During the experiments the slot parameters were measured, particularly the zone h2, which is characterized by the absence of camber at the θ angle and the formation of the crushed rock stiff core. The established empirical pattern for defining the value of h2 is as follows [11, 19]:
- for incoherent frozen sedimentary rocks (sand)
h2=1,021h-0,45e0,029h; - for coherent frozen sedimentary rocks (loams)
h2=0,728h-0,024e0,067h.
Depending on the h2 value, the slot section is divided into two zones.
In the scheme of forces effect (Fig.2) force N and its components P01 and P02 are the external forces, which act on the rock mass from the working body. The force P and its components P1 and P2 are the internal forces, which act on the separated chip element from the stiff core. The forces P'01 and P'02 are the components of the internal resistance to crushing, which act on the stiff core from the rock mass. The forces Pbpx and Pbpy are the components of the rock mass internal resistance, which act on the working body blunting place. The force P01 is equal the sum of three summands, specifically of the tangential component of the rock mass force effect on the stiff core, the tangential component of the rock mass force effect on the separated chip element, and the tangential component of the rock mass force effect on the working body blunting place. All tangential components of the internal forces effect on the working body are summarized in the formula with definite inclination angles to the x-axis. Thus, the force application in the scheme (Fig.2) is performed for a general idea of the internal resistances during the working body movement in the frozen rock mass, but not for the correspondence to each other.
Omitting the trigonometric ratios of sizes and stresses and summing the resistances in the zones 1 and 2, as well as the resistances associated with the cutting tool blunting, the analytical dependency for determining the tangential component of the frozen sedimentary rock resistance to blocked cutting is obtained:
where b stands for the width of the worn place; δ1 stands for the angle of inclination between the worn place surface and the tangential to the cutting tool movement trajectory; μ stands for the friction angle of the rock on the cutting tool; ξ1 stands for the lateral earth pressure index; φ2 stands for the friction angle of the rock against the rock; αc stands for the cutting angle; θ stands for the front separation angle; ψ stands for the angle between the front surface of the stiff core and the front surface of the cutting tool.
In matters of frozen rock cutting, the stress differentiation in various cross-sectional zones of the chip was not carried out. Therefore, the main difference of the conducted research is the division of the slot section into zones with different stresses. Summing the tangential components of the resistances, which occur in zones of chip elements separation, in the stiff core and in the blunting place, was carried out on the basis of the fundamental laws of solid-state physics, theoretical mechanics and strength of materials.
The degree of rock hardness is taken into account depending (1) on the stresses σf, τ, σcr, the values of which, based on the temperature, are given in technical literature concerning the frozen rock (soil) mechanics. In this case the studies by A.N.Zelenin, G.M.Veselov, A.N.Stepanov, N.K.Pekarskaya, S.S.Vialov, M.I.Rovinsky, G.A.Shloydo, L.I.Sverdlova and many other researchers should be noted.
Deeply blocked cutting (Fig.3) is used for frozen rock destruction less often compared to blocked method [27-29]. During the work of rotary ditch excavators on frozen rocks in the lower part of the face, the rock is cut in thin chips and does not collapse in slots after the cutting tool passage [30, 31]. In this case deeply blocked cutting is observed. A similar process occurs during the work of milling machines on any type of rock of a low or medium hardness [32]. If the ripper tooth of a ripper bulldozer is inserted in the slot again after the passage through the rock using blocked cutting method in order to deepen the slot, deeply blocked cutting occurs [33]. Deeply blocked cutting was investigated using only experimental methods [34, 35], thus, the theoretical interpretation of the issue is of a considerable interest.
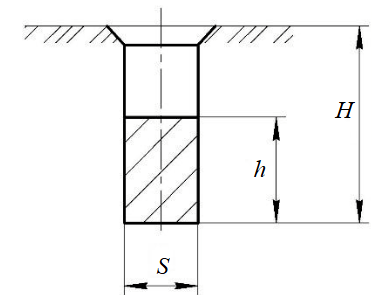
Fig.3. The scheme of slot section during the process of deeply blocked cutting H – distance between the rock mass surface and the slot bottom
The tangential component of the frozen rock resistance to deeply blocked cutting is defined by summing the values of cutting resistance in zones 1 and 2 (Fig.4), taking into account the tangential component of the cut chip shearing resistance along two lateral planes ABCD, as well as along the plane AD and the front surface of the blunted cutting tool from the slot.
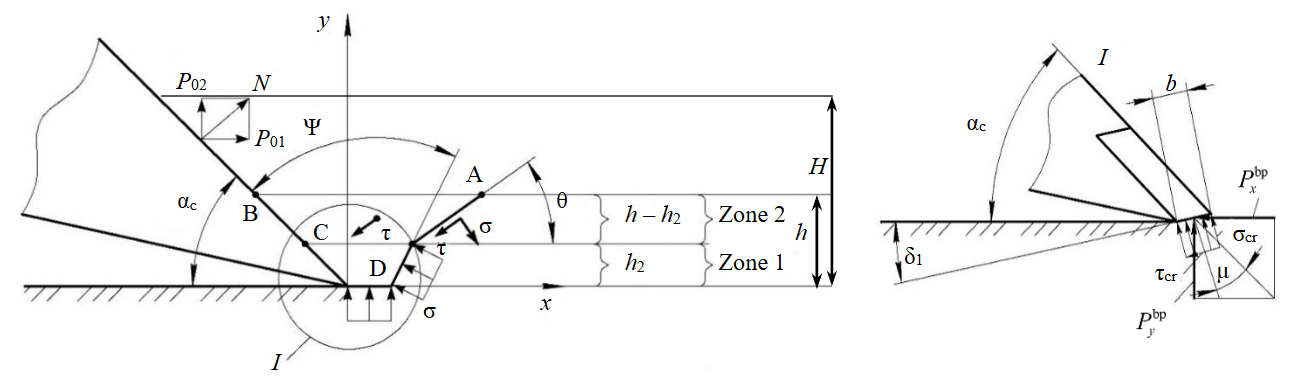
Fig.4. The scheme of emergence of the resistance stresses acting on the separated chip element in limit state during deeply blocked cutting
As a result, the analytical dependency for determining the tangential component of the resistance to deeply blocked cutting is as follows:
where μ1 stands for the rock against steel friction index; γr stands for the gravity body force of the cut rock.
The calculation according to the formula (2) with the parameter values equal to the above stated values shows that the tangential component of cutting resistance is Р01 = 85,600 N, which is 1.6 times more than during blocked cutting.
Cell cutting (Fig.5) is a widely used method for frozen rock excavating machines [36]. They include rotary and chain ditch excavators, ditch-digging attachments on tractors, quarry milling combines, etc. [37, 38].
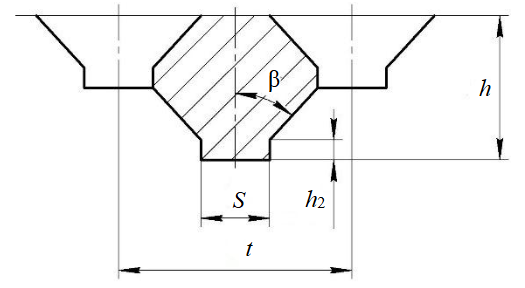
Fig.5. The scheme of slot section during the process of frozen rock cell cutting
t – cutting pitch
In order to analytically determine the tangential component of resistance to cutting Р01, it is advisable to divide the surfaces into four zones (Fig.6) [19], integrate the emerging stresses in each zone and sum the resulting forces, taking trigonometric functions into account.
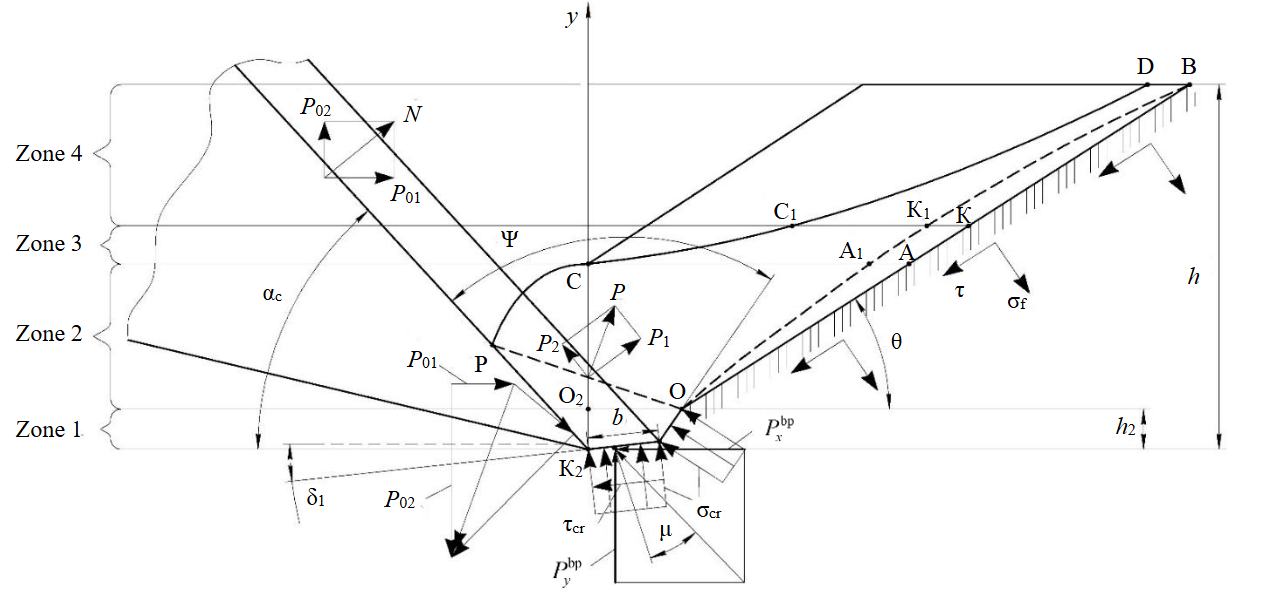
Fig.6. The calculation scheme of cell cutting
As a result, the analytical dependency for determining tangential component of resistance to cell cutting is as follows:
With the before stated quantity values, which are included in the formula (3), the tangential component of cutting resistance to cell cutting is Р01 = 33,400 N, which is 1.63 times less than to blocked cutting and 2.5 times less than to deeply blocked cutting.
The procedure of field and laboratory investigations
In order to confirm the convergence of resulting interrelations (1)-(3) with the physics of frozen sedimentary rock cutting process, a series of experiments on cutting frozen loams and sands with the hardness index 2 in natural environment with the surrounding air temperature from –10 to –15 °C was conducted [39-41]. The cutting process was carried out with the use of multi-purpose cutting stand (Fig.7), geared with a DT-75 tractor. Since finding sand in natural occurrence presents certain difficulties, as it is not to be found anywhere except flood plains, the process of sand cutting was performed in laboratory setting, specifically in a freezing chamber with the temperature from –15 to –20 °C, on frozen blocks with the dimensions of 1.2×1.2×0.4 m. The frozen block was then installed under the cutting tool of the stand.
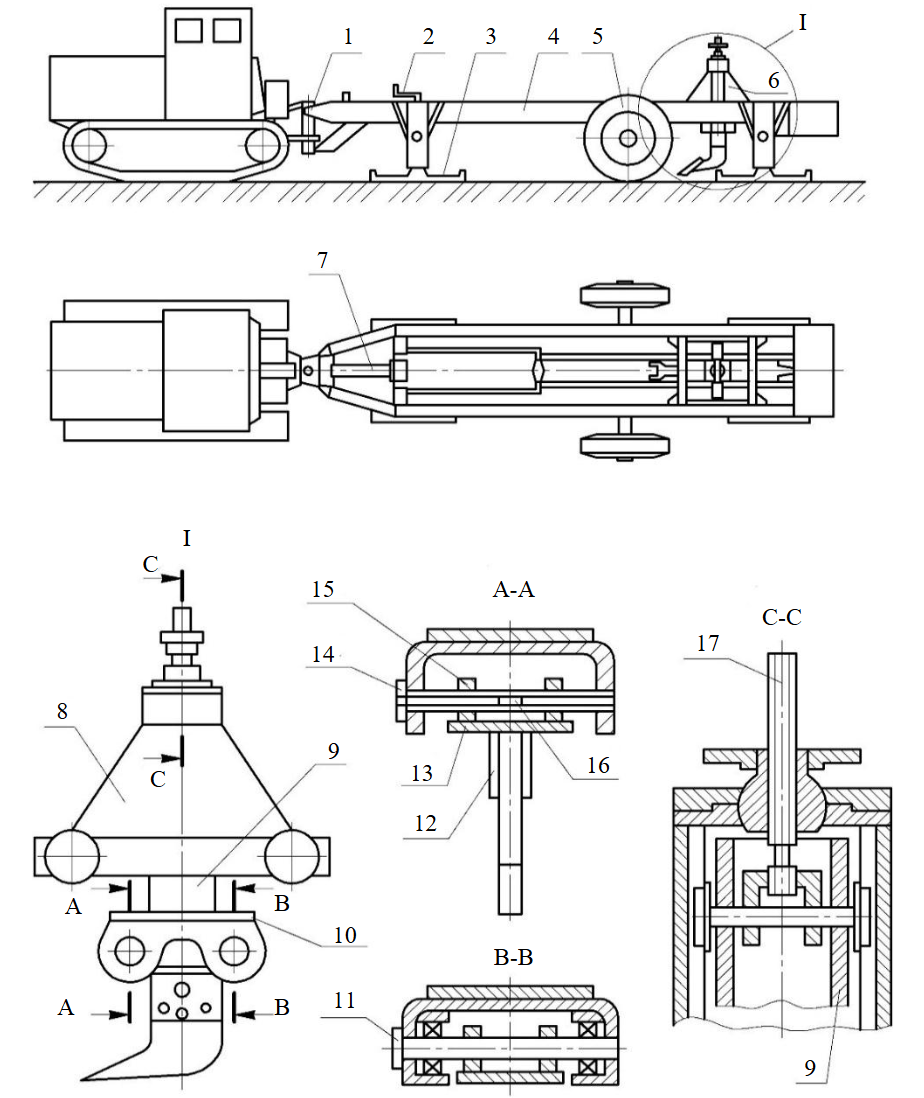
Fig.7. The scheme of the cutting stand for layer-by-layer rock cutting
Steel teeth, which acted as a cutting tool, had the cutting edge width of 40 mm with WC-8 brazed elements and the blunting place of 3 mm. The possibility of teeth penetration into rock was 300 mm.
Cutting stand characteristics are: maximum cutting speed – 0.8 m/s, maximum cutting force – 180 kN, maximum cutting depth – 0.4 m. The stand includes the measuring trolley 6, which is installed on the frame 4 (Fig.7). During the measurement process the horizontal position of the frame is achieved by skids 3, and the tractive force is transmitted from the tractor to the frame through the ball joint 1. The transportation of the stand to the measurement point is performed by means of the pneumatic wheels 5. The distance between the frame and a rock layer is changed with the jackscrews 2, which are built in the skids 3. The measuring trolley 6 movement along the frame 4 guides is performed using the hydraulic cylinder 7, which is connected to the hydraulic system of the tractor. The rack 9, which is installed in the measurement trolley frame 8, is moved using the screw 17. The measuring axis 14 and the rear axis 11 are installed in the holes of flange 10. The working body is suspended on the axes 11, 14 by means of the flanges 13 with the lugs 15 and the guides 12. The tangential component of cutting resistance is measured with the sensors 16, which are installed on the axis 14 vertically. The normal component of cutting resistance is measured with the sensors installed on the axis 14 horizontally.
The rock samples with the height of 100 mm and the diameter of 71.4 mm were used during the compression and tensile shear test by the indirect diametral compression method. The bearing stress was measured by pressing a steel punch with a universal testing machine UMM-50 (GOST 7855-61) in the rock.
During the experimental investigations the following parameters of the slot made by the cutting tool were determined: camber angle β, depth h2 and h, front separation angle θ, the angle between the front surface of the stiff core and the front surface of the cutting tool ψ.
Discussion
As a result of experimental and estimated data comparison using the dependences (1)-(3), a sufficient convergence of the analytical statements with the physics of blocked, deeply blocked and cell methods of frozen sedimentary rock cutting was established (the discrepancy does not exceed 11 %). In this case, several experiments were selected from a large number (Table 1-3).
Table 1
The estimated maximum values of the tangential component of resistance to deeply blocked cutting with one tooth according to equation (2)
| Experiment number | Rock type | h, m | αc, deg | S, mm | b, mm | δ1, deg | μ, deg | h2, mm | ξ1 | φ2, deg | θ, deg | ψ, deg | σсr, N/сm2 | τ, N/сm2 | σf, N/сm2 | Т, °С | Р01, N (estimated) | Р01, N (experimental) | Calculation mistake, % |
| 1 | Frozen sand | 0,1 | 35 | 40 | 5 | 5 | 12 | 20 | 0,4 | 40 | 38 | 80 | 2000 | 300 | 195 | –10 | 5350 | 5280 | 11 |
| 2 | Frozen sand | 0,2 | 35 | 40 | 5 | 5 | 12 | 25 | 0,4 | 40 | 38 | 80 | 2000 | 300 | 195 | –15 | 1070 | 1050 | 10,8 |
| 3 | Frozen loam | 0,1 | 35 | 40 | 5 | 5 | 12 | 23 | 0,4 | 35 | 36 | 75 | 1800 | 250 | 180 | –10 | 19000 | 20000 | –8,15 |
| 4 | Frozen loam | 0,2 | 35 | 40 | 5 | 5 | 12 | 25 | 0,4 | 35 | 36 | 75 | 1800 | 250 | 180 | –10 | 38000 | 37000 | 10,5 |
Table 2
The estimated maximum values of the tangential component of resistance to blocked cutting with one tooth according to equation (1)
| Experiment number | Rock type | h, m | αc, deg | S, mm | b, mm | δ1, deg | μ, deg | h2, mm | φ2, deg | ψ, deg | σсr, N/сm2 | τ, N/сm2 | σf, N/сm2 | Т, °С | Р01, N (estimated) | Р01, N (experimental) | Calculation mistake, % |
| 1 | Frozen sand | 0,1 | 35 | 40 | 5 | 5 | 12 | 20 | 40 | 38 | 2000 | 300 | 195 | –10 | 8480 | 8300 | 9,6 |
| 2 | Frozen sand | 0,2 | 35 | 40 | 5 | 5 | 12 | 25 | 40 | 38 | 2000 | 300 | 195 | –15 | 16000 | 15900 | 9,7 |
| 3 | Frozen loam | 0,1 | 35 | 40 | 5 | 5 | 12 | 23 | 35 | 36 | 1800 | 250 | 180 | –10 | 30400 | 30800 | –9,7 |
| 4 | Frozen loam | 0,2 | 35 | 40 | 5 | 5 | 12 | 25 | 35 | 36 | 1800 | 250 | 180 | –10 | 60800 | 60100 | 9,1 |
Table 3
The estimated maximum values of the tangential component of resistance to cell cutting with one tooth according to equation (3)
| Experiment number | Rock type | t, Т, °С | σf, N/сm2 | μ, deg | t, mm | h, m | S, mm | αc, deg | δ1, deg | θ, deg | h2, mm | τ, N/cm2 | σсr, N/cm2 | Р01, N (estimated) | Р01, N (experimental) | Calculation mistake, % |
| 1 | Frozen sand | –10 | 120 | 12 | 132 | 0,1 | 35 | 45 | 15 | 25 | 11 | 300 | 2000 | 19300 | 18000 | –7,2 |
| 2 | Frozen sand | –10 | 120 | 12 | 300 | 0,2 | 35 | 45 | 15 | 25 | 12 | 300 | 2000 | 20300 | 19000 | –6,9 |
| 3 | Frozen sand | –10 | 120 | 12 | 140 | 0,1 | 35 | 45 | 15 | 25 | 9 | 300 | 2000 | 18000 | 17500 | –2,86 |
| 4 | Frozen loam | –10 | 120 | 12 | 350 | 0,2 | 58 | 45 | 15 | 25 | 13 | 300 | 2000 | 34500 | 32000 | –7,8 |
| 5 | Frozen loam | -8 | 87 | 24 | 230 | 0,2 | 35 | 45 | 15 | 15 | 16 | 250 | 1800 | 6500 | 7000 | 7,1 |
| 6 | Frozen loam | 9 | 87 | 24 | 140 | 0,11 | 22 | 45 | 15 | 15 | 20 | 250 | 1800 | 5550 | 6100 | 9 |
Conclusion
The developed analytical dependences for determining the tangential component of the process of frozen sedimentary rock cutting with a single cutting tool provide a reasonable opportunity to determine the required tractive forces for the excavating machine cutting tools the and power for the drive under given shearing, tensile and bearing limit stresses. Therefore, the actual efficiency and profitability of work is determined. The presented analytical dependences allow obtaining the calculation results with a permissible error compared to data, which results from the experimental investigations. The numerical calculations conducted using the three analytical dependences for determining the tangential component of cutting resistance under equal parameters of the cutting tool, cut chip thickness and width, strength properties of the rock show that the value of resistance to deeply blocked cutting is 1.6 times more than to blocked cutting and 2.5 times more than to cell cutting. Thus, it is preferred to use cell cutting in machines designed for frozen sedimentary rock excavation.
References
- Subbotin Yu.V., Oveshnikov Yu.M., Avdeev P.B. Preparation of frozen rocks for excavation in placer mining in Transbaikal region. Mining Informational and Analytical Bulletin. 2019. N 3, p. 125-133 (in Russian). DOI: 10.25018/0236-1493-2019-03-0-125-133
- Tikhonov V.A., Dudnik G.A., Panfilov S.Yu., Zhulikov V.V. Specific Features of Blasting Operations in Mining Minerals in Northern and Arctic Regions of Russia. Russian Mining Industry. 2021. N 2, p. 102-106 (in Russian). DOI: 10.30686/1609-9192-2021-2-102-106
- Egorov V.V., Volokitin A.N., Ugolnikov N.V., Sokolovsky A.V. Justification of parameters and technology of drilling and blasting operations to ensure the required lumpiness. Russian Mining Industry. 2021. N 3, p. 110-115 (in Russian). DOI: 10.30686/1609-9192-2021-3-110-115
- Kamenev A.V. Analysis of frozen soil loosening. Nauchno-prakticheskie issledovaniya. 2020. N 5-2 (28), p. 114-118.
- Iliukhin A.V., Marsov V.I., Dzhabrailov Kh.A., Chantieva M.E. Features of soil development processes by digging and transporting machines. The Eurasian Scientific Journal. 2018. Vol. 10. N 2. N 65SAVN218 (in Russian).
- Perepelking M.A., Mokritskaya N.I. Revisiting: the development of earthmoving, excavating and transportation machinery implements. Russian Mining Industry. 2019. N 2 (144), p. 81-82 (in Russian). DOI: 10.30686/1609-9192-2019-2-144-81-82
- Tretyak A.Ya., Popov V.V., Grossu A.N., Borisov K.A. Innovative approaches to designing highly efficient rock-breaking tool. Mining Informational and Analytical Bulletin. 2017. N 8, p. 225-230 (in Russian). DOI: 10.25018/0236-1493-2017-8-0-225-230
- Yi Liu, Feng Dai. A review of experimental and theoretical research on the deformation and failure behavior of rocks subjected to cyclic loading. Journal of Rock Mechanics and Geotechnical Engineering. 2021. Vol. 13. Iss. 5, p. 1203-1230. DOI: 10.1016/j.jrmge.2021.03.012
- Pebrianto R., Asof M., Susilo B.K., Gofar N. Evaluation of Factors Affecting Ripping Productivity in Open Pit Mining Excavation. Electronic Journal of Geotechnical Engineering. 2014. Vol. 19. Bund. Z3, p. 10447-10456.
- Ivkin V.S., Volynshchikov P.Yu. Frozen ground excavation under reduced building conditions. Vestnik of Ulyanovsk State Technical University. 2013. N 2 (62), p. 62-66 (in Russian).
- Shemyakin S.A., Gamolya Yu.A., Cheban A.Yu. Technical and technological solutions of the development of frozen and hard rocks in mining and construction. Khabarovsk: Izd-vo DVGUPS, 2017, p. 188.
- Buryy G.G., Poteryaev I.K., Skobelew S.B., Kovalevskiy V.F. Improving the productivity of a single-buckle hydraulic excavator with a bucket of new construction. News of the Tula State University. Technical sciences. 2019. Iss. 9, p. 12-19 (in Russian).
- Zhabin A.B., Polyakov A.V., Averin E.A. et al. Ways of development for the theory of rock and coal destruction by picks. Ugol. 2019. N 9 (1122), p. 24-28 (in Russia). DOI: 10.18796/0041-5790-2019-9-24-28
- Xinzhong Wang, Weiquan Fang, Dianlei Han, Xuegeng Chen. Review of the Research on Soil Disturbance by Tools. Applied Sciences. 2023. Vol. 13. Iss. 1. N 338. DOI: 10.3390/app13010338
- Feng Hou, Yuanming Lai, Enlong Liu et al. A creep constitutive model for frozen soils with different contents of coarse grains. Cold Regions Science and Technology. 2018. Vol. 145, p. 119-126. DOI: 10.1016/j.coldregions.2017.10.013
- Shemyakin S.A., Shishkin E.A. Analytical theories for determining the resistances to frozen rock cutting (loosening) and their application in the practice of earthmoving machines calculation. Khabarovsk: Izd-vo Tikhookeanskogo gosudarstvennogo universiteta, 2014, p. 144.
- Kyznetsova V.N., Savinkin V.V., Ratushnaya T.Y. et al. Study of the Spatial Distribution of Forces and Stresses on Wear Surfaces at Optimization of the Excavating Part of an Earthmoving Machine Transverse Profile. Coatings. 2021. Vol. 11. Iss. 2. N 182. DOI: 10.3390/coatings11020182
- Shemyakin S.A., Cheban A.Yu. Determination of resistance to cutting of frozen rocks deeply blocked (slot). Journal of Mining equipment and electromechanics. 2015. N 6, p. 39-44 (in Russian).
- Shemyakin S.A. Justification of surface mining effective technologies based on the improvement of rock excavation process: Avtoref. dis. ... d-ra tekhn. nauk. Khabarovsk: Institut gornogo dela DVO RAN, 2004, p. 34.
- Aresh B., Khan F.N., Haider J. Experimental investigation and numerical simulation of chip formation mechanisms in cutting rock-like materials. Journal of Petroleum Science and Engineering. 2022. Vol. 209. N 109869. DOI: 10.1016/j.petrol.2021.109869
- Kuznetsova V.N. Physical modeling of the contact process interactions of the working body of the digging machine with frozen soil. Tomsk State University Journal of Mathematics and Mechanics. 2019. N 61, p. 70-81 (in Russian). DOI: 10.17223/19988621/61/7
- Xuezhen Wang, Sen Zhang, Hongbo Pan et al. Effect of soil particle size on soil-subsoiler interactions using the discrete element method simulations. Biosystems Engineering. 2019. Vol. 182, p. 138-150. DOI: 10.1016/j.biosystemseng.2019.04.005
- Zhelykevich R.B., Selivanov N.I., Kaiser Yu.F., Lysyannikov A.V. Determination of stresses caused in the disc cutter, blocked cutting of frozen soils. News of the Tula State University. Technical sciences. 2015. Iss. 8. Part 2, p. 66-78 (in Russian).
- Kuznetsova V.N., Kuznetsov I.S. Simulation of the contact process interactions of land-moving and earth-transport machines’ working bodies with frozen soil. The Russian Automobile and Highway Industry Journal. 2018. Vol. 15. N 2 (60), p. 189-198 (in Russian). DOI: 10.26518/2071-7296-2018-2-189-198
- Hu M., Gao T., Dong X et al. Simulation of soil-tool interaction using smoothed particle hydrodynamics (SPH). Soil and Tillage Research. 2023. Vol. 229. N 105671. DOI: 10.1016/j.still.2023.105671
- Tekeste M.Z., Way T.R., Syed Z., Schafer R.L. Modeling soil-bulldozer blade interaction using the discrete element method (DEM). Journal of Terramechanics. 2020. Vol. 88, p. 41-52. DOI: 10.1016/j.jterra.2019.12.003
- Troyanovskaya I.P., Raznoshinskaya A.V., Kozminykh V.A., Leshchenko E.A. Experimental tests of industrial-scale ripping of soil. Gornyi zhurnal. 2021. N 5, p. 87-90 (in Russian). DOI: 10.17580/gzh.2021.05.11
- Rashidov T., Djuraeva N., Atamirzayev M., Normuminov B. Strain state agrogenic soil under its interaction with a deep ripper. IOP Conference Series: Materials Science and Engineering. 2020. Vol. 896. N 012109. DOI: 10.1088/1757-899X/896/1/012109
- Ucgul M., Saunders C., Fielke J.M. Comparison of the discrete element and finite element methods to model the interaction of soil and tool cutting edge. Biosystems Engineering. 2018. Vol. 169, p. 199-208. DOI: 10.1016/j.biosystemseng.2018.03.003
- Shemyakin S.A., Shishkin E.A. Physical and mathematical model of rock destruction by a milling machine cutter. Journal of Mining Institute. 2021. Vol. 251, p. 639-647. DOI: 10.31897/PMI.2021.5.3
- Yadav S., Saldana C., Murthy T.G. Experimental investigations on deformation of soft rock during cutting. International Journal of Rock Mechanics and Mining Sciences. 2018. Vol. 105, p. 123-132. DOI: 10.1016/j.ijrmms.2018.03.003
- Nikolayev V.A. Calculation of energy consumption for soil cutting horizontal blade by the analysis process. Scientific and Technical Journal of Bryansk State University. 2019. N 2, p. 243-250 (in Russian). DOI: 10.22281/2413-9920-2019-05-02-243-250
- Katinas E., Chotěborský R., Linda M., Jankauskas V. Wear modelling of soil ripper tine in sand and sandy clay by discrete element method. Biosystems Engineering. 2019. Vol. 188, p. 305-319. DOI: 10.1016/j.biosystemseng.2019.10.022
- Makange N.R., Changying Ji, Nyalala I. et al. Prediction of precise subsoiling based on analytical method, discrete element simulation and experimental data from soil bin. Scientific Reports. 2021. Vol. 11. N 11082. DOI: 10.1038/s41598-021-90682-w
- Cviklovič V., Mojžiš M., Majdan R. et al. Data Acquisition System for On-the-Go Soil Resistance Force Sensor Using Soil Cutting Blades. Sensors. 2022. Vol. 22. Iss. 14. N 5301. DOI: 10.3390/s22145301
- Boyarkina I.V. The specific energy consumption for processes of soil digging by digging machine bucket. Omsk Scientific Bulletin. 2017. N 2 (152), p. 5-7 (in Russian).
- Hegde A., Murthy T.G. Experimental studies on deformation of granular materials during orthogonal cutting. Granular Matter. 2022. Vol. 24. Iss. 3. N 70. DOI: 10.1007/s10035-022-01227-5
- Hegde A., Murthy T. An experimental study on shear bands in sand using the orthogonal cutting setup. EPJ Web of Conferences. 2021. Vol. 249. N 10007. DOI: 10.1051/epjconf/202124910007
- Aresh B., Khan F.N., Haider J. Experimental investigation and numerical simulation of chip formation mechanisms in cutting rock-like materials. Journal of Petroleum Science and Engineering. 2022. Vol. 209. N 109869. DOI: 10.1016/j.petrol.2021.109869
- Zaied M.B., El Naim A.M., Abdalla O.A., Sulieman A.M. Effect of Tine Depth and Width on Soil Failure Angle, Cutting Coefficients and Power in Three-Dimensional Case: Computer Modeling. World Journal of Agricultural Research. 2016. Vol. 4. N 1, p. 24-30. DOI: 10.12691/wjar-4-1-4
- Masch F.R., Hecker R.L., Flores G.M. et al. On-the-go sensor with embedded load cells for measuring soil mechanical resistance. Ciencia del Suelo. 2020. Vol. 38. N 1, p. 21-28.
