Комплексная оценка деформирования системы жесткой армировки при конвергенции крепи шахтного ствола в неустойчивых породах
- 1 — канд. техн. наук заведующий лабораторией АО «ВНИИ Галургии» ▪ Orcid
- 2 — д-р техн. наук главный научный сотрудник АО «ВНИИ Галургии» ▪ Orcid
- 3 — ведущий инженер АО «ВНИИ Галургии» ▪ Orcid
Аннотация
Эксплуатация вертикальных шахтных стволов в сложных горно-геологических условиях связана с рядом особенностей. Одна из них – радиальные перемещения бетонной крепи ствола, обусловленные влиянием горного давления на напряженно-деформированное состояние горной выработки. Система жесткой армировки, расстрелы которой закреплены в бетонной крепи, испытывает при этом упругопластические деформации, их величина увеличивается с течением времени. Это приводит к отклонению проводников от проектных параметров, ослаблению болтовых соединений, ухудшению динамических свойств геотехнической системы «подъемный сосуд – армировка», увеличению скорости износа элементов системы армировки, повышению рисков создания аварийной ситуации. Предложена комплексная оценка перемещений характерных точек системы расстрелов, основанная на приближенных инженерных соотношениях, численном моделировании процесса деформирования системы расстрелов и лазерных измерениях конвергенции внутренней поверхности бетонной крепи ствола. Методика апробирована на примере системы армировки скипо-клетевого ствола калийного рудника, перемещение характерных точек которой определяется величиной радиальных смещений поверхности бетонной крепи ствола. Их оценка произведена с использованием мониторинговых измерений и данных профилировки. Полученные результаты дают возможность обосновать необходимость и сроки проведения ремонтных работ. Показано, что ухудшение состояния системы армировки на различных ярусах происходит с разной скоростью, определяемой в том числе механическими характеристиками слоев породного массива, расположенного на данной глубине.
Введение
Вертикальные шахтные стволы относят к выработкам первого класса ответственности, так как нарушение их нормальной эксплуатации способно привести к остановке работы всего горно-добывающего предприятия (СП 91.13330.2012). Главным показателем надежной и безаварийной работы шахтного ствола является работоспособность его армировки, состоящая из системы конструкций, обеспечивающих движение подъемных сосудов при заданных режимах работы подъемной установки в течение всего срока эксплуатации ствола [1]. Расчет жесткой армировки выполняется по условиям динамической устойчивости движения подъемных сосудов в проводниках и производится на стадии проектирования шахтных стволов. Кроме того, входящие в армировку элементы рассчитываются на соответствие жесткостным и прочностным характеристикам [1-3]. Остальные нагрузки считаются несущественными, поэтому ими пренебрегают при расчете или учитывают некоторые коэффициенты запаса при определении нагрузок от подъемных сосудов [4]. Упрощение расчетной схемы может привести к неточному определению параметров жесткой армировки стволов калийных рудников, поэтому необходимо учитывать сложное, изменяющееся во времени взаимодействие геотехнической системы «жесткая армировка – крепь ствола» [4].
Из натурных наблюдений известно [5], что в течение эксплуатации шахтных стволов калийных рудников неизбежно происходит коррозионный и механический износ расстрелов и направляющих проводников. Износ элементов армировки приводит к изменению их геометрических характеристик – уменьшению толщины стенок проводников и расстрелов и снижению жесткости всей системы армировки. Если ствол находится в сложных горно-геологических условиях (малоустойчивый породный массив, пригрузка от прохождения дополнительных выработок и т.п.), то возникают деформации некоторых участков крепи и, как следствие, армировки. Деформации в монолите бетона могут достигать такой величины, что в определенный момент возникает ситуация, при которой невозможен свободный проход подъемного сосуда в колее проводников. Это приводит к ухудшению динамических свойств системы «подъемный сосуд – армировка» и снижению эксплуатационных характеристик [5, 6]. Для устранения нарушения выполняют работы по замене деформированного участка расстрела на прямолинейный, предварительно освободив его путем выдавливания заделки конца расстрела из бетонной крепи [6]. Каждая точка заделки расстрела раскрывается до размеров, необходимых для приведения колеи проводников в базовое, проектное положение. При необходимости убирается не только бетонная крепь, но и зачищается соляная порода на достаточную длину и ширину. Подробное описание условий работы жесткой армировки стволов с перечислением основных типов нагрузок и действия их на армировку представлено в работах [7-9].
Постановка проблемы
Исследованиями различных авторов установлено, что при эксплуатации шахтного ствола в сложных горно-геологических условиях наблюдается деформация бетонной крепи в результате изменения вмещающих ствол массива пород [10-12]. Деформация бетонной крепи передается на жесткую армировку, в результате чего происходит нарушение и проектное изменение расстрелов и проводников [13-15]. Различные аспекты влияния подработанного пространства на геометрию ствола и эксплуатационные характеристики обсуждаются в работах [16, 17].
Во время непрерывной эксплуатации крепи и системы армировки шахтных стволов накапливаются и появляются следующие проблемы [18-20]:
- изменение геометрии колеи направляющих проводников, что может привести к выходу из колеи или заклиниванию подъемных сосудов. Это грозит возникновением аварийной ситуации с тяжелыми последствиями;
- в связи с интенсивным истиранием проводников и расстрелов, накоплением усталостных напряжений и коррозионного износа уменьшается время службы элементов армировки;
- стоимость эксплуатации стволов, связанная с большими временными затратами регулярных осмотров и трудоемкостью ремонтов узлов крепления армировки, увеличивается.
Для решения этих проблем необходимо выполнить комплексную оценку технического состояния всех элементов жесткой армировки как единой рамной конструкции с учетом конвергенции бетонной крепи.
Таким образом, задача исследования – изучение особенностей совместного деформирования геотехнической системы «жесткая армировка – крепь ствола» с последующей оценкой определения критических деформаций и их влияния на выбор конструктивных и технологических решений по армированию вертикальных стволов.
Методы
Для решения поставленной задачи применялся как инженерный подход, так и численный – метод конечных элементов (МКЭ) с использованием пакета прикладных программ ANSYS. Необходимо определить зависимости между величиной конвергенции бетонной крепи и величиной деформации (перемещений) жесткой армировки на примере скипо-клетевого шахтного ствола калийного рудника. На практике широко применяются инструментальные методы исследования и контроля систем армировки и подъемных сосудов с использованием современных средств измерений [21-23] и мониторинга [24]. В качестве расчетных методов прежде всего применяется инженерный [25-27], основанный на приближенных подходах теоретической механики и сопротивления материалов [28, 29]. Развиваются также подходы, построенные на численном решении подобных задач методом конечных элементов [30-32]. Некоторые из них рассматривают коробчатые металлоконструкции с учетом коррозии [33-35]. Отметим, что методами численного моделирования рассматриваются пока только отдельные элементы систем армировки, хотя, как представляется авторам, этот метод в сочетании с инструментальными методами мониторинга имеет значительные перспективы.
Предложен комплексный подход к изучению совместного деформирования геотехнической системы «жесткая армировка – крепь ствола», включающий инженерный и численный методы, а также инструментальные измерения деформации крепи. Представлены приближенные соотношения и разработана численная 3D-модель для оценки деформаций системы жесткой армировки с учетом конвергенции бетонной крепи ствола. На примере скипо-клетевого ствола калийного рудника определены напряженно-деформированное состояние и перемещения системы армировки, представлена прогнозная оценка работоспособности армировки при постоянном действии фактора конвергенции бетонной крепи, расположенной в соляных породах.
Инженерная постановка задачи
Основная задача для инженерной оценки работоспособности армировки при действии фактора конвергенции внутреннего диаметра бетонной крепи – анализ перемещений характерных точек для сложной системы расстрелов с течением времени. Сформулировать уравнения для аналитического определения перемещений характерных точек для сложной системы расстрелов с учетом всех сопряжений и точек крепления невозможно. Ограничимся здесь приближенными (инженерными) оценками перемещений в рамках, сделанных ниже допущений. Все точки крепления ярусов армировки в бетонной крепи перемещаются в радиальном направлении на величину ΔR, определяемую конвергенцией крепи при ползучести соляных пород под действием горного давления и зависящую от времени.
Введем систему координат ОХY с началом координат, расположенным в центре ствола (рис.1). Здесь буквами A, B, …, I, J обозначены точки крепления расстрелов ствола Р1-Р8 к бетонной крепи, а буквой B1 новое положение точки B при радиальной конвергенции крепи ствола. Исходя из геометрических размеров системы расстрелов, для каждой точки крепления можно определить угол между радиальным направлением (отрезком, связывающим центр ствола и данную точку, показанным пунктиром) и осью OX. На рис.1 в качестве примера показан угол jВ для точки крепления В. Через эти углы для каждой точки крепления можно найти перемещения соответствующей точки вдоль осей координат, например
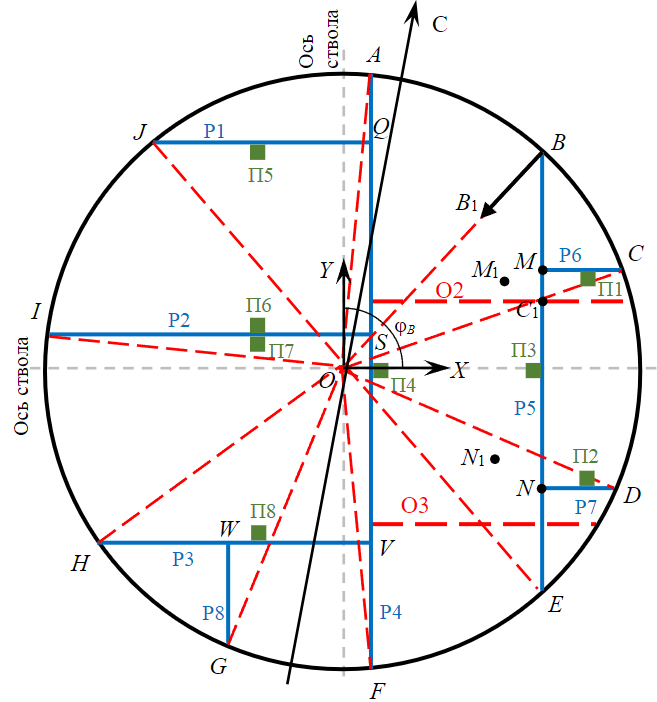
Рис.1. Схема расстрелов и проводников (на примере скипо-клетевого ствола)
Исходя из перемещений всех точек крепления армировки, необходимо оценить новые положения узлов сопряжений продольных и поперечных расстрелов (точки M, N, Q, S, V, W). В общем случае это сложная нелинейная задача, в которой необходимо учитывать как изменение углов в точках крепления и сопряжения расстрелов, так и их возможный изгиб в горизонтальной плоскости из-за потери устойчивости. В случае изгиба центральная часть пролета расстрела получает дополнительное перемещение. Учет всех этих факторов при получении инженерных оценок требует использования дополнительных предположений.
Рассмотрим в качестве примера расстрел Р5, имеющий сопряжения с расстрелом Р6 в точке M и расстрелом Р7 в точке N (рис.1), с возможностью изгиба, приводящего к максимальному перемещению вдоль оси Х середины расстрела в месте соединения с проводником П3.
Точка М при конвергенции крепи ствола перейдет в точку М1, а точки крепления B и C в точки B1 и C1. Мы предполагаем, что отрезки расстрелов сохраняют свою длину BM = B1M1 и CM = C1M1 (при этом угол сопряжения BMC может измениться). Поэтому координаты новых точек крепления
Примем, что
Нужно отметить, что на положение точки M1 будут влиять и другие перемещения точек D, E, а также точки сопряжения расстрелов Р5 и Р7. Кроме того, большие пролеты расстрелов между точками крепления и/или точками сопряжений могут изгибаться в горизонтальной плоскости.
Оценим стрелу прогиба расстрела Р5 на участке М1N1, полагая, что происходит потеря устойчивости расстрела при его сжатии в направлении вдоль его оси. Как известно, при достижении критической силы сжатия балка теряет устойчивость и принимает новую (в частном случае плоскую) синусоидальную форму [36]. Количество (или их доля) волн синусоиды зависит от граничных условий закрепления балки. В нашем случае сжимающие силы не действуют строго соосно, поскольку для рассматриваемых случаев расстрелы вмонтированы в бетонную крепь, которая с течением времени деформируется радиально, создавая две проекции перемещений торцов расстрела: вдоль и поперек его оси.
Следуя статье [36], полагаем, что кривая изгиба защемленной балки при потере устойчивости представляет собой полуволну синусоиды, изображенной на рис.2, где показана половина изогнутой кривой балки, пунктиром изображено ее начальное положение.
Первоначальная длина расстрела L, он изгибается со стрелой прогиба С, которую и нужно оценить после смещения одного торца балки вдоль ее оси относительно другого (закрепленного) на величину Δ. Условием для определения стрелы прогиба C является равенство исходной длины половины расстрела L/2 и его длины S в изогнутом состоянии. Как известно, длина кривой определяется интегралом [37]
где a – длина участка интегрирования; у′– производная по x.
В нашем случае y = 0,5Csin(πx/a); a = 0,5(L – Δ). Вводя новую переменную m = –(0,5Cπ/a)2, сведем соотношение (1) к полному нормальному эллиптическому интегралу Лежандра 2-го рода E2(m), не имеющему выражение в квадратурах,
При малых m (стрела прогиба значительно меньше длины расстрела) функция Е2(m) разлагается в виде быстросходящегося степенного ряда
где О(m3) – величина (остаток степенного ряда), порядок которой не превосходит m3.
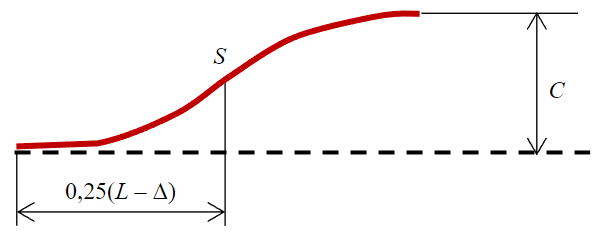
Рис.2. Схема изгиба балки-расстрела
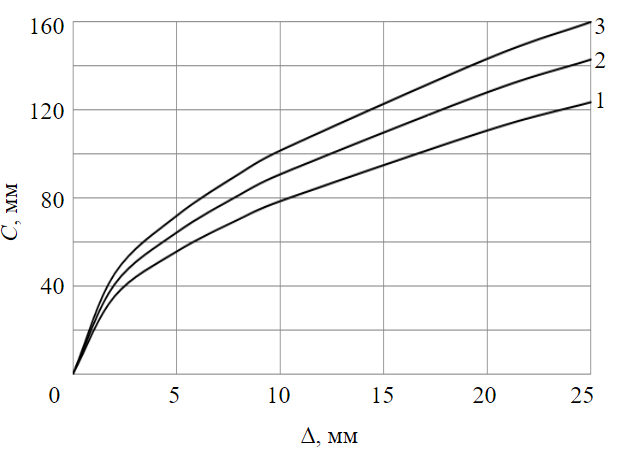
Рис.3. Зависимость стрелы прогиба от величины Δ для различной длины расстрела 1 – 1,5 мм; 2 – 2,0; 3 – 2,5
В данном случае m ≤ 0,1, следовательно достаточно использовать в разложении (7) два члена ряда, чтобы получить разумное инженерное приближение.
Таким образом, с учетом требования равенства длин кривых балки-расстрела до и после деформации, выражений для a, m и разложения (7) получим
Соотношение (8) позволяет получить аналитическое выражение для стрелы прогиба
На рис.3 показана сильная нелинейность зависимости от величины смещения торца расстрела вдоль его оси Δ, особенно при малых значениях Δ: так при Δ = 5 мм стрела прогиба C = 55-72 мм в представленном диапазоне L. Полученные зависимости рассмотрим при анализе системы расстрелов на примере скипо-клетевого ствола.
Оценка перемещений характерных точек расстрелов
С точки зрения безаварийной эксплуатации армировки и подъемных сосудов прежде всего важно оценить величину перемещений точек расстрелов в направлениях, перпендикулярных расстрелу, в местах крепления проводников, поскольку они могут привести как к заклиниванию подъемного сосуда, так и к его выходу из колеи направляющих проводников. Интересующие нас перемещения можно выразить через соответствующие смещения узлов крепления расстрелов и величину ΔR аналогично формуле (1):
где C(SV), C(MN) – стрелы прогиба пролетов расстрелов SV и MN, определяемые с помощью графических зависимостей.
Учитывая зависимости перемещения узлов крепления расстрелов от величины ΔR аналогично формуле (1), соотношения (10) приведем к виду:
Формулы (11) представляют собой конечный результат приближенного подхода для оценки перемещений точек расстрелов в местах крепления проводников. Эти формулы справедливы для системы расстрелов (см. рис.1).
Таким образом, максимальные перемещения реализуются на проводнике П4, далее на проводниках П3, П5 и П8. Следовательно, с течением времени проблемы будут возникать прежде всего для этих проводников. Именно они и должны быть предметом пристального внимания при периодическом осмотре состояния армировки ствола.
Численное 3D-моделирование
Достаточно перспективный метод математического моделирования позволяет рассмотреть систему армировки как единую рамную конструкцию в комплексе с бетонной крепью. Применение численных методов учитывает изменение множества различных факторов геометрического и физического состояния армировки, таких как коррозионное уменьшение толщины стенок профиля, механические характеристики применяемой стали (модуль упругости, предел текучести, предел прочности) [33-35, 38], напряжение в системе «армировка – крепь ствола» и др.
Геометрическая модель и фрагмент модели с сеткой КЭ показаны на рис.4. Граничные условия для рассматриваемой геометрической модели армировки состоят в задании проекций перемещений по осям системы координат ОХY для всех точек крепления (торцевых сечений) расстрелов ствола Р1-Р8 к бетонной крепи аналогично тому, как это было сделано в инженерном подходе (1). На практике расстрелы заходят в бетонную крепь и закрепляются в ней путем создания дополнительных прокладок (клиньев), а также последующего бетонирования созданной под расстрел «лунки». Такое крепление не может обеспечить «идеальную заделку», в ходе эксплуатации бетон в лунке может растрескаться, а клинья ослабнуть. Все это может привести к созданию вместо «идеальной заделки» упругой шарнирной опоры, а также «проскальзыванию» расстрела при больших осевых нагрузках внутрь бетонной крепи.
Для моделирования этих факторов на торцах расстрела формировались «фиктивные» объемы (рис.4, а), длиной не менее 30 см (на такую величину расстрелы заходят в бетон), на торцах которых и задавались проекции перемещений. Упругий шарнир моделировался заданием пониженных (в 2 раза) по сравнению с самим расстрелом упругих свойств «фиктивных» объемов. Принятая расчетная схема моделирует понижение жесткости бетона в «лунке» крепления расстрела и его частичное «проскальзывание» в сторону породного массива. Таким образом, разработанная численная модель может привести к большим расчетным изгибным перемещениям расстрелов, чем в реальности, т.е. к некоторому «запасу» при прогнозе опасного состояния системы армировки.
Классическая математическая постановка задачи оценки напряженно-деформированного состояния упругопластического тела [39, 40] включает: уравнения равновесия, граничные условия в перемещениях и напряжениях, уравнения Коши, уравнения линейной упругости изотропного тела и уравнения пластичности. В настоящей расчетной схеме не учитываются объемные силы, поверхностные нагрузки отсутствуют. Граничные условия представлены наличием заданных перемещений на торцах расстрелов, их пример приведен в соотношении (1).
Материал армировки – сталь 09г2с, предел текучести 325 МПа, предел прочности 470 МПа. Поперечное сечение расстрелов представляет собой замкнутый прямоугольный короб размерами 130×212 мм с толщиной стенки 12 мм.
Задачи решались методом конечных элементов в пакете ANSYS [41] в пространственной постановке. Использованы опции Rate Independent, Isotropic Hardening Plasticity, Mises Plasticity, Multilinear для расчетов пластичности.
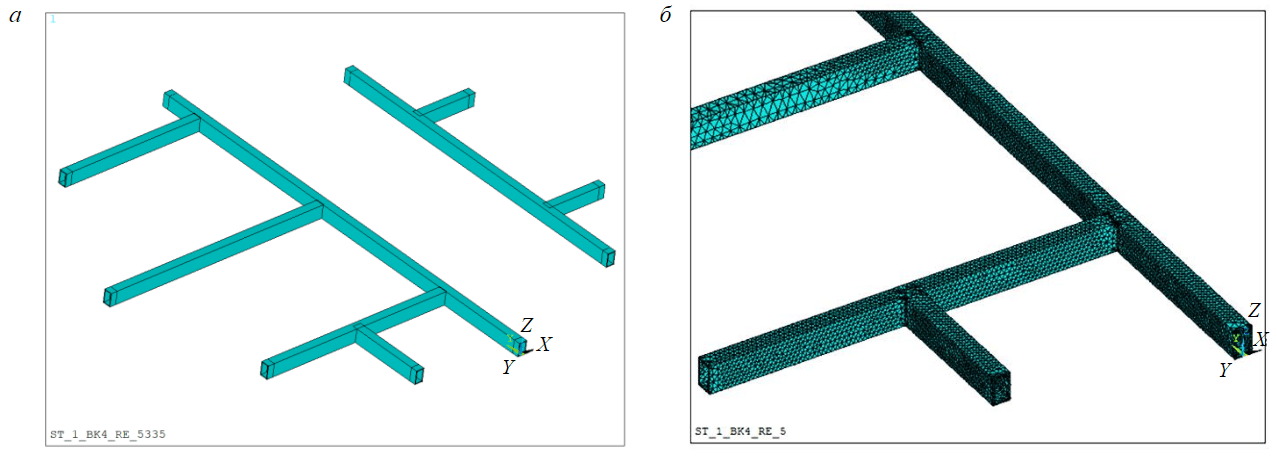
Рис.4. Геометрическая модель системы расстрелов с коробчатым профилем (а) и фрагмент модели с сеткой КЭ (б)
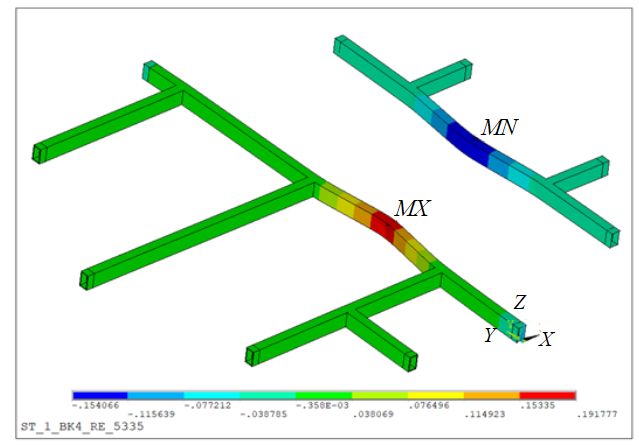
Рис.5. Поле перемещений UХ при ΔR = 30 мм (синий цвет соответствует величине +154 мм, красный +192 мм)
Анализ численных результатов
Проведена серия расчетов деформации армировки при различных величинах конвергенции крепи ствола ΔR. Поле перемещений UХ при величине радиального смещения крепи ΔR = 30 мм представлено на рис.5, где наблюдаются значительные перемещения продольных областей расстрелов Р4 и Р5, расположенных между поперечными расстрелами. Направление осей Х на рис.5 и рис.1 совпадают. Величина перемещений UХ достигает 192 мм (расстрел Р4) и –260 мм (расстрел Р5), что значительно превышает величину конвергенции диаметра крепи ствола 2ΔR= 100 мм. Этот нелинейный эффект связан с сильным изгибом частей продольных расстрелов.
Известно, что подобные деформации армировки приводят к нарушению безопасной эксплуатации ствола значительно раньше, т.е. при меньших величинах конвергенции крепи. Кроме того, упругопластические деформации (и соответствующий уровень напряжений) могут привести к разрушению сварного коробчатого корпуса балок расстрелов. В областях с развитыми пластическими деформациями может возникнуть так называемый пластический шарнир. На практике больше интересуют перемещения характерных точек армировки (например, в местах расположения проводников) в зависимости от величины радиального смещения крепи ΔR.
На рис.6, а показана зависимость перемещения UХ от ΔR для точек крепления проводников П3 и П4. Круглыми маркерами обозначены значения перемещений, вычисленные по инженерным формулам (11), которые дают завышенные по абсолютной величине перемещения по сравнению со значениями, полученными МКЭ. Это объясняется тем, что в численном решении учитывается влияние всей системы расстрелов, а также возможность появления пластических деформаций. Сумма абсолютных величин этих перемещений дает величину уменьшения расстояния между проводниками П3 и П4. Очевидно, что уже при смещении крепи ΔR более 15-20 мм перемещения проводников П3 и П4 становятся неприемлемыми.
На рис.6, б показаны зависимости уменьшения расстояния вдоль оси ОY между проводниками П5 и П6 (кривая 1), П6 и П8 (2), П1 и П2 (3). Максимальные изменения расстояний здесь наблюдаются для проводников П1 и П2. В целом эти величины менее значительные, чем перемещения вдоль оси ОX. Это означает, что максимальные перемещения точек расстрелов, определяющие безаварийное функционирование армировки, возникают в горизонтальной плоскости перпендикулярно направлению главных расстрелов (перемещения в точках крепления проводников П3 и П4). Была проведена аналогичная серия расчетов для армировки, подверженной коррозии, когда стенка коробчатого профиля уменьшалась на 2,4 мм (до 9,6 мм). Уменьшение стенки приводит к увеличению деформаций системы расстрелов, причем возможны качественные изменения характера деформирования главного продольного расстрела. На рис.6, б пунктирной линией обозначена зависимость уменьшения расстояния вдоль оси ОY между проводниками П6 и П8 при толщине коробчатого профиля 9,6 мм.
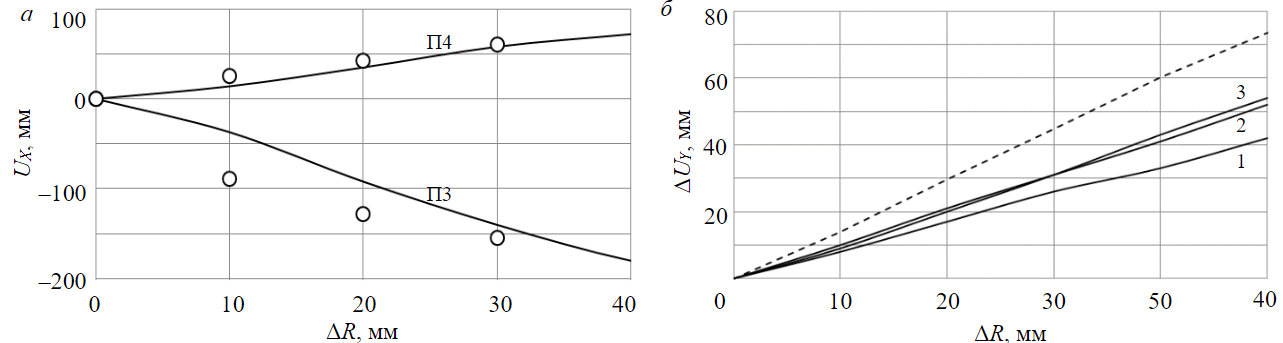
Рис.6. Перемещения характерных точек системы расстрелов
Обсуждение результатов
Анализ и сопоставление результатов моделирования, инженерных расчетов и натурных наблюдений проведены по данным многолетних исследований по изменениям расстояний между параллельными расстрелами Р4 и Р5, выполненных в интервале ярусов № 95-140 скипо-клетевого ствола Березниковского рудника. Расстояние между двумя расстрелами измерялось вдоль жирных красных пунктирных линий, построенных через точки отвесов O2 и O3 (см. рис.1).
Величина ∆R принята по данным лазерного сканирования ствола [8], проведенного в 2021 г., причем для каждого яруса выбиралось одно направление запад – восток. Получена оценка средней скорости изменения диаметра при пересечении со слоями карналлита на участке стационарного изменения диаметра 2,0 мм/год. Так как профилировка проводилась в 2013 г., то за 8 лет среднее изменение диаметра могло составить около 16 мм. Эта величина вычиталась из данных лазерного сканирования. После проведения профилировки до конца 2013 г. была выполнена рихтовка проводников. Результаты были учтены при сравнении расчетных и экспериментальных данных.
На рис.7 представлены зависимости расчетных и экспериментальных измерений уменьшения расстояния между расстрелами за 2013 г. Максимальное расхождение между расчетными и экспериментальными данными с учетом рихтовки – 30 %, среднее расхождение – 10,4 %. Следует отметить качественное совпадение данных расчета по предложенной комплексной методике и профилировочных замеров. Ремонт и замена армировки – процесс крайне трудоемкий, что обуславливает высокие финансовые издержки, связанные с остановкой ствола и соответствующим снижением производительности части или всего калийного рудника. В первые годы эксплуатации армировки шахтного ствола, расположенного в соляном массиве, обходятся локальными ремонтными работами (рихтовкой) по исправлению искривления проводников. Под рихтовкой армировки подразумевается регулирование двух узлов соединения армировки (фланцевых соединений), со смещением продольной оси в каждом узле расстрела на определенную длину, позволяющую вывести колею проводников до базовой величины. В каждом конкретном случае время рихтовки зависит от глубины расположения яруса Н и геомеханических характеристик породного массива на этой глубине.
Например, механические свойства карналлитовых пород значительно уступают сильвиниту или каменной соли, поэтому достижение времени Т раньше может произойти в сильвинито-карналлитовой зоне, а не в зоне подстилающей каменной соли, расположенной значительно глубже. Кроме того, ослабленной зоной является также область сопряжения ствола с горизонтальными выработками. Оценка времени Т в такой области затруднительна, поскольку зависит (помимо вышеуказанных факторов) еще и от геометрии (конструктивных особенностей) области сопряжения ствола с горизонтальными выработками [10].
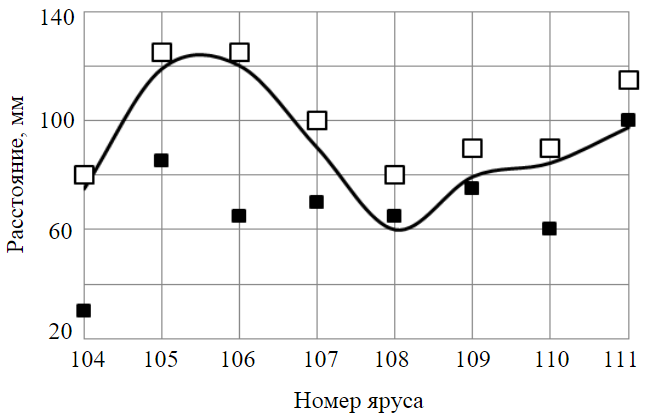
Рис.7. Изменение расстояния между расстрелами: расчетные (сплошная линия) и экспериментальные (квадраты) измерения. Средние значения данных профилировки вдоль линий O2 и O3 без учета рихтовки (черные квадраты); с учетом проведенной в 2013 г. рихтовки (белые квадраты)
Исходя из характерных скоростей изменения диаметра ствола, полученных с помощью лазерного сканирования [8], результатов данных исследований и численного моделирования процесса деформирования бетонной крепи в результате ползучести соляного массива [10], можно сделать следующие выводы:
- для ярусов армировки, расположенных в карналлитовых породах с большими скоростями изменения диаметра ствола, первую рихтовку необходимо производить уже через Т= 4-5 лет после начала эксплуатации, вторую – через 20 лет (примерно 15 лет после первой), третью – через 50 лет (примерно 30 лет после второй);
- первая рихтовка для ярусов с минимальными скоростями изменения диаметра (пересечение с каменной солью, сильвинитом) необходима после Т = 20-25 лет;
- рихтовка на остальных ярусах необходима во временном диапазоне между этими двумя крайними случаями.
Предложенный комплексный подход для каждой системы расстрелов конкретного ствола необходимо выполнять заново: осуществлять лазерный мониторинг, профилировку, формировать новую расчетную схему и проводить численные исследования. Конечно, погрешность прогнозных расчетов может быть различной для разных стволов. Наиболее сложным моментом является применение предлагаемой методики к оценке деформаций расстрелов после проведенной рихтовки – это требует дополнительных исследований.
Таким образом, практическое применение результатов расчетов и выполненных исследований заключается в прогнозе наступления критических деформаций системы жесткой армировки с дальнейшим обоснованием проведения ремонтных работ.
Заключение
Рассмотрены особенности и проблемы эксплуатации жесткой армировки в шахтных стволах калийных рудников, когда бетонная крепь подвергается значительным деформациям при взаимодействии с породным массивом. Предложена комплексная оценка перемещений характерных точек системы расстрелов, основанная на приближенных инженерных соотношениях, численном моделировании процесса деформирования системы расстрелов и лазерных измерениях конвергенции внутренней поверхности бетонной крепи ствола.
Проведено численное моделирование полной системы расстрелов жесткой армировки в 3D-постановке при конвергенции бетонной крепи ствола, выявлены особенности деформирования расстрелов, максимальные смещения характерных точек. Выполнено сравнение инженерных и численных оценок перемещений системы расстрелов на различных ярусах с данными мониторинга (профилировки) и с лазерными измерениями внутренней поверхности бетонной крепи скипо-клетевого ствола калийного рудника. Исходя из оценок скоростей конвергенции бетонной крепи ствола при пересечении слоев породного массива с различными физико-механическими свойствами получены прогнозные оценки предельного времени эксплуатации армировки, после которого потребуется проведение ремонтных работ.
Таким образом, комплексная оценка деформирования жесткой армировки при конвергенции бетонной крепи ствола позволяет производить корректные расчеты по определению параметров рациональных схем конструкций армировки и крепи стволов, расположенных в соляном массиве.
Литература
- Манец И.Г., Снегирев Ю.Д., Паршинцев В.П. Техническое обслуживание и ремонт шахтных стволов. М.: Недра, 1987. 327 с.
- Gerdemeli I., Candas A., Unalan M. Design of Mine Shaft Elevator // Scientific Proceedings IX International Congress “Machines, Technologies, Materials”, 19-21 September 2012, Varna, Bulgaria. Sofia, 2012. Vol. 2. P. 117-120.
- Плешко М.С., Насонов А.А., Ягодкин Ф.И., Привалов А.А. Некоторые вопросы повышения эффективности проектирования, строительства и реконструкции вертикальных стволов // Горный информационно-аналитический бюллетень. 2017. № 8. С. 179-186. DOI: 10.25018/0236-1493-2017-8-0-179-186
- Страданченко С.Г., Прокопов А.Ю., Ткачева К.Э. Вероятностный подход к определению временных нагрузок на жесткую армировку вертикальных стволов // Горный информационно-аналитический бюллетень. 2012. № 8. С. 61-68.
- Тарасов В.В., Пестрикова В.С., Русаков М.И. Жизненные циклы комплекса сооружений шахтных стволов Верхнекамского месторождения. Новосибирск: Наука, 2021. 230 с.
- Ягодкин Ф.И., Прокопов А.Ю., Прокопова М.В. Ремонт крепи вертикальных шахтных стволов // Известия Тульского государственного университета. Науки о Земле. 2017. Вып. 3. С. 195-208.
- Самуся В.И., Ильин С.Р., Ильина И.С., Ильина С.С. Факторы нарушения устойчивости работы системы сосуд-армировка в сложных горно-геологических условиях вертикальных стволов // Вестник Пермского национального исследовательского политехнического университета. Геология. Нефтегазовое и горное дело. 2015. № 17. С. 72-80. DOI: 10.15593/2224-9923/2015.17.8
- Тарасов В.В., Аптуков В.Н. Мониторинг деформации бетонной крепи шахтных стволов с помощью лазерного сканирования // Физико-технические проблемы разработки полезных ископаемых. 2022. № 5. С. 188-195. DOI: 10.15372/FTPRPI20220518
- Трифанов Г.Д., Микрюков А.Ю. Повышение эффективности эксплуатации шахтных подъемных установок на основе мониторинга плавности движения скипов // Актуальные проблемы повышения эффективности и безопасности эксплуатации горношахтного и нефтепромыслового оборудования. 2016. Т. 1. С. 49-54.
- Tarasov V.V., Aptukov V.N., Pestrikova V.S. Deformation and failure of concrete lining in vertical shaft at intersections with horizontal tunnels // Journal of Mining Science. 2020. Vol. 56. Iss. 5. P. 726-731. DOI: 10.1134/S1062739120057056
- Константинова С.А., Крамсков Н.П., Соловьев В.А. Некоторые проблемы механики горных пород применительно к отработке алмазных месторождений Якутии. Новосибирск: Наука, 2011. 223 с.
- Карасев М.А., Буслова М.А., Вильнер М.А., Нгуен Т.Т. Методика прогноза напряженно-деформированного состояния крепи вертикального ствола на участке сопряжения с горизонтальной выработкой в соляных породах // Записки Горного института. 2019. Т. 240. С. 628-637. DOI: 10.31897/PMI.2019.6.628
- Дубинин М.В., Дворников В.И. Конечноэлементное моделирование напряженно-деформированного состояния жесткой армировки стволов под действием эксплуатационных нагрузок со стороны подъемных сосудов // Актуальные проблемы повышения эффективности и безопасности эксплуатации горношахтного и нефтепромыслового оборудования. 2014. Т. 1. С. 55-60.
- Балек А.Е., Ефремов Е.Ю. Исследование напряженно-деформированного состояния сопряжения ствола с околоствольными выработками маркшейдерскими методами // Известия Тульского государственного университета. Науки о Земле. 2019. Вып. 2. С. 267-279. DOI: 10.25635/IM.2019.29.37273
- Прокопов А.Ю., Прокопова М.В. Проектирование армировки глубоких вертикальных стволов на основе закономерностей функционирования системы «подъемный сосуд – армировка – ствол» // Горный информационно-аналитический бюллетень. 2012. № 7. С. 78-82.
- Kopytov A.I., Pershin V.V., Voitov M.D., Wetti A.A. The Improvement of the Bunton Construction of Mine-shaft Equipment // The 8th Russian-Chinese Symposium. Coal in the 21st Century: Mining, Processing and Safety, 10-12 October 2016, Kemerovo, Russia. Atlantis Press, 2016. P. 108-110. DOI: 10.2991/coal-16.2016.21
- Сентябов С.В., Селин К.В., Карамнов Д.В. Уточнение и мониторинг параметров вертикальных деформаций оси шахтных стволов на выработанное пространство // Проблемы недропользования. 2020. № 2 (25). С. 108-115. DOI: 10.25635/2313-1586.2020.02.108
- Ilin S.R., Samusia V.I., Ilina I.S., Ilina S.S. Influence of Dynamic Processes in Mine Hoists on Safety of Exploitation of Shafts with Broken Geometry // Науковий вiсник Нацiонального гiрничого унiверситету. 2016. № 3. С. 48-53.
- Wolny S., Matachowski F. Analysis of Loads and Stresses in Structural Elements of Hoisting Installations in Mines // Engineering Transaction. 2010. Vol. 58. № 3-4. P. 153-174.
- Коднянко Е.В. Исследование изнашивания профиля проводников шахтного ствола // Инновации и перспективы развития горного машиностроения и электромеханики: IPDME-2021: Сборник тезисов VIII Международной научно-практической конференции, 22-23 апреля 2021 г., Санкт-Петербург, Россия. СПб.: Санкт-Петербургский горный университет, 2021. С. 189-191.
- Xiao Xing-ming, Li Zhan-fang, Zhang Jun. Study on fault mechanism of shaft hoist steelwork // The 6th International Conference on Mining Science & Technology, 18-20 October 2009, Xuzhou, China. Procedia Earth and Planetary Science, 2009. Vol. 1. Iss. 1. P. 1351-1356. DOI: 10.1016/j.proeps.2009.09.208
- Трифанов Г.Д., Князев А.А., Филатов А.П., Лаук В.В. Опыт эксплуатации шахтных подъемных установок, оснащенных системами непрерывного контроля // Безопасность труда в промышленности. 2019. № 6. С. 52-58. DOI: 10.24000/0409-2961-2019-6-52-58
- Hanna M., Lloyd A., Tikka T. Improving conveyance side slipper plate design to accommodate higher impact bunton force // Building Tomorrow’s Society, 13-16 June 2018, Fredericton, Canada. Canadian Society for Civil Engineering, 2018. P. ST49-1 – ST49-10.
- Зеленко А.В., Горбач А.Н. Непрерывный мониторинг безопасного движения подъемных сосудов шахтных стволов // Актуальные проблемы повышения эффективности и безопасности эксплуатации горношахтного и нефтепромыслового оборудования: Материалы VI Международной научно-практической конференции «Горная и нефтяная электромеханика-2019», 21-24 октября 2019 г., Пермь, Россия. Пермь: Изд-во Пермского национального исследовательского политехнического университета, 2019. Т. 1. С. 37-43.
- Nikolaitchik M. Determination of skip force effect on guides in mine shaft // Ukrainian School of Mining Engineering, 7-11 September 2020, Berdiansk, Ukraine. E3S Web of Conferences, 2020. Vol. 201. № 01017. DOI: 10.1051/e3sconf/202020101017
- Микрюков А.Ю., Каменских Я.В. Обследование и оценка технического состояния подъемных сосудов // Актуальные проблемы повышения эффективности и безопасности эксплуатации горношахтного и нефтепромыслового оборудования: Материалы VI Международной научно-практической конференции «Горная и нефтяная электромеханика-2019», 21-24 октября 2019 г., Пермь, Россия. Пермь: Изд-во Пермского национального исследовательского политехнического университета, 2019. Т. 1. С. 69-75.
- Пестрикова В.С. Алгоритм расчета долговечности жестких армировок шахтных стволов, эксплуатируемых в условиях Верхнекамского месторождения калийных солей // Известия Тульского государственного университета. Науки о Земле. 2019. Вып. 4. С. 332-339.
- Jiannan Yao, Xiaojie Deng, Chi Ma, Tong Xu. Investigation of Dynamic Load in Superdeep Mine Hoisting Systems Induced by Drum Winding // Shock and Vibration. 2021. Vol. 2021. № 4756813. DOI: 10.1155/2021/4756813
- Качурин Н.М., Афанасьев И.А., Пестрикова В.С., Стась П.П. Взаимодействия вертикальных стволов с породными массивами при восстановлении крепи и армировки // Известия Тульского государственного университета. Науки о Земле. 2020. Вып. 3. С. 290-303.
- Журавков М.И., Николайчик М.А. Конечно-элементное моделирование взаимодействия подъемного сосуда с конструктивными элементами шахтного ствола // Горная механика и машиностроение. 2021. № 4. С. 15-21.
- Николайчик М.А., Журавков М.И. Математическое моделирование состояния ответственных элементов шахтного подъемного комплекса // Проблемы безопасности на транспорте: Материалы XII Международной научно-практической конференции, посвященной 160-летию Белорусской железной дороги, 24-25 ноября 2022 г.: в 2 ч. Гомель, Беларусь. Белорусский государственный университет транспорта, 2022. Ч. 2. С. 228-230.
- Jakubowski J., Fiolek P. Evaluation of Stiffness and Dynamic Properties of a Mine Shaft Steelwork Structure through In Situ Tests and Numerical Simulations // Energies. 2021. Vol. 14. Iss. 3. № 664. DOI: 10.3390/en14030664
- Fiolek P., Jakubowski J. Assessment of the Bending Moment Capacity of Naturally Corroded Box-Section Beams // Materials. 2021. Vol. 14. Iss. 19. № 5766. DOI: 10.3390/ma14195766
- Fiolek P., Jakubowski J. Local buckling of highly corroded hot-rolled box-section beams // Journal of Constructional Steel Research. 2019. Vol. 157. P. 359-370. DOI: 10.1016/j.jcsr.2019.03.009
- Jakubowski J., Fiołek P. Probabilistic structural reliability assessment of underground shaft steelwork // Tunnelling and Underground Space Technology. 2022. Vol. 130. № 104755. DOI: 10.1016/j.tust.2022.104755
- Лалин В.В., Кушова Д.А. Геометрически нелинейное деформирование и устойчивость плоских упругих стержней с учетом жесткостей на растяжение-сжатие, сдвиг и изгиб // International Journal for Computational Civil and Structural Engineering. 2013. Vol. 9. Iss. 4. P. 178-185.
- Прасолов В.В., Соловьев Ю.П. Эллиптические функции и алгебраические уравнения. М.: Изд-во Московского центра непрерывного математического образования, 2022. 312 с.
- Самуся В.И., Ильина И.С., Ильина С.С. Компьютерное моделирование и исследование динамики систем «сосуд-армировка» в стволах с нарушенной геометрией // Вестник ПНИПУ. Геология. Нефтегазовое и горное дело. 2016. Т. 15. № 20. С. 277-285. DOI: 10.15593/2224-9923/2016.20.8
- Тутышкин Н.Д., Гвоздев А.Е., Трегубов В.И. и др. Комплексные задачи теории пластичности. Тула: Изд-во Тульского государственного университета, 2015. 408 с.
- Бровко Г.Л. Подходы к постановкам и методам решения краевых задач механики деформируемого твердого тела // Известия МГТУ «МАМИ». 2013. Т. 7. № 3-1. С. 46-65. DOI: 10.17816/2074-0530-67989
- Морозов Е.М., Муйземнек А.Ю., Шадский А.С. ANSYS в руках инженера: Механика разрушения. М.: ЛЕНАНД, 2014. 456 с.
