Математическое моделирование электрического поля внутритрубного  диагностического зонда катодно-поляризуемого трубопровода

В. Н. Кризский; О. В. Косарев; П. Н. Александров; Я. А. Лунтовская

Том 265

Страницы:

156-164

Скачать том:

RUS ENG

Научная статья

Энергетика

Математическое моделирование электрического поля внутритрубного диагностического зонда катодно-поляризуемого трубопровода

Авторы:

В. Н. Кризский¹

О. В. Косарев²

П. Н. Александров³

Я. А. Лунтовская⁴

Об авторах

1 — д-р физ.-мат. наук профессор Санкт-Петербургский горный университет ▪ Orcid
2 — канд. техн. наук Санкт-Петербургский горный университет ▪ Orcid
3 — д-р физ.-мат. наук главный научный сотрудник Институт физики Земли им. О.Ю.Шмидта РАН ▪ Orcid ▪ Elibrary ▪ Scopus
4 — аспирант Санкт-Петербургский горный университет ▪ Orcid

Дата отправки:

2022-07-10

Дата принятия:

2023-06-20

Дата публикации:

2024-02-29

Аннотация

Рассмотрена математическая модель внутритрубного контроля состояния сопротивления изоляции катодно-поляризуемых магистральных продуктопроводов по данным электрометрии. Актуальность работы обусловлена возможностью создания внутритрубных индикаторов дефектов внутренней изоляции магистральных трубопроводов для хорошо проводящих электрический ток транспортируемых жидкостей и расширения за счет этой информации функционала систем мониторинга и управления станций катодной защиты магистральных продуктопроводов. Отличительные особенности математической модели: учет влияния электропроводности транспортируемой жидкости на распределение электрических полей; учет влияния сопротивления внешнего и внутреннего изоляционного покрытия; использование электрического поля внутритрубного диагностического зонда для контроля качества внутренней изоляции. Практическая значимость заключается в развитии методов моделирования управляющих подсистем электрохимических систем защиты магистральных трубопроводов от коррозии и разработке специального математического и алгоритмического обеспечения систем мониторинга и управления режимами работы станций катодной защиты магистральных продуктопроводов.

Ключевые слова:

математическое моделирование электрического поля катодная электрохимическая защита магистрального трубопровода внешнее и внутреннее изоляционное покрытие внутритрубная диагностика коррозия метод фиктивных источников градиент электрического поля вычислительный эксперимент электрическое зондирование

Введение

Магистральные трубопроводы (МТ) подвержены коррозии, что является основной причиной их аварий и простоев [1, 2]. Коррозия возникает из-за влияния механических примесей [3-5], блуждающих токов различной природы [6], деформации труб и вмещающего грунта [7-9], наличия дефектов внутреннего и внешнего изоляционного покрытия и др. Для диагностики состояния трубопроводов широко применяются магнитометрические и ультразвуковые методы [10, 11]. Ультразвуковые методы неразрушающего контроля развиваются как в направлении оптимизации количества и пространственного расположения датчиков [12], так и в направлении усложнения обработки отраженных сигналов [13-15]. Контроль состояния внешней изоляции [16, 17], как правило, выполняется вручную с использованием специального оборудования [18-20], но интенсивно развиваются и дистанционные методы неразрушающего контроля [21]. Оценить качество внутритрубной изоляции снаружи трубы затруднительно в силу экранирующих возбуждаемое поле свойств металла трубы. Решением в таких случаях является использование внутритрубных снарядов (зондов) [22]. При внутритрубной диагностике используются магнитометрические [23] и ультразвуковые способы оценки качества металла трубы. Применение внутритрубного источника постоянного электрического тока в хорошо проводящих ток транспортируемых средах (соляные растворы, вода, некоторые продукты многотоннажных химических производств и пр.) и водонефтяных средах [24, 25] делает возможным исследование взаимовлияния качества внутренней изоляции и градиента измеряемого зондом электрического поля. Такая оперативная оценка качества внутренней изоляции способствует развитию специального математического и алгоритмического обеспечения систем мониторинга и управления станций катодной защиты (СКЗ) магистральных продуктопроводов.

Цель работы – разработка математической модели внутритрубного контроля состояния сопротивления изоляции катодно-поляризуемых магистральных продуктопроводов по данным электрометрии. Актуальность работы обусловлена возможностью создания внутритрубных индикаторов дефектов внутренней изоляции МТ и расширения за счет этой информации функционала систем мониторинга и управления СКЗ магистральных продуктопроводов. Решены следующие задачи: построенная дифференциальная математическая модель электрического поля СКЗ и внутритрубного электрического зонда методом фиктивных источников сведена к дискретной модели в виде системы линейных алгебраических уравнений (СЛАУ); методом вычислительного эксперимента исследовано влияние нарушения внутренней изоляции на градиент электрического поля внутритрубного зонда.

Методы

Обеспечение требуемого качества защиты эксплуатируемого нефтегазового оборудования [26-28] от коррозии в том числе подразумевает поддержание необходимого уровня защитного катодного потенциала на поверхности металла. Для решения этой задачи применяются современные вычислительные технологии, включая нейронные сети [29]. Математическая модель катодно-поляризуемого МТ должна описывать распределение токов и потенциалов по всей протяженности защищаемого СКЗ участка. Конкретная реализация модели позволит рассчитать величины токов и напряжений в трубе и на границах «труба – грунт», «труба – транспортируемая жидкость» [30-32]. Исходными данными для расчетов служат электрические свойства всех сред распространения токов, сила тока СКЗ, геометрические характеристики МТ, пространственные координаты МТ, анодного заземлителя и точки дренажа тока. В силу невозможности точного определения во времени и в пространстве всех физических величин, описывающих реальную эксплуатацию магистрали, абсолютно точное описание такой системы принципиально невозможно [16]. Тем не менее, как показывает анализ научных исследований [17, 33], в расчетах используется такая модель вмещающей МТ среды, как однородное изотропное полупространство с усредненной (и постоянной) удельной электропроводностью грунта. Поэтому для достижения цели необходимо разработать адекватную математическую модель прямой задачи распределения электромагнитного поля постоянного электрического тока системы катодной защиты МТ в однородной среде вида «грунт – внешняя изоляция – металл – внутренняя изоляция – транспортируемая жидкость – зонд» и провести вычислительный эксперимент, исследующий влияние переходного сопротивления внутренней изоляции на токораспределение в системе.

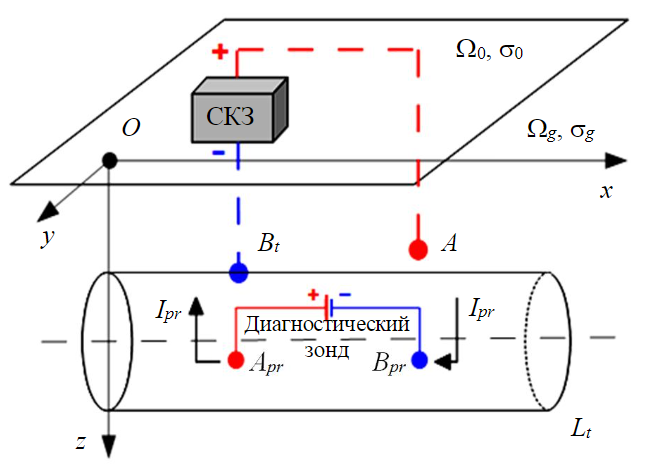
Рис.1. Включение диагностического зонда в схему катодной защиты МТ в однородном полупространстве

Пусть дано однородное пространство (рис.1), разделенное плоской границей на два полупространства, – Ω₀ (воздух) с удельной электропроводностью σ₀ = 0 См/м и Ω_g (грунт) с заданной постоянной удельной электропроводностью заполняющего вещества σ_g = const См/м. Предположим, что в полупространстве Ω_g расположен прямолинейный трубопровод длины L_t. Внутри трубопровода в транспортируемой жидкости с удельной электропроводностью σ_l находится диагностический зонд (A_pr – B_pr), инжектирующий постоянный электрический ток силы I_pr. Станция катодной защиты обеспечивает постоянный защитный ток I_a, стекающий через точечный анод, находящийся в точке А(x_А, y_А, z_А) полупространства Ω_g. Дренаж защитного тока с металла трубы осуществляется в точке B_t. Координаты точек А и B_t в декартовой системе координат известны. Начало системы координат выбрано на поверхности «воздух – грунт». Ось Ox направлена параллельно оси трубопровода, ось Oz – вниз.

Математическая модель, описывающая распределение потенциала поля постоянного электрического тока в системе в произвольной точке пространства P(x_P, y_P, z_P), имеет вид:

\begin{matrix} Δ U_{g} (P) = - \frac{I_{a}}{σ_{g}} δ (P - A); (1) \\ Δ U_{m} (P) = 0; Δ U_{l} (P) = - I_{p r} (δ (P - A_{p r}) - δ (P - B_{p r})); (2) \\ {\frac{\partial U_{g} (P)}{\partial z}|}_{z = 0} = 0; U_{g} (P) \to 0, P \to \infty; (3) \\ {\frac{\partial U_{m}}{\partial x}|}_{x = 0; L_{t}} = 0; {\frac{\partial U_{l}}{\partial x}|}_{x = 0; L_{t}} = 0; (4) \\ {U_{g} (P) - C_{g m} (P) σ_{g} (P) \frac{\partial U_{g} (P)}{\partial n}|}_{S_{g m}} = U_{m} (P); (5) \\ {U_{l} (P) + C_{m l} (P) σ_{l} (P) \frac{\partial U_{l} (P)}{\partial n}|}_{S_{m l}} = U_{m} (P); (6) \\ {[\frac{\partial U_{m} (P)}{\partial x}]|}_{B_{t}} = \frac{I_{a}}{σ_{m} S_{m}}, (7) \end{matrix}

где С_gm(P) – переходное сопротивление, отражающее состояние внешнего изоляционного покрытия трубы в точке P, Ом·м²; S_gm – площадь внешней поверхности трубы, м²; n – нормаль к поверхности трубы; С_ml(P) – переходное сопротивление, отражающее состояние внутреннего изоляционного покрытия в точке P, Ом·м²; S_ml – площадь внутренней поверхности трубы, м²; S_m – площадь поперечного сечения металла, м²; σ_m– удельная электрическая проводимость металла трубы, См/м; индексы: g – грунт; m – металл трубы; l – транспортируемая жидкость; gm – граница «грунт – металл»; ml – граница «металл – жидкость».

Уравнения в математической модели (1)-(7) описывают следующие процессы: (1) – распределение потенциала U_g электрического тока в грунте; (2) – распределение потенциала U_m электрического тока в металле трубы и потенциала U_l в транспортируемой жидкости; (3) – условие непротекания тока через границу «воздух – грунт» и условие регулярности решения на бесконечности; (4) – условие непротекания тока на торцевых границах для металла трубы и транспортируемой жидкости; (5) – условие протекания тока через границу «грунт – металл»; (6) – условие протекания тока через границу «металл – жидкость»; (7) – условие подключения катодной станции к трубопроводу в точке дренажа.

Для решения задачи применим метод фиктивных источников [17, 33]. Представим МТ в виде последовательности М_t штук сегментов одинаковой длины (рис.2). Для каждого такого сегмента будем считать, что рассматриваемые электрические параметры постоянны и равны среднему значению на своем сегменте. Для каждого сегмента i (i = 1 ... M_t) на трубопроводе рассмотрим усредненные значения: $U_{g}^{i}$ – потенциал в грунте на границе «грунт – металл», В; $U_{m}^{i}$ – потенциал в металле трубы, В; $U_{l}^{i}$ – потенциал в жидкости, В; $I_{g m}^{i}$ – сила тока, втекающего из грунта в металл трубы через боковую поверхность, А; $I_{m}^{i}$ – продольный ток в металле трубы, А; $I_{m l}^{i}$ – сила тока на границе «металл – жидкость», А; $I_{l}^{i}$ – продольный ток в жидкости, А. Диагностический зонд является источником постоянного тока силы I_pr между электродами, расположенными в точках A_pr и B_pr.

Рис.2. Фрагмент дискретной модели трубопровода 1-2 – участки с нарушенной изоляцией: 1 – внешней; 2 – внутренней; 3 – участок с точкой дренажа *B_t* защитного тока *I_a*

Каждый сегмент трубы формирует фиктивные точечные источники и (или) стоки тока. Для каждого фиктивного источника и (или) стока тока вытекающие и (или) втекающие в него токи описываются законами Кирхгофа:

\begin{matrix} I_{g m}^{i} + I_{m}^{i - 1} - I_{m}^{i} - I_{m l}^{i} - I_{a} δ (B_{m}^{i}, B_{t}) = 0; (8) \\ i = \bar{1, M_{t}}, I_{m}^{0} = 0, I_{m}^{M_{t}} = 0; \\ I_{m l}^{i} + I_{l}^{i - 1} - I_{l}^{i} + δ (B_{l}^{i}, A_{p r}) I_{p r} - δ (B_{l}^{i}, B_{p r}) I_{p r} = 0; (9) \\ i = \bar{1, M_{t}}, I_{l}^{0} = 0, I_{l}^{M_{t}} = 0, \end{matrix}

где $B_{m}^{i}$ – координаты средней точки в металле i-го сегмента; A_pr и B_pr – текущие положения электродов диагностического зонда внутри транспортируемой жидкости в трубе, отнесенные к средним точкам сегментов в жидкости.

В равенствах (8) и (9) учтены условия (4) непротекания тока на торцевых границах для металла трубы и транспортируемой жидкости.

Дискретные формулы закона Ома для токов между парами соседних сегментов описываются уравнениями:

\begin{matrix} U_{m}^{i + 1} - U_{m}^{i} = - R_{m} I_{m}^{i}, i = \bar{1, M_{t} - 1}, R_{m} = \frac{L_{t}}{M_{t} σ_{m} S_{m}}; (10) \\ U_{l}^{i + 1} - U_{l}^{i} = - R_{l} I_{l}^{i}, i = \bar{1, M_{t} - 1}, R_{l} = \frac{L_{t}}{M_{t} σ_{l} S_{l}}, (11) \end{matrix}

где S_l – площадь поперечного сечения транспортируемой жидкости.

Дискретный аналог формул граничных условий третьего рода на границах «грунт – металл» и «металл – жидкость» описывается равенствами:

\begin{matrix} U_{g}^{i} - \frac{C_{g m}^{i} I_{g m}^{i}}{S_{g m}^{i}} = U_{m}^{i}, i = \bar{1, M_{t}}; (12) \\ U_{l}^{i} + \frac{C_{m l}^{i} I_{m l}^{i}}{S_{m l}^{i}} = U_{m}^{i}, i = \bar{1, M_{t}} . (13) \end{matrix}

Потенциал электрического тока в произвольной точке вмещающего трубопровод однородного полупространства, согласно принципу суперпозиции полей, будет формироваться точечным анодным источником СКЗ А и фиктивными источниками по числу сформированных сегментов трубы. Потенциал описывается следующим равенством:

U_{g} (P) = I_{a} G (P, A) - \sum_{i = 1}^{M_{t}} I_{g m}^{i} G (P, B_{m}^{i}), (14)

где G(P, Q) – функция Грина [30] вмещающего однородного полупространства – функция, вычисляющая значение потенциала поля электрического тока в точке P(x_P, y_P, z_P) полупространства, при нахождении точечного источника электрического тока единичной интенсивности в точке Q(x_Q, y_Q, z_Q).

Дискретная модель (8)-(14) при подстановке в (14) точек грунта $P = B_{g}^{k}, k = \bar{1, M_{t}}$ , расположенных рядом с границей «грунт – металл», представляет собой СЛАУ со следующими неизвестными: U_m, U_g, U_l, I_gm, I_m, I_l, I_ml. Здесь каждое искомое неизвестное представляет собой вектор усредненных на сегменте значений тока или напряжения. Расширенная матрица СЛАУ имеет размер (7M_t – 2)´(7M_t – 1). Решение СЛАУ дает значения искомых параметров тока и напряжения для каждого дискретного сегмента. Таким образом, исходная дифференциальная математическая модель (1)-(7), описывающая распределение потенциала поля постоянного электрического тока в системе, методом фиктивных источников сведена к СЛАУ (8)-(14).

Вычислительный эксперимент построен по следующей методике. На первом этапе определялись значения электрического поля зонда в транспортируемой жидкости при ненарушенной внутренней и внешней изоляции и нулевом токе СКЗ I_a = 0 А. Назовем полученное поле «нормальным» полем зонда.

На втором этапе рассчитывалось «рабочее» электрическое поле – поле зонда при нарушении переходного сопротивления внутренней и (или) внешней изоляции на сегменте трубы и при включенном токе СКЗ. Из «рабочего» поля затем вычиталось «нормальное» поле. Результат этапа – «аномальное» поле электрического тока.

На этапах 1 и 2 имитировалось перемещение внутритрубного зонда в трубе. Размер внутритрубного зонда задавался равным длине семи сегментов дискретной модели трубопровода (7 м для вычислительного эксперимента). Рассчитывалось 15 последовательных положений зонда, при которых середина зонда имела смещение от середины «дефектного» сегмента в диапазоне отрезка [–7; +7] сегментов.

На третьем этапе рассчитывался градиент поля между фиксированными внутренними точками зонда, имитирующими положение его измерительных датчиков. Исходные данные вычислительного эксперимента приведены в таблице.

Исходные данные вычислительного эксперимента

Параметр	Обозначение	Значение
Длина МТ, м	L_t	10000
Количество сегментов, шт.	M_t	10000
Длина одного сегмента модели, м	l	1
Глубина залегания МТ, м	H_t	2,0
Диаметр МТ, м	D_t	0,53
Толщина стенки МТ, м	h_t_m	0,008
Координата точечного анода А, м	(x_A, y_A, z_A)	(5000; 350; 25)
Координата точки дренажа B_t, м	(x_Bt, y_Bt, z_Bt)	(5000; 5,0; 2,265)
Номер сегмента точки дренажа B_t	–	5001
Номер сегмента c дефектом внешней изоляции	–	2501
Номер сегмента c дефектом внутренней изоляции	–	2501
Постоянный ток СКЗ, A	I_a	1,0
Постоянный ток диагностического зонда, A	I_pr	1,0
Удельная электропроводимость металла МТ, См/м	s_m	4,082∙10⁶
Удельная электропроводимость грунта, См/м	s_g	0,01
Удельная электропроводимость жидкости, См/м	s_l	1,04
Переходное сопротивление внешней изоляции МТ, Ом∙м²	C_gt	14000
Переходное сопротивление внутренней изоляции МТ, Ом∙м²	C_ml	10000
Переходное сопротивление внешней изоляции МТ в «дефектном» сегменте № 2501, Ом∙м²	C_{gt_}₂₅₀₁	1,4
Переходное сопротивление внутренней изоляции МТ в «дефектном» сегменте № 2501, Ом∙м²	C_{ml_}₂₅₀₁	1,0

Вычислительный эксперимент выполнялся в среде Matlab с использованием подгружаемого модуля работы с разреженными матрицами. Для решения СЛАУ применялись операции левого деления матриц. На рис.3 показана структура расширенной матрицы СЛАУ для одного из положений зонда в трубе, где синим цветом представлены положения ненулевых элементов системы, через nz обозначено количество ненулевых элементов расширенной матрицы. Плотность заполнения расширенной матрицы составляет около 2 %.

Полная матрица СЛАУ для количества сегментов M_t = 10000 в формате данных double имеет размер порядка 36 Гб. Задача решена на базе компьютера с процессором Intel I5 10-го поколения и ОЗУ 12 Гб в пакете Matlab с использованием аппарата разреженных матриц. Расчет СЛАУ для одного положения зонда выполняется 10-11 ч.

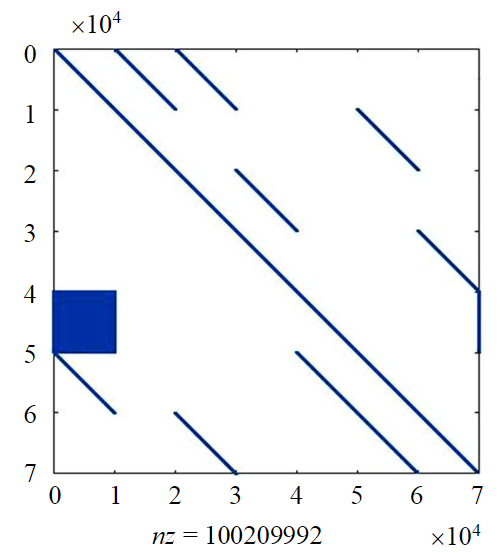
Рис.3. Структура расширенной матрицы СЛАУ

Рис.4. Распределение потенциала поля электрического тока в транспортируемой жидкости при нулевом положении зонда 1 – «нормальное»; 2 – «аномальное»; 3 – «рабочее» поле

Распределение потенциала «нормального» поля зонда (рис.4, кривая 1), суперпозиции полей СКЗ + зонда для «дефектной» по изоляционному покрытию трубы (рис.4, кривая 2) и «аномального» (разность между «рабочим» и «нормальным», рис.4, линия 3) поля в транспортируемой жидкости. По оси Ох взят отрезок, включающий в себя сегмент с дефектной изоляцией (№ 2501). Нарушение изоляции на сегменте трубы влечет перераспределение электрического поля зонда за счет утечки части тока зонда в металл трубы.

Для этого случая положение зонда в трубе фиксировано – середина зонда приходится на середину «дефектного» сегмента (нулевое положение зонда dz = 0). На рис.5 показаны фрагменты «аномального» поля, вычисленные при некоторых смещениях внутритрубного зонда. Диапазон перемещений центрального сегмента зонда – в диапазоне отрезка [–7; +7] сегментов трубы относительно сегмента с нарушенной изоляцией.

Практический интерес представляет определение номера сегмента с дефектной изоляцией при движении диагностического зонда внутри МТ. При этом конкретное значение потенциала в данном случае вторично по сравнению с характером изменения поля при прохождении «дефектного» сегмента. Поэтому на третьем этапе вычислительного эксперимента рассчитан градиент поля между двумя симметричными относительно центра сегментами диагностического зонда (двумя измерительными датчиками). На рис.6 показаны градиенты «аномального» поля, построенные на основе разностей потенциалов между симметричными сегментами зонда, при движении зонда внутри трубопровода. На рисунке z_х обозначены используемые для нахождения конечных разностей сегменты зонда (х – смещение сегмента относительно среднего сегмента z₀). Графики градиентов симметричны относительно «дефектного» сегмента и при совпадении центра зонда с дефектным сегментом обращаются в ноль. Эти свойства градиента могут быть использованы как признаки обнаружения «дефектного» сегмента трубы.

Обсуждение результатов

Предложенная в работе модель распределения потенциала поля постоянного электрического тока внутритрубного зонда катодно-поляризуемого трубопровода позволяет обнаружить нарушение внутреннего изоляционного слоя. Включение в модель диагностического зонда решает две задачи. Во-первых, токи, протекающие внутри транспортируемой жидкости и перетекающие из жидкости в металл трубы, могут быть увеличены за счет вариации силы тока зонда до величин, регистрируемых приборами. Во-вторых, одновременное отслеживание положения диагностического зонда в МТ и регистрация потенциалов в жидкости позволяют локализовать место нарушения внутритрубной изоляции с точностью, определяемой характеристиками датчика измерения потенциалов тока (градиента тока) в жидкости и датчика определения положения зонда в трубе. Определение местоположения зонда в разветвленной сети трубопроводов [34, 35] представляет одну из важных независимых подзадач. Определение координат сегмента с нарушенной изоляцией позволяет включить способ электрического зондирования в интеллектуальное аналитическое ядро автоматизированных систем управления электрохимической защитой магистральных продуктопроводов.

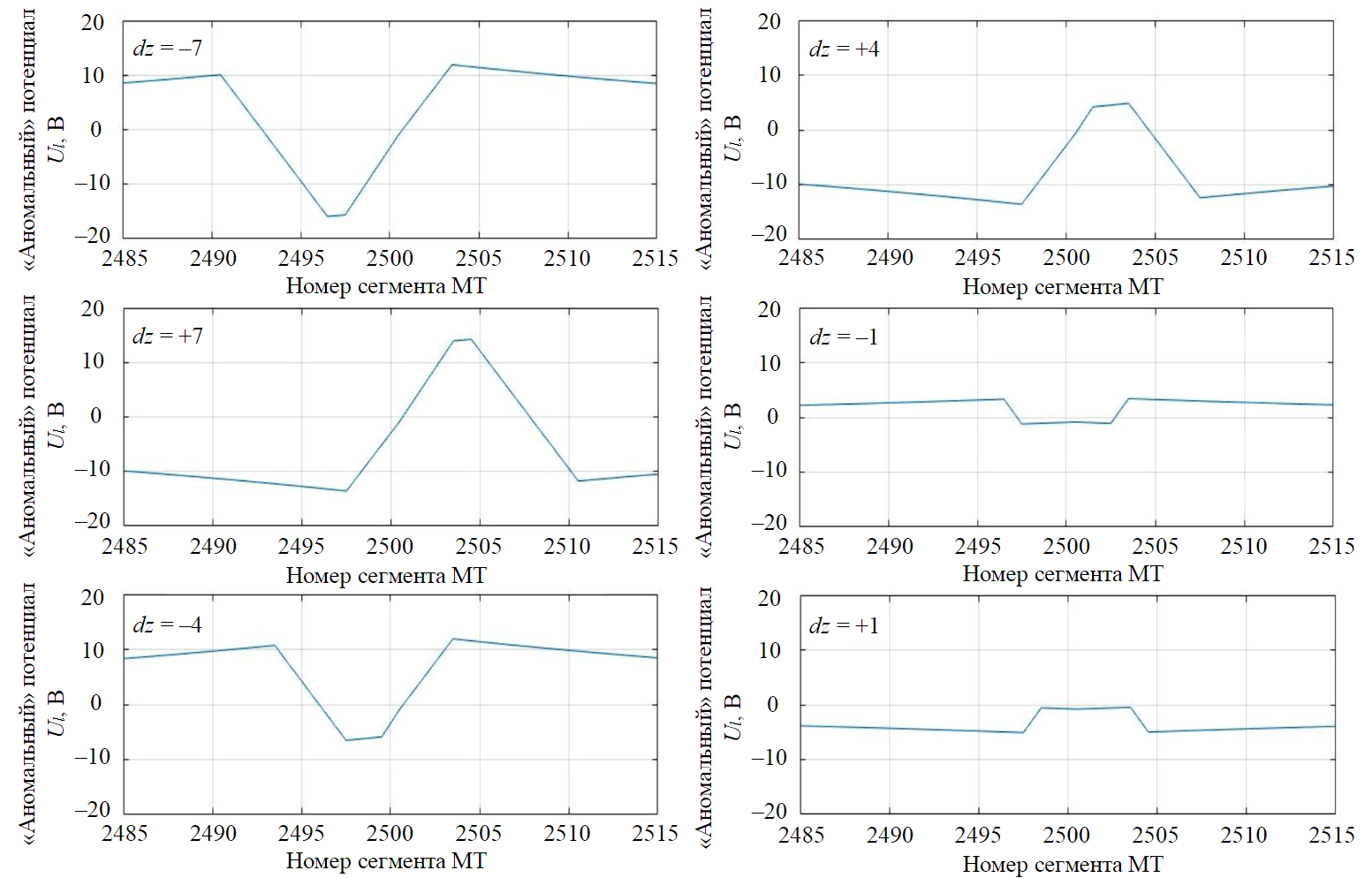
Рис.5. Эпюры «аномального» потенциала *U_l* в транспортируемой жидкости

Включение в модель внутритрубного источника постоянного тока потенциально расширяет класс исследуемых трубопроводов. В их число могут быть отнесены трубопроводы, эксплуатируемые и без использования систем катодной защиты.

Предложенная в работе модель в виде СЛАУ (8)-(14) и способ ее решения позволяют достичь дискретизации длины продуктопровода в 1 м. Это на порядок превосходит параметры дискретизации, достигнутые в работе [30] и исследованиях других коллективов в этом направлении [33, 36].

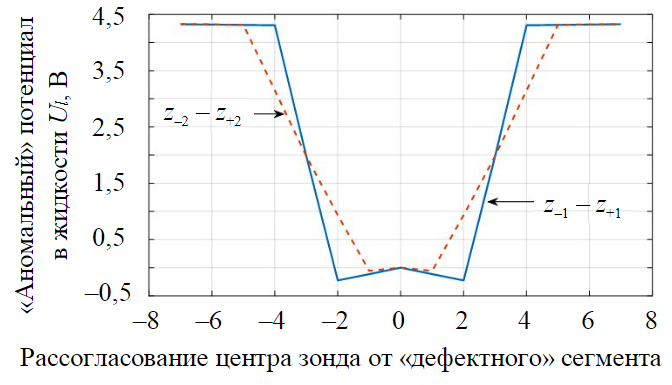
Рис.6. Распределение градиента поля в жидкости при движении зонда

Заключение

Предложенная в работе математическая модель описывает распределение потенциала поля постоянного электрического тока в системе электрохимической защиты МТ. Полученные результаты для ряда частных случаев согласуются с ранее известными [17, 30, 36]. Отличительными особенностями модели являются: учет влияния электропроводности транспортируемой жидкости и переходного сопротивления внутреннего изоляционного покрытия на распределение электрических полей; использование электрического поля внутритрубного диагностического зонда для контроля качества внутренней изоляции. Практическая значимость заключается в развитии методов моделирования систем электрохимических защиты МТ от коррозии и разработке специального математического и алгоритмического обеспечения подсистем мониторинга и управления СКЗ магистральных продуктопроводов. Длина одного сегмента продуктопровода в модели равна 1 м, что выше известных решений. Такая точность локализации дефектов покрытия делает целесообразным использование автономных роботизированных комплексов для обследования продуктопроводов.

Литература

Нишкевич Ю.А., Козлов И.А. Коррозия: способы борьбы с коррозией в нефтяной промышленности. М.: НИЦ ИНФРА-М, 88 с. DOI: 10.12737/monography_59a018d0867c99.11635048
Мустафин Ф.М., Чэнь Цюнь, Мустафин О.Ф. и др. Пассивная защита трубопроводов от коррозии // Neftegaz.RU. 2020. № 2. С. 86-90.
Бурков П.В., Бурков В.П., Фатьянов Д.С., Тимофеев В.Ю. Исследование напряженно-деформированного состояния промысловых трубопроводов подвергшихся воздействию ручейковой коррозии // Вестник Кузбасского государственного технического университета. 2018. № 3. С. 5-12. DOI: 10.26730/1999-4125-2018-3-5-12
Исмайылов Г.Г., Искендеров Э.Х., Исмайылова Ф.Б. Проблемы гидродинамической коррозии в мультифазных трубопроводах // Физикохимия поверхности и защита материалов. 2021. Т. № 1. С. 106-112. DOI: 10.31857/S0044185621010125
Болобов В.И., Попов Г.Г. Методика испытаний трубопроводных сталей на стойкость к «ручейковой» коррозии // Записки Горного института. 2021. Т. С. 854-860. DOI: 10.31897/PMI.2021.6.7
Агиней Р.В., Исупова Е.В., Гуськов С.С., Мусонов В.В. Теоретическая оценка скорости коррозии магистральных трубопроводов, вызванной влиянием геомагнитно-индуцированного источника блуждающего тока // Наука и техника в газовой промышленности. 2020. № 4. С. 62-73.
Бахтизин Р.Н., Зарипов Р.М., Коробков Г.Е., Масалимов Р.Б. Оценка влияния внутреннего давления, вызывающего дополнительный изгиб трубопровода // Записки Горного института. 2020. Т. 242. С. 160-168. DOI: 10.31897/PMI.2020.2.160
Shammazov I.A., Sidorkin D.I., Dzhemilev E.R. Research of the Dependence of the Pipeline Ends Displacement Value When Cutting Out Its Defective Section on the Elastic Stresses in the Pipe Body // IOP Conference Series: Earth and Environmental Science. 2022. Vol. 988. Iss. 2. № 022077. DOI: 10.1088/1755-1315/988/2/022077
Litvinenko V.S., Dvoynikov M.V., Trushko V.L. Elaboration of a conceptual solution for the development of the Arctic shelf from seasonally flooded coastal areas // International Journal of Mining Science and Technology. 2022. Vol. Iss. 1. P. 113-119. DOI: 10.1016/j.ijmst.2021.09.010
Манько П.О., Кочергин А.В. Диагностика трубопроводов с применением внутритрубных дефектоскопов // Вестник Луганского государственного университета имени Владимира Даля. 2021. № 9 (51). С. 35-39.
Movchan I.B., Yakovleva A.A. Approach to automation of field diagnosis data interpretation for localization of pitting in the pipeline wall // International Journal of Civil Engineering and Technology. 2019. Vol. 10. № 2. P. 1571-1581.
Глинкин Д.Ю., Межуев А.В., Юдин М.И. Перспективные направления развития ультразвуковых внутритрубных диагностических приборов // Наука и технологии трубопроводного транспорта нефти и нефтепродуктов. 2019. Т. 9. № 4. С. 434-439. DOI: 10.28999/2541-9595-2019-9-4-434-439
Базылев Д.Н., Романович В.А., Ведяков А.А. Автоматизированный метод внутритрубного ультразвукового контроля с использованием фазированной антенной решетки // Известия высших учебных заведений. Приборостроение. 2019. Т. № 9. С. 805-813. DOI: 10.17586/0021-3454-2019-62-9-805-813
Жуков А.Д., Григорьев М.В., Данилов В.Н. Исследование вопроса идентификации трещиноподобного коррозионно-механического дефекта акустическими внутритрубными инспекционными приборами // Контроль. Диагностика. 2020. № С. 56-63. DOI: 10.14489/td.2020.02.pp.056-063
Потапов А.И., Кондратьев А.В. Неразрушающий контроль многослойных сред методом годографа скорости упругих волн // Записки Горного института. 2020. Т. 243. С. 348-356. DOI: 10.31897/PMI.2020.3.348
Mitolo M., Pettinger A. Interactions Between Cathodically Protected Pipelines and Grounding Systems // IEEE Transactions on Industry Applications. 2016. Vol. 52. Iss. 5. P. 3694-3698. DOI: 10.1109/tia.2016.2582795
Болотнов А.М., Хисаметдинов Ф.З. Определение сопротивления изоляции трубопровода по результатам измерений разности потенциалов «грунт – труба» // Вестник Башкирского университета. 2017. Т. № 1. С. 20-24.
Dzhala R., Verbenets B., Dzhala V. et al. Contactless testing of insulation damages distribution of the underground pipelines // Procedia Structural Integrity. 2022. Vol. 36. P. 17-23. DOI: 10.1016/j.prostr.2021.12.077
Bhadran V., Shukla A., Karki H. Non-contact flaw detection and condition monitoring of subsurface metallic pipelines using magnetometric method // Materials Today: Proceedings. 2020. Vol. 28. Part 2. P. 860-864. DOI: 10.1016/j.matpr.2019.12.313
Bobrov A., Kuten M. Intellectual Innovations in Acoustic Emission Control in the Safety System of Pipeline Transport // Transportation Research Procedia. 2021. Vol. 54. P. 340-345. DOI: 10.1016/j.trpro.2021.02.081
Asadzadeh S., de Oliveira W.J., de Souza Filho C.R. UAV-based remote sensing for the petroleum industry and environmental monitoring: State-of-the-art and perspectives // Journal of Petroleum Science and Engineering. 2022. Vol. 208. Part D. № 109633. DOI: 10.1016/j.petrol.2021.109633
Makhutov N.A., Neganov D.A., Studenov E.P., Zorin N.E. Development of status, strength and operating life diagnostics and monitoring methods for continuously operating oil trunk pipelines // Procedia Structural Integrity. 2022. Vol. P. 283-295. DOI: 10.1016/j.prostr.2022.04.038
Григорьев Г.С, Салищев М.В., Сенчина Н.П. О применимости способа электромагнитного мониторинга гидроразрыва пласта // Записки Горного института. 2021. Т. С. 492-500. DOI: 10.31897/PMI.2021.4.2
Голубев И.А., Голубев А.В., Лаптев А.Б. Практика применения аппаратов магнитной обработки для интенсификации процессов первичной подготовки нефти // Записки Горного института. 2020. Т. 245. С. 554-560. DOI: 10.31897/PMI.2020.5.7
Mayet A.M., Alizadeh S.M., Nurgalieva K.S. et al. Extraction of Time-Domain Characteristics and Selection of Effective Features Using Correlation Analysis to Increase the Accuracy of Petroleum Fluid Monitoring Systems // Energies. 2022. Vol. 15. Iss. 6. № 1986. DOI: 10.3390/en15061986
Samimi A., Zarinabadi S., Shahbazi Kootenaei A.H. et al. Corrosion classification of pipelines in hydrocracking units (ISOMAX) by data mining // South African Journal of Chemical Engineering. 2020. Vol. 31. P. 44-50. DOI: 10.1016/j.sajce.2019.11.006
Shafeek H., Soltan H.A., Abdel-Aziz M.H. Corrosion monitoring in pipelines with a computerized system // Alexandria Engineering Journal. 2021. Vol. 60. Iss. 6. P. 5771-5778. DOI: 10.1016/j.aej.2021.04.006
Syromyatnikova A., Bolshakov A., Ivanov A. et al. The corrosion damage mechanisms of the gas pipelines in the Republic of Sakha (Yakutia) // Procedia Structural Integrity. 2019. Vol. 20. P. 259-264. DOI: 10.1016/j.prostr.2019.12.149
Lozovan V., Dzhala R., Skrynkovskyy R., Yuzevych V. Detection of specific features in the functioning of a system for the anti-corrosion protection of underground pipelines at oil and gas enterprises using neural networks // Eastern-European Journal of Enterprise Technologies. 2019. Vol. 1. Iss. 5 (97). P. 20-27. DOI: 10.15587/1729-4061.2019.154999
Krizsky V.N., Alexandrov P.N., Kovalskii A.A., Victorov S.V. Determination Transition Resistance of Cathode-Polarized Main Pipeline on Magnetometery Data // International Journal of Mathematical, Engineering and Management Sciences. 2021. Vol. 6. № P. 1729-1740. DOI: 10.33889/ijmems.2021.6.6.102
Al-Gabalawy M.A., Mostafa M.A., Hamza A.S., Hussien S.A. Modeling of the KOH-Polarization cells for mitigating the induced AC voltage in the metallic pipelines // Heliyon. 2020. Vol. 6. Iss. 3. № e03417. DOI: 10.1016/j.heliyon.2020.e03417
Dzhala R., Dzhala V., Savula R. et al. Determination of components of transient resistance of underground pipeline // Procedia Structural Integrity. 2019. Vol. P. 218-222. DOI: 10.1016/j.prostr.2019.07.044
Хисаметдинов Ф.З. Компьютерное моделирование и визуализация параметров электрического поля катодной защиты подземного трубопровода // Современные наукоемкие технологии. 2018. № С. 126-130.
Лутонин А.С., Богданова К.А. Разработка роботизированной платформы для подземного геомониторинга // Известия Тульского государственного университета. Технические науки. 2021. Вып. 12. С. 209-216. DOI: 10.24412/2071-6168-2021-12-209-217
Богданова К.А. Применение алгоритмов SLAM при построении трехмерной модели подземных горных выработок // Известия Тульского государственного университета. Технические науки. 2021. Вып. С. 134-140.
Зенцов В.Н., Болотнов А.М., Удалова Е.А. и др. Оптимизация параметров электрического поля катодной защиты от коррозии газонефтепродуктопроводов // Известия Томского политехнического университета. Инжиниринг георесурсов. 2019. Т. № 5. С. 35-43. DOI: 10.18799/24131830/2019/5/255