Определение точности нивелирных ходов по данным ГНСС/нивелирования и гравитационной модели Земли SGG-UGM-2 в некоторых типичных районах Вьетнама
- 1 — Ph.D. декан Ханойский университет природных ресурсов и окружающей среды ▪ Orcid
- 2 — декан Ханойский университет природных ресурсов и окружающей среды ▪ Orcid
Аннотация
В статье описано определение точности нивелирных ходов с помощью Глобальной навигационной спутниковой системы/нивелирования трех классов и данных гравитационной модели Земли SGG-UGM-2 в регионах Вьетнама путем расчета разницы между измеренными аномалиями высоты и моделью пар точек. Расчет производился на основе общего количества точек трех классов для четырех регионов (99 в Северо- Западном регионе, 34 в Дельте Красной реки, 130 на Центральном Нагорье и 96 в Дельте Меконга) с нивелирными ходами. В каждом регионе число пар точек составляет 189, 92, 294 и 203 соответственно. Результаты расчета точности нивелирных ходов показали, что их большинство является удовлетворительным (классы I-IV и техническое нивелирование). Определение точности нивелирных ходов полностью применимо к другим районам, если точки имеют одновременно эллипсоидальную высоту и высоту нивелирования, а также может помочь менеджерам и геодезистам в прогнозировании точности точек высоты, когда нивелирные ходы соединены.
Финансирование
Статья написана в рамках проекта TNMT.2022.562.04 Министерства природных ресурсов и окружающей среды (MONRE) Вьетнама.
Введение
Система высот – это одномерная система координат, используемая для определения метрического расстояния некоторых точек от поверхности приведения вдоль четко определенного хода, называемого высотой этой точки [1]. Соответствие поверхности приведения укажет на тип высоты: поверхность приведения геоида даст ортометрическую высоту, а поверхность приведения квазигеоида даст нормальную высоту (также известную как высота нивелирования). Поверхностью приведения является эллипсоид, который дает высоту эллипсоида.
Большинство стран в качестве национальной системы используют систему нормальных высот. Эта система представлена реперами (называемыми пунктами государственной системы высот), заложенными на местности. Нормальные высоты реперов много лет определяются по исходной поверхности – среднему уровню моря. Национальные точки высоты являются контрольными точками, которые используются во всех видах строительных работ для социально-экономического развития, безопасности и обороны каждой страны.
При составлении топографических и кадастровых карт, строительстве гражданских и промышленных сооружений, работах на транспорте, ирригации, добыче полезных ископаемых и т.д. строятся точки высот. Эти точки соединены с национальными реперами от нивелирных ходов и замкнутых нивелирных полигонов. Следовательно, если известна точность нивелирных ходов, можно прогнозировать точность высоты точек соединения с национальными точками высоты.
Определение точности нивелирных ходов для достижения класса обычно происходит в такой последовательности: измерение в поле; обработка данных измерений для расчета среднеквадратичной ошибки на один километр нивелирного хода; сравнение среднеквадратичной погрешности нивелирного хода на один километр с допустимой погрешностью измерения для нивелирования требуемого класса [2-6].
Точность нивелирных ходов определяется после измерения и обработки данных, что приводит к потере времени и денег, особенно в случае, если измерения не достигают требуемой точности. Поэтому целью данного исследования является предрасчет точности нивелирных ходов без измерений в полевых условиях. Для проведения исследования использовались гравитационная модель Земли и данные ГНСС (Глобальной навигационной спутниковой системы)/нивелирования.
Гравитационная модель Земли (EGM) представляет собой набор коэффициентов геопотенциала, используемых в разложении по сферическим гармоникам, для создания глобальной потенциальной поверхности, совпадающей со средним уровнем моря (MSL). Эта модель используется в качестве опорного геоида в мировой геодезической системе WGS. Данные гравитационной модели Земли представляются в двух форматах: в виде ряда коэффициентов сферических гармоник, определяющих модель, и в виде координаты высоты точки геоида. Точка ГНСС, имеющая высоту эллипсоида и высоту нивелирования, называется точкой ГНСС/нивелирования.
Данные ГНСС/нивелирования и гравитационная модель Земли играют важную роль в исследованиях геоида и национальных систем высот и являются исходными данными исследований.
Данные ГНСС/нивелирования используются для оценки точности глобальной гравитационной модели, например: оценки и сравнения моделей GOCE, EGM2008 в районе Средиземного моря [7], Японии [8]; оценки моделей EGM08, EIGEN-6C4, GECO в Иране [9], Турции [10]; оценки модели EGM2008 [11]; сравнения моделей XGM2019e с XGM2016, EIGEN-6C4, EGM2008 [12]; сравнения моделей EGM2008 и EGM96 в Ираке [13]; оценки моделей EGM2008, EIGEN-6C4, XGM2019e_2159 в Корее [14]; сравнения модели EIGEN-6C4 с EGM2008 в Европе, США, Канаде, Бразилии, Японии, Чехии и Словакии [15]; оценки точности моделей EGM2008, EIGEN-6C4, GECO и SGG-UGM-1 в Кении [16]; оценки моделей EGM2008, EIGEN6C4 и GECO в Эгейском регионе [17]; оценки моделей EGM96, EGM84 и EGM2008 в Ираке [18]; сравнения моделей EGM96 и EGM2008 в Ираке [19]; сравнения моделей OUS-91A, EGM96 и EGM2008 в Египте [20]; оценки модели EGM2008 в Бангладеш [21]. Также данные ГНСС/нивелирования используются для построения локальных моделей геоида, например в Ираке [19], Турции [22], Эвбориарии, Бенин-Сити (Нигерия) [23].
Данные ГНСС/нивелирования применялись для коррекции глобальной гравитационной модели и построения локальной модели геоида: модель EGM2008 и данные ГНСС/нивелирования для построения локальной модели геоида в Индонезии [24], Нигерии [25], Вьетнаме [26], Турции [27], Египте [28], Китае [29], США [30]; модель EIGEN6C4, данные нивелирования, ГНСС – для построения локальной модели геоида в Уганде [31].
Данные ГНСС/нивелирования и глобальная гравитационная модель использовались для построения системы высот в Италии [32], данные ГНСС/нивелирования и модель EGM2008 – в Палестине [33]; ГНСС/нивелирование применялось вместе с данными GOCE для оценки системы отсчета высоты в Канаде [34].
Для построения локальной модели геоида использовались данные ГНСС/нивелирования, глобальная гравитационная модель и другие данные: ГНСС/нивелирование вместе с данными EGM2008, цифровой земной моделью – для определения модели геоида в Мексике [35]; ГНСС/нивелирование вместе с гравиметрическими данными EIGEN-6C4 – для построения модели геоида в Катаре [36]; ГНСС/нивелирование вместе с данными GOCE – для построения моделей геоида в штате Сан-Паулу (Бразилия) [37]; ГНСС/нивелирование вместе с модельными данными XGM2019e_2159, цифровой земной моделью ACE2 GDEM – для построения модели геоида в Египте [28]; ГНСС/нивелирование вместе с модельными, гравиметрическими, топографическими данными высокого разрешения, батиметрическими данными – для построения модели геоида во Вьетнаме [38].
Данные ГНСС/нивелирования и гравитационная модель Земли являются незаменимыми при изучении вопросов, связанных с высотами в странах. Это источник исходных данных для подтверждения оценки точности глобальной гравитационной модели, построения национальной системы высот и локальной модели геоида.
В данном исследовании, основанном на данных ГНСС/нивелирования и гравитационной модели Земли, логично представлена теоретическая основа для определения точности нивелирных ходов. На основании собранных данных в качестве экспериментальных выбраны участки на территории Вьетнама.
Теоретическая основа
Отношение между высотой эллипсоида h и нормальной высотой H представлено формулой
где ζiГНСС/нивилирование – аномалия высоты точки i.
Значение аномалии высоты также может быть определено на основании гравитационной модели Земли.
Для определения точности нивелирного хода, соединяющего национальные точки ГНСС/нивелирования, сравниваются значения аномалии высоты при определении по данным ГНСС/нивелирования с соответствующими данными, взятыми из гравитационной модели Земли.
Предлагаемая ζiмодель является аномалией высоты точки i, извлеченной из гравитационной модели Земли. Формула для расчета аномалии высоты точки i записывается следующим образом:
Расчет среднего значения отклонения аномалии высоты может быть выполнен по формуле
где n – номера точек.
Отклонение пары точек i и j (рис.1) рассчитывается по формуле
Объединив формулы (2) и (3), получаем выражение
Принимая формулы
получаем уравнение
Вес уравнения (6) рассчитывается по формуле
где D – расстояние между точками i и j, км.
Среднеквадратичная ошибка разности аномалий высот на один километр рассчитывается по формуле
где q – число пар точек, используемых для расчета.
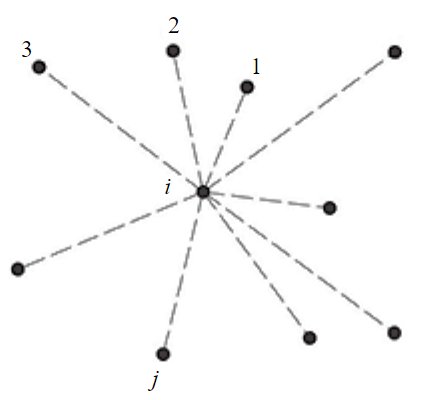
Рис.1. Пары точек
Уточнены национальный стандарт для сетей высот зданий, допустимая погрешность нивелирного хода, замкнутого нивелирного хода по классам. Для горных районов Вьетнама допустимая погрешность для замкнутого нивелирного хода I, II, III, IV классов составляет 3√L, 5√L, 12√L, 25√L соответственно (L, мм), на равнинах эти ошибки равны 2√L, 4√L, 10√L, 20√L соответственно; для технического нивелирования погрешность составляет 50√L (L в км).
Вьетнам – страна, в которой преобладают невысокие холмы и горы, при этом равнины составляют около четверти территории. По топографии и экономическому развитию Вьетнам разделяется на следующие регионы:
- Северо-Западный регион – местность с множеством высоких горных хребтов;
- Северо-Восточный регион – невысокие холмы;
- Дельта Красной реки – относительно равнинная местность, является экономическим центром Северного региона Вьетнама;
- Северная часть Центрального побережья – смешанный рельеф гор, холмов и равнин;
- Южная часть Центрального побережья – невысокие холмы и равнины;
- Район Нагорья – разнообразный рельеф включает высокие горы, плоскогорья и обширные равнины;
- Юго-Восточный регион – удаленные от моря районы и невысокие холмы;
- Юго-Западный регион или Дельта Меконга – относительно плоский рельеф, довольно низкий по сравнению с уровнем моря, часто подвержен воздействию приливов и отливов.
В соответствии с национальным стандартом для сети высот зданий на участках с различной топографией погрешность замкнутых нивелирных ходов различается в зависимости от класса. Поэтому для исследований выбраны районы, имеющие типичный для Вьетнама рельеф: Северо-Западный регион, Дельта Красной реки, Центральное Нагорье, Дельта Меконга. Источники, используемые в анализе, включают данные ГНСС/нивелирования и гравитационной модели Земли.
Данные ГНСС/нивелирования
Число точек национального ГНСС/нивелирования в каждом экспериментальном районе указано в табл.1. Нивелирование и геодезические высоты точек ГНСС/нивелирования подробно описаны в табл.2.
Таблица 1
Точки ГНСС/нивелирования
|
Регион |
Число точек ГНСС/нивелирования |
Итого |
||
|
Класс I |
Класс II |
Класс III |
||
|
Северо-Западный |
35 |
16 |
48 |
99 |
|
Дельта Красной реки |
20 |
11 |
3 |
34 |
|
Центральное Нагорье |
24 |
26 |
80 |
130 |
|
Дельта Меконга |
13 |
52 |
31 |
96 |
Таблица 2
Данные по точкам ГНСС/нивелирования
|
Номер точки |
Индекс точки |
B0 |
L0 |
h, м |
H, м |
|
1 |
I(BMT-APD)12 |
12,28926 |
107,59477 |
907,6780 |
907,9755 |
|
2 |
I(BMT-APD)1-2 |
12,65835 |
108,02837 |
431,3888 |
431,2042 |
|
3 |
I(BMT-APD)16 |
12,10935 |
107,65618 |
833,2335 |
832,9730 |
|
4 |
I(BMT-APD)22 |
11,99578 |
107,51564 |
732,3017 |
732,6708 |
|
5 |
I(BMT-APD)25 |
11,93166 |
107,42908 |
575,1619 |
576,0473 |
|
6 |
I(BMT-APD)3 |
12,58108 |
107,84340 |
358,1393 |
358,6506 |
|
7 |
I(BMT-APD)6 |
12,49414 |
107,74019 |
580,5556 |
581,0788 |
|
8 |
I(BMT-NH)11-1 |
12,80411 |
108,54048 |
468,5150 |
466,5640 |
|
9 |
I(BMT-NH)17-1 |
12,73304 |
108,75417 |
423,7629 |
420,9371 |
|
10 |
I(BMT-NH)22 |
12,58583 |
108,85847 |
561,2232 |
557,7819 |
|
… |
… |
… |
… |
… |
… |
|
351 |
III(TT-GR)4 |
9,95520 |
105,36885 |
–5,6633 |
0,9933 |
|
352 |
III(TT-HN)2 |
10,92092 |
105,42574 |
–4,3237 |
4,1669 |
|
353 |
III(TT-TS)1 |
10,25559 |
105,16435 |
–5,4807 |
2,6149 |
|
354 |
III(TV-LS)9 |
9,71773 |
106,42700 |
–0,1141 |
2,0210 |
|
355 |
III(TY-VD)9 |
9,22404 |
104,81945 |
–6,3808 |
0,4914 |
|
356 |
III(UM-HDB)7 |
10,52037 |
104,70823 |
–8,4336 |
2,0185 |
|
357 |
III(VL-MC)7 |
10,23367 |
106,18661 |
–2,0257 |
1,8265 |
|
358 |
III(VT-PS)5 |
9,37355 |
105,39224 |
–4,1265 |
1,1779 |
|
359 |
III(VT-VC)7 |
9,29983 |
105,93297 |
–1,2964 |
1,4918 |
Данные гравитационной модели Земли
Гравитационная модель Земли SGG-UGM-2 – модель, опубликованная в 2020 г. Доступ к данным этой модели можно получить на сайте Международного центра глобальных моделей Земли (ICGEM) (http://icgem.gfz-potsdam. de/tom). Данные об аномалиях высот точек ГНСС/нивелирования, полученные из гравитационной модели Земли, приведены в табл.3.
Таблица 3
Данные об аномалиях высот точек ГНСС/нивелирования из гравитационной модели Земли
|
Номер точки |
Индекс точки |
м |
Номер точки |
Индекс точки |
м |
|
1 |
I(BMT-APD)12 |
–0,6568 |
… |
… |
… |
|
2 |
I(BMT-APD)1-2 |
–0,4138 |
351 |
III(TT-GR)4 |
–6,9711 |
|
3 |
I(BMT-APD)16 |
–0,0710 |
352 |
III(TT-HN)2 |
–9,1764 |
|
4 |
I(BMT-APD)22 |
–0,6639 |
353 |
III(TT-TS)1 |
–8,7063 |
|
5 |
I(BMT-APD)25 |
–1,1798 |
354 |
III(TV-LS)9 |
–2,4782 |
|
6 |
I(BMT-APD)3 |
–1,0340 |
355 |
III(TY-VD)9 |
–7,1055 |
|
7 |
I(BMT-APD)6 |
–1,0081 |
356 |
III(UM-HDB)7 |
–11,1486 |
|
8 |
I(BMT-NH)11-1 |
1,3586 |
357 |
III(VL-MC)7 |
–4,1515 |
|
9 |
I(BMT-NH)17-1 |
2,3220 |
358 |
III(VT-PS)5 |
–5,4536 |
|
10 |
I(BMT-NH)22 |
3,0755 |
359 |
III(VT-VC)7 |
–3,1043 |
Результаты и обсуждение
Этапы определения точности нивелирных ходов:
- Расчет аномалии высот по данным измерений ГНСС/нивелирования ζiГНСС/нивилирование (формула (2).
- Расчет отклонения аномалии высоты между измеренной аномалией высоты и модели Δζi; среднее значение аномалии высоты ζiсреднее рассчитывается по формуле (3).
- Расчет отклонения аномалий высот пар точек Δζij (формула (5).
- Вычисление веса нивелирного хода Рij(формула (8).
- Расчет среднеквадратичной ошибки разности аномалий высот на один километр хода mкм – формула (9) – для нивелирного хода четырех регионов.
- Расчет допустимой ошибки для каждой трассы нивелирования mдопустимая.
- Сравнение среднеквадратичной ошибки разности аномалий высот на один километр каждого нивелирного хода с допустимой ошибкой.
Результаты расчетов на этапах 1 и 2 представлены в табл.4 и рис.2.
Таблица 4
Аномалии высот по данным измерений ГНСС/нивелирования и их отклонение от модельного значения
|
Номер точки |
Индекс точки |
ζiГНСС/нивилирование, м |
Δζi, м |
Номер точки |
Индекс точки |
ζiГНСС/нивилирование, м |
Δζi, м |
|
1 |
I(BMT-APD)12 |
–0,2975 |
0,3593 |
… |
… |
… |
… |
|
2 |
I(BMT-APD)1-2 |
0,1846 |
0,5984 |
351 |
III(TT-GR)4 |
–6,6566 |
0,3145 |
|
3 |
I(BMT-APD)16 |
0,2605 |
0,3315 |
352 |
III(TT-HN)2 |
–8,4906 |
0,6858 |
|
4 |
I(BMT-APD)22 |
–0,3691 |
0,2948 |
353 |
III(TT-TS)1 |
–8,0956 |
0,6107 |
|
5 |
I(BMT-APD)25 |
–0,8854 |
0,2944 |
354 |
III(TV-LS)9 |
–2,1351 |
0,3431 |
|
6 |
I(BMT-APD)3 |
–0,5113 |
0,5227 |
355 |
III(TY-VD)9 |
–6,8722 |
0,2333 |
|
7 |
I(BMT-APD)6 |
–0,5232 |
0,4849 |
356 |
III(UM-HDB)7 |
–10,4521 |
0,6965 |
|
8 |
I(BMT-NH)11-1 |
1,9510 |
0,5924 |
357 |
III(VL-MC)7 |
–3,8522 |
0,2993 |
|
9 |
I(BMT-NH)17-1 |
2,8258 |
0,5038 |
358 |
III(VT-PS)5 |
–5,3044 |
0,1492 |
|
10 |
I(BMT-NH)22 |
3,4413 |
0,3658 |
359 |
III(VT-VC)7 |
–2,7882 |
0,3161 |
Из рис.2 видно, что рельеф в четырех регионах более высокий, чем по данным модели SGG-UGM-2. Среднее значение отклонения аномалии высот точек ГНСС/нивелирования между измерениями и моделью составляет в Северо-Западном регионе 0,4249 м, в Дельте Красной реки 0,6369 м, на Центральном Нагорье 0,4638 м и Дельте Меконга 0,3588 м.
Результаты расчетов на этапах 3 и 4. По точкам ГНСС/нивелирования в четырех регионах проложены нивелирные ходы на основании пар точек, причем число ходов составляет в Северо-Западном регионе 189, Дельте Красной реки 92, на Центральном Нагорье 294 и в Дельте Меконга 203. Измеренные значения аномалий высот и модели ходов ГНСС/нивелирования приведены в табл.5.
Таблица 5
Отклонение аномалий высот для пар точек в национальной системе ГНСС/нивелирования
|
Номер точки |
Исходная точка |
Конечная точка |
D, км |
ζijГНСС/нивилирование, м |
Δζijмодель м |
Δζij ,м |
Pij |
|
1 |
I(BMT-APD)12 |
I(BMT-APD)16 |
21,0 |
–0,5580 |
–0,5858 |
0,0278 |
0,048 |
|
2 |
I(BMT-APD)12 |
III(DBS-DL)3 |
23,4 |
0,3530 |
0,1683 |
0,1847 |
0,043 |
|
3 |
I(BMT-APD)12 |
III(QS-DN)2 |
29,8 |
–1,1846 |
–1,2386 |
0,0540 |
0,034 |
|
4 |
I(BMT-APD)12 |
III(BDS-QP)5 |
33,0 |
–0,7274 |
–0,4316 |
–0,2958 |
0,030 |
|
5 |
I(BMT-APD)22 |
I(BMT-APD)25 |
11,8 |
0,5163 |
0,5159 |
0,0004 |
0,085 |
|
6 |
I(BMT-APD)22 |
I(BMT-APD)16 |
19,8 |
–0,6296 |
–0,5930 |
–0,0366 |
0,050 |
|
7 |
I(BMT-APD)25 |
I(BMT-APD)30 |
24,0 |
0,9462 |
0,9868 |
–0,0406 |
0,042 |
|
8 |
I(BMT-APD)25 |
III(BGM-MH)3 |
32,7 |
1,6841 |
1,8078 |
–0,1237 |
0,031 |
|
9 |
I(BMT-APD)3 |
I(BMT-APD)6 |
14,8 |
0,0119 |
–0,0259 |
0,0378 |
0,068 |
|
10 |
I(BMT-APD)3 |
III(BDS-QP)5 |
21,3 |
–0,9412 |
–0,8088 |
–0,1324 |
0,047 |
|
… |
… |
… |
… |
… |
|
… |
… |
|
767 |
III(TT-HN)2 |
II(HN-AB)7 |
23,7 |
–0,7255 |
–1,0619 |
0,3364 |
0,042 |
|
768 |
III(TT-TS)1 |
II(CD-VC)8 |
32,3 |
–0,1642 |
–0,5622 |
0,3980 |
0,031 |
|
769 |
III(UM-HDB)7 |
III(OD-CN)1 |
26,1 |
–0,7561 |
–0,6581 |
–0,0980 |
0,038 |
|
770 |
III(VL-MC)7 |
II(TL-TV)5-1 |
17,5 |
–0,6959 |
–0,6593 |
–0,0366 |
0,057 |
|
771 |
III(VL-MC)7 |
II(MT-TV)6-1 |
17,6 |
–0,1647 |
–0,1954 |
0,0307 |
0,057 |
|
772 |
III(VL-MC)7 |
III(LH-TH)1 |
21,6 |
0,3888 |
0,4602 |
–0,0714 |
0,046 |
|
773 |
III(VL-MC)7 |
I(VL-HT)273A |
23,1 |
–0,3478 |
–0,3374 |
–0,0104 |
0,043 |
|
774 |
III(VL-MC)7 |
II(TX-TL)25 |
24,9 |
1,1117 |
1,1544 |
–0,0427 |
0,040 |
|
775 |
III(VL-MC)7 |
I(VL-HT)284A |
29,2 |
–1,1320 |
–0,9975 |
–0,1345 |
0,034 |
|
776 |
III(VT-PS)5 |
II(SC-PL)34 |
20,7 |
0,9892 |
0,9625 |
0,0267 |
0,048 |
|
777 |
III(VT-PS)5 |
II(SC-PL)15 |
21,9 |
0,6785 |
0,5949 |
0,0836 |
0,046 |
|
778 |
III(VT-VC)7 |
II(ST-PL)2 |
27,5 |
–0,7561 |
–0,6581 |
–0,0980 |
0,036 |
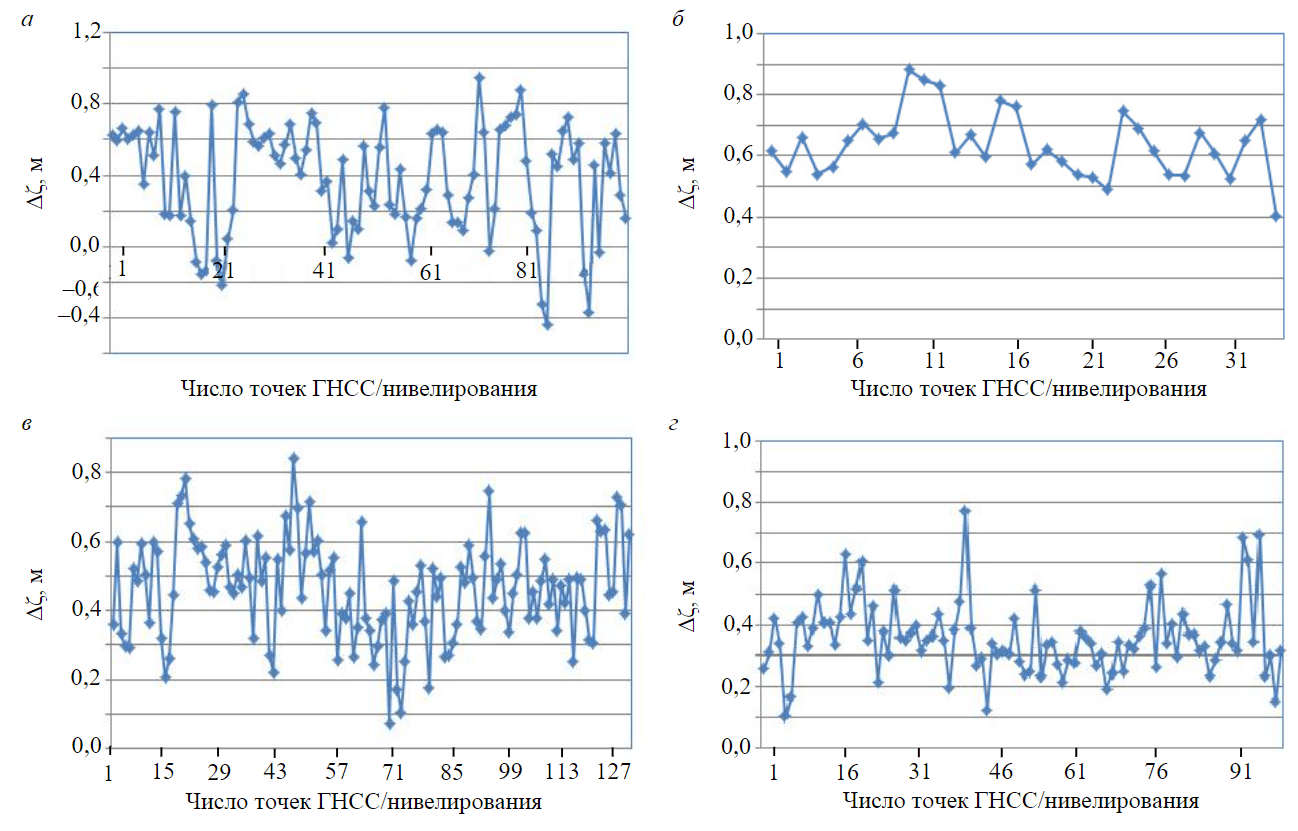
Рис.2. Аномалии высот модели SGG-UGM-2 и системы ГНСС/нивелирования: а – Северо-Западный регион; б – Дельта Красной реки; в – Центральное Нагорье; г – Дельта Меконга
Результаты расчетов этапов 5-7. Среднеквадратичная ошибка разности аномалий высот на один километр в четырех регионах рассчитывается по формуле (9):
Для определения точности каждого нивелирного хода необходимо определить два типа ошибок:
- среднеквадратичная ошибка разности аномалий высот на один километр показывает точность нивелирного хода, которая рассчитывается по формуле (9); в случае, если имеется только один нивелирный ход, q = 1, P = 1, и среднеквадратичная ошибка разности аномалий высот на один километр будет также рассчитываться по формуле ;
- допустимая ошибка также рассчитывается для каждого нивелирного хода на основании рельефа местности; если местность равнинная, значение L = 1,1D (расстоянию между двумя точками); если местность гористая, значение L = 1,3D.
Значение ошибки для каждого нивелирного хода показано в табл.6.
Таблица 6
Погрешность трассы нивелирования
|
Номер точки |
Исходная точка |
Конечная точка |
|mкм|, мм |
Абсолютное значение допустимой ошибки, мм |
Достигнутый класс трассы нивелирования |
||||
|
Класс I |
Класс II |
Класс III |
Класс IV |
Техническое нивелирование |
|||||
|
1 |
I(BMT-APD)12 |
I(BMT-APD)16 |
27,8 |
15,7 |
26,1 |
62,7 |
130,6 |
313,6 |
Класс III |
|
2 |
I(BMT-APD)12 |
III(DBS-DL)3 |
184,7 |
16,5 |
27,6 |
66,2 |
137,9 |
330,9 |
Технический |
|
3 |
I(BMT-APD)12 |
III(QS-DN)2 |
54,0 |
18,7 |
31,1 |
74,7 |
155,6 |
373,3 |
Класс III |
|
4 |
I(BMT-APD)12 |
III(BDS-QP)5 |
295,8 |
19,7 |
32,8 |
78,7 |
163,9 |
393,3 |
Технический |
|
5 |
I(BMT-APD)22 |
I(BMT-APD)25 |
0,4 |
11,8 |
19,6 |
47,0 |
97,9 |
235,0 |
Класс I |
|
6 |
I(BMT-APD)22 |
I(BMT-APD)16 |
36,6 |
15,2 |
25,4 |
60,9 |
126,9 |
304,5 |
Класс III |
|
7 |
I(BMT-APD)25 |
I(BMT-APD)30 |
40,6 |
16,8 |
27,9 |
67,0 |
139,6 |
335,1 |
Класс III |
|
8 |
I(BMT-APD)25 |
III(BGM-MH)3 |
123,7 |
19,6 |
32,6 |
78,3 |
163,0 |
391,3 |
Класс IV |
|
9 |
I(BMT-APD)3 |
I(BMT-APD)6 |
37,8 |
13,2 |
21,9 |
52,6 |
109,6 |
263,1 |
Класс III |
|
10 |
I(BMT-APD)3 |
III(BDS-QP)5 |
132,4 |
15,8 |
26,3 |
63,1 |
131,5 |
315,6 |
Технический |
|
… |
… |
… |
|
|
|
… |
… |
… |
… |
|
767 |
III(TT-HN)2 |
II(HN-AB)7 |
336,4 |
10,2 |
20,4 |
51,1 |
102,1 |
255,4 |
Неудовлетворительная |
|
768 |
III(TT-TS)1 |
II(CD-VC)8 |
398,0 |
11,9 |
23,8 |
59,6 |
119,2 |
298,0 |
Неудовлетворительная |
|
769 |
III(UM-HDB)7 |
III(OD-CN)1 |
98,0 |
10,7 |
21,4 |
53,6 |
107,2 |
268,1 |
Класс IV |
|
770 |
III(VL-MC)7 |
II(TL-TV)5-1 |
36,6 |
8,8 |
17,6 |
43,9 |
87,8 |
219,5 |
Класс III |
|
771 |
III(VL-MC)7 |
II(MT-TV)6-1 |
30,7 |
8,8 |
17,6 |
44,0 |
87,9 |
219,9 |
Класс III |
|
772 |
III(VL-MC)7 |
III(LH-TH)1 |
71,4 |
9,8 |
19,5 |
48,8 |
97,6 |
243,9 |
Класс IV |
|
773 |
III(VL-MC)7 |
I(VL-HT)273A |
10,4 |
10,1 |
20,2 |
50,4 |
100,9 |
252,1 |
Класс II |
|
774 |
III(VL-MC)7 |
II(TX-TL)25 |
77,8 |
10,5 |
20,9 |
52,4 |
104,7 |
261,8 |
Класс IV |
|
775 |
III(VL-MC)7 |
I(VL-HT)284A |
42,7 |
11,3 |
22,7 |
56,6 |
113,3 |
283,2 |
Класс III |
|
776 |
III(VT-PS)5 |
II(SC-PL)34 |
134,5 |
9,5 |
19,1 |
47,7 |
95,4 |
238,5 |
Технический |
|
777 |
III(VT-PS)5 |
II(SC-PL)15 |
26,7 |
9,8 |
19,6 |
49,1 |
98,2 |
245,4 |
Класс III |
|
778 |
III(VT-VC)7 |
II(ST-PL)2 |
83,6 |
11,0 |
22,0 |
55,0 |
110,0 |
274,9 |
Класс IV |
Сумма нивелирных ходов, соответствующих классам для каждого региона в табл.6, представлена в табл.7. Число нивелирных ходов каждого класса в четырех регионах рассчитывается делением числа нивелирных ходов каждого класса на их общее число в каждом регионе.
Таблица 7
Достигнутые классы и процент точности нивелирных ходов
|
Регион |
Достигнутые классы нивелирных ходов |
Точность, % |
|||||||||||
|
Удовлетворительная |
Неудовлетворительная |
||||||||||||
|
Класс Ι |
Класс ΙΙ |
Класс ΙΙΙ |
Класс ΙV |
Инженерное нивелирование |
Неудовлетворительное |
Итого |
Класс Ι |
Класс ΙΙ |
Класс ΙΙΙ |
Класс ΙV |
Техническое нивелирование |
||
|
Северо-Западный |
13 |
7 |
25 |
45 |
68 |
31 |
189 |
6,9 |
3,7 |
13,2 |
23,8 |
36,0 |
16,4 |
|
Дельта Красное реки |
9 |
7 |
15 |
28 |
30 |
3 |
92 |
9,8 |
7,6 |
16,3 |
30,4 |
32,6 |
3,3 |
|
Центральное Нагорье |
31 |
15 |
62 |
97 |
85 |
4 |
294 |
10,5 |
5,1 |
21,1 |
33,0 |
28,9 |
1,4 |
|
Дельта Меконга |
16 |
14 |
35 |
51 |
67 |
20 |
203 |
7,9 |
6,9 |
17,2 |
25,1 |
33,0 |
9,9 |
У большинства нивелирных ходов в четырех регионах процент точности удовлетворительный (классы I-IV и техническое нивелирование). Наивысший класс, который можно получить, – это класс I.
Заключение
Результаты определения точности нивелирных ходов по данным ГНСС/нивели-рования и гравитационной модели Земли SGG-UGM-2 в четырех регионах Вьетнама – Северо-Западный, Дельта Красной реки, Центральное Нагорье, Дельта Меконга – путем расчета разницы между измеренными аномалиями высот и моделью пар точек и нивелирных ходов, соединенных с парами точек в каждом регионе, показали удовлетворительный процент точности нивелирных ходов.
Определение точности нивелирных ходов позволяет не тратить время и деньги, поскольку отсутствует необходимость измерения в полевых условиях. Определение точности нивелирных ходов вполне применимо и к другим районам, если точки имеют одновременно и геодезическую, и нивелирную высоты.
При реализации проекта по данным результатам менеджеры и геодезисты могут предварительно рассчитывать точность высотных отметок при соединении нивелирных ходов.
Литература
- Featherstone W.E., Kuhn M. Height systems and vertical datums: A review in the Australian context // Journal of Spatial Sciences. 2006. Vol. 51. Iss. 1. P. 21-41. DOI: 10.1080/14498596.2006.9635062
- El-Ashmawy K.L.A. Accuracy, time cost and terrain independence comparisons of levelling techniques // Geodesy and Cartography. 2014. Vol. 40. Iss. 3. P. 133-141. DOI: 10.3846/20296991.2014.962727
- Karila K., Karjalainen M., Hyyppä J. et al. A Comparison of Precise Leveling and Persistent Scatterer SAR Interferometry for Building Subsidence Rate Measurement // ISPRS International Journal of Geo-Information. 2013. Vol. 2. Iss. 3. P. 797-816. DOI: 10.3390/ijgi2030797
- Kubodera T., Okazawa H., Hosokawa Y. et al. Effects of Surveying Methods between GNSS and Direct Leveling on Elevation Values over Long Distance in Mountainous Area // International Journal of Environmental and Rural Development. 2016. Vol. 7. Iss. 1. P. 62-69. DOI: 10.32115/ijerd.7.1_62
- Perij S., Pokotylo I., Korliatovych T. Investigation of accuracy of methods of trigonometric levelling during the transmission of elevations over water surfaces // Geodesy, Cartography, and Aerial Photography. 2017. Vol. 85. P. 18-26. DOI: 10.23939/istcgcap2017.01.018
- Ding Liang Yang, Jin Gui Zou. Precise levelling in crossing river over 5 km using total station and GNSS // Scientific Reports. 2021. Vol. 11. № 7492. DOI: 10.1038/s41598-021-86929-1
- Carrion D., Vergos G., Albertella A. et al. Assessing the GOCE models accuracy in the Mediterranean area // Newton’s Bulletin. 2015. Vol. 5. P. 63-82.
- Odera P.A., Fukuda Y. Evaluation of GOCE-based global gravity feld models over Japan after the full mission using free-air gravity anomalies and geoid undulations // Earth, Planets and Space. 2017. Vol. 69. № 135. DOI: 10.1186/s40623-017-0716-1
- Foroughi I., Afrasteh Y., Ramouz S., Safari A. Local evaluation of Earth gravitational models, case study: Iran // Geodesy and Cartography. 2017. Vol. 43. Iss. 1. P. 1-13. DOI: 10.3846/20296991.2017.1299839
- Yılmaz M., Turgut B., Güllü M., Yılmaz I. The Evaluation of High-Degree Geopotential Models for Regional Geoid Determination in Turkey // Afyon Kocatepe University Journal of Science and Engineering. 2017. Vol. 17. № 015501. P. 147-153. DOI: 10.5578/fmbd.50706
- Pavlis N.K., Holmes S.A., Kenyon S.C., Factor J.K. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008) // Journal of Geophysical Research: Solid Earth. 2012. Vol. 117. № B04406. P. 1-38. DOI: 10.1029/2011JB008916
- Zingerle P., Pail R., Gruber T., Oikonomidou X. The combined global gravity field model XGM2019e // Journal of Geodesy. 2020. Vol. 94. № 66. DOI: 10.1007/s00190-020-01398-0
- Aljanbi A.J.A., Dibs H., Alyasery B.H. Interpolation and Statistical Analysis for Evaluation of Global Earth Gravity Models Based on GPS and Orthometric Heights in the Middle of Iraq // Iraqi Journal of Science. 2020. Vol. 61. № 7. P. 1823-1830. DOI: 10.24996/ijs.2020.61.7.31
- Lee J., Kwon J.H. Precision Evaluation of Recent Global Geopotential Models based on GNSS/Leveling Data on Unified Control Points // Journal of the Korean Society of Surveying, Geodesy, Photogrammetry and Cartography. 2020. Vol. 38. № 2. P. 153-163. DOI: 10.7848/ksgpc.2020.38.2.153
- Kostelecký J., Klokočník J., Bucha B. et al. Evaluation of gravity field model EIGEN-6C4 by means of various functions of gravity potential, and by GNSS/leveling // Geoinformatics FCE CTU. 2015. Vol. 14. № 1. P. 7-28. DOI: 10.14311/gi.14.1.1
- Odera P.A. Evaluation of the recent high-degree combined global gravity-field models for geoid modelling over Kenya // Geodesy and Cartography. 2020. Vol. 46. Iss. 2. P. 48-54. DOI: 10.3846/gac.2020.10453
- Yilmaz M., Turgut B., Gullu M., Yilmaz I. Evaluation of recent global geopotential models by GNSS/levelling data: Internal Aegean region // International Journal of Engineering and Geosciences (IJEG). 2016. Vol. 1. Iss. 1. P. 18-23. DOI: 10.26833/ijeg.285221
- Saray N.S., Ghazal N.K. Evaluation of Global Gravitational Models Based on DGPS/leveling Data over Baghdad University (IRAQ) // Journal of Physics: Conference Series. 2021. Vol. 1804. № 012044. DOI: 10.1088/1742-6596/1804/1/012044
- Abdulrahman F.H. Determination of the local geoid model in Duhok Region, University of Duhok Campus as a Case study // Ain Shams Engineering Journal. 2021. Vol. 12. Iss. 2. P. 1293-1304. DOI: 10.1016/j.asej.2020.10.004
- Al-Karargy E.M., Doma M.I., Dawod G.M. Towards an Accurate Definition of the Local Geoid Model in Egypt using GPS/Leveling Data: A Case Study at Rosetta Zone // International Journal of Innovative Science and Modern Engineering (IJISME). 2014. Vol. 2. Iss. 11. P. 10-15.
- Sikder M.A.A., Falin Wu, Ahmed W.A. et al. Assessment of Orthometric Height Derived from Levelling, GNSS and EGM2008 Geoid Model in Bangladesh // 15th IEEE International Conference on Signal Processing (ICSP), 6-9 December 2020, Beijing, China. IEEE, 2020. P. 689-694. DOI: 10.1109/ICSP48669.2020.9321048
- Albayrak M., Özlüdemir M.T., Aref M.M., Halicioglu K. Determination of Istanbul geoid using GNSS/levelling and valley cross levelling data // Geodesy and Geodynamics. 2020. Vol. 11. Iss. 3. P. 163-173. DOI: 10.1016/j.geog.2020.01.003
- Eteje S.O., Ono M.N., Oduyebo O.F. Practical local geoid model determination for mean sea level heights of surveys and stable building projects // IOSR Journal of Environmental Science, Toxicology and Food Technology. 2018. Vol. 12. Iss. 6. P. 30-37. DOI: 10.5281/zenodo.2525661
- Heliani L.S. Evaluation of global geopotential model and its application on local geoid modelling of Java Island, Indonesia // AIP Conference Proceedings. 2016. Vol. 1755. Iss. 1. № 100005. DOI: 10.1063/1.4958534
- Oluyori P.D., Ono M.N., Eteje S.O. Computations of Geoid Undulation from Comparison of GNSS/Levelling with EGM 2008 for Geodetic Applications // International Journal of Scientific and Research Publications. 2018. Vol. 8. Iss. 10. P. 235-241. DOI: 10.29322/IJSRP.8.10.2018
- Thanh Son Tran, Mustafin M.G., Kuzin A.A. Creating a Local Quasigeoid Model for the Territory of Vietnam Using the Global Model EGM2008 // Proceedings of the International Symposium «Engineering and Earth Sciences: Applied and Fundamental Research» (ISEES 2019), 10-13 June 2019, Grozny, Russia. Amsterdam: Atlantis Press, 2019. Vol. 1. P. 603-608. DOI: 10.2991/isees-19.2019.119
- Soycan M. Improving EGM2008 by GPS and leveling data at local scale // Boletim de Ciências Geodésicas. 2014. Vol. 20. Iss. 1. P. 3-18. DOI: 10.1590/S1982-21702014000100001
- Al-Karargy E.M., Dawod G.M. Optimum combinations of GGM and GDEM models for precise national geoid modeling // Proceedings of Engineering and Technology Innovation. 2021. Vol. 18. P. 15-24. DOI: 10.46604/peti.2021.6452
- Wei Liang, Roland Pail, Xinyu Xu, Jiancheng Li. A new method of improving global geopotential models regionally using GNSS/levelling data // Geophysical Journal International. 2020. Vol. 221. Iss. 1. P. 542-549. DOI: 10.1093/gji/ggaa047
- Mosayebzadeh M., Ardalan A.A., Karimi R. Regional improvement of global geopotential models using GPS/Leveling data // Studia Geophysica et Geodaetica. 2019. Vol. 63. P. 169-190. DOI: 10.1007/s11200-017-1084-9
- Kyamulesire B., Oluyori P.D., Eteje S.O. Comparative analysis of three plane geometric geoid surfaces for orthometric height modelling in Kampala, Uganda // FUDMA Journal of Sciences (FJS). 2020. Vol. 4. № 3. P. 48-51. DOI: 10.33003/fjs-2020-0403-255
- Barzaghi R., Carrion D., Reguzzoni M., Venuti G. A Feasibility Study on the Unification of the Italian Height Systems Using GNSS-Leveling Data and Global Satellite Gravity Models / IAG 150 Years. International Association of Geodesy Symposia. Cham: Springer, 2015. Vol. 143. P. 281-288. DOI: 10.1007/1345_2015_35
- Younis G. The Integration of GNSS/Leveling Data with Global Geopotential Models to Define the Height Reference System of Palestine // Arabian Journal for Science and Engineering. 2018. Vol. 43. № 7. P. 3639-3645. DOI: 10.1007/s13369-017-2912-5
- Hayden T., Amjadiparvar B., Rangelova E., Sideris M.G. Estimating Canadian vertical datum offsets using GNSS/levelling benchmark information and GOCE global geopotential models // Journal of Geodetic Science. 2012. Vol. 2. Iss. 4. P. 257-269. DOI: 10.2478/v10156-012-0008-4
- Alcantar-Elizondo N., Garcia-Lopez R.V., Torres-Carillo X.G., Vazquez-Becerra G.E. Combining Global Geopotential Models, Digital Elevation Models, and GNSS/Leveling for Precise Local Geoid Determination in Some Mexico Urban Areas: Case Study // ISPRS International Journal of Geo-Information. 2021. Vol. 10. Iss. 12. № 819. DOI: 10.3390/ijgi10120819
- Bos M., Fernandes R., Al-Marri M. et al. The New Gravimetric Geoid Model of Qatar: QG2020 // FIG e-Working Week 2021, 21-25 June 2021, Netherlands.
- Guimarães G.D.N., Blitzkow D., Barzaghi R., Matos A.C.O.C. The computation of the geoid model in the state of São Paulo using two methodologies and GOCE models // Boletim de Ciências Geodésicas. 2014. Vol. 20. № 1. P. 183-203. DOI: 10.1590/S1982-21702014000100012
- Vu D.T., Bruinsma S., Bonvalot S. A high-resolution gravimetric quasigeoid model for Vietnam // Earth, Planets and Space. 2019. Vol. 71. № 65. DOI: 10.1186/s40623-019-1045-3
