Исследование вероятностных моделей для прогнозирования  эффективности технологии пропантного гидравлического разрыва пласта

В. И. Галкин; А. Н. Колтырин

doi:10.31897/PMI.2020.6.7

Том 246

Страницы:

650-659

Скачать том:

RUS ENG

Нефтегазовое дело

Исследование вероятностных моделей для прогнозирования эффективности технологии пропантного гидравлического разрыва пласта

Авторы:

В. И. Галкин¹

А. Н. Колтырин²

Об авторах

1 — д-р геол.-минерал. наук Пермский национальный исследовательский политехнический университет ▪ Scopus ▪ ResearcherID
2 — ведущий инженер Филиал ООО «ЛУКОЙЛ-Инжиниринг» «ПермНИПИнефть» в г.Перми ▪ Orcid ▪ Elibrary ▪ Scopus

Дата отправки:

2020-06-16

Дата принятия:

2020-11-09

Дата публикации:

2020-12-29

Аннотация

Для решения задач, сопровождающих разработку методов прогнозирования, предложен вероятностный метод анализа данных. На примере карбонатного объекта рассмотрено применение вероятностной методики прогнозирования эффективности технологии пропантного гидравлического разрыва пласта (ГРП). Выполнен прогноз прироста дебита нефти скважин с использованием вероятностного анализа геологических и технологических данных в разные периоды выполнения ГРП. С помощью данного метода размерные показатели были переведены в единое вероятностное пространство, что позволило выполнить сравнение и построить индивидуальные вероятностные модели. Проведена оценка степени влияния каждого показателя на эффективность ГРП. Вероятностный анализ показателей в разные периоды выполнения ГРП позволил выявить универсальные статистически значимые зависимости. Данные зависимости не меняют своих параметров и могут быть использованы для прогнозирования в разные периоды времени. Определены критерии применения технологии ГРП на карбонатном объекте. С использованием индивидуальных вероятностных моделей рассчитаны комплексные показатели, на основе которых построены регрессионные уравнения. С помощью уравнений выполнен прогноз эффективности ГРП на прогнозных выборках скважин. Для каждой из выборок рассчитаны коэффициенты корреляции. Прогнозные результаты хорошо коррелируются с фактическими приростами (значения коэффициентов корреляции r = 0,58-0,67 по экзаменационным выборкам). Вероятностный метод, в отличие от других, обладает простотой и прозрачностью. С его использованием и при тщательном подборе скважин для применения технологии ГРП вероятность получения высокой эффективности значительно возрастает.

Ключевые слова:

гидравлический разрыв пласта геолого-технические мероприятия прирост дебита нефти карбонатный коллектор статистический анализ вероятностный анализ

Галкин В.И., Колтырин А.Н. Исследование вероятностных моделей для прогнозирования эффективности технологии пропантного гидравлического разрыва пласта // Записки Горного института. 2020. Т. 246. С. 650-659. DOI: 10.31897/PMI.2020.6.7

Galkin V.I., Koltyrin A.N. Investigation of probabilistic models for forecasting the efficiency of proppant hydraulic fracturing technology // Journal of Mining Institute. 2020. Vol. 246. p. 650-659. DOI: 10.31897/PMI.2020.6.7

10.31897/PMI.2020.6.7

Введение. Прогнозирование временного ряда является одной из распространенных форм постановки задачи прогнозирования, решение которой играет важнейшую роль в процессах стратегического планирования. Применение каких-либо из существующих в настоящее время математических моделей и методов прогнозирования временных рядов тесно связано со спецификой предметной области. Задача прогнозирования временного ряда решается на основе создания модели прогнозирования, приемлемо описывающей исследуемый процесс.

Рассматриваемый класс временных рядов с регулярными постоянными компонентами используется в предметных областях, в которых существенно влияние различных факторов. Примером такой сферы является нефтяная промышленность, где прибыль компании, страны зависит от уверенности в выполнении планов по добыче нефти. Выполнение планов по добыче нефтизависит от множества факторов: технологических, обусловленных технологией добычи нефти; технических, зависящих от применяемых технических средств для интенсификации добычи нефти и геологических, обусловленных структурой пространства, где располагаются остаточные запасы нефти. Для прогнозирования динамики работы скважины [17, 18, 21] используют совокупность геолого-физических факторов, характеризующих залежь или район скважины.При наличии временных рядов данного класса в разных сферах решение задачи прогнозирования является важной научно-технической задачей.

По состоянию на 01.01.2020г. разработаны и применяются следующие статистические и структурные модели прогнозирования временных рядов: регрессионные модели прогнозирования [6, 9 - 11]; модели, использующие генетические алгоритмы [3]; модель на нейронных сетях [4, 14, 15]; на классификационно-регрессионных деревьях [1]; на марковских процессах [13]; на основе кластеризации [5, 8]; на основе самоорганизующихся карт (карты Кохонена) [2]; на основе нечеткой логики [7], [12]; на байесовских сетях [13].

Все статистические и структурные модели прогнозирования временных рядов имеют свои преимущества и недостатки.

Регрессионные модели и методы. К достоинствам данных моделей относят простоту, гибкость, а также единообразие их анализа. При использовании линейных регрессионных моделей результат прогнозирования может быть получен быстрее, чем при использовании остальных моделей. Кроме того, преимуществом является прозрачность моделирования, т.е. доступность для анализа всех промежуточных вычислений. Основным недостатком нелинейных регрессионных моделей является сложность определения вида функциональной зависимости, а также трудоемкость определения основных параметров модели, участвующих в расчетах.

Нейросетевые модели и методы. Основным достоинством нейросетевых моделей является нелинейность, т.е. способность устанавливать нелинейные зависимости между будущими и фактическими значениями процессов. Другие важные достоинства: адаптивность, масштабируемость и единообразие анализа и проектирования. Недостатки: отсутствие прозрачности моделирования, сложность выбора архитектуры, высокие требования к непротиворечивости обучающей выборки, сложность выбора алгоритма обучения и ресурсоемкость процесса обучения.

Модели на базе классификационно-регрессионных деревьев. Достоинства данного класса моделей: масштабируемость (за счет которой возможна быстрая обработка сверхбольших объемов данных), быстрота и однозначность процесса обучения дерева, а также возможность использования категориальных внешних факторов. Недостатки: неоднозначность алгоритма построения структуры дерева, сложность определения момента прекращения дальнейшего ветвления.

Судить о точности прогнозирования приведенных моделей прогнозирования не представляется возможным. Точность прогнозирования того или иного процесса зависит не только от модели, но и от опыта исследователя, от того, насколько хорошо он разобрался в устройстве той или иной модели прогнозирования, от доступности данных и многих других факторов. Однако можно сгруппировать основные недостатки существующих методов прогнозирования: большое число свободных параметров, требующих идентификации; различные размерности, используемые при прогнозировании показателей; недоступность промежуточных вычислений, выполняющихся в «черном ящике»; сложность оценки индивидуальной степени влияния используемых показателей на выходное значение, т.е.зачастую бывает трудно определить, какие из показателей имеют наибольшее влияние на выходной показатель и ранжировать их.

Задача прогнозирования временных рядов актуальна для многих предметных областей и является важной частью повседневной работы компаний ООО «ЛУКОЙЛ-Пермь». Для решения данных задач предлагается рассмотреть возможности использования вероятностного метода, который достаточно подробно изложен в работах [16, 19, 22, 23]. В данной работе выполнен прогноз прироста дебита нефти $q_{н . п р о г н о з}^{Г Р П}$ с использованием вероятностного метода анализа геологических и технологических данных на примере опыта применения технологии пропантного ГРП на карбонатном объекте В3В4 (верхнекаменноугольные отложения). Геологические и технологические параметры скважин известны на стадии подбора, что позволяет заблаговременно произвести расчеты эффективности технологии и дать рекомендации к ее внедрению.

По состоянию на 01.01.2019 г. на объекте В3В4 выполнено 66 операций пропантного ГРП сосредним начальным приростом дебита нефти 7,1т/сут. Разделим выборку скважин на два класса: класс I с приростом нефти $q_{н . п р о г н о з}^{Г Р П}$ > 7 т/сут – технология является эффективной, класс II с приростом нефти $q_{н . п р о г н о з}^{Г Р П} <$ 7 т/сут – технология малоэффективна. Первоначально для каждого класса по скважинам исследуемых объектов разработки выполнен статистический анализ более 50 показателей. В результате анализа установлены параметры, которые оказывают влияние на эффективность пропантного ГРП. Важность показателей оценивалась путем сравнения средних значений в двух классах по критерию информативности

\begin{matrix} (1) & t_{p} = \frac{❘ X_{1} - X_{2} ❘}{\sqrt{\frac{1}{n_{1}} + \frac{1}{n_{2}} (\frac{(n_{1} - 1) S_{1}^{2} + (n_{2} - 1) S_{2}^{2}}{n_{1} + n_{2} - 2})}}, \end{matrix}

где, $X_{1}$ , $X_{2}$ - средние значение показателей для сквадин классов I и II; S²₁, S²₂ - дисперсии показателей.

Критерий t_p позволил сократить первоначально имеющееся количество показателей до нескольких.

Основные геолого-технологические показатели:

• Геологические параметры: коэффициенты пористости m_пор %; продуктивности К_прод, м³сут МПа; проницаемости ближней зоны пласта К^ПЗП_прон, мкм²; проницаемости удаленной зоны пласта К^УЗП_прон, мкм²; пьезопроводности γ, см²·с; скин-фактор S; значения гамма-каротажа GK, мкр/ч; значения гамма нейронного гамма-каротажа NGK, мкр/ч; скрытая эффективная нефтенасыщенная толщина h_эф, м; глубина залегания пласта относительная H_отн, м; абсолютная H_абс, м.

• Технологические параметры: текущее пластовое давление в скважине P_плМПа; накопленная с начала эксплуатации скважиныдобыча нефти Q_н.н, т; добыча воды Q_в.н, т.

Предлагается выполнить вероятностный анализ данных и построить вероятностные модели по геологическим и технологическим показателям скважин, сформированным в периоды: 2014-2015 (20 скв.); 2014-2016 (29 скв.); 2014-2017 (50 скв.); 2014-2018 гг. (66 скв.).

Первоначально планируется построить вероятностную модель по скважинам 2014-2015гг., т.е. каждый геолого-технологический параметр N, имеющий размерность (МПа, мкм², т и т.д.), перевести в безразмерную величину. Перевод размерных величин в безразмерные позволит сравнивать показатели в едином вероятностном пространстве между собой. По результатам анализа по каждому показателю построим вероятностное уравнение:

\begin{matrix} (2) & P (N) = A + B N, B = t g α \end{matrix}

Вероятностное уравнение позволит определить критерии применения технологии ГРП и ранжировать показатели по степени влияния на фактический прирост дебита нефти $q_{н . ф а к т}^{Г Р П}$ . Будем считать прирост дебита нефти 7т/сут достижимым, если вероятность P(N) ≥ 0,5 д.ед., данная величина будет минимальным критерием применения технологии. Степень влияния $q_{н . ф а к т}^{Г Р П}$ определим как разность максимальной и минимальной величин P(N). После анализа планируется добавить девять скважин 2016 года и выполнить анализ характеристик. С добавлением в выборку новых скважин (2016-2018гг.) вероятностные модели пересчитываются, анализируются изменения коэффициента B, меняются критерии применения технологии.

Рассмотрим методику построения индивидуальных вероятностных моделей на примере текущего пластового давления в скважине $P_{п л}$ . Средние значения показателя для скважин, где технология ГРП эффективна и малоэффективна, отличаются в 1,1 раза. В классе I средняя величина $P_{п л}$ =7,7 МПа, в классе II $P_{п л}$ =6,8 МПа. Далее по данной характеристике исследовались плотности распределений изучаемых двух классов. В первом случае изучаются данные по значениям класса I, $n_{(} 1)$ =38, во втором - данные класса II $n_{(} 2)$ =28.

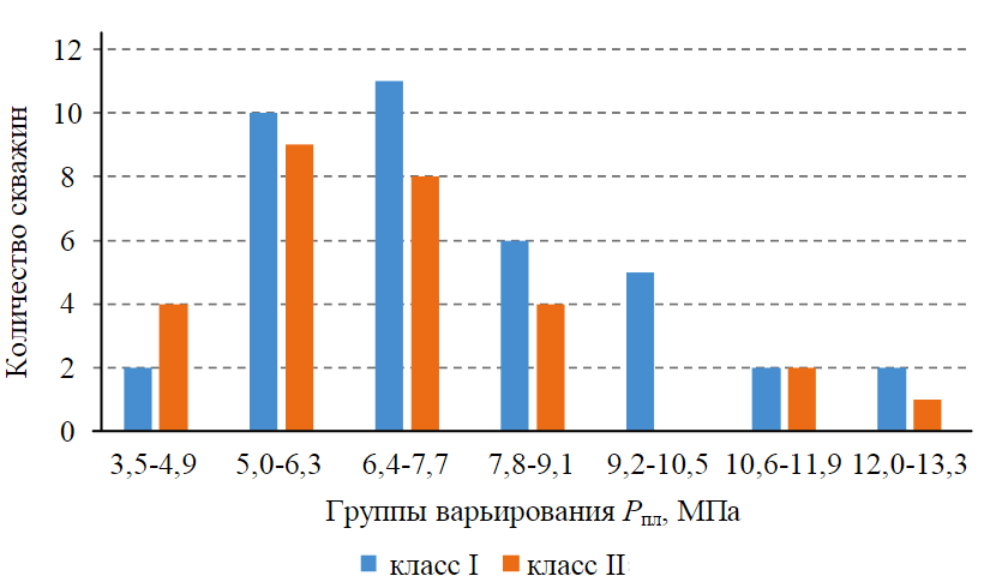
Рис.1. Гистограмма зависимости количества скважин от групп варьирования пластового давления

P_{п л}

Следуя используемой методике,на первом этапе построения вероятностной модели по даннымпоказателя $P_{п л}$ для классов I и II строится гистрограмма. Оптимальные величины интервалов значений показателя $P_{п л}$ вычислляются по формуле Стерджесса:

\begin{matrix} (3) & Δ X = \frac{X_{\max} - X_{\min}}{1 + 3, 23 lgN} = \frac{13, 2 - 3, 5}{1 + 3, 23 \lg 66} = 1, 4. \end{matrix}

Для исследования соотношений доли значений, попавших в различные интервалы варьирования $P_{п л}$ , выполнен интервальный анализ (рис.1).

На следующем шаге вычисляем вероятность принадлежности группы к классу:

\begin{matrix} (4) & P (P_{п л}) = \frac{N_{g}}{N_{k}}, \end{matrix}

где $N_{g}$ - число случаев содержания $P_{п л}$ к группе; $N_{k}$ - объем выборки для классов I и II.

Результаты расчетов представлены в табл.1.

Таблица 1

Распределение значений вероятностей P(P_пл) принадлежности групп к классам

Скважины	Интервалы варьирования пластового давления $P_{п л}$ , $с м^{2}$ /с
Скважины	3,5-4,9	5,0-6,3	6,4-7,7	7,8-9,1	9,2-10,5	10,6-11,9
Класс I при $n_{1}$ =38	0,053	0,263	0,289	0,158	0,132	0,053
Класс II при $n_{2}$ =28	0,143	0,321	0,286	0,143	-	0,071

Далее рассчитаем условную вероятность для каждой группы:

\begin{matrix} (5) & P (P_{п л}) = \frac{\frac{N_{g}}{N_{k = 1}}}{\frac{N_{g}}{N_{k = 1}} + \frac{N_{g}}{N_{k = 2}}} \end{matrix}

В каждом интервале вычисляются вероятности принадлежности к скважинам класса I. После этого интервальные вероятности принадлежности к классу I сопоставляются со средними интервальными значениями показателя P_пл. По величинам P(P_пл) и P_пл высчитывается парный коэффициент корреляции r и строится уравнение регрессии. Последующая корректировка построенных моделей выполняется с условием, что среднее значение вероятностей для скважин,где ГРП эффективно, должно быть больше 0,5, а скважин, где ГРП малоэффективно, меньше 0,5. Вероятностная модель имеет следующий вид:

\begin{matrix} (6) & P (P_{п л}) = 0, 023 - 0, 057 P_{п л} \end{matrix}

В табл.2 представлены модели геолого-технологических параметров по каждой из выборок. Показано, что значения вероятностей по всем показателям изменяются в пределах 0,160-0,840. Это свидетельствует о том, что все показатели с различными размерностями при помощи построенных уравнений регрессии были переведены в единое вероятностное пространство. Выполняемые вычисления для построения индивидуальных вероятностных моделей доступны для специалиста и, в отличие от других методов, не содержат скрытых процессов.

Таблица 2

Вероятностные модели принадлежности к классу I (по выборкам)

Выборка скважин	Вероятностное уравнение	Область применения уравнения		Диапазон изменения вероятности
Геологические параметры
2014-2015	$P (S) = 0, 025 - 0, 126 S$	-6,2	-1,3	0,190	0,810
2014-2016	$P (S) = 0, 189 - 0, 0082 S$	-6,2	-1,3	0,297	0,703
2014-2017	$P (S) = 0, 369 - 0, 038 S$	-6,6	-0,2	0,377	0,623
2014-2018	$P (S) = 0, 444 - 0, 040 S$	-6,6	3,8	0,292	0,708
2014-2015	$P (N G K) = 0, 050 - 0, 120 N G K$	1,2	6,3	0,194	0,806
2014-2016	$P (N G K) = 0, 050 - 0, 120 N G K$	1,2	6,3	0,160	0,840
2014-2017	$P (N G K) = 0, 127 - 0, 101 N G K$	1,1	6,3	0,238	0,782
2014-2018	$P (N G K) = 0, 147 - 0, 095 N G K$	1,1	6,6	0,252	0,748
2014-2015	$P (h_{э ф}) = 0, 866 - 0, 081 h_{э ф}$	3	6	0,378	0,622
2014-2016	$P (h_{э ф}) = 0, 065 - 0, 113 h_{э ф}$	3	7	0,274	0,726
2014-2017	$P (h_{э ф}) = 0, 943 - 0, 093 h_{э ф}$	2,5	7	0,290	0,710
2014-2018	$P (h_{э ф}) = 0, 837 - 0, 071 h_{э ф}$	2,5	7	0,340	0,660
2014-2015	$P (H_{о т н}) = 2, 936 - 0, 002 H_{о т н}$	1036	1252	0,307	0,761
2014-2016	$P (H_{о т н}) = - 0, 726 - 0, 001 H_{о т н}$	1036	1288	0,413	0,690
2014-2017	$P (H_{о т н}) = 0, 238 - 0, 0002 H_{о т н}$	1036	1288	0,446	0,497
2014-2018	$P (H_{о т н}) = - 0, 105 - 0, 0005 H_{о т н}$	1036	1288	0,413	0,539
2014-2015	$P (m) = - 0, 687 - 0, 072 m$	14,3	18,5	0,348	0,652
2014-2016	$P (m) = 0, 184 - 0, 021 m$	11,4	18,5	0,425	0,575
2014-2017	$P (m) = - 0, 636 - 0, 074 m$	11,4	19,1	0,213	0,786
2014-2018	$P (m) = 0, 042 - 0, 029 m$	11,4	19,4	0,377	0,612
2014-2015	$P (γ) = 0, 653 - 0, 0005 γ$	27	617	0,3454	0,640
2014-2016	$P (γ) = 0, 605 - 0, 0003 γ$	17	617	0,421	0,601
2014-2017	$P (γ) = 0, 729 - 0, 0007 γ$	17	617	0,297	0,717
2014-2018	$P (γ) = 0, 479 - 0, 00007 γ$	6	669	0,480	0,526
2014-2015	$P (K_{п р о д}) = 0, 322 - 0, 039 K_{п р о д}$	0,39	8,54	0,338	0,662
2014-2016	$P (K_{п р о д}) = 0, 359 - 0, 032 K_{п р о д}$	0,21	8,54	0,366	0,634
2014-2017	$P (K_{п р о д}) = 0, 444 - 0, 012 K_{п р о д}$	0,21	8,54	0,447	0,553
2014-2018	$P (K_{п р о д}) = 0, 446 - 0, 012 K_{п р о д}$	0,07	8,54	0,447	0,553
2014-2015	$P (H_{а б с}) = - 6, 211 + 0, 007 H_{а б с}$	848	876	0,403	0,622
2014-2016	$P (H_{а б с}) = - 14, 585 + 0, 017 H_{а б с}$	848	876	0,255	0,745
2014-2017	$P (H_{а б с}) = 0, 164 + 0, 0003 H_{а б с}$	844	876	0,418	0,428
2014-2018	$P (H_{а б с}) = 0, 141 + 0, 0003 H_{а б с}$	840	876	0,394	0,404
2014-2015	$P (K_{п р о н}^{П З П}) = 0, 457 + 0, 376 K_{п р о н}^{П З П}$	0,006	0,192	0,4460	0,530
2014-2016	$P (K_{п р о н}^{П З П}) = 0, 367 + 1, 473 K_{п р о н}^{П З П}$	0,002	0,192	0,371	0,649
2014-2017	$P (K_{п р о н}^{П З П}) = 0, 469 + 0, 236 K_{п р о н}^{П З П}$	0,002	0,192	0,470	0,515
2014-2018	$P (K_{п р о н}^{П З П}) = 0, 490 + 0, 036 K_{п р о н}^{П З П}$	0,002	0,206	0,491	0,498
2014-2015	$P (G K) = 0, 524 - 0, 009 G K$	1,4	4	0,488	0,512
2014-2016	$P (G K) = 0, 402 - 0, 036 G K$	1,4	4	0,453	0,547
2014-2017	$P (G K) = 0, 392 + 0, 041 G K$	1,2	4	0,442	0,558
2014-2018	$P (G K) = 0, 368 + 0, 050 G K$	1,2	4	0,429	0,571
2014-2015	$P (K_{п р о н}^{У З П}) = 0, 554 + 1, 515 K_{п р о н}^{У З П}$	0,003	0,069	0,449	0,550
2014-2016	$P (K_{п р о н}^{У З П}) = 0, 479 + 0, 588 K_{п р о н}^{У З П}$	0,001	0,069	0,479	0,520
2014-2017	$P (K_{п р о н}^{У З П}) = 0, 540 + 0, 882 K_{п р о н}^{У З П}$	0,001	0,069	0,480	0,540
2014-2018	$P (K_{п р о н}^{У З П}) = 0, 622 - 1, 211 K_{п р о н}^{У З П}$	0,001	0,19	0,392	0,621
Технологические параметры
2014-2015	$P (Q_{В . Н .}) = 0, 378 + 0, 00004 Q_{В . Н .}$	91	6747	0,382	0,648
2014-2016	$P (Q_{В . Н .}) = 0, 425 + 0, 00001 Q_{В . Н .}$	91	16513	0,426	0,591
2014-2017	$P (Q_{В . Н .}) = 0, 425 + 0, 000006 Q_{В . Н .}$	91	16513	0,452	0,551
2014-2018	$P (Q_{В . Н .}) = 0, 399 + 0, 000009 Q_{В . Н .}$	91	16513	0,399	0,548
2014-2015	$P (Q_{Н . Н .}) = 0, 218 + 0, 00001 Q_{Н . Н .}$	939	49280	0,228	0,711
2014-2016	$P (Q_{Н . Н .}) = 0, 392 + 0, 000004 Q_{Н . Н .}$	939	49280	0,396	0,589
2014-2017	$P (Q_{Н . Н .}) = 0, 459 + 0, 000001 Q_{Н . Н .}$	939	59862	0,461	0,520
2014-2018	$P (Q_{Н . Н .}) = 0, 454 + 0, 000002 Q_{Н . Н .}$	841	59862	0,455	0,574
2014-2015	$P (P_{П Л}) = 0, 279 + 0, 037 P_{П Л}$	3,5	8,4	0,408	0,592
2014-2016	$P (P_{П Л}) = 0, 054 + 0, 063 P_{П Л}$	3,5	10,6	0,274	0,726
2014-2017	$P (P_{П Л}) = 0, 038 + 0, 055 P_{П Л}$	3,5	13,2	0,231	0,770
2014-2018	$P (P_{П Л}) = 0, 023 + 0, 057 P_{П Л}$	3,5	13,2	0,222	0,778

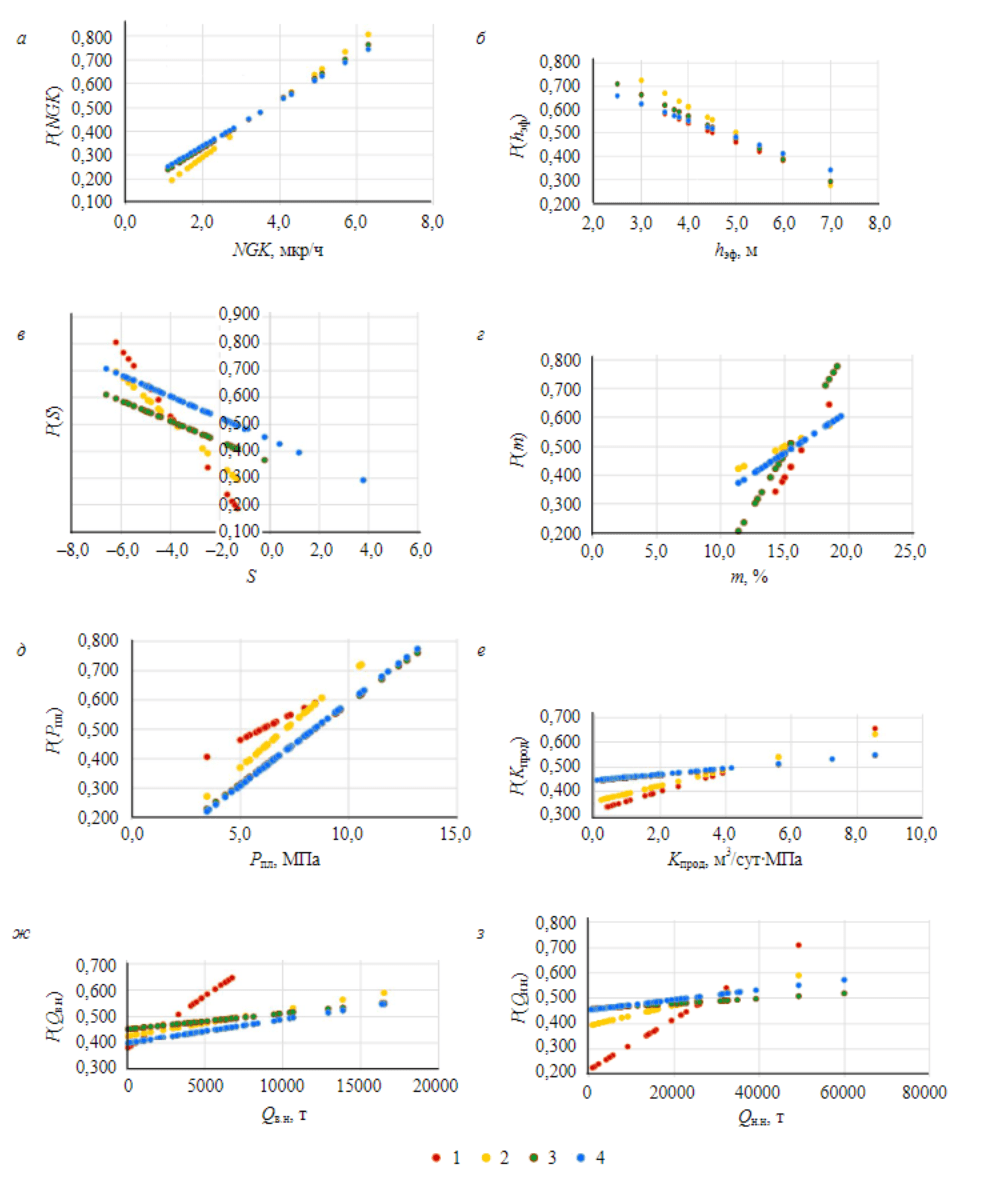
На рис.2 представлены универсальные зависимости, обладающие одинаковыми свойствами во всех выборках. Цветами выделены универсальные зависимости по выборкам скважин периодов: 2014-2015 (красный), 2014-2016 (желтый), 2014-2017 (зеленый), 2014-2018 гг. (синий). Универсальные зависимости будут обладать данными свойствами при увеличении количества скважин в выборке (2019, 2020, 2021, ...). Например, при вероятностном анализе выборки скважин 2014-2015гг. наблюдалось, что с увеличением значений NGK отмечалось увеличение эффективности ГРП P(NGK)→ 1. Добавление новых данных по скважинам из выборок 2016, 2017, 2018гг. не приводит к изменению зависимости. В табл.2 показано, что $t g α$ (2) в четырех случаях изменяется в диапазоне от +0,095 до +0,120. Угол наклона $t g α$ для показателей $h_{э ф}$ , NGK наибольший в сравнении с другими показателями. По геолого-технологическим показателям: S, m, $P_{п л}$ , $Q_{н . н .}$ , $Q_{в . н .}$ , $K_{п р о д}$ $t g α$ → 0. Значение $t g α$ геологического параметра $K_{п р о д}$ изменяются в узком диапазоне от 0,012 до 0,039. Угол наклона $K_{п р о д}$ меньше, чем NGK, что свидетельствует о слабом влиянии на выходной показатель. По скважинам из выборки 2014-2015 гг. по параметру $K_{п р о д}$ отмечается наибольшее значение $t g α$ , с каждым добавлением новых скважин в выборку $t g α$ → 0. Вероятно, при увеличении количества скважин в выборке (2019, 2020, ...) на одном из этапов $t g α$ → 0, т.е. данный параметр не будет оказывать влияния на эффективность ГРП. Параметры $Q_{н . н}$ , $Q_{в . н}$ в выборке 2014-2015гг. обладают наибольшим $t g α$ = 45 град, с добавлением в выборку скважин из 2016, 2017, 2018 гг. $t g α$ → 0, что свидетельствует о слабом влиянии на выходной показатель.

Рис.2. Универсальные зависимости геолого-технологических параметров: a – P(NGK); б – P(

h_{э ф}

) от

h_{э ф}

; в – P(S) от S; г – P(m) от m; д – P(

P_{п л}

) от

P_{п л}

; е – P(

K_{п р о д}

) от

K_{п р о д}

; ж – P(

Q_{в . н}

) от

Q_{в . н}

; з – P(

Q_{н . н}

) от

Q_{н . н}

; 1 – ГРП 2014-2015; 2 – ГРП 2014-2016; 3 – ГРП 2014-2017; 4 – ГРП 2014-2018 гг.

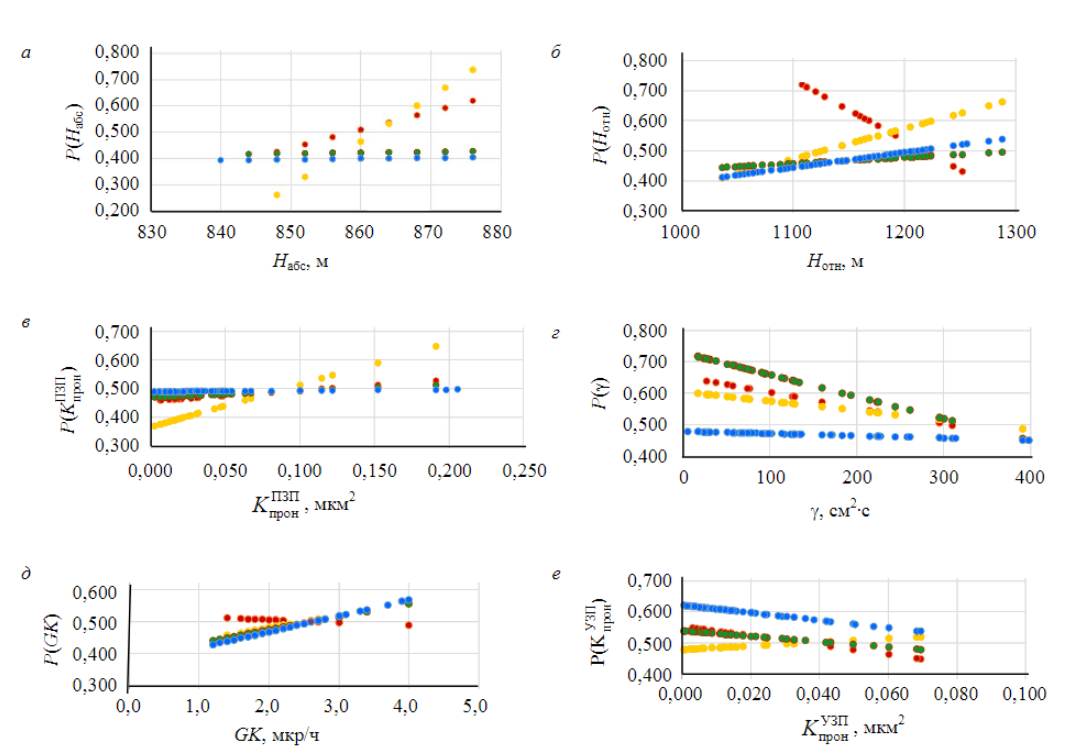
На рис.3 цветными точкамиобозначены нечеткие зависимости по выборкам скважин периодов: 2014-2015, 2014-2016, 2014-2017, 2014-2018гг. Глубина залегания пласта значительно влияет на эффективность ГРП в период 2014-2015гг., при увеличении значений tg $α$ → 0, что показывает отсутствие влияния параметра. Отсутствие влияния параметра сигнализирует о том, что вклассах I и II большинство скважин располагается на одинаковых абсолютных и относительных глубинах. Изменение направления зависимости относительной глубины залегания пласта $H_{о т н}$ сплюса на минус в табл.2 сигнализирует об изменении соотношения количества скважин, принадлежащих классам I и II. Зависимости, построенные по выборке скважин 2014-2018гг., обладают слабым влиянием на выходной показатель tg $α$ → 0 (P(N) → 0,5).

Рис.3. Зависимости геолого-технологических параметров: a – P(

H_{а б с})

от \(H_{абс})\; б – P(

H_{о т н})

от

H_{о т н}

; в – P(

K_{п р о н}^{П З П})

от

K_{п р о н}^{П З П}

; г – P(

γ

) от

γ

; д – P(GK) от GK; e – P(

K_{п р о н}^{У З П}

) от

K_{п р о н}^{У З П}

1 – ГРП 2014-2015; 2 – ГРП 2014-2016; 3 – ГРП 2014-2017; 4 – ГРП 2014-2018 гг.

Рис.4. Корреляционные поля по обучающим выборкам скважин: a – 2014-2015 гг. (2016-2018 гг. прогнозная выборка, максимальное отклонение 2,9 т/сут); б – 2014-2016 гг. (2017-2018 гг. прогнозная выборка, максимальное отклонение 2,4 т/сут); в – 2014-2017 гг. (2018 г. прогнозная выборка, максимальное отклонение 2 т/сут); г – 2014-2018 гг. (максимальное отклонение 1,4 т/сут) 1 – обучение; 2 – прогноз

Вероятностный метод анализа данных обладает «прозрачностью», так как на практике получилось построить вероятностные модели и оценить степень влияния показателей на выходной показатель $q_{н . ф а к т}^{Г Р П}$ . Сопоставленывходные параметрыс различной размерностью вследствиеприведения их в единое пространство размерности.

Определены наиболее информативные параметры, влияющие на выходной параметр. Выявлены универсальные зависимости, ранжированы по углу наклона tg $α$ , т.е.определены параметры показателей, имеющие наибольшее влияние на выходной показатель, и в зависимости от этого распределены. В случае tg $α \sim$ 0 геолого-технологические параметры не оказывают влияния, и ими можно пренебречь. Таким образом можно определить только необходимые параметры, что позволяет в дальнейшем проводить анализ универсальных моделей.

Для достижения прироста дебита нефти 7 т/сут необходимо, чтобы вероятность была более 50%. Следовательно, значения критериев применения технологии ГРП располагается в пределах 0,5-1д.ед. (P(N) ≥ 0,5). Таким образом (P(N) = 0,5 соответствует минимальному значению параметра, (P(N) → 1 соответствует максимальному. Универсальные показатели должны соответствовать критериям применения технологии ГРП на карбонатном объекте В3В4:значения гамма-каротажа NGK = 4,1-6,3 мкр/ч; вскрытая эффективная нефтенасыщенная толщина $h_{э ф}$ = 4,5-2,5 м; скин-фактор S = (–1,4-–6,6); коэффициент пористости m = 16,1-19,4%; текущее пластовое давление в скважине $P_{п л}$ = 8,2-13,2 МПа; коэффициент продуктивности $K_{п р о д}$ = 4,2-8,5 м³/сут∙МПа; накопленная добыча нефти с начала эксплуатации скважины $Q_{н . н}$ = 10682-16523т; накопленная добыча воды с начала эксплуатации скважины $Q_{в . н .}$ = 22810-59802 т.

Прогнозирование прироста дебита нефти. С целью совместного использования индивидуальных вероятностей по геолого-технологическим показателям вычисляется обобщенная (комплексная) вероятность $P_{к о м п}$ [16, 20]. Сначала комплексная вероятность рассчитывается для двух показателей $P_{к о м п_{m}^{2}}$ , на последнем шаге – для восьми показателей $P_{к о м п_{m}^{8}}$ .

Прогнозный прирост дебита нефти $q_{н . п р о г н о з}^{Г Р П}$ для каждой из выборок рассчитывается с помощью пошагового регрессионного анализа с использованием значений $P_{к о м п}$ при m от 2 до 8 для геолого-технологических параметров. Уравнение регрессии для выборки скважин 2014-2015гг.имеет следующий вид:

q_{н . п р о г н о з}^{Г Р П (2014 - 2015)} = 4, 12 + 19, 1 P_{к о м п_{m}^{3}} + 27, 7 P_{к о м п_{m}^{4}} + 15, 8 P_{к о м п_{m}^{5}} .

Данная регрессионная модель учитывает значения $P_{к о м п}$ при сочетании m = 3, что позволяет прогнозировать прирост дебита нефти (по скважинам 2016-2018 гг.) с максимальным отклонением от фактических значений 2,9т/сут.Аналогично строится уравнение регрессии и проводится прогноз для скважин выборок 2014-2016, 2014-2017, 2014-2018 гг.

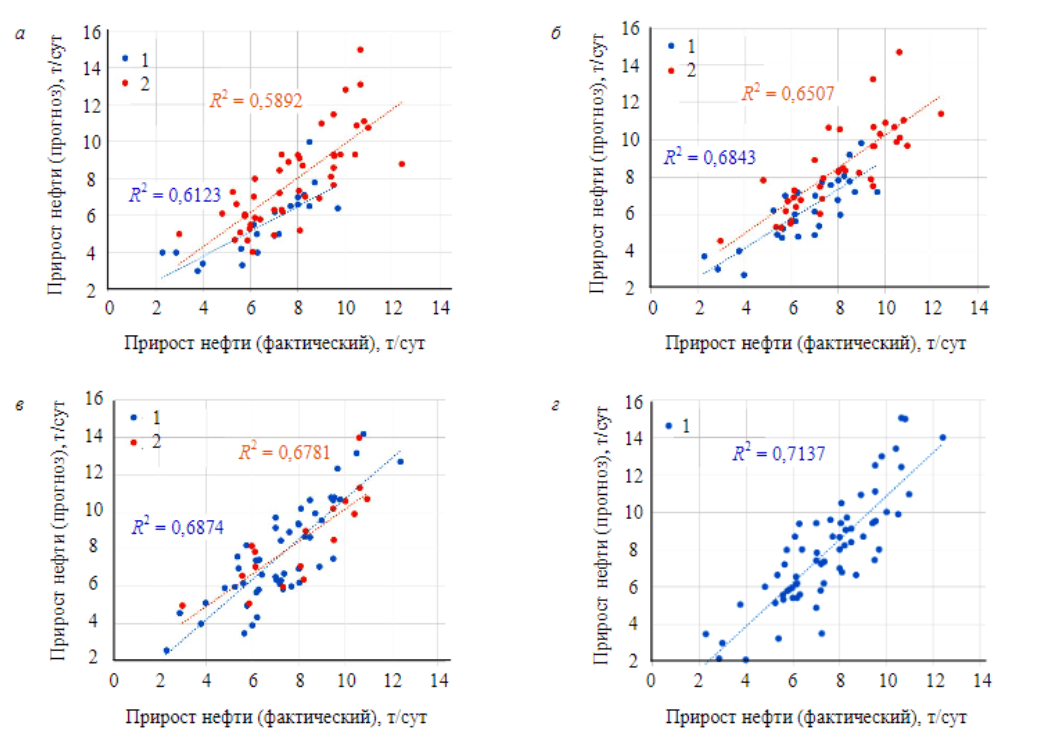
На рис.4 показано, что рассчитанные значения прироста дебита нефти достаточно хорошокоррелируется с фактическими приростами дебитов, значения коэффициентов корреляции r = 0,58-0,67 по экзаменационным выборкам скважин. Наибольшее расхождение прогнозных данных с фактическими наблюдается при прогнозировании приростов в период 2016-2018гг., максимальное отклонение 2,9т/сут, в других выборках отмечается наименьшее отклонение. Наименьшее расхождение при прогнозировании приростов дебитов нефти в обучающей выборке скважин 2014-2018 гг.

Заключение. Главными достоинствами вероятностного метода анализа являются простота и прозрачность. Данный метод позволил значительно сократить число свободных переменных,перевести размерные показатели в единое вероятностное пространство.

Описание построения индивидуальных вероятностных моделей позволило показать прозрачность данного метода и отсутствие скрытых процессов. С помощью tg $α$ определено, какие из показателей имеют наибольшее влияние на выходной показатель. Благодаря вероятностному представлению данных по каждому параметру определены критерии применения технологии ГРП на объекте В3В4, выявлены допустимые вероятностные пределы применения технологии. Анализ выполненных прогнозов позволил определить достоверность построенныхрегрессионных моделей.

Метод рекомендуется использовать для прогнозирования эффективности применения других технологий: перфорационных методов, радиального бурения, кислотных обработок и др.

Литература

Галкин В.И. Вероятностно-статистическая оценка использования различных показателей для определения эффективности применения пропантного ГРП (на примере терригенного объекта Тл-Бб и карбонатного объекта $В_{3}$ $В_{4}$ / В.И.Галкин, А.С.Казанцев, А.Н.Колтырин // Нефтепромысловое дело. 2018. No 2. С. 26-32. DOI: 10.30713/0207-2351-2018-2-26-33
Галкин В.И. Разработка вероятностно-статистических моделей для оценки эффективности применения пропантного гидравлического разрыва пласта (на примере объекта Тл-Бб Батырбайского месторождения) / В.И.Галкин, И.Н.Пономарева, А.Н.Колтырин // Вестник Пермского национального исследовательского политехнического университета. Геология. Нефтегазовое и горное дело. 2018. T. 18. No 1. С. 37-49. DOI: 10.15593/2224-9923/2018.1.4
Галкин В.И. Разработка геолого-математических моделей для прогноза нефтегазоносности сложнопостроенных структур в девонских терригенных отложениях / В.И.Галкин, Н.Е.Соснин // Нефтяное хозяйство. 2013. No 4. С. 28-31.
Методика выбора скважин-кандидатов для проведения повторного гидроразрыва пласта на основе эффекта переориентации трещины / П.Д.Савченко, А.И.Федоров, А.В.Колонских, Р.Ф.Уразбахтин, А.Р.Давлетова // Нефтяное хозяйство. 2017. No 11. С. 114-117. DOI: 10.24887/0028-2448-2017-11-114-117
Соснин Н.Е. Разработка статистических моделей для прогноза нефтегазоносности (на примере терригенных девонских отложений Северо-Татарского свода) // Вестник Пермского национального исследовательского политехнического университета. Геология. Нефтегазовоедело. 2012. T. 11. No 5. С. 16-25.
Alimkhanov R. Application of Data Mining Tools for Analysis and Prediction of Hydraulic Fracturing Efficiency for the BV8 Reservoirof the Povkh Oil Field (Russian) / R.Alimkhanov, I.Samoylova // SPE Russian Oil and Gas Exploration & Production Technical Conference and Exhibition, 14-16 October 2014. Moscow, Russia, 2014. SPE-171332-RU. DOI: 10.2118/171332-RU
Anifowose F. Fuzzy logic-driven and SVM-driven hybrid computational intelligence models applied to oil and gas reservoir characterization / F.Anifowose, A.Abdulraheem // Journal of Natural Gas Science and Engineering. 2011. Vol. 3. No 3. P.505-517. DOI: 10.1016/j.jngse.2011.05.002
Aryanto А. Hydraulic fracturing candidate-well selection using artificial intelligence approach / А.Aryanto, S.Kasmungin, F.Fathaddin // Journal of Natural Gas Science and Engineering. 2018. Vol. 2. No 2. P.53-59. DOI: 10.33021/jmem.v2i02.322
Ashena R. Bottom hole pressure estimation using evolved neural networks by real coded ant colony optimization and genetic algorithm / R.Ashena, J.Moghadasi // Journal of Petroleum Science and Engineering. 2011. Vol. 77. No 3-4. P. 375-385. DOI:10.1016/j.petrol.2011.04.015
Bayesian Probabilistic Decline Curve Analysis Quantifies Shale Gas Reserves Uncertainty / X.Gong, R.Gonzalez, D.McVay, J.D.Hart // Canadian Unconventional Resources Conference, 15-17 November 2011, Calgary, Alberta, Canada, 2011. SPE147588. DOI: 10.2118/147588-MS
Clark A.J. Production Forecasting with Logistic Growth Models / A.J.Clark, L.W.Lake, T.W.Patzek // SPE Annual Technical Conference and Exhibition, 30 October – 2 November 2011, Denver, Colorado, USA, 2011. SPE 144790-MS. DOI:10.2118/144790-MS
Comparison of Candidate-Well Selection Mathematical Models for Hydraulic Fracturing / T.Yu, X.Xie, L.Li, W.Wu // FuzzySystems & Operations Research and Management. Springer, Cham, 2015. Vol. 367. P. 289-299. DOI: 10.1007/978-3-319-19105-8_27
Ma X. Predicting the oil field production using the novel discrete GM (1, N) model / X.Ma, Z.Liu // The Journal of Grey System. 2015. Vol. 27. Iss. 4. P. 63-73.
Mattar L. Production Analysis and Forecasting of Shale Gas Reservoirs: Case History-Based Approach // SPE Shale Gas Production Conference, 16-18 November 2008. Fort Worth, Texas, USA, 2008. SPE 119897-MS. DOI: 10.2118/119897-MS
McVay D.A. The Value of Assessing Uncertainty / D.A.McVay, M.N.Dossary // SPE Journal. 2014. Vol. 6. Iss. 2. P. 100-110. DOI: 10.2118/160189-PA
Mohaghegh S. Development of an intelligent systems approach for restimulation candidate selection / S.Mohaghegh, S.Reeves, D.Hill // SPE/CERI Gas Technology Symposium, 3-5 April 2000, Calgary, Alberta, Canada, 2000. SPE-59767-MS. DOI:10.2118/59767-MS
Petrakov D.G. The effect of fluid saturation on the elastic-plastic properties of oil reservoir rocks / D.G.Petrakov, K.S.Kupavykh, A.S.Kupavykh // Curved and Layered Structures. 2020. Vol. 7. No 1. P. 29-34. DOI: 10.1515/cls-2020-0003
Podoprigora D.G. Development of acid composition for bottom-hole formation zone treatment at high reservoir temperatures / D.G.Podoprigora, L.A.Saychenko // Espacios. 2017. Vol. 48. No 38. P. 32.
Practical Application of a Probabilistic Approach to Estimate Reserves Using Production Decline Data / Y.Cheng, Y.Wang, D.McVay, W.J.Lee // SPE Economics and Management. 2010. Vol.2. Iss. 1. P. 19-31. DOI: 10.2118/95974-PA
Rahmanifard H. Application of artifcial intelligence techniques in the petroleum industry: a review / H.Rahmanifard, T.Plaksina // Artifcial Intelligence Review. 2019. Vol. 52. P. 2295-2318. DOI: 10.1007/s10462-018-9612-8
Sandyga M.S. Formation damage induced by wax deposition: laboratory investigations and modeling / M.S.Sandyga, I.A.Struchkov, M.K.Rogachev // Journal of Petroleum Exploration and Production Technology. 2020. Vol. 10. No 6. P.2541-2558. DOI: 10.1007/s13202-020-00924-2
Schapire R.E. Boosting. Foundations and algorithms / R.E.Schapire, Y.Freund. Cambridge: The MIT Press, 2012. 544 p.
Yanfang W. Refracture candidate selection using hybrid simulation with neural network and data analysis techniques / W.Yanfang, S.Salehi // Journal of Petroleum Science and Engineering. 2014. Vol. 123. P. 138-146. DOI: 10.1016/j.petrol.2014.07.036

Исследование вероятностных моделей для прогнозирования эффективности технологии пропантного гидравлического разрыва пласта

Аннотация

Похожие статьи