Сравнительный анализ фракционирования изотопов азота и углерода при образовании алмаза на основе определения β-факторов
- д-р геол.-минерал. наук ведущий научный сотрудник Институт геологии и геохронологии докембрия РАН ▪ Orcid
Аннотация
Приведены первые количественные оценки изотопного фракционирования азота при кристаллизации алмаза относительно азотсодержащих соединений флюида с использованием квантово-механических (DFT) расчетов по дефектной (с азотом замещения) решетке алмаза. При равновесном фракционировании изотопов 15N/14N уменьшается в ряду соединений NH4+ > N2 > (алмаз, NH3) > CH3N > CN− > NH2. При температуре 1100-1200 °C фракционирование между алмазом и азотсодержащими компонентами флюида оценивается как –2,23, –0,77, 0,01, 0,44, 1,31 и 2,85 ‰ и существенно (более чем на 1 ‰) выше имеющихся оценок, ранее полученных на основе моделирования связи C-N в алмазе по аналогии с молекулами HCN или CN–. В зависимости от преобладающих субстанций азота и углерода в минералообразующем флюиде образование алмаза может сопровождаться различными трендами изменения изотопного состава, что выражается как зональностью отдельных зерен алмаза, так и ковариациями изотопного состава δ15N vs δ13C при последовательной кристаллизации. В условиях доминирования NH3 изотопное фракционирование азота между алмазом и флюидом не превышает 0,1-0,2 ‰ и изотопные сдвиги при температуре ≈1100 °C Δ15N << Δ13C. В бедных азотом восстановленных мантийных флюидах возможное присутствие компонентов с низким сродством к тяжелому изотопу при температуре образования алмаза (особенно NH2) обуславливает высокое изотопное фракционирование алмаз-флюид и повышенные отношения Δ15N/Δ13C. Окисленные флюиды с преобладанием CO2 или CO3 в сочетании с компонентом N2 характеризуются близкими к нулю отношениями Δ15N/Δ13C между алмазом и флюидом за счет преобладания фракционирования изотопов углерода по сравнению с изотопами азота, которые существенно меняются в зависимости от коэффициента распределения азота между алмазом и средой роста.
Финансирование
Работа выполнена в рамках темы НИР FMVW-2021-0003.
Введение
Условия роста и преобразования алмаза отображаются в его морфологических свойствах, спектроскопических особенностях, составе примесей [1-3] и включений [4, 5]. Один из важнейших индикаторов условий образования – изотопный состав углерода алмаза – характеризует как исходный субстрат (эклогиты, перидотиты, вебстериты с разной долей осадочной и мантийной компонент), так и минералообразующий флюид (окисленный, восстановленный, мантийный, поверхностный) [6]. Алмаз может представлять наиболее древние изолированные части мантии [7] и таким образом сохранять изотопные метки углерода начиная с ранних стадий формирования Земли. Помимо углерода для алмаза характерны значительные количества азота (до тысяч и даже десятков тысяч ppm в субдукционных микроалмазах), вхождение которого обусловлено минералообразующими флюидами [8]. Сочетание изотопных систем 12C-13C, 14N-15N широко применяется не только для оценки условий формирования, но и характеристики циклов углерода и азота в глубинных условиях. Очень высокая устойчивость углерода и азота в алмазе [9] способствует сохранности изотопных систем как в условиях формирования на больших (>110 км) глубинах, так и при подъеме к поверхности. Сочетание двух элементов в алмазе представляет уникальную возможность изучения мантии Земли до глубины около 800 км и возраста до 3,5 млрд лет [10]. Учитывая низкое в целом содержание азота в верхней мантии, изотопное отношение 15N/14N алмаза могло бы являться чувствительным показателем смешения мантийного и осадочного резервуаров [11].
Наблюдаемые в алмазе значительные вариации изотопного состава можно объяснять как изотопной неоднородностью, в том числе смешением, исходного субстрата, так и фракционированием изотопов при кристаллизации. Для количественной характеристики процессов, относящихся к образованию алмаза, первостепенное значение имеет определение величины изотопного фракционирования между алмазом и средой, из которой он кристаллизуется. Факторы изотопного фракционирования углерода в зависимости от температуры определены для многих систем, относящихся к образованию алмаза, включая алмаз-CO2, алмаз-CaCO3, алмаз-CH4 и ряд других [12-14]. В отличие от изотопов углерода, фракционирование изотопов азота для алмаза практически не изучено. Экспериментальных данных по распределению изотопов азота между алмазом и потенциальными азотсодержащими веществами в средах роста алмаза до сих пор нет. Известные вычисленные (теоретические) факторы фракционирования изотопов азота ограничиваются отдельными молекулами (NH4+, NH3, N2) в равновесии с произвольными молекулярными аналогами связи C-N алмаза, как HCN или CN– [9]. В отсутствие более или менее надежных определений факторов фракционирования азота между алмазом и мантийным флюидом невозможно, например, разделить процессы смешения азота флюида разных источников, оценить эволюцию изотопного состава при различных механизмах взаимодействия флюида с образующимся алмазом и т.д.
Цель настоящей работы – дать первые количественные оценки равновесного изотопного фракционирования азота при кристаллизации алмаза относительно азотсодержащих соединений флюида с использованием квантово-механических (в рамках теории функционала плотности DFT) расчетов для дефектной (N-содержащей) решетки алмаза и N-содержащих молекул минералообразующего флюида. С целью сравнения расчеты проведены также для алмаза без азота (фракционирование изотопов углерода) и углеродсодержащих молекул флюида.
Методика расчетов
Фактор изотопного фракционирования между фазами A и B, αAB (RA/RB, R – отношение атомных концентраций более тяжелого и легкого изотопов в данном соединении) при изотопном равновесии определяется выражением
где величины β – приведенные отношения статистических сумм рассматриваемых изотопологов, или так называемые β-факторы – без учета ангармоничности рассчитываются из частот колебаний (фононных спектров) изотопологов в зависимости от температуры [15],
или в логарифмической форме
u – безразмерная частота,u = hν/kT; ν – частота колебаний гармонического осциллятора; T – температура, K; h и k – постоянные Планка и Больцмана; верхний индекс * относится к более тяжелому изотопу; нижним индексом i пронумерованы независимые гармонические частоты колебаний соединения. Суммирование производится по всем колебательным состояниям (3N-6 нелинейной молекулы, 3N-5 линейной молекулы, 3N-3 кристалла); N – число атомов соединения. Синус гиперболический sinh(x) ≡ (exp(x) – exp(–x))/2.
Экспериментальные частоты колебаний известны в большинстве случаев только для наиболее распространенных изотопологов (или для их природных смесей) отдельных веществ. Поэтому для определения значений ν приведенного выше соотношения используются методы вычислений «из первых принципов» (abinitio) на основе положения ядер и электронных свойств элементов. В настоящей работе для определения частот колебаний изотопологов применен метод «замороженных фононов» теории функционала плотности, реализованный в программе CRYSTAL (актуальная версия CRYSTAL23 [16]) с использованием набора гауссовых полноэлектронных базисов 6-311G(d). Совокупности базисных функций углерода и азота приведены на сайте программы (https://www.crystal.unito.it/Basis_Sets/). Перед проведением расчетов фононных спектров, выполнена оптимизация параметров внешних орбиталей базисных функций и сравнение значений частот колебаний для кристаллической решетки чистого алмаза и алмаза с разным содержанием примесей азота, а также структурная оптимизация. Среди опробованных функционалов взаимодействия между атомами (в том числе, LDA, GGA, гибридных) минимальное расхождение с экспериментальными значениями вычисленных частот колебаний чистого алмаза получено для функционала WC1LYP. Порог сходимости по энергии для вычислений методом самосогласованного поля (SCF) выбран на уровне 10–11 а.е.м. (Хартри) как при оптимизации структуры, так и при вычислении частот колебаний, а усечение рядов суммирования контролировалось параметрами программы CRYSTAL (TOLINTEG) со значениями (9; 9; 9; 9; 25).
Азот в алмазе находится в различных состояниях, в том числе на месте углерода (азот замещения), и присутствует в разных формах агрегации [17]. Агрегированные формы азота (A- и B-центры) обычно не связываются с исходным образованием дефектов, а считаются вторичными продуктами при долговременном, порядка миллиардов лет, нахождении (естественном отжиге) в условиях высоких температур. При этом агрегация ограничивается перемещением атомов в пределах отдельных зерен и не приводит к изменению общего изотопного баланса кристалла алмаза. В настоящей статье рассмотрены изотопные эффекты, связанные с первичным (при образовании алмаза) вхождением азота на место углерода с возникновением азота замещения (C-центры). Возможность нахождения атомов азота вне C-центра (дислокациях между узлами решетки и т.п.) не рассмотрена, как и вхождение азота в виде A-центра при кристаллизации [18]. Таким образом, атомы углерода при вычислениях замещались атомами азота и определялись энергетически наиболее выгодные конфигурации атомов в структуре алмаза с C-центрами, а затем фононные спектры изотопологов азота с последующим расчетом β-факторов азота замещения. Для адекватного отображения реальных концентраций азота использовался метод расширенных ячеек (суперъячеек) с количеством атомов углерода n = 16; 32; 54; 128 (при замене одного атома углерода на атом азота в кубической решетке). Сходимость результатов достигается при n = 32-54 (что соответствует 20000-30000 ppm и больше, чем максимальная концентрация азота в природных алмазах). Дальнейшее увеличение объема расширенных ячеек вызывает существенные затраты вычислительных ресурсов без какого-либо значимого изменения результатов, в том числе величин β-факторов.
Расчеты β-факторов для молекул, представляющих возможные компоненты флюида при образовании алмаза (к совокупности соединений NH3, NH4+, N2 в работе добавлены NH2, CH3N, C2H6), включали последовательность оптимизации координат ядер с дальнейшим определением колебательных уровней и вычислением величин β. При вычислениях частот колебаний молекулярных соединений использован гибридный функционал B3LYP, наборы базисных векторов качества TVZP в совокупности с дисперсионной поправкой D3 [19], что позволило минимизировать расхождение вычисленных и экспериментально определенных частот. Для еще более точного отображения экспериментальных спектров применен фактор шкалирования SF [20] с приведением рассчитанных частот основного изотополога к экспериментальным и соответствующим изменением частот более тяжелого изотопа.
Значения β-факторов оценивались по соотношению (2) для температур от 0 до 2500 °С с шагом 10 °С. Соответствующие зависимости аппроксимированы полиномами x = 106/T2 (K–2): Результаты для алмаза и молекул приведены в виде полиномов 5-й степени (CO2 и NH2, i = 6) (табл.1). Ошибка аппроксимации во всех случаях не превышает 0,02 ‰ при температурах выше 100 °C и 0,04 ‰ при температурах выше 0 °C (коэффициент детерминации r2 > 0,999).
Результаты
В табл.1 приведены полученные температурные зависимости для расчета β-факторов 15N/14N алмаза. Оценки основаны на вычислениях по расширенной ячейке из 54 атомов. Дальнейшее увеличение объема ячейки (с соответствующим понижением концентрации азота в алмазе) и замещением одного атома C => N не приводит к заметному изменению факторов изотопного фракционирования. Кроме того, в табл.1 представлены как вновь рассчитанные (NH2, CH3N), так и ранее известные
(N2, NH3, NH4+) результаты для вероятных азотсодержащих компонентов мантийных флюидов, а также результаты определения углеродных β-факторов алмаза без примеси азота и β-факторов соединений флюида с углеродом. По представленным данным можно определить (см. соотношение (1) факторы изотопного фракционирования азота (α15/14) и углерода (α13/12) между алмазом и возможными при кристаллизации компонентами флюидов. Далее факторы изотопного фракционирования представляются в виде общепринятых величин Δ = 1000 ln(α).
Таблица 1
Температурные зависимости 1000 lnβ для расчета фракционирования изотопов азота и углерода между алмазом и флюидом
|
Вещество |
a1 |
a2 |
a3 |
a4 |
a5 |
a6 |
Источник |
|
15N/14N |
|||||||
|
Алмаз |
13,13525 +0,05589P |
–0,454961 –0,00471P |
0,023558 +0,00038P |
–0,000965 –1,9619E–5P |
1,92024E–5 +4,3816E–7P |
– |
Данные автора |
|
N2 |
15,27791 |
–2,088265 |
0,248047 |
–0,015932 |
0,0004036 |
– |
[21] |
|
NH3 |
13,91689 |
–2,437494 |
0,339134 |
–0,023827 |
0,0006369 |
– |
[21] |
|
NH4+ |
18,40726 |
–3,003117 |
0,397865 |
–0,027115 |
0,0007104 |
– |
[21] |
|
Алмаз (CN–) |
10,97264 |
–1,275805 |
0,138451 |
–0,008467 |
0,0002086 |
– |
[21] |
|
NH2 |
8,293659 |
–1,827601 |
0,351646 |
–0,038804 |
0,0021684 |
–4,751E–5 |
Данные автора |
|
CH3N |
12,69071 |
–1,384621 |
0,155546 |
–0,009723 |
0,0002388 |
– |
Данные автора |
|
13C/12C |
|||||||
|
Алмаз |
20,931829 +0,10803P |
–0,859144 –0,010389P |
0,048253 +9,129E–4P |
–0,0020401 –4,8886E–5P |
4,09635E–5 +1,115E–6P |
– |
Данные автора |
|
Алмаз |
21,649 0,10768P |
–0,9790 –0,0097P |
0,052834 0,00079P |
–0,001879 –3,7385E–5P |
0,30747E–4 7,6468E–7P |
– |
[22] |
|
Алмаз |
19,856 |
–0,4086 |
– |
– |
– |
– |
[23] |
|
Алмаз |
20,398968 |
–0,858690 |
0,050281 |
–0,002209 |
4,56732E–5 |
|
[24] |
|
Алмаз |
19,949068 +0,08177P |
–0,622300 –0,00609P |
0,014645 +0,00024P |
– |
– |
– |
[6] |
|
CO32– |
24,74146 |
–1,08996 |
0,03178 |
– |
– |
– |
Данные автора |
|
CO2 |
31,32194 |
–3,969173 |
0,485570 |
–0,032037 |
0,0008268 |
– |
Данные автора |
|
CO2 |
30,48662 |
–4,092939 |
0,620806 |
–0,061011 |
0,0032451 |
–7,027E–5 |
[13] |
|
CH4 |
20,23303 |
–2,915760 |
0,371371 |
–0,024974 |
0,0006513 |
– |
[9] |
|
CH4 |
18,81124 |
–1,818667 |
0,136254 |
–0,005159 |
0,0000743 |
– |
[25] |
|
CO |
17,00663 |
–1,647067 |
0,122574 |
–0,004226 |
3,76328E–5 |
– |
[26] |
|
C2H6 |
20,71712 |
–2,397034 |
0,275367 |
–0,017105 |
0,0004143 |
– |
Данные автора |
|
C2H6 |
19,84650 |
–1,631380 |
0,115636 |
–0,004252 |
0,0000601 |
– |
[25] |
|
CH3N |
22,33125 |
–2,555513 |
0,291656 |
–0,018280 |
0,0004487 |
– |
Данные автора |
Примечания. Результаты работ пересчитаны в виде полиномов от x [9, 21]; зависимость от P, ГПа оценена согласно [22, (9)]; определения найдены исходя из плотности состояний (DOS), полученных при исследовании неупругого рассеяния нейтронов [24]; данные DFT-расчетов при 0 < P < 80 ГПa [6]; экспериментальные данные [26]; температурный интервал: 0 < T < 1000 °C [23]; 300 < T < 1200 °C [26]; 0 < T < 800 °C [25]. Прочерк – расчеты не проводились.
В интервале температуры 1000-1400 °C (вероятные условия образования алмаза в литосфере) факторы изотопного фракционирования, определенные по вычисленным значениям β, показаны на рис.1 в сравнении с ранее полученными результатами теоретических вычислений. Такие вычисления фракционирования изотопов азота в алмазе до сих пор основываются на β-факторах молекул, которые рассматриваются в качестве аналогов связей C-N в алмазе. В качестве аналога использовались молекулы HCN и CN– [9]. При 1127 °C Δ15N между молекулой HCN (алмазом) и флюидом составляет –2,3 (для NH3) и –1,1 ‰ (для N2). По результатам DFT-расчетов, изотопное фракционирование между алмазом и молекулой NH3 практически отсутствует (–0,01 ‰ при 1127 °C), а между алмазом и N2 при той же температуре –0,76 ‰. Отклонение результатов от –2,3 до –0,3 ‰. Уменьшение 15N/14N устанавливается в ряду соединений NH4+ > N2 > (алмаз, NH3) > CH3N > CN− > NH2. При температуре 1100 °C фракционирование между алмазом и указанными выше N-содержа-щими компонентами флюида оценивается в –2,23, –0,77, 0,01, 0,44, 1,31 и 2,85 ‰ и существенно (более чем на 1 ‰) выше оценки на основе связи C-N в алмазе по аналогии с молекулой CN–.
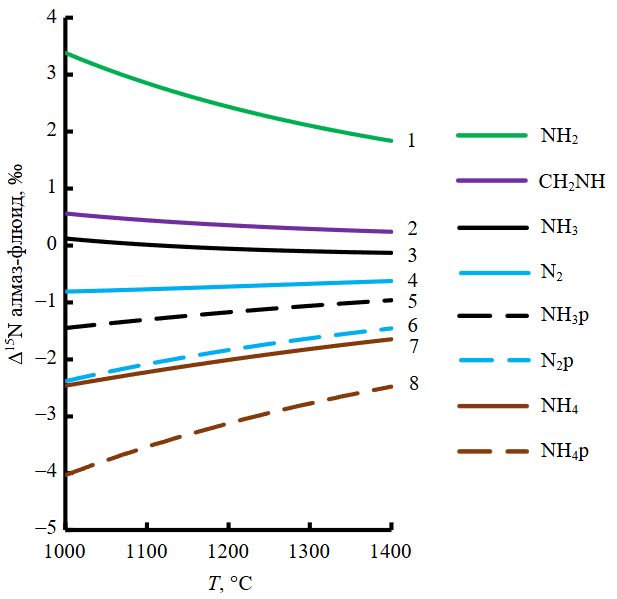
Рис.1. Изотопное фракционирование азота между алмазом и флюидом 1-4, 7 – факторы изотопного фракционирования, определенные методом DFT; 5, 6, 8 – оценки изотопного фракционирования при моделировании связи CN алмаза молекулой CN–
Значительные расхождения при замене связей азота в алмазе на молекулярные обуславли-ваются существенно различной силой и характером связей, что проявляется, например, в параметрах колебательных спектров. Фракционирование изотопов с конденсированными фазами отличается от фракционирования с газами того же состава [27], поэтому азот в алмазе может концентрировать тяжелый изотоп больше, чем молекулы газа HCN или CN−. Если в качестве модели фракционирования изотопов азота в алмазе принять молекулу CN–, то положительное значение Δ15N между алмазом и флюидом означает распространение в условиях верхней мантии таких N-содержащих соединений флюида, которые до сих пор не выявлены ни экспериментальными, ни теоретическими исследованиями. Таким образом, вычисленные β-факторы HCN и CN− молекул можно считать в лучшем случае лишь весьма грубыми приближениями для оценки изотопного фракционирования алмаза [9]. Для ряда соединений азота и углерода, которые могут быть специфичными для сублитосферной мантии, значения β-факторов уже известны (табл.1). Наши расчеты показывают, что азотные β-факторы NH2 существенно меньше, чем у других рассматриваемых молекул, так что даже при температуре, превышающей литосферные значения, происходит заметное обогащение алмаза изотопом 15N относительно равновесного флюида (около 2 ‰ при равновесном фракционировании алмаз-NH2, T = 1400 °C). Изотопное фракционирование углерода между алмазом и соединением C2H6 приблизительно соответствует фракционированию с CH4 (отличаясь на ≈ 0,2 ‰, T = 1400 °C). Эти соединения можно рассматривать в качестве возможных компонентов флюида при сублитосферном образовании алмаза.
Считается, что изотопное фракционирование азота между алмазом и флюидом при мантийных условиях существенно превышает изотопное фракционирование углерода с большинством известных углеродсодержащих алмазообразующих флюидов [21]. Наши результаты демонстрируют, что при температуре 1200 °C азотные β-факторы алмаза понижены относительно молекул N2 и NH4+ на 0,8 и 1,0 ‰, однако выше, чем β-факторы CH3N и особенно NH2 на 0,3 и 2,4 ‰. Фракционирование изотопов углерода между алмазом и молекулами флюида при этой же температуре увеличивается от отрицательных значений –3,5 (CO2), –1,8 (CO32–) и –0,4 ‰ (CH3N) до положительных 1,1 ‰ (CH4).
Эффект давления
Имеющиеся расчеты зависимости β-фактора от давления [22, 28] демонстрируют значимое (порядка 0, n ‰) увеличение β13С алмаза при T ≈ 1000-1200 °C и P > 10 ГПа. Методом DFT влияние давления можно определить по изменению β-факторов при вариации объема решетки (в рамках квазигармонического приближения – QHA), в том числе зависимости от объема V коэффициентов полиномов 1000 lnβ по x = 106/T2. При уменьшении объема алмаза V/V0 до 0,88 (что приблизительно соответствует давлению до 110 ГПа) полученные зависимости всех коэффициентов полинома линейные (r2 > 0,99):
Таким образом, справедливо разложение
Используя определение изотермического модуля объемной упругости KT = –V∂P/∂V и ограничиваясь членами второго порядка, соотношение (5) можно представить в виде
Для алмаза V0 = 3,416 см3; K = 442 ГПа, ∂K/∂P = 3,61 (наши результаты расчетов в рамках QHA, которые практически идентичны экспериментальным данным [29]: K = 445 ГПа при ∂K/∂P = 4). В целом изменение коэффициентов ai в зависимости от давления (табл.1) определяется выражением
При T= 1000 °C углеродный β-фактор увеличивается на 0,6 (при P = 10 ГПа), азотный – на 0,33 ‰. При T= 1700 °C изменение углеродного β-фактора составляет 0,25 (10 ГПа), азотного – 0,14 ‰. Таким образом, зависимость β-факторов от давления для изотопов азота приблизительно в два раза ниже, чем углерода. Для контроля можно воспользоваться данными по изменению постоянной решетки алмаза при замещении изотопов углерода. В частности, при T = 25 °C (∂β/∂P)T = 0,619 ГПа–1 и вычисленная величина изменения коэффициента теплового расширения α при изотопном замещении (Δα)/α = ΔV/3V = –(∂β/∂P)TRT/(3V) составляет 1,50E–4, что равно экспериментальному значению [23]. Полученные зависимости β13C или β15N алмаза от давления недостаточны для определения фракционирования изотопов между алмазом и флюидом, так как для флюидов высокой плотности оценка влияния P на β-факторы минералообразующих растворов все еще проблематична.
Рассмотренные β-факторы определяют величину фракционирования изотопов при образовании алмаза для объемных (валовых) свойств кристаллической решетки в условиях равновесия со средой роста. Величины β могут существенно (до нескольких промилле) понижаться в природных нанокристаллических алмазах (эффект размера). Например, на основе фононной плотности состояний (PDOS) по результатам неупругого рассеяния нейтронов и при разных размерах алмаза оценены изотопные сдвиги углеродных β-факторов 103 lnβbulk-103 lnβnano относительно валовых значений [24, рис.6]. Для наноалмазов изменение коэффициента Δa1 оценено по приблизительной оцифровке линий [24, рис.6], скорректированных на отклонение фононной DOS от параболического соотношения за счет поверхностных включений. Интерполяция значения Δa1 наноалмазов выражается линейной зависимостью от размера: Δa1 ≈ 1,7768 – 0,0092×размер, нм с коэффициентом детерминации r2 » 0,99. Изменение 1000 lnβ13С наноалмазов при 5 нм Δa1 – 1,799; при 40 нм Δa1 – 1,321; при 170 нм Δa1 – 0,227 ‰. При размере алмаза 5 нм сдвиги изотопных отношений за счет поверхностных эффектов могут достигать –1 ‰.
Возможна оценка поверхностных эффектов за счет преимущественного развития определенных граней роста алмаза и образования секториальной (в том числе изотопной) зональности [30]. Состав растущего кристалла является следствием конкуренции роста и диффузии у поверхности (например, GEM – модель ростового захвата [31]). Кристалл наследует состав поверхности роста при низкой диффузии у поверхности, что можно характеризовать числом Пекле:
где r – скорость роста, мм/с; L– толщина поверхностного слоя, нм; D – коэффициент диффузии рассматриваемого элемента (или изотопа). Грань роста представлена периодичной пластиной с количеством слоев LS. Внутренний слой определен структурой валового алмаза, внешние LS-1 слоев реконструированы [32]. Параметры вычисления CRYSTAL и наборы базисных векторов те же, что и при вычислении по объемной (валовой) структуре. Изменение 1000 lnβ относительно валовых значений приведенные в табл.1 значения.
Таблица 2
1000 lnβ граней роста алмаза
|
Индекс грани* |
LS |
a1 |
a2 |
a3 |
a4 |
a5 |
|
|
15N/14N |
|||||||
|
111 |
2 |
12,14579 |
–0,59010 |
0,03920 |
–0,00176 |
4,190E–5 |
|
|
|
4 |
12,93791 |
–0,60624 |
0,04139 |
–0,00204 |
4,621E–5 |
|
|
110 |
2 |
10,99022 |
–0,52717 |
0,02365 |
–0,00097 |
1,948E–5 |
|
|
|
4 |
12,70019 |
–0,69832 |
0,04544 |
–0,00304 |
3,966E–5 |
|
|
100 |
2 |
8,66005 |
–0,20426 |
0,01380 |
–0,00129 |
9,954E–7 |
|
|
|
4 |
11,30632 |
–0,41044 |
0,02322 |
–0,00102 |
2,129E–5 |
|
|
|
6 |
12,67306 |
–0,44731 |
0,02390 |
–0,00100 |
2,015E–5 |
|
|
13C/12C |
|
||||||
|
111 |
2 |
19,98622 |
–1,11557 |
0,08240 |
–0,00415 |
9,234E–5 |
|
|
|
4 |
20,50007 |
–1,17320 |
0,08803 |
–0,00447 |
9,997E–5 |
|
|
|
6 |
20,82774 |
–1,18265 |
0,08748 |
–0,00432 |
9,623E–5 |
|
|
110 |
2 |
18,23049 |
–0,93891 |
0,05031 |
–0,00205 |
4,197E–5 |
|
|
|
4 |
20,55262 |
–1,14874 |
0,08495 |
–0,00428 |
9,542E–5 |
|
|
100 |
2 |
14,19463 |
–0,44483 |
0,02006 |
–0,00074 |
1,364E–5 |
|
|
|
4 |
18,91818 |
–0,81383 |
0,04992 |
–0,00227 |
4,770E–5 |
|
|
|
6 |
20,02506 |
–0,85221 |
0,04975 |
–0,00216 |
4,402E–5 |
|
* Индекс Миллера.
Ключевые параметры модели можно контролировать при экспериментальных наблюдениях, но в природных условиях они в большинстве случаев не определены [32]. Поскольку объемные β-факторы характеризуют рост при равновесии (Pe << 1), то значения β-факторов для отдельных граней (табл.2) могут позволить оценить отклонение от идеальных условий.
Сравнение с природным фракционированием 15N/14N
В условиях изотопного равновесия между средой роста (однородным флюидом) и поверхностью образующегося алмаза (по механизму Рэлея), могут возникать линейные зависимости между отношениями 13C/12C, 15N/14N и логарифмом концентрации азота ln(N) которые отмечены в многочисленных работах [21, 33, 34]. Наблюдаемые ковариации как в пределах отдельных зерен алмаза, так и среди генетически связанных алмазов позволяют оценить «природное» изотопное фракционирование азота. Наклон линии регрессии между генетически связанными алмазами в координатах определяется равенством
где KN – коэффициент распределения азота между алмазом и флюидом; Δ = 1000 lnα, α – факторы равновесного изотопного фракционирования углерода 13C/12C или азота 15N/14N между поверхностью алмаза и средой роста [21]:
f – доля израсходованного флюида; fN – доля потребленных азотсодержащих соединений флюида. Если f = fC (доле потребленных при этом углеродсодержащих соединений флюида), то из приведенного соотношения следует
где δ13C0 или δ15N – изотопный состав алмаза на начальной стадии роста. Величина KN оценивается по зависимости δ13C от содержания азота в алмазе ln(N),
Применение приведенных выражений ограничивается флюидами с преобладанием углеродсодержащих соединений, но может быть обобщено и на флюиды смешанного состава. Например, приведены оценки фракционирования 15N/14N между алмазом и средами роста в –4,0 ‰ (при
T = 1100 °C для флюида с преобладанием карбонат-иона CO32–, Δ13C ≈ –1,7 ‰, KN = 4,4, кимберлит Джерихо [33]). Валовые данные по изотопному составу углерода и азота в алмазах из лерцолитового ксенолита, представляющего литосферную мантию, использованы для оценки значения Δ15N 1,2 ‰(T = 1200 °C, обогащенный метаном флюид [35]). Данные по сверхглубинным алмазам Гвинеи с температурой кристаллизации около 1725 °C применены для определения Δ15N между алмазом и флюидом (–4,5 ‰) в условиях кристаллизации из флюида с преобладанием CO32–, Δ13C = –0,9 ‰ [36].
Факторы изотопного фракционирования азота алмаза Δ15N, оцененные по природным ковариациям δ13C-δ15N-ln(N), зависят, помимо выбора величины Δ13C, от соотношения компонентов флюида и других параметров, в том числе от модели фракционирования и принятой температуры кристаллизации. Температуру кристаллизации оценивают по минеральным включениям в алмазе. Несмотря на многочисленные предположения и допущения, особенно при оценке величины KN, в отсутствие других калибровок данный способ до сих пор являлся практически единственной возможностью оценки Δ15N между алмазом и флюидом.
Можно сопоставить результаты определения Δ15N/Δ13C по ковариациям природных генетически связанных образцов с применением эмпирических зависимостей и факторов фракционирования, определенных в рамках настоящей работы. Из имеющегося массива данных [9, 37] выделяются 64 серии условно когенетичных алмазов, где наблюдается значимая корреляция Δ15N vs Δ13C (при доверительном интервале 1σ), по которым получено распределение отношения Δ15N/Δ13C (рис.2, сплошная красная линия). При доверительном интервале 2σ количество серий уменьша-ется (57 серий), однако существенных изменений в распределении не происходит (основной максимум Δ15/Δ13 около 0 и локальные максимумы около 1 и 2). Представительность каждой серии оценивалась с помощью t-распределения Стьюдента. Линиями показаны теоретические (см. табл.1) значения Δ15N/Δ13C между алмазом и флюидом разного состава, вычисленные при температуре 800-1800 оC. В числителе – состав соединения азота, в знаменателе – углерода. Сплошные линии – в предположении независимости фракционирования от KN = 1, пунктирные KN = 5, двойные пунктирные KN = 2,5. Двойная пунктирная зеленая линия – NH3/CO2, сплошные сиреневая – N2/CO2 и голубая – N2/CO3. При построении рисунка «эмпирические» факторы фракционирования, оцененные по природным соотношениям изотопов азота и углерода, не использованы. Большинство отношений Δ15N/Δ13C соответствуют значениям от –1,5 до 0,5 (с максимумом около –0,3). Близ-кие к нулю значения Δ15N/Δ13C могут обуславливаться преобладанием NH3 в качестве азотсо-держащей субстанции флюида при образовании алмаза (Δ15N близко к нулю) и/или доминирова-нием углеродсодержащего компонента с относительно большим фракционированием 13C/12C при образовании алмаза (CO2, CO3). Флюиды с преобладанием CO2+N2 или CO3+N2 характеризуются положительными отношениями Δ15N/Δ13C. В условиях двухкомпонентного источника углерода максимум распределения Δ15N/Δ13C может соответствовать изотопному обмену алмаза с CO2 или ионом карбоната в смеси с CH4 при доминировании N2 в качестве источника азота. Более высокие отношения Δ15N/Δ13C (локальные максимумы отношения Δ15N/Δ13C ≈ 1,5 и 2,3) соответствуют кристаллизации алмаза из флюида с доминированием NH4/CO2, N2/CO3 или NH2/CH4. В качестве источника возможны соединения C2H6 или CH3N. Отрицательные Δ15N/Δ13C соответствуют сочетанию таких компонентов, как NH4/CH4, N2/CH4 или NH3/CH4 (последнее при температуре выше 1250-1300 оC). Отметим, что с повышением температуры происходит сдвиг равновесных изотопных отношений 15N/13C. Эмпирически оцененные величины отношения Δ15N/Δ13C за пределами интервала от –4 до +4 могут свидетельствовать об экстремальных коэффициентах распределения азота между алмазом и средой роста или о присутствии каких-либо неучтенных компонентов флюида, обогащенных 15N или 13C относительно алмаза. В зависимости от соотношения Δ15N/Δ13C в когенетической серии алмазов при кристаллизации по механизму Рэлея может наблюдаться увеличение δ15N, уменьшение этого значения либо отсутствие какого-либо тренда.
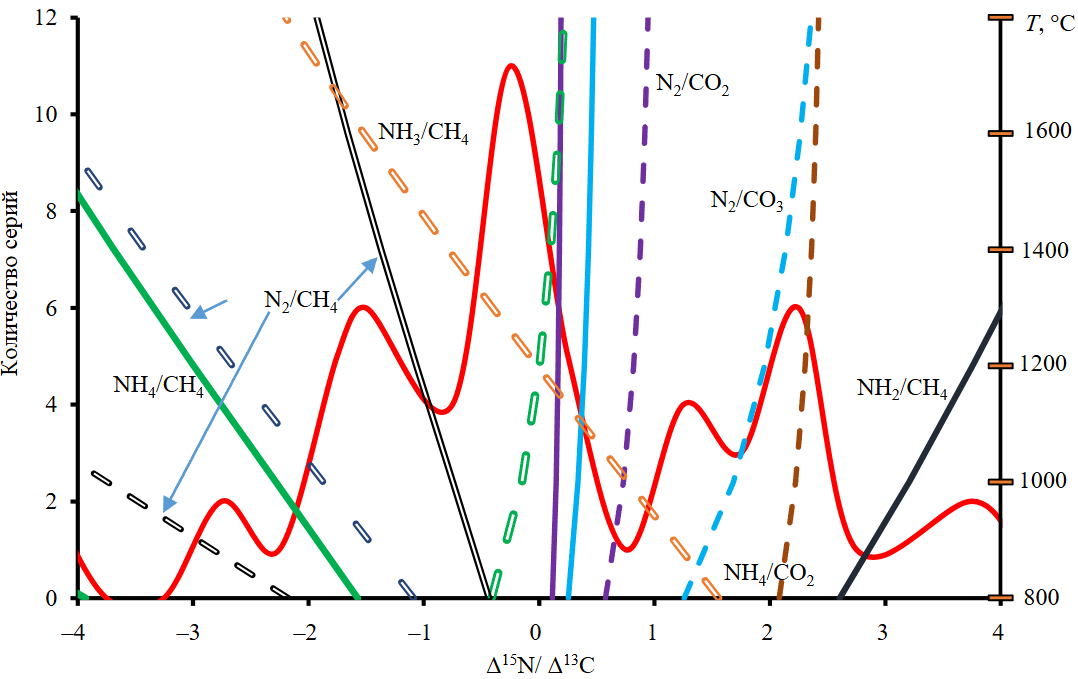
Рис.2. Частотное распределение значений отношения Δ15N/Δ13C по сериям анализов природных алмазов
Заключение
Факторы изотопного фракционирования углерода относительно хорошо известны для многих систем, относящихся к образованию алмаза. Распределение изотопов азота между алмазом и минералообразующим флюидом изучено гораздо меньше и в основном базируется на эмпирически наблюдаемых трендах среди природных алмазов, обуславливая существенные неопределенности оценок и необходимость более строгих определений [11]. Достоверные значения факторов фракционирования изотопов азота должны быть предпосылкой выяснения причин наблюдаемой изотопной неоднородности алмаза, природы ковариаций значений δ13C-δ15N-N, вещественного состава флюидов и других условий образования алмаза. Сделана попытка охарактеризовать фракционирование изотопов азота «из первых принципов» на основе кристаллохимических свойств алмаза с азотом замещения и азотсодержащими молекулами флюида.
В частности, методом «замороженных фононов» теории функционала плотности с использованием полноэлектронных базисов определены совокупности β-факторов (15N/14N, 13С/12С) алмаза в гармоническом и квазигармоническом приближениях при температурах от 0 до 2500 °C. Для достижения представительности при вычислениях применен метод расширенных ячеек (с увеличением объема в 8, 16, 27 раз). Определены значения некоторых β-факторов компонентов флюида (углеродных C2H6, CH3N и азотных CH3N) для расчета фракционирования изотопов при образовании алмаза. Результаты abinitio вычислений существенно отличаются от ранее полученных теоретических результатов, основанных на представлении CN-связей алмаза молекулярными соединениями HCN или CN–. В условиях образования алмаза при уменьшении объема под давлением факторы изотопного фракционирования азота и углерода могут увеличиваться на десятые доли промилле. Давление влияет на изотопное фракционирование азота алмаза больше, чем на фракционирование изотопов углерода, что при экстремальных условиях (суперхолодная субдукция) может приводить к увеличению факторов фракционирования до существенных значений. Увеличение объема решетки алмаза за счет теплового расширения частично компенсирует эффект давления, поэтому сдвиги изотопных отношений в целом определяются величиной градиента ΔP/ΔT. При «стандартных» литосферных условиях образования алмаза (около 6 ГПа и 1100 °C) изотопные факторы фракционирования углерода и азота меняются незначительно.
В зависимости от преобладающих субстанций азота и углерода фракционирование изотопов при образовании алмаза может приводить к различным зональности изотопного состава в пределах отдельных зерен и вариациям в пределах когенетических серий. В большинстве случаев (максимум распределения Δ15N/Δ13C на рис.2) фракционирование изотопов азота незначительно (Δ15N<<Δ13C), что согласуется с расчетами факторов фракционирования между алмазом и флюидом NH3-CO2 или N2-CO2. Сдвиги отношения Δ15N/Δ13C в область отрицательных значений могут свидетельствовать о восстановительных условиях при высоких давлениях и «холодной» геотерме [38]. В бедных азотом восстановленных мантийных флюидах [39] важную роль играют амины (NH2) и метанимин (CH3N), доминирование которых может соответствовать появлению локальных максимумов в распределении значений Δ15N/Δ13C. Окисленные флюиды с преобладанием CO2 или CO3 в сочетании с компонентом N2 характеризуются положительными отношениями Δ15N/Δ13C между алмазом и флюидом и существенно зависят от коэффициента распределения азота.
Литература
- Vasilev E., Zedgenizov D., Zamyatin D. et al. Cathodoluminescence of Diamond: Features of Visualization // Crystals. 2021. Vol. 11. Iss. 12. № 1522. DOI: 10.3390/cryst11121522
- Klepikov I.V., Vasilev E.A., Antonov A.V. Regeneration Growth as One of the Principal Stages of Diamond Crystallogenesis // Minerals. 2022. Vol. 12. Iss. 3. № 327. DOI: 10.3390/min12030327
- Губанов Н.В., Зедгенизов Д.А., Васильев Е.А., Наумов В.А. Новые данные о составе среды кристаллизации волокнистых алмазов из россыпей Западного Урала // Записки Горного института. 2023. Т. 263. С. 645-656.
- Zedgenizov D., Kagi H., Ohtani E. et al. Retrograde phases of former bridgmanite inclusions in superdeep diamonds // Lithos. 2020. Vol. 370-371. № 105659. DOI: 10.1016/j.lithos.2020.105659
- Пучков В.Н., Зедгенизов Д.А. Мантийная конвекция и алмазы // Литосфера. 2023. Т. 23. № 4. С. 476-490. DOI: 10.24930/1681-9004-2023-23-4-476-490
- Liu J., Wang W., Yang H. et al. Carbon isotopic signatures of super-deep diamonds mediated by iron redox chemistry // Geochemical Perspectives Letters. 2019. Vol. 10. P. 51-55. DOI: 10.7185/geochemlet.1915
- Cartigny P., Palot M., Thomassot E., Harris J.W. Diamond Formation: A Stable Isotope Perspective // Annual Review of Earth and Planetary Sciences. 2014. Vol. 42. P. 699-732. DOI: 10.1146/annurev-earth-042711-105259
- Cartigny P., Harris J.W., Javoy M. Diamond genesis, mantle fractionations and mantle nitrogen content: a study of δ13C–N concentrations in diamonds // Earth and Planetary Science Letters. 2001. Vol. 185. Iss. 1-2. P. 85-98. DOI: 10.1016/S0012-821X(00)00357-5
- Stachel T., Cartigny P., Chacko T., Pearson D.G. Carbon and Nitrogen in Mantle-Derived Diamonds // Reviews in Mineralogy and Geochemistry. 2022. Vol. 88. № 1. P. 809-875. DOI: 10.2138/rmg.2022.88.15
- Smit K.V., Timmerman S., Aulbach S. et al. Geochronology of Diamonds // Reviews in Mineralogy and Geochemistry. 2022. Vol. 88. № 1. P. 567-636. DOI: 10.2138/rmg.2022.88.11
- Cartigny P., Marty B. Nitrogen Isotopes and Mantle Geodynamics: The Emergence of Life and the Atmosphere–Crust–Mantle Connection // Elements. 2013. Vol. 9. № 5. P. 359-366. DOI: 10.2113/gselements.9.5.359
- Richet P., Bottinga Y., Javoy M. A Review of Hydrogen, Carbon, Nitrogen, Oxygen, Sulphur, and Chlorine Stable Isotope Fractionation Among Gaseous Molecules // Annual Review of Earth and Planetary Sciences. 1977. Vol. 5. P. 65-110. DOI: 10.1146/annurev.ea.05.050177.000433
- Polyakov V.B., Kharlashina N.N. The use of heat capacity data to calculate carbon isotope fractionation between graphite, diamond, and carbon dioxide: a new approach // Geochimica et Cosmochimica Acta. 1995. Vol. 59. Iss. 12. P. 2561-2572. DOI: 10.1016/0016-7037(95)00150-6
- Horita J. Carbon isotope exchange in the system CO2-CH4 at elevated temperatures // Geochimica et Cosmochimica Acta. 2001. Vol. 65. Iss. 12. P. 1907-1919. DOI: 10.1016/S0016-7037(01)00570-1
- Bigeleisen J., Mayer M.G. Calculation of Equilibrium Constants for Isotopic Exchange Reactions // The Journal of Chemical Physics. 1947. Vol. 15. № 5. P. 261-267. DOI: 10.1063/1.1746492
- Erba A., Desmarais J.K., Casassa S. et al. CRYSTAL23: A Program for Computational Solid State Physics and Chemistry // Journal of Chemical Theory and Computation. 2023. Vol. 19. Iss. 20. P. 6891-6932. DOI: 10.1021/acs.jctc.2c00958
- Yuting Zheng, Chengming Li, Jinlong Liu et al. Diamond with nitrogen: states, control, and applications // Functional Diamond. 2021. Vol. 1. № 1. P. 63-82. DOI: 10.1080/26941112.2021.1877021
- Palyanov Y.N., Borzdov Y.M., Khokhryakov A.F. et al. Effect of Nitrogen Impurity on Diamond Crystal Growth Processes // Crystal Growth & Design. 2010. Vol. 10. Iss. 7. P. 3169-3175. DOI: 10.1021/cg100322p
- Grimme S., Hansen A., Brandenburg J.G., Bannwarth C. Dispersion-Corrected Mean-Field Electronic Structure Methods // Chemical Reviews. 2016. Vol. 116. Iss. 9. P. 5105-5154. DOI: 10.1021/acs.chemrev.5b00533
- Schauble E.A., Young E.D. Mass Dependence of Equilibrium Oxygen Isotope Fractionation in Carbonate, Nitrate, Oxide, Perchlorate, Phosphate, Silicate, and Sulfate Minerals // Reviews in Mineralogy and Geochemistry. 2021. Vol. 86. № 1. P. 137-178. DOI: 10.2138/rmg.2021.86.04
- Petts D.C., Chacko T., Stachel T. et al. A nitrogen isotope fractionation factor between diamond and its parental fluid derived from detailed SIMS analysis of a gem diamond and theoretical calculations // Chemical Geology. 2015. Vol. 410. P. 188-200. DOI: 10.1016/j.chemgeo.2015.06.020
- Polyakov V.B., Kharlashina N.N., Shiryaev A.A. Thermodynamic properties of 13C-diamond // Diamond and Related Materials. 1997. Vol. 6. Iss. 1. P. 172-177. DOI: 10.1016/S0925-9635(96)00587-0
- Bottinga Y. Carbon isotope fractionation between graphite, diamond and carbon dioxide // Earth and Planetary Science Letters. 1968. Vol. 5. P. 301-307. DOI: 10.1016/S0012-821X(68)80056-1
- Shiryaev A.A., Polyakov V.B., Rols S. et al. Inelastic neutron scattering: a novel approach towards determination of equilibrium isotopic fractionation factors. Size effects on heat capacity and beta-factor of diamond // Physical Chemistry Chemical Physics. 2020. Vol. 22. Iss. 23. P. 13261-13270. DOI: 10.1039/d0cp02032j
- Polyakov V.B., Horita J. Equilibrium carbon isotope fractionation factors of hydrocarbons: Semi-empirical force-field method // Chemical Geology. 2021. Vol. 559. № 119948. DOI: 10.1016/j.chemgeo.2020.119948
- Kueter N., Schmidt M.W., Lilley M.D., Bernasconi S.M. Experimental determination of equilibrium CH4–CO2–CO carbon isotope fractionation factors (300-1200 °C) // Earth and Planetary Science Letters. 2019. Vol. 506. P. 64-75. DOI: 10.1016/j.epsl.2018.10.021
- Horita J., Wesolowski D.J. Liquid-vapor fractionation of oxygen and hydrogen isotopes of water from the freezing to the critical temperature // Geochimica et Cosmochimica Acta. 1994. Vol. 58. Iss. 16. P. 3425-3437. DOI: 10.1016/0016-7037(94)90096-5
- Поляков В.Б., Харлашина Н.Н. Влияние давления на фракционирование изотопов // Доклады Академии наук СССР. 1989. Т. 306. № 2. С. 390-395.
- Kunc K., Loa I., Syassen K. Equation of state and phonon frequency calculations of diamond at high pressures // Physical Review B. 2003. Vol. 68. Iss. 9. № 094107. DOI: 10.1103/PhysRevB.68.094107
- Reutsky V.N., Kowalski P.M., Palyanov Y.N. et al. Experimental and Theoretical Evidence for Surface-Induced Carbon and Nitrogen Fractionation during Diamond Crystallization at High Temperatures and High Pressures // Crystals. 2017. Vol. 7. Iss. 7. № 190. DOI: 10.3390/cryst7070190
- Watson E.B. A conceptual model for near-surface kinetic controls on the trace-element and stable isotope composition of abiogenic calcite crystals // Geochimica et Cosmochimica Acta. 2004. Vol. 68. Iss. 7. P. 1473-1488. DOI: 10.1016/j.gca.2003.10.003
- De La Pierre M., Bruno M., Manfredotti C. et al. The (100), (111) and (110) surfaces of diamond: an ab initio B3LYP study // Molecular Physics. 2014. Vol. 112. Iss. 7. P. 1030-1039. DOI: 10.1080/00268976.2013.829250
- Smart K.A., Chacko T., Stachel T. et al. Diamond growth from oxidized carbon sources beneath the Northern Slave Craton, Canada: A δ13C–N study of eclogite-hosted diamonds from the Jericho kimberlite // Geochimica et Cosmochimica Acta. 2011. Vol. 75. Iss. 20. P. 6027-6047. DOI: 10.1016/j.gca.2011.07.028
- Smit K.V., Stachel T., Luth R.W., Stern R.A. Evaluating mechanisms for eclogitic diamond growth: An example from Zimmi Neoproterozoic diamonds (West African craton) // Chemical Geology. 2019. Vol. 520. P. 21-32. DOI: 10.1016/j.chemgeo.2019.04.014
- Thomassot E., Cartigny P., Harris J.W., Viljoen K.S. Methane-related diamond crystallization in the Earth’s mantle: Stable isotope evidences from a single diamond-bearing xenolith // Earth and Planetary Science Letters. 2007. Vol. 257. Iss. 3-4. P. 362-371. DOI: 10.1016/j.epsl.2007.02.020
- Palot M., Pearson D.G., Stern R.A. et al. Isotopic constraints on the nature and circulation of deep mantle C–H–O–N fluids: Carbon and nitrogen systematics within ultra-deep diamonds from Kankan (Guinea) // Geochimica et Cosmochimica Acta. 2014. Vol. 139. P. 26-46. DOI: 10.1016/j.gca.2014.04.027
- Curtolo A., Novella D., Logvinova A. et al. Petrology and geochemistry of Canadian diamonds: An up-to-date review // Earth-Science Reviews. 2023. Vol. 246. № 104588. DOI: 10.1016/j.earscirev.2023.104588
- Yuan Li, Keppler H. Nitrogen speciation in mantle and crustal fluids // Geochimica et Cosmochimica Acta. 2014. Vol. 129. P. 13-32. DOI: 10.1016/j.gca.2013.12.031
- Сокол А.Г., Томиленко А.А., Бульбак Т.А. и др. Состав флюида восстановленной мантии по экспериментальным данным и результатам изучения флюидных включений в алмазах // Геология и геофизика. 2020. Т. 61. № 5-6. С. 810-825. DOI: 10.15372/GiG2020103
